基于Clamped B 樣條的空間非合作目標抓捕策略研究1)

王明明 羅建軍 余 敏

(西北工業(yè)大學深圳研究院,廣東深圳 518057)

(西北工業(yè)大學航天學院,西安 710072)

引言

空間機器人將在衛(wèi)星維修、在軌裝配、碎片清除等任務(wù)中發(fā)揮著重要作用.典型的在軌演示試驗如“Robot Technology Experiment(ROTEX)”、“Engineering Test Satellite VII(ETS-VII)”、“Orbital Express(OE)”和“鳳凰號”等項目驗證了空間機器人執(zhí)行在軌服務(wù)任務(wù)的可行性[1-4].然而,在軌服務(wù)任務(wù)最具挑戰(zhàn)性的工作之一是如何高效、可靠地抓捕目標衛(wèi)星.此外,空間機械臂與基座之間的動力學耦合引起的非完整約束對于抓取規(guī)劃提出了新的挑戰(zhàn).

過往文獻已提出多種空間機械臂軌跡規(guī)劃方法.增強干擾圖(EDM)的概念[5]首先被提出并應(yīng)用于空間機器人的啟發(fā)式軌跡規(guī)劃問題求解.然而,EDM很難計算,尤其是對于具有較高自由度的空間機械臂.此后,文獻[6]提出零反作用空間(RNS)的概念,被應(yīng)用于運動學非冗余和冗余空間機械臂的軌跡生成.文獻[7-8]考慮角動量守恒,使用RNS 的概念設(shè)計關(guān)節(jié)軌跡抓捕翻滾目標.然而,對于6 自由度機械臂而言,RNS 的體積十分有限.文獻[9]中,提出等效平衡臂和動態(tài)平衡控制(DBC)相結(jié)合的方案減少基座姿態(tài)干擾.文獻[10]提出了一種新的組合策略,將DBC 和RNS 集成到基于任務(wù)優(yōu)先級的求解框架中.此后,文獻[11]提出了空間雙臂機器人點到點零反作用操作的規(guī)劃策略.文獻[12]建模和分析了空間機器人系統(tǒng)的動力學耦合,并將動力學耦合應(yīng)用于最小化基座姿態(tài)干擾的運動軌跡規(guī)劃.此外,可采用不同的關(guān)節(jié)軌跡參數(shù)化方法,例如周期性均勻B 樣條[13]、Bezier 曲線[14]等;文獻[15]給出了一種笛卡爾軌跡參數(shù)化方法,使得自由漂浮空間機器人的軌跡規(guī)劃問題轉(zhuǎn)化為非線性優(yōu)化問題.非線性優(yōu)化問題可以采用遺傳算法、差分進化算法等進行求解.

以上研究主要是解決捕獲前階段空間機械臂的軌跡規(guī)劃問題,而未考慮抓捕目標后的任務(wù).通常,機械臂欲抓捕移動的目標,需要感知環(huán)境并生成適當?shù)淖ゲ恫呗?最終實現(xiàn)機械臂末端執(zhí)行器和目標抓捕點之間建立穩(wěn)固的連接.文獻[16]描述了一種在真實環(huán)境中工作的移動機械手的抓捕規(guī)劃方法,利用當前物體模型優(yōu)化機器人手的抓握位姿.文獻[17]提出了一種BiSpace 規(guī)劃算法,結(jié)合了雙向快速探索隨機樹(RRT)和RRT-JT 算法,通過同時探索多個空間來實現(xiàn)快速規(guī)劃.在此基礎(chǔ)上,文獻[18]提出了改進的RRT*與四次樣條曲線結(jié)合的協(xié)調(diào)路徑規(guī)劃方法.文獻[19]中提出了一種基于目標外形和操作任務(wù),學習人類抓取策略的抓捕集成方法.前期的抓捕規(guī)劃方法為在軌抓捕規(guī)劃提供了參考.通過在接近階段使用偏置動量方法,在接觸碰撞階段使用阻抗控制,以及在捕獲后階段進行分布式動量控制,文獻[20]提出了一種可行的控制序列,用于成功完成捕獲操作.文獻[21]基于視覺反饋,引入了一種引導(dǎo)操作機械臂先攔截,后消旋的非合作目標抓捕策略,形成了機器人捕獲具有未知漂移和翻滾目標的預(yù)測和規(guī)劃組合方案.考慮抓捕過程中碰撞引起機器人基座姿態(tài)變化的問題,文獻[22]提出一種碰撞前的機械臂構(gòu)型優(yōu)化方法.針對空間機械臂抓捕目標后的控制問題,文獻[23-24]設(shè)計了空間機器人在軌捕獲非合作目標的柔性機構(gòu),并分別基于神經(jīng)網(wǎng)絡(luò)的全階滑模避障柔順控制和動態(tài)緩沖柔順控制,實現(xiàn)抓捕過程的抗沖擊與彈性振動主動抑制,有效避免了機械臂關(guān)節(jié)電機的過載.文獻[25]設(shè)計了一類目標消旋策略并同時穩(wěn)定基座的協(xié)調(diào)控制方法.文獻[26]以三臂空間機器人為對象,提出一種基于位姿誤差反饋的軌跡規(guī)劃算法用于應(yīng)對奇異位形出現(xiàn)時的位姿誤差問題.文獻[27]系統(tǒng)地給出了空間雙臂機器人的協(xié)同測量及軌跡規(guī)劃方法.文獻[28]提出了空間雙臂機器人捕獲目標后輔助對接操作的協(xié)調(diào)控制方案.

前期研究在抓捕可行性和抓捕規(guī)劃方面存在以下缺點:(1)空間機器人抓捕策略未充分考慮目標的運動和機器人的抓捕能力,無法評估抓取可行性,并確定最佳抓捕時機;(2)非合作目標的抓捕規(guī)劃是一個多目標、多約束的非線性優(yōu)化問題,為評估抓捕規(guī)劃策略的有效性,在規(guī)劃過程中須充分考慮捕獲后的操作.如何實現(xiàn)對翻滾目標的安全可靠抓捕對開展后續(xù)的在軌服務(wù)任務(wù)至關(guān)重要.迄今為止,空間機械臂的抓取規(guī)劃仍然是一項極具挑戰(zhàn)性的工作.本文的目標是設(shè)計運動學冗余空間機械臂的抓捕規(guī)劃策略,同時充分考慮空間機械臂的抓捕能力、目標運動、關(guān)節(jié)限制和防碰撞等約束.選擇運動學冗余機械臂的原因在于其存在無窮多個逆運動學解,可用于滿足多約束條件,例如最小化基座姿態(tài)干擾、防碰撞、最大化力可操作度等.最終通過對抓捕策略的仿真驗證,為后續(xù)空間機器人抓捕動態(tài)非合作目標提供技術(shù)支撐.

1 動力學建模

1.1 空間機器人動力學

如圖1 所示,空間機器人系統(tǒng)由航天器基座與n個自由度的操作機械臂組成,共包括n+1 個對象.基于Lagrange 動力學方程,空間機器人系統(tǒng)的動力學方程可表示如下

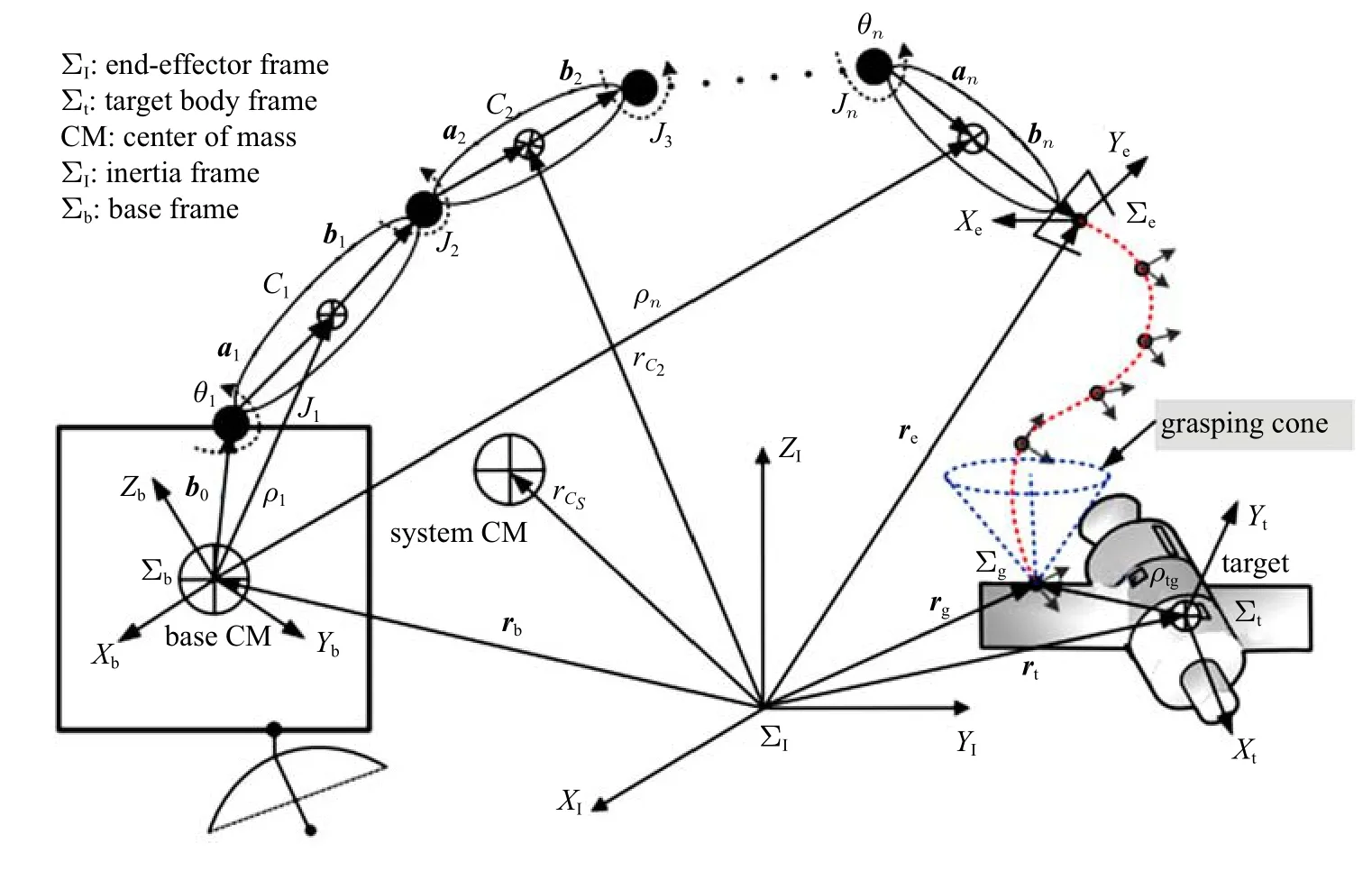
圖1 抓捕前空間機器人示意圖Fig.1 Schematic diagram of space robot in pre-capture phase

式中,Jg被稱為廣義雅可比矩陣[29].基于式(2)和式(3)可以看出,自由漂浮模式下基座和末端執(zhí)行器的運動僅依賴于關(guān)節(jié)軌跡及動力學耦合效應(yīng).因此,通過適當?shù)淖ゲ恫呗砸?guī)劃可實現(xiàn)多個優(yōu)化指標,如末端執(zhí)行器任務(wù),最小化基座干擾或最大化力可操作度等.

1.2 非合作目標動力學

圖2 抓捕后目標示意圖Fig.2 Schematic diagram of target in post-capture phase

如圖2 所示,目標衛(wèi)星的動力學可描述如下mt和It分別為目標衛(wèi)星的質(zhì)量和慣性張量.是單位矩陣.抓捕前階段,目標上的外力旋量ht=0,目標捕獲后,外力旋量ht=Gtehe,he∈R6.力旋量同時作用于末端執(zhí)行器,抓捕矩陣Gte 為

1.3 動靜態(tài)對偶性分析

根據(jù)虛功原理,作用于末端執(zhí)行器力旋量的虛功和關(guān)節(jié)力矩計算的虛功相等.參考式(1),末端執(zhí)行器力旋量與關(guān)節(jié)力矩間的關(guān)系可通過廣義雅可比矩陣的轉(zhuǎn)置來建立

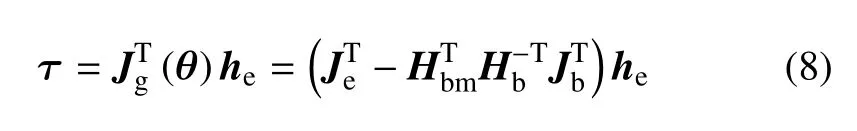
結(jié)合式(3)與式(8),可以給出動靜態(tài)對偶性的關(guān)系.目標一旦被捕獲,參考式(8)和ht=Gtehe,可以得出

下標?可以是e 或t;相應(yīng)地,⊙可以對應(yīng)設(shè)置為g 或c.從式(11)和式(12)可以看出,力可操作橢球的主軸與速度可操作橢球的主軸一致,而各軸的長度互為倒數(shù).根據(jù)動靜態(tài)對偶性分析,良好的力可操作性方向?qū)?yīng)較差的速度可操作性方向,反之亦然.這些特征將用于后續(xù)抓捕規(guī)劃策略設(shè)計中.

2 抓捕時機與可行性

一般而言,空間非合作目標上沒有固定的抓捕機構(gòu),因此,需要選擇星上特定的結(jié)構(gòu)作為可行的抓捕點.非合作目標上可以抓捕的位置包括:遠地點發(fā)動機邊緣、對接環(huán)、太陽能帆板支架等.為了輔助構(gòu)建空間機械臂的抓捕規(guī)劃策略,本文提出如下假設(shè):

(1)空間機器人系統(tǒng)和目標均為剛體,在執(zhí)行抓捕任務(wù)之前,空間機器人已通過軌道機動至相對于目標衛(wèi)星的某一固定位姿;

(2)空間機器人系統(tǒng)的初始角動量為0,抓捕過程中系統(tǒng)質(zhì)量特性不發(fā)生變化,目標的體坐標系處于目標質(zhì)心處;

(3)空間機器人系統(tǒng)的運動狀態(tài)和質(zhì)量特性已知,目標上的抓捕點事先已確定,并在抓捕點上附著有抓捕坐標系;

(4)抓捕過程中忽略環(huán)境力(重力梯度、地磁、太陽光壓等)以及相對軌道動力學效應(yīng).

2.1 抓捕能力圖譜

針對單一機械臂,其抓捕能力依賴于機械臂的運動學構(gòu)型、安裝位置等約束.為了完成對目標的抓捕和操作,機械臂需要更完備的抓捕能力描述.因此,結(jié)合機械臂的可達性和靈巧性概念[30],構(gòu)建機械臂的抓捕能力圖譜.

首先,目標上的抓捕點需要位于機械臂的工作空間WS之中,機械臂工作空間定義如下

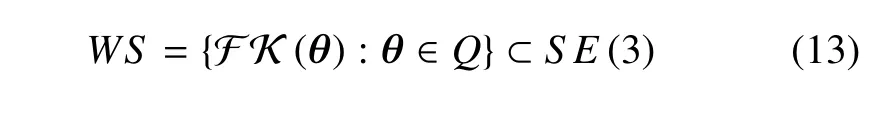
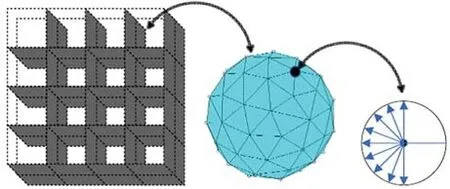
圖3 SE(3)離散化Fig.3 Discretization of SE(3)

其中,θ是機械臂的構(gòu)型空間,F K(θ)是正向運動學映射.機械臂的可達性圖譜描述了機器人工具中心點(TCP)坐標系能夠到達的所有可能位姿.如圖3所示,該圖譜的建立是通過在6 自由度空間中結(jié)構(gòu)化離散機械臂的工作空間完成的.首先,R3中的可達工作空間被分割成等體積的立方體單元,每個單元的姿態(tài)可達性通過單元內(nèi)接球上均勻分布空間點來實現(xiàn).可達性圖譜可存儲為二進制矩陣,每個塊的值代表TCP 局部區(qū)域的可達性,值為1 表示可達,為0 表示末端執(zhí)行器不可達.可達性圖譜的計算可以基于機械臂的逆運動學.本文中,工作空間離散為nv個立方體單元,每個內(nèi)接球上平均分布了nd個點,每個內(nèi)接球上的點進行了nz次旋轉(zhuǎn).

靈巧性為機械臂的操作能力提供了更為豐富的信息,每個立方體單元的靈巧性指標可以定義如下

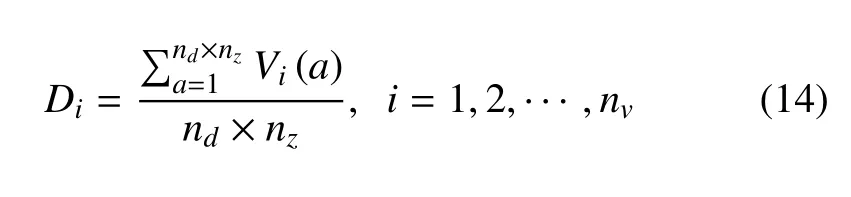
Vi(a)表示可達性圖譜中第i個立方體單元的二進制值.Di有效地給出了每個立方體單元中不同位姿的可達概率并給出了其靈巧性評估.結(jié)合可達性與靈巧性,將每個立方體單元的靈巧性值用相應(yīng)的顏色表征,可以構(gòu)建機械臂的抓捕能力圖譜,如圖4 所示.抓捕能力圖譜給出了機械臂工作空間中可以靈巧操作目標的程度,結(jié)合目標的運動預(yù)測,可以確定抓捕時間窗口并評估抓捕的可行性.

2.2 抓捕時機確定

以往的研究未充分考慮抓捕過程中機械臂的抓捕能力、目標的運動、末端執(zhí)行器的接近方向等問題,如圖5 所示,抓捕時機確定依賴于機械臂的抓捕能力分析、初始構(gòu)型、抓捕坐標系以及目標的運動預(yù)測.首先,基于工作空間WS分析,確定抓捕時間窗口;此后,給定目標的初始運動條件,搜索最優(yōu)的未來時刻,保證目標上的抓捕點位于能力圖譜內(nèi)且具有更高的靈活性指標,此外,末端執(zhí)行器與抓捕點的距離要盡可能小,位置矢量ρeg=rg(t)?和抓捕坐標系矢量nx之間的夾角亦需盡可能小,從而保證接近方向處于接近走廊內(nèi).因此,抓捕時機確定問題可描述如下

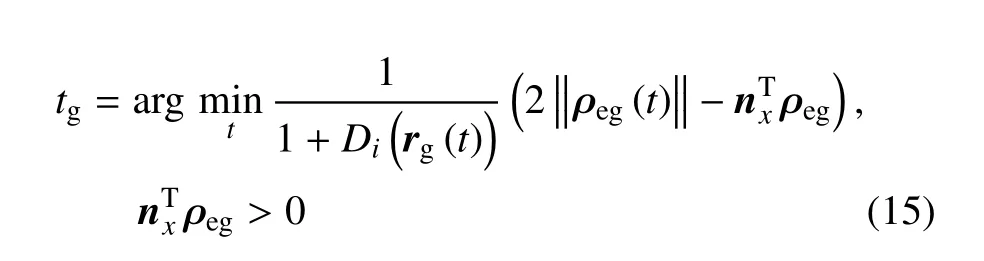
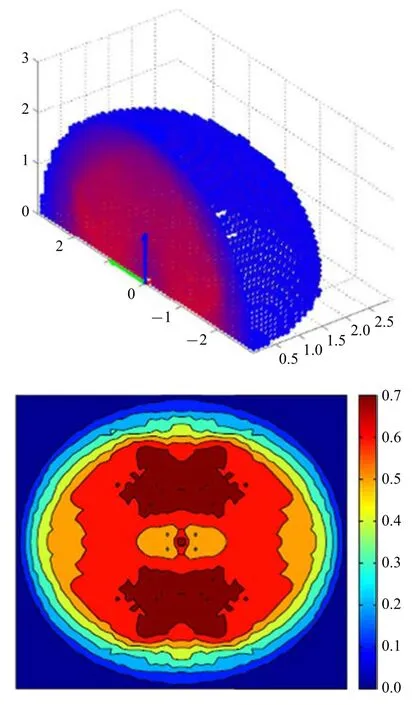
圖4 抓捕能力圖譜及切面等高線圖Fig.4 Capability map and section contour map

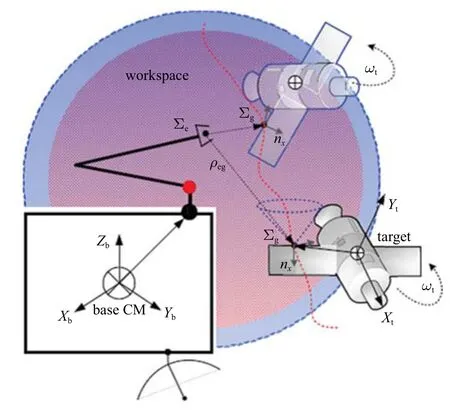
圖5 抓捕時機確定示意圖Fig.5 Schematic diagram of determining optimal grasping time

其中,Dirg(t)是抓捕點在工作空間WS的靈巧性指標,nx是旋轉(zhuǎn)矩陣Rg(t)的第一列.給定初始狀態(tài),rg(t)和Rg(t)的計算可以根據(jù)式(4)得到.

3 抓捕規(guī)劃器設(shè)計

3.1 問題描述

空間機械臂的抓捕規(guī)劃與控制受到動力學耦合的影響,自由漂浮模式下由于非完整約束的存在,機械臂各關(guān)節(jié)的構(gòu)型是路徑依賴的.抓取規(guī)劃策略的目標是確定最優(yōu)的抓捕時機并生成可行的,不違反各類約束的關(guān)節(jié)運動軌跡θ(t).一般而言,抓捕策略可描述為不等式約束gi(θ)與等式約束hi(θ)下的非凸優(yōu)化問題:

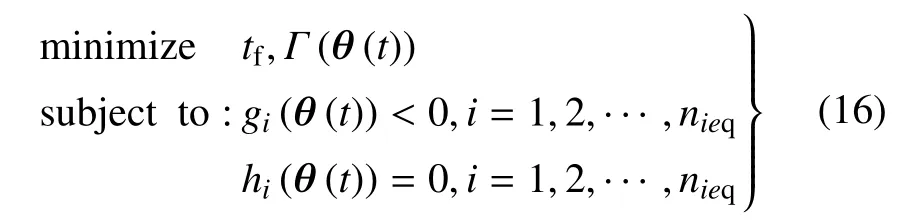
3.2 約束與目標函數(shù)

抓捕規(guī)劃中的約束可以分為等式約束與不等式約束.運動狀態(tài)x帶有上標s,f,d 分別表示初始、終端和期望的位姿.等式約束主要用于描述關(guān)節(jié)的初始位置、初始速度和初始加速度

同樣地,抓捕規(guī)劃的不等式約束可列寫如下.

(1)關(guān)節(jié)限幅:抓捕過程中需要考慮關(guān)節(jié)的運動能力,保證各關(guān)節(jié)不超出其運動范圍

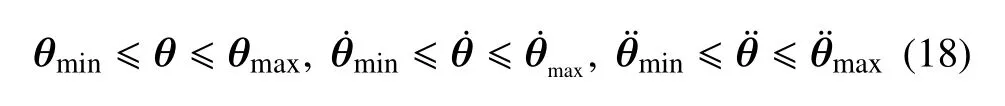
(2)抓捕走廊:參考圖1,末端執(zhí)行器的接近方向必須限制在一個抓捕走廊內(nèi)

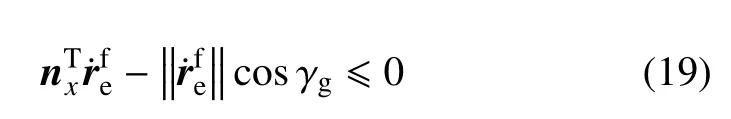
(3)碰撞規(guī)避:抓捕過程中需要保證機械臂與目標之間、各關(guān)節(jié)之間不發(fā)生碰撞

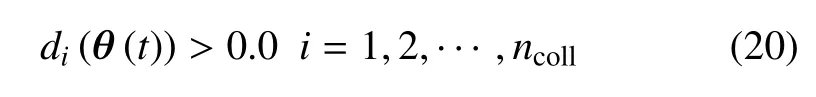
由于自由漂浮空間機器人非完整約束的存在,航天器基座和末端執(zhí)行器的終端狀態(tài)不僅依賴于逆運動學,也依賴于動力學耦合效應(yīng).假定和xb=(rb,qb)分別表示末端執(zhí)行器和基座的位姿,姿態(tài)描述采用四元數(shù)q={η,ε} ∈R4表示,相對四元數(shù)的計算公式如下

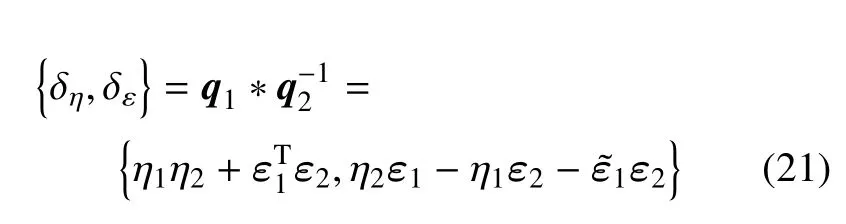
δε=0 表示兩個旋轉(zhuǎn)坐標系重合.基于單位四元數(shù),并考慮式(2)和式(3),基座與末端執(zhí)行器的終端位姿計算如下

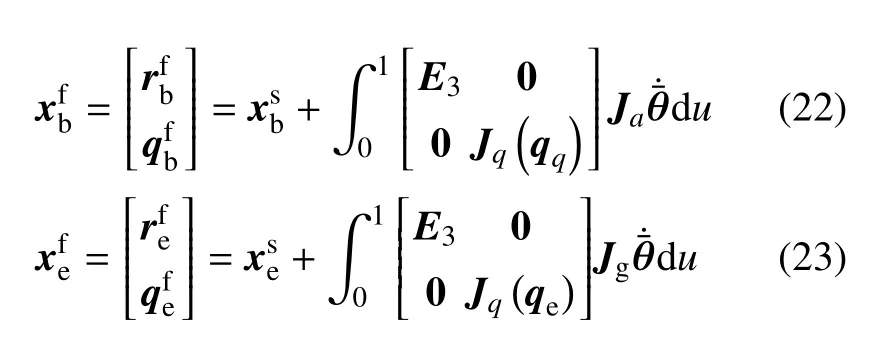
Jq=通過應(yīng)用正向運動學,避免了動力學奇異的發(fā)生.終端位姿與期望位姿的偏差可計算如下

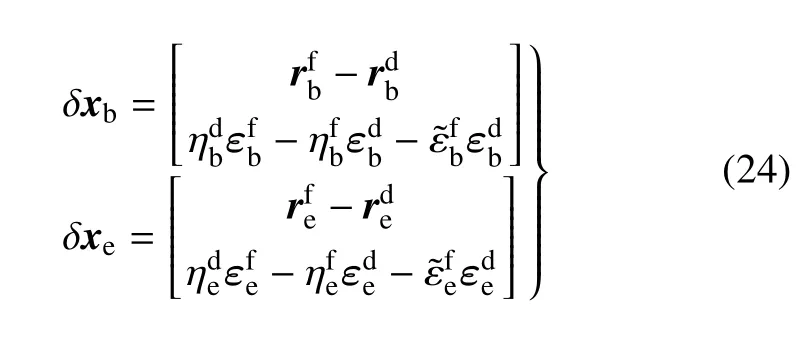
基于上述分析,空間機械臂抓捕規(guī)劃策略考慮如下的優(yōu)化指標.

(1)調(diào)整末端執(zhí)行器狀態(tài):抓取規(guī)劃要求機械臂末端執(zhí)行器的終端位姿、速度要盡可能的與目標上的抓捕點相匹配.因此,定義如下的優(yōu)化指標

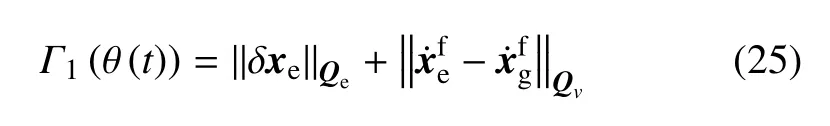
(2)最小化基座干擾:為保持通信、觀測等要求,期望在抓捕過程中最小化基座干擾.因此,定義如下的優(yōu)化指標

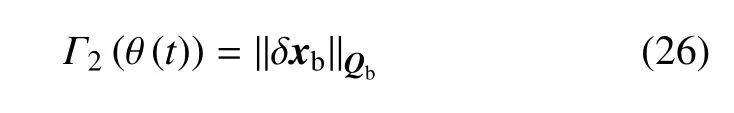
(3)最大化力可操作度:抓取完成后,需要對目標進行消旋、調(diào)姿等操作,因此,需要最大化抓捕后的力可操作度

3.3 關(guān)節(jié)參數(shù)化

為保證抓取過程中關(guān)節(jié)位置、速度、加速度的連續(xù)性,參考文獻[14],各關(guān)節(jié)的軌跡θi(t)可以參數(shù)化為多項式曲線,如Bezier 曲線,正弦多項式曲線等.本文中,采用B 樣條對關(guān)節(jié)進行參數(shù)化.B 樣條相比于Bezier 曲線的構(gòu)建需要更多的信息,但是它具備如下優(yōu)點:首先,B 樣條曲線是一類Bezier 曲線;其次,B 樣條曲線具備Bezier 曲線的所有特性;再次,B 樣條曲線相比Bezier 曲線提供了更好的控制靈活性.B樣條曲線的階次與其控制點的個數(shù)無關(guān),亦即,可采用低階曲線和更多控制點來構(gòu)建運動曲線.此外,B樣條曲線具有局部修正特性,改變某一個控制點并不會全局的改變曲線的形狀,此特性對于非線性優(yōu)化過程中的求解十分有利.

給定d+1 個控制點Pi,0,Pi,1,···,Pi,d和有m+1 個節(jié)點的節(jié)點矢量U={u0,u1,···,um},u0≤u1≤··· ≤um,對于p階次的Clamped B 樣條,首節(jié)點與末節(jié)點具有重復(fù)度p+1,因此,對應(yīng)于m+1 個節(jié)點的節(jié)點矢量,u0=u1=···=up=0 和um?p=um?p+1=···=um=0.關(guān)節(jié)軌跡θi(t)可以描述為歸一化的Clamped B 樣條曲線

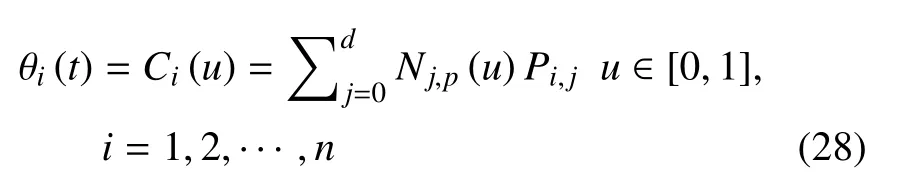
其中Nj,p是B 樣條的基函數(shù),可以遞歸計算如下

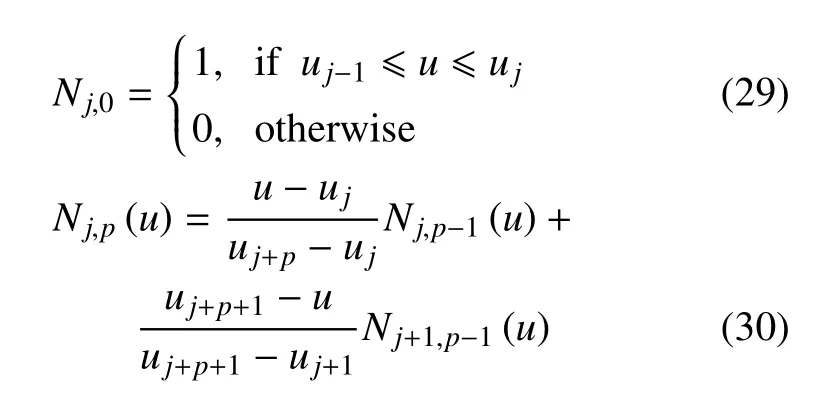
上式通常被稱為Cox-de Boor 遞歸公式.值得注意的是d,m和p滿足m=d+p+1.由于u是歸一化時間,對于軌跡的執(zhí)行時間T=tf?ts,如果定義t=u·T,關(guān)節(jié)速度和加速度可以計算如下

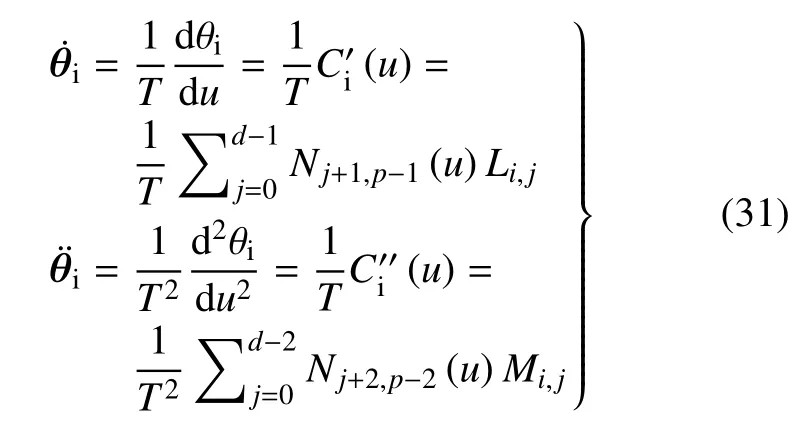
式中

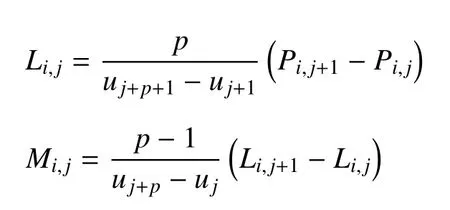
本文中,選擇四次Clamped B 樣條曲線p=4,d=7,m=12 對關(guān)節(jié)軌跡進行參數(shù)化.B 樣條曲線的基函數(shù)計算可參考圖6.式(18)中關(guān)節(jié)速度和加速度約束可通過調(diào)整執(zhí)行時間滿足

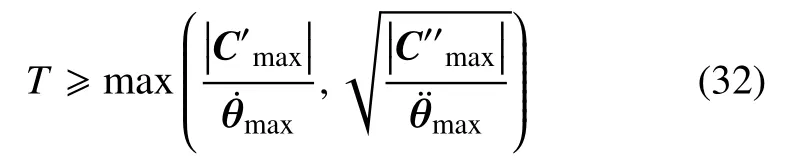
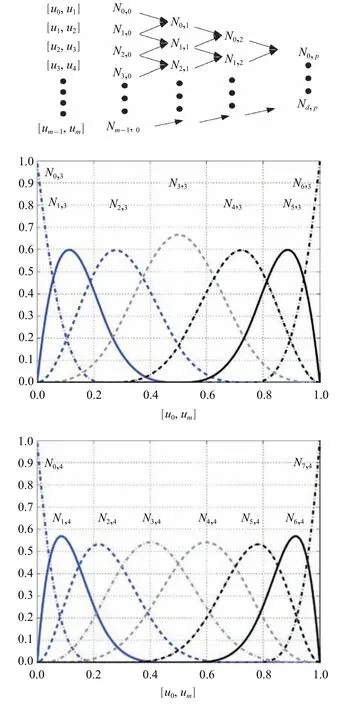
圖6 B 樣條基函數(shù)計算Fig.6 B spline basic functions calculation

其中,C′=dθ/du且C′′=d2θ/du2.tg?ts≥T意味著軌跡執(zhí)行時間足夠長且滿足式(18),終端時間可以設(shè)定為tf=tg;否則,需要更新Pi,j重新構(gòu)建關(guān)節(jié)軌跡.將式(17)中的等式約束代入式(28)和式(31)可得Pi,0=Pi,1=Pi,2=.由于已知,描述關(guān)節(jié)軌跡的Clamped B 樣條曲線形狀僅依賴于剩余的控制點Pi,3,Pi,4,···,Pi,d.考慮到空間機械臂的n個關(guān)節(jié),定義p=[P1,3,P1,4,···,P1,d,P2,3,P2,4,···,Pn,3,Pn,4,···,Pn,d]T作為設(shè)計變量,一旦p確定,即可確定每個關(guān)節(jié)的軌跡,進而得到抓捕規(guī)劃策略.因此,式(16)中的抓捕規(guī)劃問題可轉(zhuǎn)化為如下的優(yōu)化問題

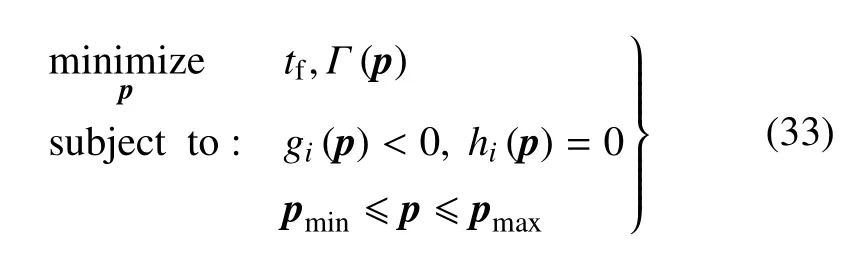
上述問題將利用自適應(yīng)慣性權(quán)重的粒子群優(yōu)化算法(PSO)進行求解,算法基本步驟如下:首先在可行的搜索區(qū)域內(nèi)初始化具有隨機初始值的粒子群.單個粒子維度即為設(shè)計變量的維數(shù).然后,各粒子對其適應(yīng)度函數(shù)進行評估,在搜索空間內(nèi)搜索目前已知的自身最佳粒子(局部)和整群中的最佳粒子(全局).各粒子的運動由局部及全局最佳粒子指導(dǎo),每一代更新一次.當發(fā)現(xiàn)更好的粒子時,就選作新一代粒子群運動的指導(dǎo)粒子.此過程不斷重復(fù),直到滿足特定收斂條件或發(fā)現(xiàn)有更好的解決方案.PSO 算法執(zhí)行過程中,需要考慮如何處理約束及選擇合適的適應(yīng)度函數(shù),參考文獻[31-32],采用修復(fù)不可行解集的方法處理本文中的不等式約束違反;適應(yīng)度函數(shù)選取式(25)用于評估每個粒子的優(yōu)劣,并存儲可行的空間機械臂抓捕規(guī)劃解集,而后基于式(26)和式(27)進行多目標優(yōu)化解集的選取與確定.

4 仿真結(jié)果

為驗證本文提出的抓捕規(guī)劃策略,本節(jié)給出了抓捕翻滾目標的仿真驗證.空間機器人系統(tǒng)由一個7 DOF 運動學冗余機械臂和6 DOF 航天器組成,運動學和動力學參數(shù)在表1 中給出,其中ai,bi和Ii在各運動體的體坐標系中進行描述.在抓捕過程中,首先基于機械臂的抓捕能力圖譜、初始構(gòu)型、目標運動預(yù)測等信息確定最優(yōu)抓捕時機tg.此后利用PSO 算法搜索求解式(33),構(gòu)建基于Clamped B 樣條的關(guān)節(jié)軌跡,生成空間機械臂的抓捕規(guī)劃策略.

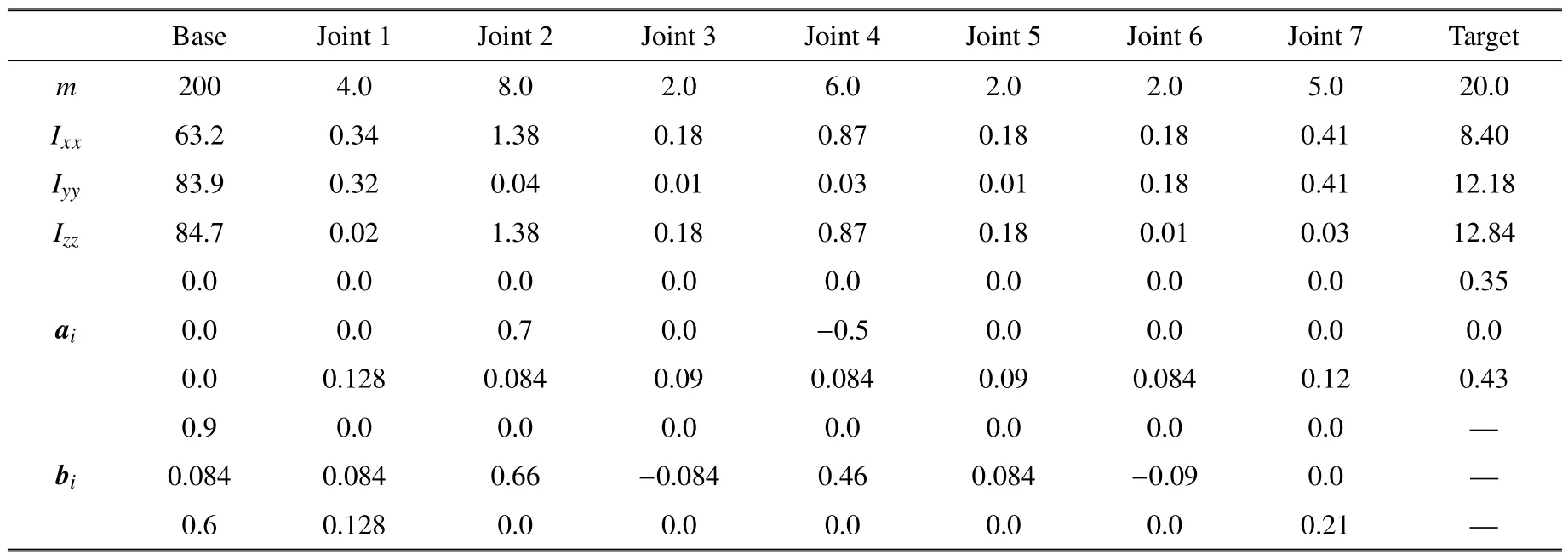
表1 空間機器人運動學與動力學參數(shù)Table 1 Kinematic and dynamic parameters of space robot

基于PSO 的求解結(jié)果,共選擇三組記錄來評價非合作目標抓捕規(guī)劃策略.三組記錄對應(yīng)的解集可參見表2.針對式(26)和式(27),不同優(yōu)化指標所構(gòu)成的Pareto 前沿如圖7 所示.圖8～圖10 給出了三組不同解集對應(yīng)的關(guān)節(jié)軌跡、末端執(zhí)行器與基座的運動情形.可以看出,所有解集均滿足仿真設(shè)定的終端狀態(tài)誤差要求.此外,抓捕過程中保證了空間機器人系統(tǒng)的動量守恒.在終端抓捕時刻,對于Test 1,最終的力可操作度為0.818,總的基座姿態(tài)干擾為0.630;對于Test 2,最終的力可操作度為0.588,總的基座姿態(tài)干擾為0.083;對于Test 3,最終的力可操作度為0.736,總的基座姿態(tài)干擾為0.271.可以看出,末端執(zhí)行器最終實現(xiàn)了對目標上抓捕點位姿和速度的匹配,同時最小化基座姿態(tài)干擾和最大化末端執(zhí)行器力可操作度兩個優(yōu)化指標均有考慮,而選擇不同的優(yōu)化指標最終將影響空間機器人系統(tǒng)的終端狀態(tài).

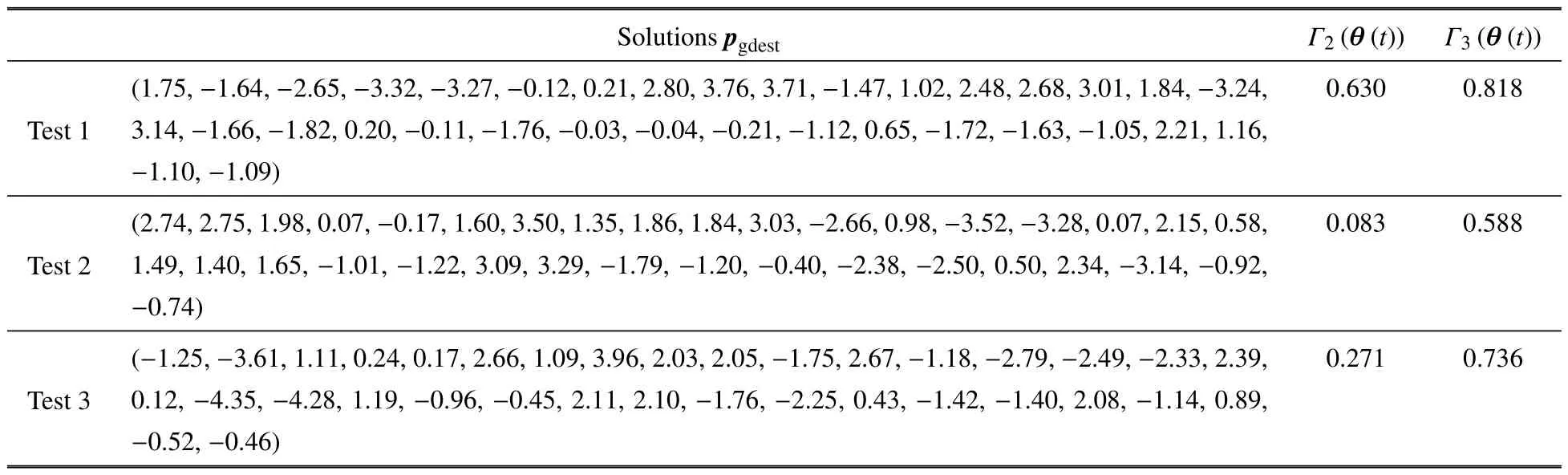
表2 針對不同優(yōu)化指標的解集Table 2 Optimal solutions to different objectives

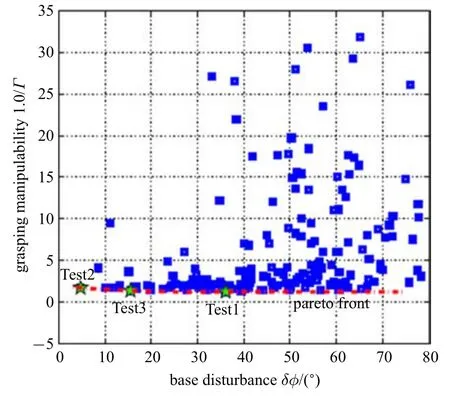
圖7 Pareto 前沿Fig.7 Pareto front

5 結(jié)論

空間機器人抓捕規(guī)劃過程中,需要考慮非合作目標的運動和機械臂的抓捕能力;此外,充分利用機械臂與基座間的動力學耦合特性,可有效提高空間機器人系統(tǒng)的燃料利用率,論文的主要工作列寫如下:

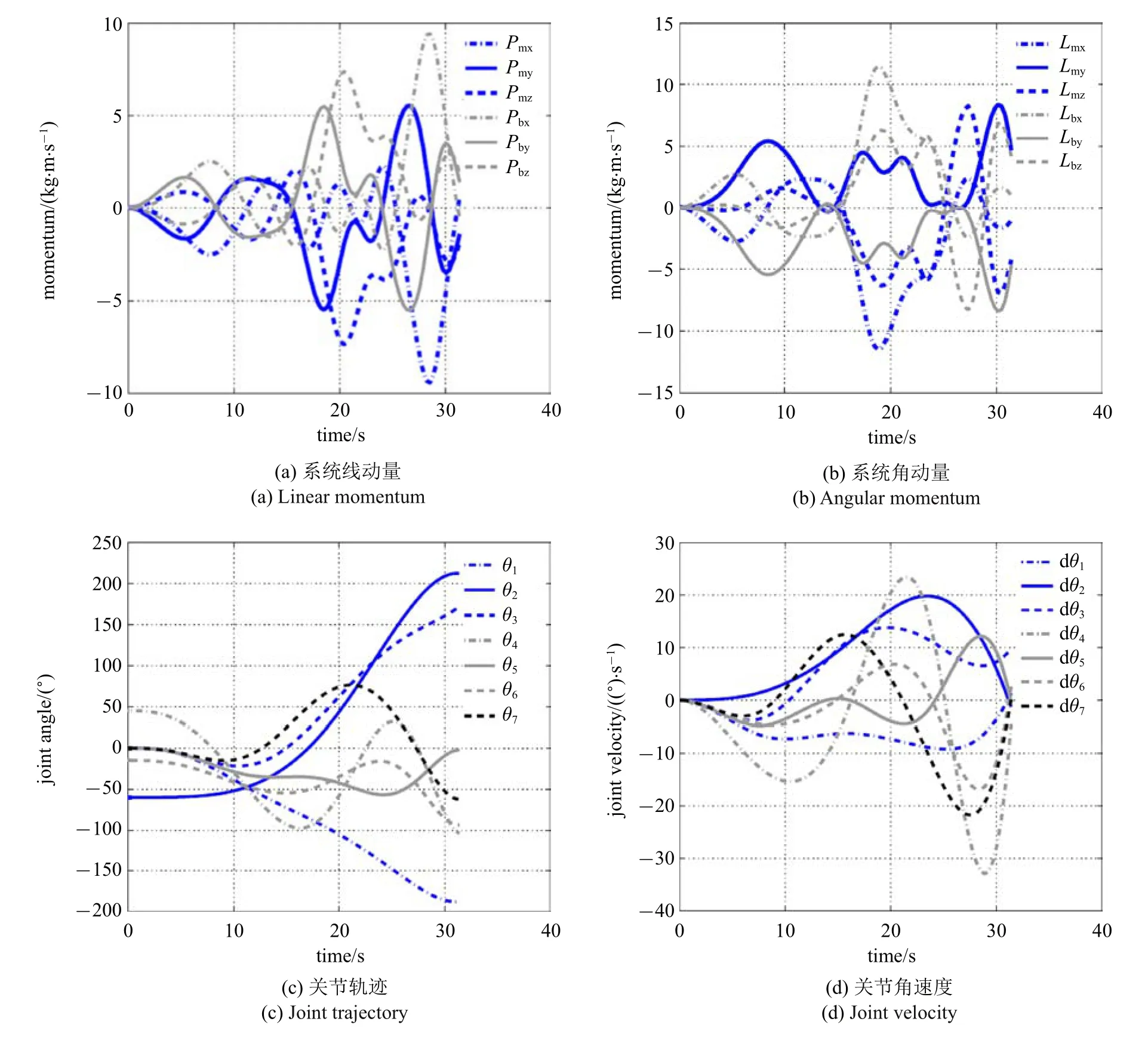
圖8 Test1 對應(yīng)的關(guān)節(jié)軌跡、基座與末端執(zhí)行器狀態(tài)Fig.8 Joint trajectories,base and end-effector’s states for Test1

圖8 Test1 對應(yīng)的關(guān)節(jié)軌跡、基座與末端執(zhí)行器狀態(tài)(續(xù))Fig.8 Joint trajectories,base and end-effector’s states for Test1(continued)

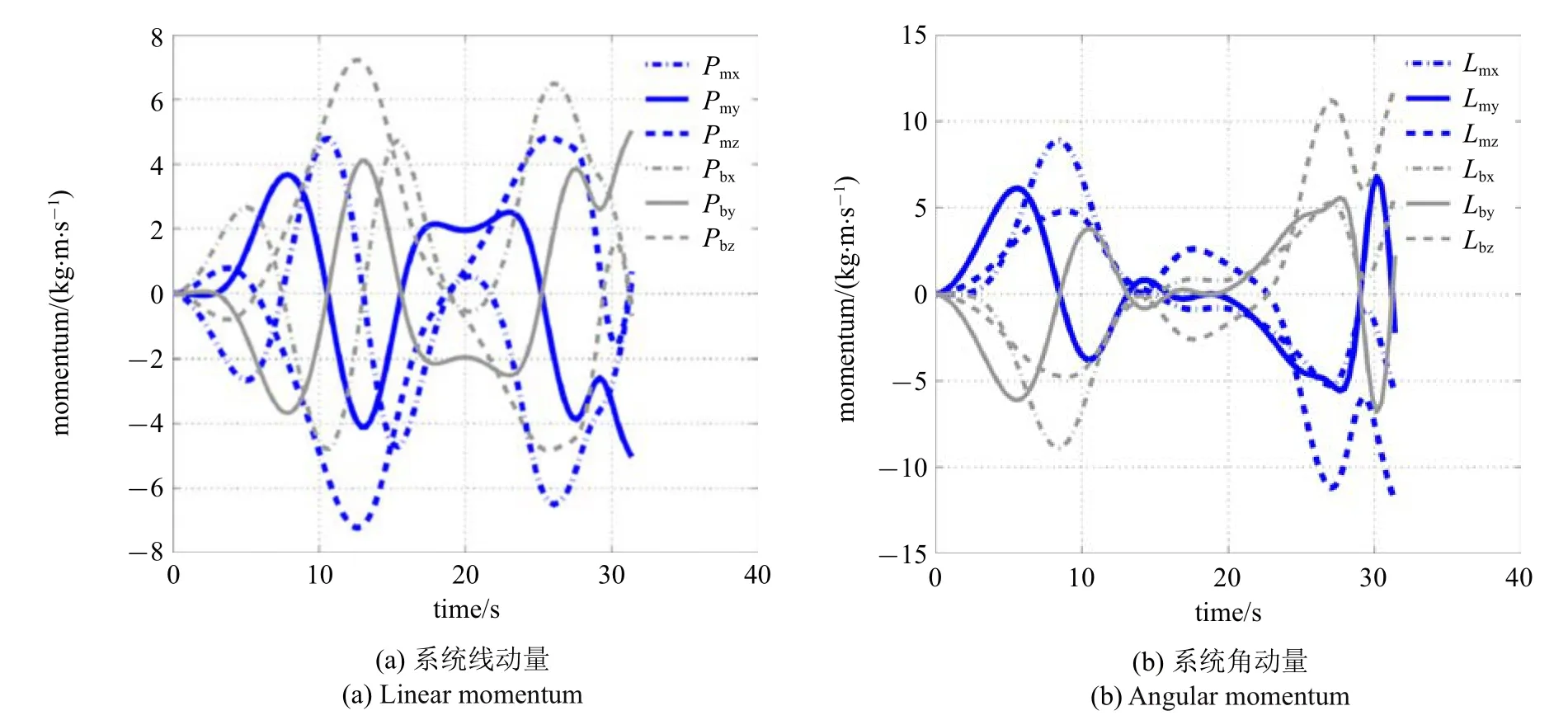
圖9 Test2 對應(yīng)的關(guān)節(jié)軌跡、基座與末端執(zhí)行器狀態(tài)Fig.9 Joint trajectories,base and end-effector’s states for Test2

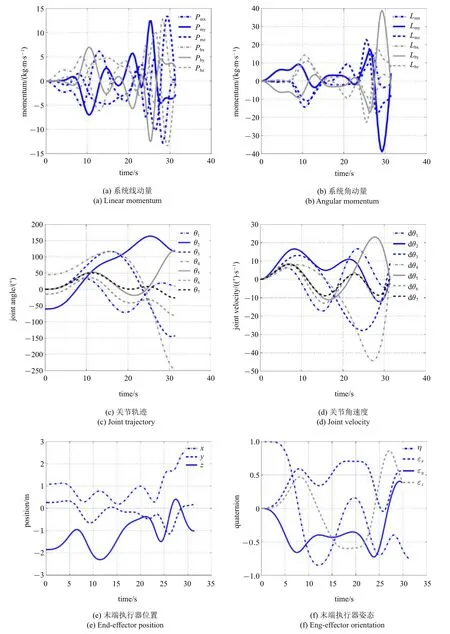
圖10 Test3 對應(yīng)的關(guān)節(jié)軌跡、基座與末端執(zhí)行器狀態(tài)Fig.10 Joint trajectories,base and end-effector’s states for Test3

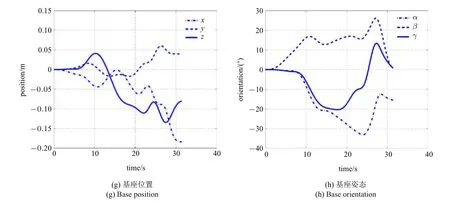
圖10 Test3 對應(yīng)的關(guān)節(jié)軌跡、基座與末端執(zhí)行器狀態(tài)(續(xù))Fig.10 Joint trajectories,base and end-effector’s states for Test3(continued)

(1)考慮機械臂抓捕能力、目標運動、末端執(zhí)行器接近方向及TCP 與抓捕點相對距離等因素,確定了空間機械臂的最優(yōu)抓捕時機,并給出了抓捕點在抓捕時刻的終端位姿和速度;

(2)考慮自由漂浮空間機器人的非完整約束,末端執(zhí)行器的運動不僅依賴于逆運動學,也依賴于歷史運動路徑.由于本文所提方法無需對Jacobian 矩陣求逆,運動學與動力學奇異均得到了規(guī)避;

(3)采用Clamped B 樣條曲線對機械臂關(guān)節(jié)的軌跡進行參數(shù)化,并對末端執(zhí)行器的終端狀態(tài)進行了優(yōu)化;此外,將最小化基座干擾和最大化力可操作度作為抓捕后的優(yōu)化指標.

仿真結(jié)果驗證了所提算法可應(yīng)用于抓捕時機的快速確定并生成優(yōu)化的抓捕關(guān)節(jié)軌跡,算法可有效擴展其應(yīng)用于多臂機器人在軌抓捕過程之中.具有測量和參數(shù)不確定性的魯棒協(xié)調(diào)控制在本文中未充分考慮,將是論文的未來工作之一.