基坑分段開挖下部盾構(gòu)隧道縱向變形規(guī)律研究

安偉博

(中鐵工程設(shè)計咨詢集團有限公司濟南設(shè)計院，濟南 250022)

隨著我國地鐵大規(guī)模建設(shè)和城市化進程加速，上跨既有盾構(gòu)隧道的基坑工程越來越多[1-2]。對工程措施和下部盾構(gòu)隧道變形規(guī)律進行研究尤為重要。

已有許多學(xué)者進行相關(guān)研究，陳郁通過用Mindlin彈性半空間應(yīng)力解和彈性地基梁理論得出隧道隆起的定量計算公式[3]；歐雪峰利用Mindlin解和Pasternak雙參數(shù)地基模型，得出考慮降水時隧道的隆沉變形規(guī)律[4]；黃栩認(rèn)為在計算隧道縱向變形時，Kerr地基模型最為精確，Pasternak模型次之，Winkler模型的計算結(jié)果最不理想的結(jié)論[5]。然而，理論方法多適用單次簡單開挖，很難對復(fù)雜多次分段開挖問題進行計算和假定分析，局限性很大。

孫波等通過Plaxis軟件對上跨、臨近隧道或車站基坑工程的開挖模擬，認(rèn)為合理選擇基坑開挖順序、減少基坑單次暴露長度對控制隧道和車站變形具有重要作用[6]；汪鵬程等通過Flac3d等軟件模擬了上跨盾構(gòu)隧道基坑開挖過程，認(rèn)為坑底加固、抽條放坡開挖+板錨支護、分段開挖+“板凳樁”加固對減小隧道隆起變形效果明顯；魏綱等通過對臨近和上跨隧道的基坑工程的實際監(jiān)測，得出隧道橫截面變形為橢圓形的結(jié)論[7-14]。通過眾多學(xué)者的研究，雖然也得出了一些隧道變形相關(guān)的結(jié)論，但是這些變形結(jié)論更多局限在最大位移值或者是隧道橫斷面方向[15-17]，對復(fù)雜的基坑分段開挖時下部盾構(gòu)隧道的縱向變形規(guī)律的研究相對較少，而搞清楚這個問題則顯得尤為重要。

基坑同隧道平面關(guān)系越接近平行，卸載引起的隧道縱向變形范圍越大，越有利于研究隧道的縱向變形規(guī)律。但多數(shù)研究中，基坑和隧道的關(guān)系多為鄰近[18-19]或近似垂直相交[20-21]，小角度長距離斜交的情況較為少見。以徐州市軌道交通1號線杏山子車輛段出入段線基坑小角度斜跨路窩站-杏山子站區(qū)間右線盾構(gòu)隧道為例，通過數(shù)值軟件對分段開挖基坑下盾構(gòu)隧道的縱向變形規(guī)律進行研究。

1 工程概況1.1 項目背景

徐州市軌道交通車輛段出入段線基坑與1號線路窩站-杏山子站區(qū)間右線平面交角約為16°，相交里程K0+737.335。K0+697.000～K0+757.000段為疊交核心區(qū)。核心區(qū)內(nèi)出入段為單洞雙線矩形框架結(jié)構(gòu)，寬10.92～13.07 m，高6.31 m。路杏右線盾構(gòu)隧道外徑為6.2 m，內(nèi)徑為5.5 m，錯縫拼裝結(jié)構(gòu)，基坑開挖前，盾構(gòu)已掘進完畢并即將進入鋪軌階段。核心區(qū)基坑深8.5～9.2 m，坑底與盾構(gòu)隧道豎向凈距約3.0 m。因基坑同隧道小角度斜交，若采用直立開挖，會有較長范圍的圍護樁嵌固過淺，故擬采用放坡法開挖，坡率為1∶2。

1.2 水文地質(zhì)

地層從上至下依次為1-1雜填土、2-5-2粉土、2-2淤泥質(zhì)黏土、2-5-2粉土、2-3-3黏土、2-5-3粉土、2-4-3粉質(zhì)黏土、2-4-4粉質(zhì)黏土、5-3-4黏土層等，坑底主要位于粉土和粉質(zhì)黏土層中，盾構(gòu)隧道主要位于5-3-4黏土層中。地下水類型為孔隙水，位于地面以下0.7～2.7 m。核心區(qū)的平、縱斷面分別見圖1、圖2。

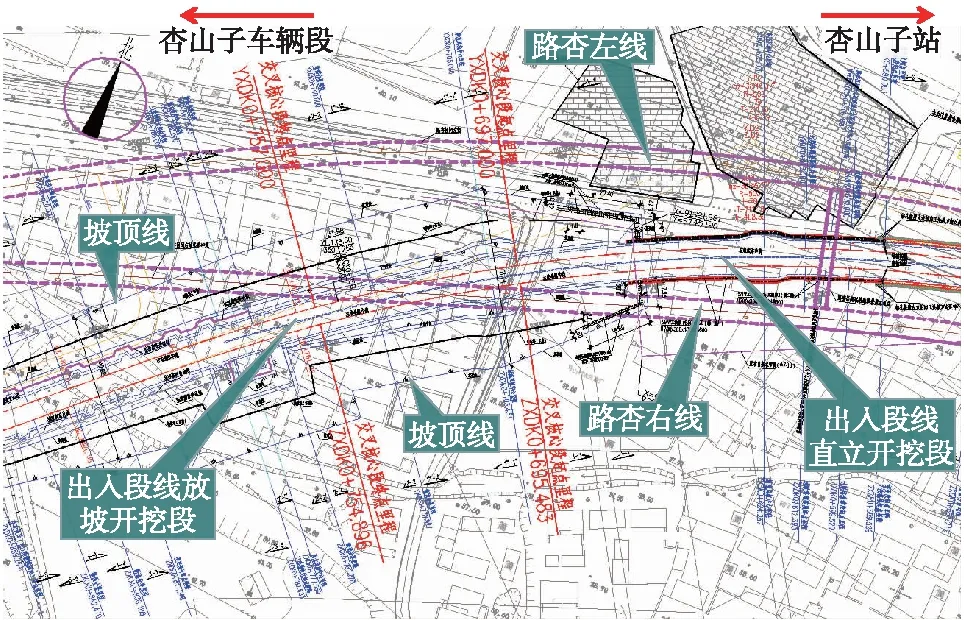
圖1 核心區(qū)平面

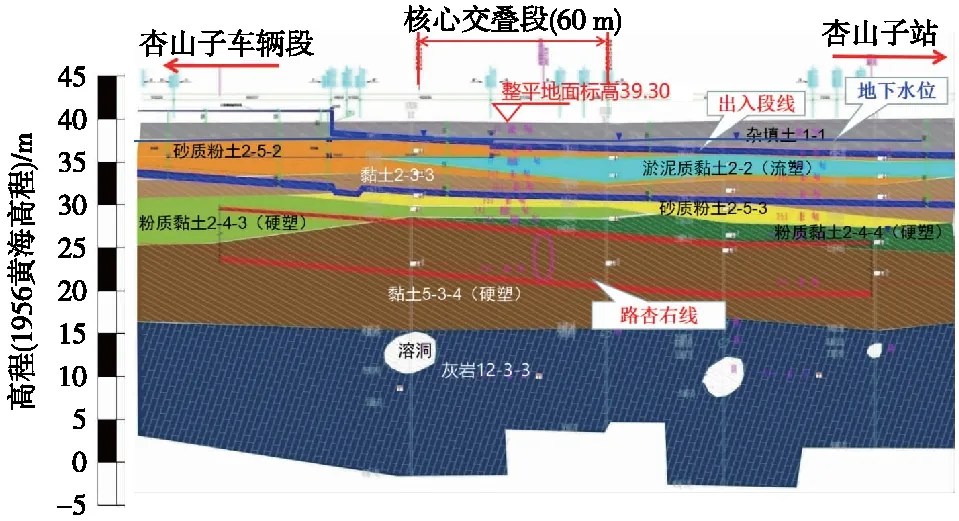
圖2 核心區(qū)地質(zhì)縱斷

2 數(shù)值模擬分析研究

開挖卸載問題是三維問題，具有時間和空間效應(yīng)。數(shù)值模擬則非常適宜處理此類多方案、多工序、多時序的復(fù)雜三維問題。采用Flac3d有限差分軟件進行全過程的三維模擬。

2.1 計算模型

采用Flac3d進行計算。土體、巖體、明挖隧道采用實體單元模擬，土體和巖體為彈塑性、服從摩爾庫倫準(zhǔn)則，明挖隧道為彈性；盾構(gòu)管片采用殼單元進行模擬，取為彈性模型。模型不進行地下水的模擬。模型尺寸為200 m(基坑縱向)×150 m(基坑橫向)×80 m(深)。模型四周施加各向的水平法向約束，模型底部施加豎向法向約束，模型頂面為自由邊界。計算模型見圖3，核心區(qū)60 m基坑與下部隧道的空間關(guān)系見圖4。

圖3 計算模型

圖4 核心區(qū)60 m基坑與下部隧道空間關(guān)系

2.2 模型參數(shù)

根據(jù)勘察報告可得本次數(shù)值模擬的地層和結(jié)構(gòu)參數(shù)，見表1。

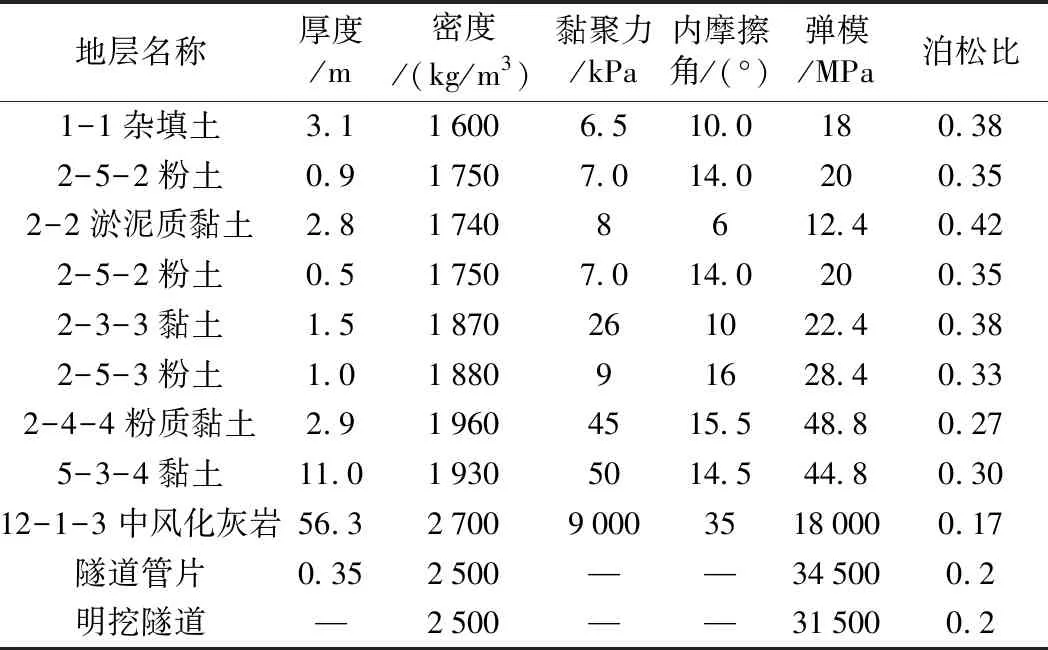
表1 數(shù)值計算模型參數(shù)取值

2.3 數(shù)值計算過程

模型建立后，首先施加重力荷載，形成初始地應(yīng)力；再模擬開挖、施工下部盾構(gòu)隧道，并計算至平衡；對土層、隧道單元位移清零；進行洞內(nèi)預(yù)壓重或基坑開挖工作直至結(jié)束。土體開挖采用Flac3d中的空(Null)模型模擬。

2.4 數(shù)值模擬計算(盾構(gòu)隧道洞內(nèi)無壓重)

分核心區(qū)60 m為3段：大里程20 m(左段、K0+737.000～K0+757.000)、中心里程20 m(中段、K0+717.000～K0+737.000)、小里程20 m(右段、K0+697.000～K0+717.000)。由于疊交段基坑深8.5～9.2 m，故各段基坑均分5層開挖。各段基坑開挖到底后先施工明挖隧道結(jié)構(gòu)，再進行下一分段開挖。具體劃分為7個方案，見表2。

表2 洞內(nèi)無壓重各模擬方案

(1)具體方案介紹

上述7個方案按照各分段不同的開挖順序劃分，可分為4個組合。

①方案一：目的是分析疊交核心區(qū)整體一次性分層開挖時隧道的變形情況，以便與其他方案的計算結(jié)果進行對比。

②方案二和方案三：均為向同一方向的順次開挖，分別為從左向右開挖和從右向左開挖。

③方案四和方案五：均為先開挖兩側(cè)分段后開挖中間分段。

④方案六和方案七：均為先開挖中間分段后開挖兩側(cè)分段。

(2)計算結(jié)果分析

各方案盾構(gòu)隧道出現(xiàn)最大隆起時，豎向位移云圖分別見圖5～圖11；各方案隧道的最大豎向位移值見表3；各方案隧道最大豎向位移值在隧道縱向的出現(xiàn)位置見圖12。

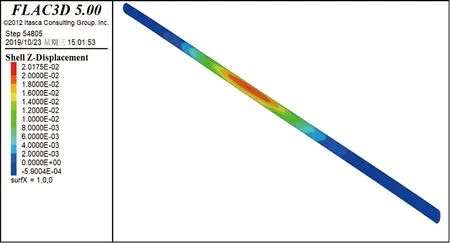
圖5 方案一隧道最大豎向位移云圖

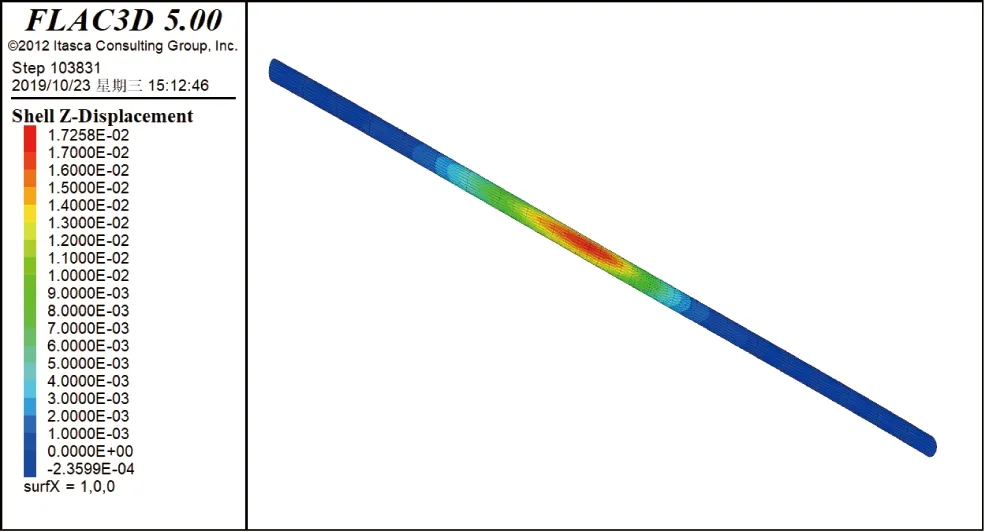
圖6 方案二隧道最大豎向位移云圖

圖7 方案三隧道最大豎向位移云圖

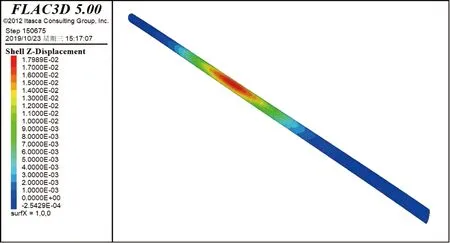
圖8 方案四隧道最大豎向位移云圖

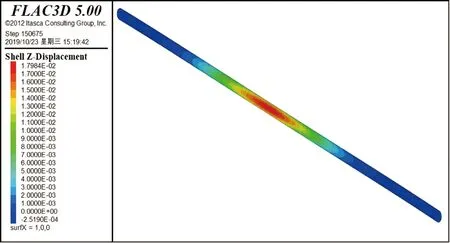
圖9 方案五隧道最大豎向位移云圖

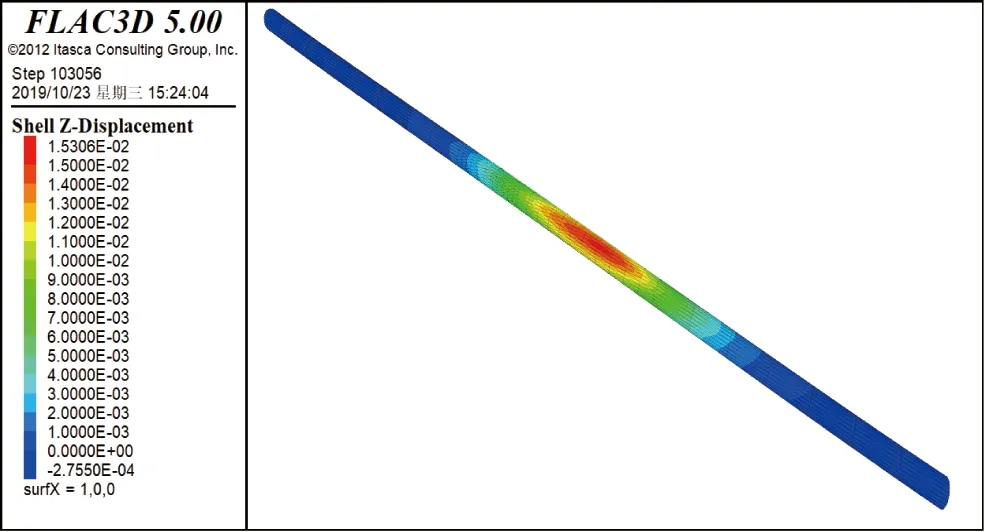
圖10 方案六隧道最大豎向位移云圖

圖11 方案七隧道最大豎向位移云圖

表3 各方案隧道最大豎向位移值對比 mm

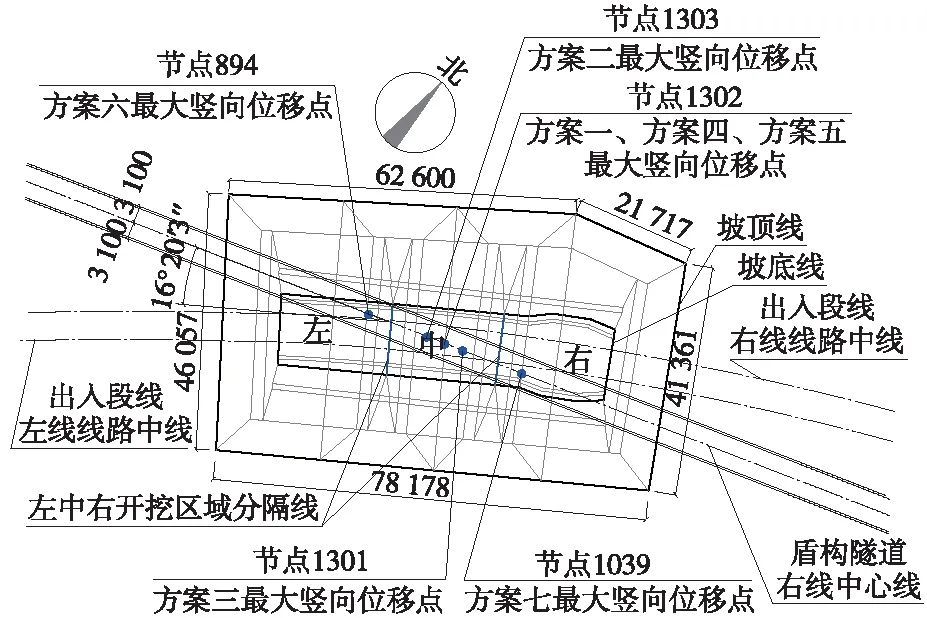
圖12 各方案最大豎向位移點平面位置(單位：mm)

各方案盾構(gòu)隧道最大豎向位移值隧開挖進程的變化趨勢及其相互間的對比關(guān)系見圖13。

注：①開挖a-b,a取值1、2、3，分別代表各方案先開挖段、次開挖段、后開挖段。以方案一舉例，1代表60 m的疊交核心區(qū)；以方案二舉例，1代表左段、2代表中段、3代表右段。②開挖a-b,b取值1、2、3、4、5，分別代表各開挖段從上至下第1、2、3、4、5層土。以方案一舉例，1代表核心區(qū)60 m的第一層土；以方案六為例，1代表各分段的第一層土。③施工主體1、2、3，分別指各方案先開挖段、次開挖段、后開挖段處主體結(jié)構(gòu)。以方案一舉例，1代表核心區(qū)60 m范圍內(nèi)全部主體結(jié)構(gòu)；以方案六為例，1代表中段范圍內(nèi)的主體結(jié)構(gòu)。④水平軸不是單純的豎向深度或縱向長度，同時有土層豎向深度和各分段先后疊加的含義，重在展示整個開挖過程的時空趨勢。圖13 各方案隧道最大豎向位移變化趨勢對比

從圖5～圖11、表3中可以得出如下結(jié)論。

①整體開挖時盾構(gòu)隧道最大隆起位移值和隧道隆起范圍均明顯大于分段開挖時。開挖分段越多越短，盾構(gòu)隧道的最大隆起位移值越小，隧道隆起范圍越小。

②最大豎向隆起位移均出現(xiàn)在隧道拱頂。

③先開挖核心區(qū)中段基坑時，開挖對隧道隆起的影響范圍最小。

④以最大隆起位移作為主要標(biāo)準(zhǔn)，方案六最優(yōu)，即最優(yōu)開挖順序為中段、左段、右段。

從圖12中可以得出如下結(jié)論。

①最大隆起位移在盾構(gòu)隧道縱向出現(xiàn)的位置與開挖順序呈現(xiàn)比較明顯的相關(guān)性。方案一、方案四、方案五最大豎向位移點出現(xiàn)位置相同，其位置基本對應(yīng)基坑中心；方案二和方案三最大豎向位移點出現(xiàn)位置，相對靠近基坑中心并呈左右對稱關(guān)系；方案六和方案七最大豎向位移點出現(xiàn)位置相對遠(yuǎn)離基坑中心，并呈左右對稱關(guān)系。

從圖13中可以得出如下結(jié)論。

①開挖分段個數(shù)與趨勢圖中位移峰值個數(shù)相同。

②首段開挖時，各方案隧道最大隆起位移隨開挖深度線性增加，整體一次性開挖時斜率明顯大于分段時。次段和后段開挖時，隧道最大隆起位移隨開挖深度近似線性增加，斜率明顯小于首段開挖時。

③施工出入段線主體后，隧道隆起位移均有比較明顯的回落，回落數(shù)值與主體質(zhì)量、回填土質(zhì)量呈正相關(guān)。

④施工各主體后的第一次開挖，隧道隆起位移均出現(xiàn)未升反降的特點。說明后次開挖對前次開挖段下部隧道的隆起變形進行適當(dāng)平衡，是隧道整體性的體現(xiàn)，但是調(diào)整幅度有限。后次開挖段的變形速率明顯小于前次開挖段，也證明隧道整體性對最大隆起位移的舒緩作用。根據(jù)計算結(jié)果進行統(tǒng)計，此作用對位移的單向調(diào)整比率約為5.71%。

2.5 數(shù)值模擬計算(盾構(gòu)隧道洞內(nèi)預(yù)壓重)

以方案六為基礎(chǔ)，研究洞內(nèi)壓重激勵對基坑分段開挖卸載時下部盾構(gòu)隧道變形規(guī)律的影響。

(1)洞內(nèi)預(yù)壓重方案介紹

盾構(gòu)隧道洞內(nèi)壓重范圍為路杏區(qū)間右線右DK2+365.000～右DK2+455.000，共90 m，范圍為根據(jù)盾構(gòu)隧道和出入段線放坡基坑的平面位置關(guān)系綜合確定。每延米洞內(nèi)壓重分別取0，50，100，150，200，250，300，350，400 kN(共9種)。洞內(nèi)預(yù)壓重且計算至平衡后，方可按照方案六進行開挖施工。

(2)計算結(jié)果分析

①不同壓重級別下隧道沉降情況

預(yù)壓重工況時，不同壓重級別下隧道最大沉降值和隧道最大沉降值隨壓重量的變化曲線分別見表4和圖14。

表4 各壓重級別時盾構(gòu)隧道最大沉降值對比

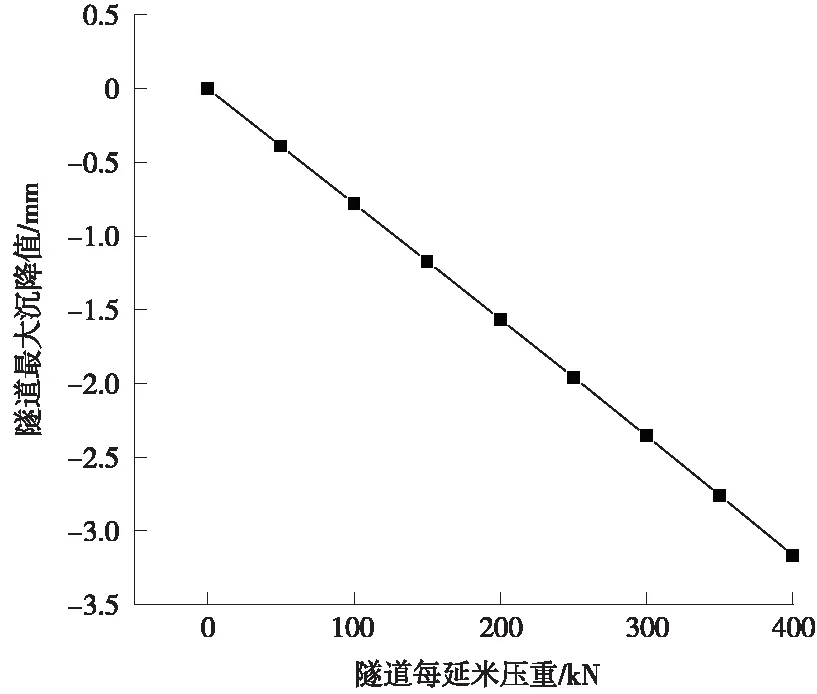
圖14 預(yù)壓時隧道最大沉降值隨壓重變化趨勢

②盾構(gòu)隧道最大隆起位移變化趨勢

不同壓重下，隧道最大豎向位移隨開挖進程的變化趨勢見圖15；壓重狀態(tài)與無壓重狀態(tài)下隧道最大豎向位移值差值隨開挖進程的變化趨勢見圖16。

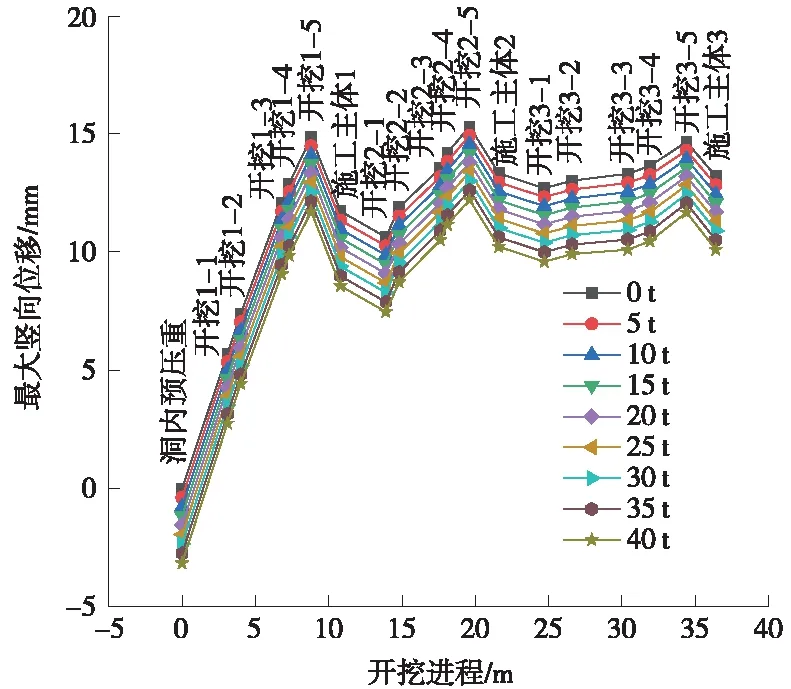
圖15 各壓重級別時隧道最大豎向位移變化趨勢

圖16 隧道最大豎向位移差值變化趨勢

從圖14和表4中可以得出如下結(jié)論。

①隧道沉降值隨預(yù)壓質(zhì)量增加而線性增大。

②就本工程而言，使盾構(gòu)隧道隆起減小1 mm，需要壓重約126.4 kN。由于耗費相對較大，綜合考慮造價、對全線工期影響、便宜性等因素后，選擇50 kN作為本工程的洞內(nèi)壓重。

從圖15可以得出如下結(jié)論。

洞內(nèi)預(yù)壓并未改變隧道隆起的變形趨勢；不同壓重級別時隧道的變形曲線呈近似平行關(guān)系。

從圖16可以得出如下結(jié)論。

隨著開挖的進行，洞內(nèi)壓重對隧道最大豎向位移的影響呈波浪形，壓重越大波浪形特征越明顯。這種特性屬于壓重激勵時，隧道的整體性對各相鄰部分結(jié)構(gòu)彼此變形的調(diào)整，根據(jù)計算結(jié)果進行統(tǒng)計，調(diào)整比率約在5.71%。此數(shù)值與卸載方案時得出的結(jié)論高度對應(yīng)。

3 結(jié)論

(1)基坑分段越短，下部盾構(gòu)隧道的最大隆起位移值越小，同時隧道隆起范圍越小。開挖分段個數(shù)與隧道隆起位移峰值的個數(shù)相同，其分段越均勻，峰值大小越接近。

(2)應(yīng)優(yōu)先開挖疊交核心區(qū)中段基坑，而非兩側(cè)基坑。

(3)隧道縱向各相鄰部位對彼此變形的單向調(diào)整比率約為5.71%。

(4)分段開挖時，盾構(gòu)隧道最大隆起點出現(xiàn)位置呈現(xiàn)規(guī)律性：中段先開挖時，最大隆起點位置位于次開挖段；中段次開挖時，最大隆起點位置位于中段靠近先開挖段部分；中段后開挖或整體一次性開挖時，最大隆起點位置均位于中段基坑中部。可在一定范圍內(nèi)，利用上述規(guī)律，通過調(diào)整開挖順序，可選擇讓最大豎向隆起位移出現(xiàn)在隧道相對健康的位置，或環(huán)境和自身風(fēng)險相對較低的位置。