電遷移誘發夾雜形貌演化的相場模擬
張嘉明,黃佩珍
(南京航空航天大學機械結構力學及控制國家重點實驗室,江蘇南京 210016)
在生產、服役過程中,內連導線承受著高電流密度,其中大量的電子流做定向運動,形成逆電場方向的“電子風”,與金屬粒子碰撞發生動量傳遞,導致金屬粒子朝著逆電場方向運動。這種現象被稱之為電遷移,對內連導線的可靠性有顯著影響[1]。在電遷移作用下,內連導線中諸如孔洞、夾雜等微缺陷會發生漂移以及形變,其形貌可能會失穩、分裂或聚合[2]。因此,研究電遷移誘發界面擴散下夾雜的形貌演化機理,對于了解金屬內連導線的微觀特性,改善微電子器件的可靠性具有重要意義。
近年來,迅速發展的相場法為研究微結構演化提供了強有力的工具[3]。結合動力學和熱力學定律,相場理論中有兩類常見的方程,分別為Cahn-Hilliard方程[4]和Allen-Cahn方程[5]。其中,Cahn-Hilliard方程描述了滿足質量守恒定律的原子擴散過程,用于研究Spinodal分解、表面擴散[6-10]等問題。
Mahadevan等[6]最早建立了電遷移的相場模型并進行了漸進分析。Bhate等[7]采用非光滑雙阱勢構造了相場模型,用于研究電遷移和應力誘發表面擴散、體擴散下孔洞的演化。Barrett等[8]基于退化型遷移率模擬了孔洞的電遷移行為。Li等[9]研究了電導率和各向異性表面能對電場作用下夾雜遷移和演化的影響。Santoki等[10]研究了各向異性表面能作用下圓形夾雜的演化。
在上述相場研究工作中,未見文獻報道體自由能密度和退化型遷移率均采取四次雙阱勢函數的相場模型。本文應用開源框架MOOSE[11]編制有限元程序,分析了橢圓夾雜在電遷移作用下的基本演化規律,以及電場強度和初始形態比對不同電導率的夾雜演化規律的影響。
1 基本理論
如圖1所示,考慮基于平面應變問題的二維內連導線單晶模型,初始夾雜存在于有限大的金屬基體中,內連導線兩端施加大小為φ∞的電勢差。l、h分別為導線的線長與線寬,a、b分別為x、y軸上微缺陷的半軸長,β=a b,為形態比。序參數φ用于區分基體和夾雜的不同相,將模型分為三個區域:基體區域R+中φ=+1,夾雜區域R-中φ=-1,界面層RI內φ由-1到+1連續變化。
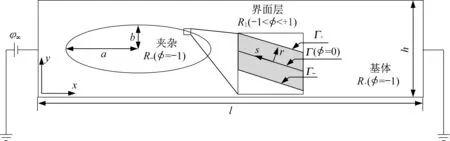
圖1 內連導線中夾雜的相場模型Fig.1 Phase field model of an inclusion in the interconnect line
在外電場作用下,系統的總自由能泛函F構造形式為
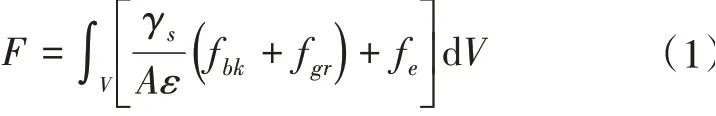
式(1)中,γs為界面張力,ε為與界面層厚度相關的梯度能量系數,A=4 2W3為無量綱參數,其中W表示兩個平衡相之間的勢壘高度。系統的總自由能密度F由體自由能密度fbk、梯度自由能密度fgr和電勢能密度fe組成,分別為
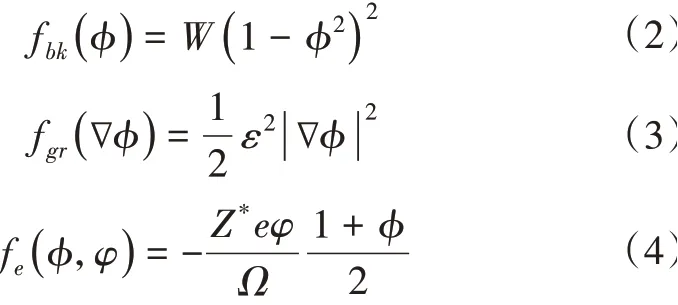
式(2)中的fbk采用四次雙阱勢函數。式(4)中,φ為電勢,Ω為遷移原子體積,Z*為原子的有效化合鍵,e為元電荷。化學勢μ由F對φ的變分導數定義,即
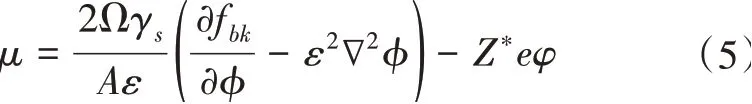
式(5)中,因子2是由于從R-到R+中φ由-1過渡為+1所致。界面原子的質流通量J與?μ(驅動力)呈線性關系,即
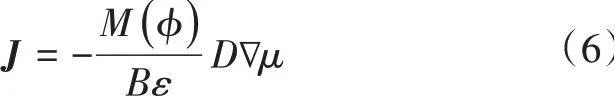
式(6)中,B=2 3 2W為無量綱參數,D為界面擴散的原子遷移率。M(φ)表示與φ相關的退化型遷移系數,即
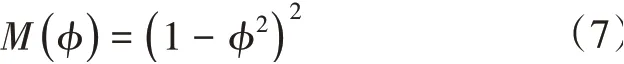
式(7)確保了原子的界面擴散只發生在RI內。根據質量守恒定律,φ對時間t的變化率與J的散度有關,即

式(8)即為四階修正的Cahn-Hilliard方程,即
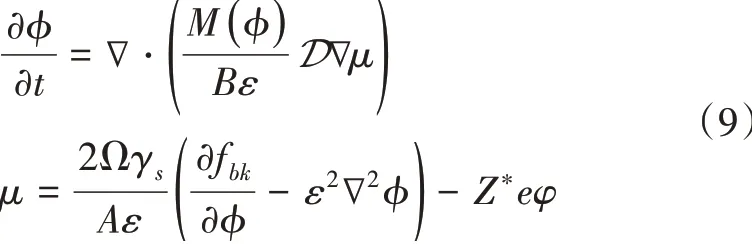
求解式(9)需要聯立φ的拉普拉斯方程,即
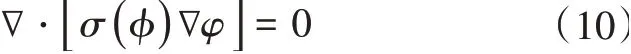
式(10)中,σ=σ(φ)表示與φ相關的電導率。
2 可靠性驗證
基于所推導的相場控制方程,應用MOOSE編制有限元程序。為了驗證程序可靠性,考慮無限大且各向同性金屬材料中半徑為R的圓形夾雜,在小電場下保持圓形并沿電場方向穩定漂移的理論解[12],即
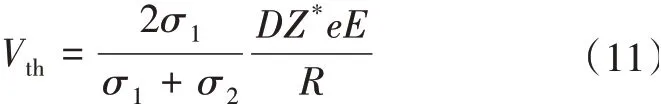
式(11)中,E=φ∞l表示遠端電場強度。
定義特征速度Vf=DΩγs af3,相對電場強度χ=,采用無量綱時間t~=tDΩγs af4。將夾雜漂移速度的理論解和數值解分別無量綱化,即

下標th和num分別表示理論解和數值解。由圖2可見,數值解V~num與理論解V~th吻合良好,故本文的有限元算法是可靠的。
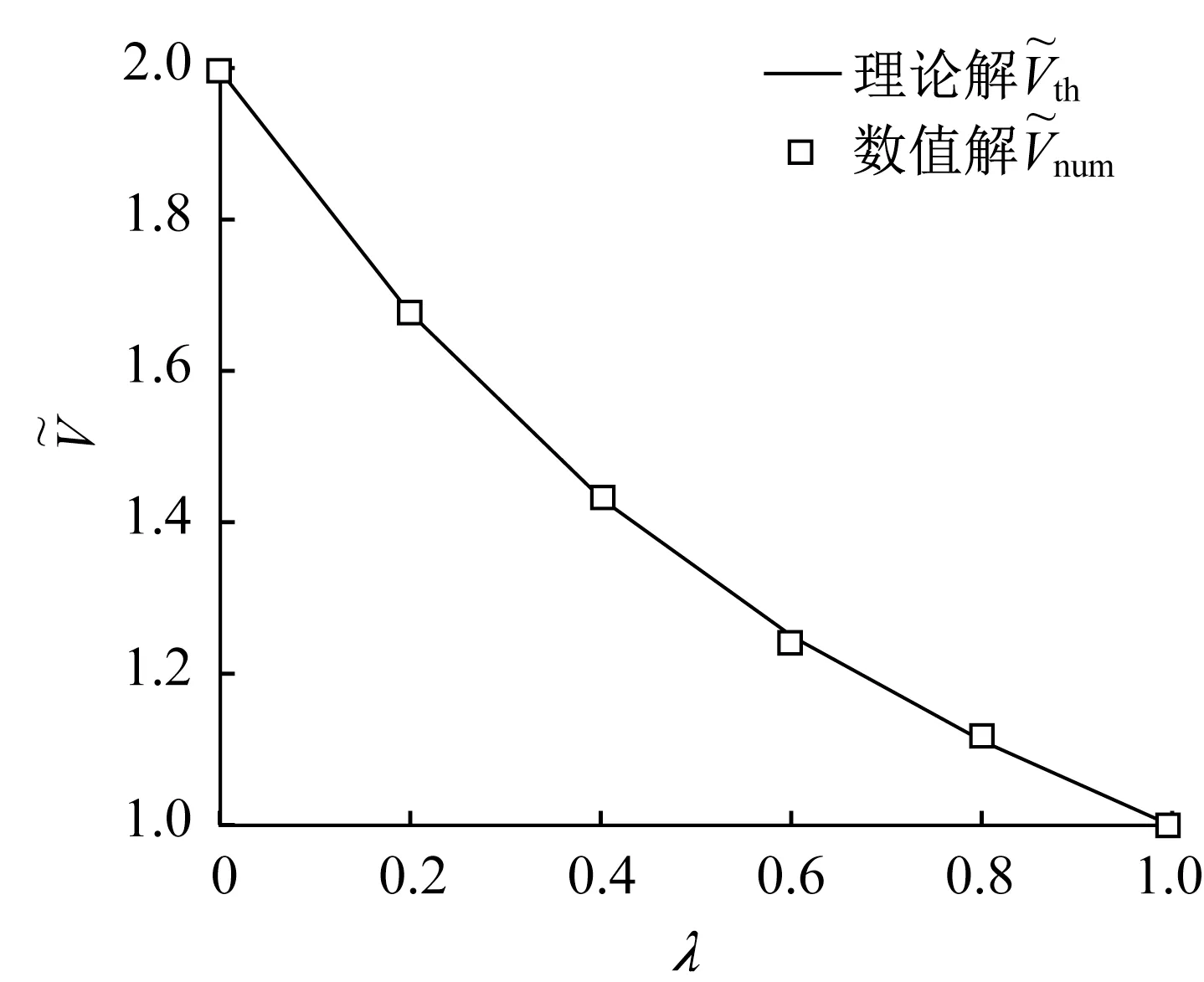
圖2 夾雜的漂移速度V~隨著λ的變化曲線Fig.2 The variation curve of drift velocity V~of inclusion withλ
3 數值模擬與討論
下面將分析電遷移誘發界面擴散下夾雜的形貌演化規律,討論χ和β對不同λ的夾雜形貌演化的影響,其中外電場的方向均為從左向右。
3.1 相對電場強度χ的影響
圖3-4為χ=4,12且β=3時,不同λ下夾雜的形貌演化圖。由圖3可見,夾雜均沿電場方向穩定漂移,λ=0的夾雜前方形成刻面,而λ=0.5的夾雜僅后方完成圓柱化。由圖4可見,λ=0的夾雜沿x軸方向發生分裂,而λ=0.5的夾雜前方形成逐漸拉長的指狀延伸。
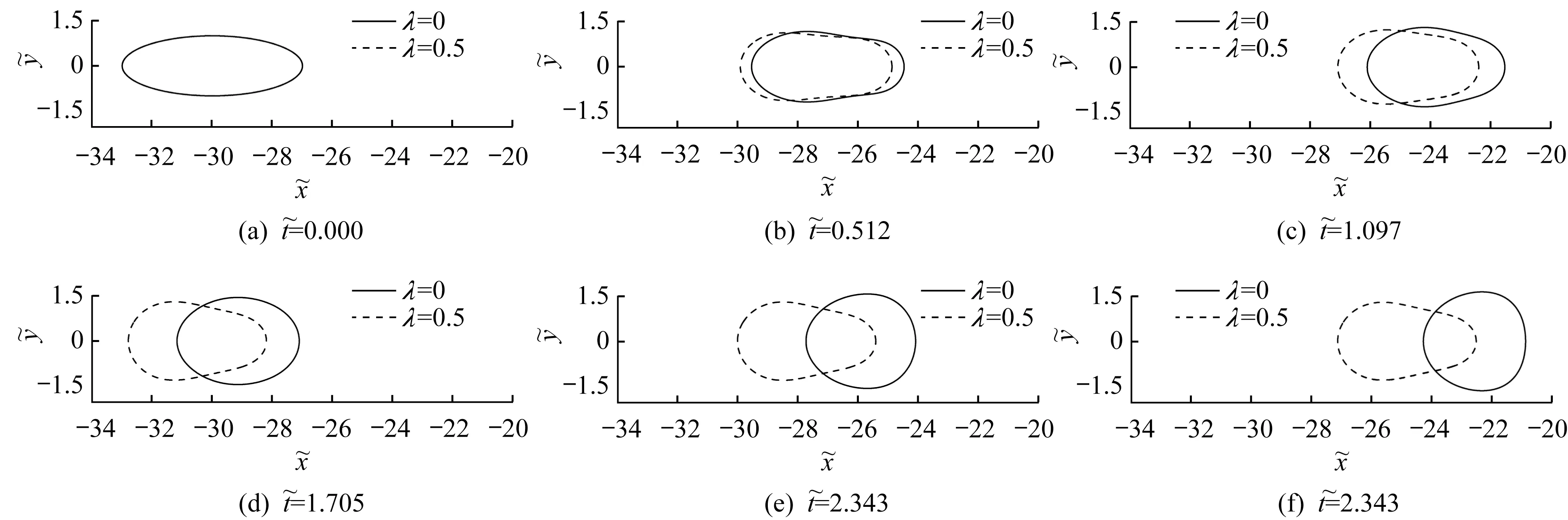
圖3 χ=4,β=3時,不同λ下夾雜的形貌演化圖Fig.3 Morphological evolution of the inclusions under differentλforχ=4,β=3
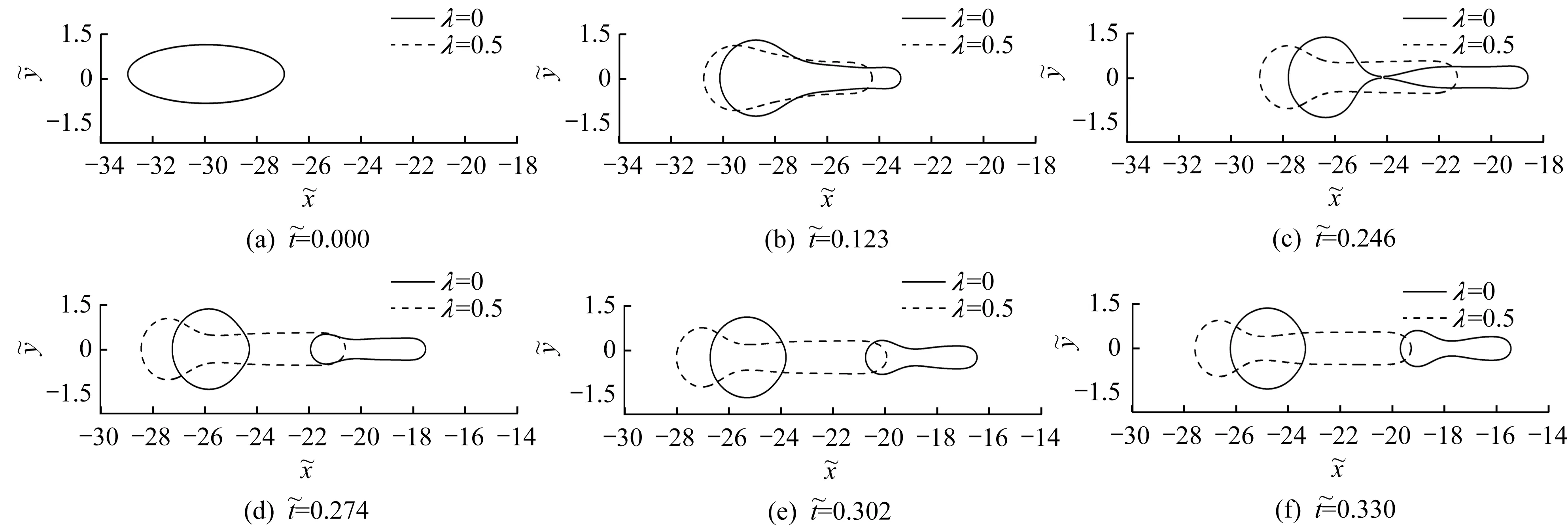
圖4 χ=12,β=3時,不同λ下夾雜的形貌演化圖Fig.4 Morphological evolution of the inclusions under differentλforχ=12,β=3
3.2 初始形態比β的影響
圖5-6所示為β=3,5且χ=20時,不同λ下夾雜的形貌演化圖。由圖5可見,λ=0的夾雜沿x軸方向發生分裂,而λ=0.5的夾雜先后沿x軸方向和y軸方向發生分裂。由圖6可見,λ=0的夾雜分裂時間相比圖5更長,且發生了多次分裂,而λ=0.5的夾雜形成了狹長指狀延伸。

圖5 β=3,χ=20時,不同λ下夾雜的形貌演化圖Fig.5 Morphological evolution of the inclusions under differentλforβ=3,χ=20

圖6 β=5,χ=20時,不同λ下夾雜的形貌演化圖Fig.6 Morphological evolution of the inclusions under differentλforβ=5,χ=20
4 結 論
本文相場模擬了相對電場強度χ和初始形態比β對不同電導率λ的夾雜形貌演化的影響,得到主要結論如下:
(1)在電遷移作用下,夾雜沿電場方向發生漂移,且λ越大,夾雜的漂移速度越慢。
(2)對于一定β的夾雜,λ越大,夾雜分裂時所需的χ越大。
(3)當χ較大、β較大時,λ小的夾雜容易分裂;β較小時,λ大的夾雜容易分裂。

