數學抽象概括能力的培養之模式化教學方式
羅容清

摘 要:國際象棋大師除了習得了50000種不同的國際象棋模式,還學會了怎樣應對這些模式。我們教學生數學,也采用模式化的教學方式,除了可以提高學生的應試能力和數學抽象概括能力。抽象概括主要包括兩個方面。第一,對知識的概括;第二,對方法的概括。
關鍵字:模式;抽象概括能力;定理和概念教學程序化;解題模式化
專家們試圖找出國際象棋大師和較弱的棋手之間的主要區別,在德格魯特(De groot,1956,1966)的研究中發現,國際象棋大師估計習得了50000種不同的國際象棋模式,并且他們能夠很快的在棋局中識別這些模式。記憶這么多的模式和在國際象棋比賽中的優異表現之間有什么聯系?紐厄爾和西蒙(Newell&Simon,1972)推測,除了學習了許多模式以外,大師們還學會了怎樣應對這些模式。大師能夠有效地“看到”可能的著法,而不需要思考它們。這就說明了為什么國際象棋大師擅長于幾秒鐘一步的快棋賽。了解了這個例子,我陷入了沉思:這給我們的數學教學以什么啟示?如果我們教學生數學,也采用模式化的教學方式,除了可以提高學生的應試能力——就像國際象棋大師一樣,同時他們的數學抽象概括能力應該也是可以獲得提高。
我國著名數學教育家,數學教育心理學研究的開創者和奠基人曹才翰指出了數學概括的兩層含義:其一,指在思想上把具有相同本質特性的事物聯系起來;其二,是把被研究對象的本質特性推廣位范圍更廣的包含這個對象的同類事物的本質特性。
數學抽象概括能力一般表現在以下幾個方面:(1)數學語言意義的概括能力;(2)數學概念的概括能力;(3)對數學知識結構的概括能力;(4)數學思想方法的概括。
數學學習必須通過解決問題去理解和鞏固知識,而解決問題是訓練學生抽象概括能力的一種有效途徑。在解決問題中,抽象概括主要包括兩個方面。第一,對知識的概括,也即是對數學語言意義和數學概念的概括。第二,對方法的概括。也即是對數學知識結構和數學思想方法的概括。解決問題除了要用到某些知識外,必然要用到某些某些方法,一種方法往往可能具有一般性,它不僅可以用來解決一個問題,還有可能用來解決一類問題,對解決當前問題要對這個問題進行歸類,把這個問題置于某種數學方法的統領之下,形成一種以方法統攝知識的體系。
在解題教學中,教師要訓練學生在知識和方法兩個方面的概括意識和概括能力。具體的做法可以參考如下幾點:
一:定理和概念教學程序化,促進學生對陳述性的知識和精深加工,最終形成應用模式
數學程序性知識是由陳述性知識轉化而來的,是陳述性知識的動態成分。它是以“產生式”這種動態形式來表征,一個產生式總是對某一或某些特定的條件滿足時才發生的某種行為的一種程序。當一個產生式的行動成為另一個產生式的條件時,這兩個產生式便建立了相互的聯系。它同時還是一種雙向產生式。“雙向產生式”是指一種具有雙重功能的指令,它既能指令在具備什么樣的條件下會有什么動作,又能指令在不同的情形中選用不同的產生式。換言之,學習者不僅知道一條“如果......那么……”規則,而且還應該知道在什么條件下使用這條規則。
由此學生不再依賴于逐字的回憶定理內容,而是把定理的應用抽象概括成了一個模式。模式識別是技能程序化的一個重要部分。我們不必再思考下一步做什么,我們只要識別什么事適合于當前情境的做法。
二:解題模式化
解決問題重在對問題的表征,深入理解題意,尋找解決當前問題的遷移源,而不是盲目地“試誤”;重在對問題解決后的反思,重在培養學生對模式和方法的概括能力,從現實問題中概括出具體的數學題型的模型。
所以,樣例的教學中,為了讓學生能夠模仿樣例進而超越樣例去解決問題,老師可以引導學生抽象概括出解這一類型題的解題模式。也就是把一些相同相似的同類的題例放在一起,找出規律,尋找相同點和不同點,概括總結出共性,進而撒下探究的“種子”。讓 同學們總結歸納同類型題的解決方法,并注意探究和發掘變化的事物中蘊含的一般規律。主動嘗試變化的過程,探求其中的奧妙,最終抽象概括出解題模式。
例如,對于任意實數x,y,總有,若令,則x=a+b,y=a-b。這個二元代換可以用于解決一類問題。
例 實數x,y滿足4x2-5xy+4y2=5,設S=x2+y2,
分析? 令x=a+b,y=a-b,代入已知等式化簡,得
。
由于,得從而
由此,容易求得Smax和Smin值.
又如七年級學了平行線的性質后,有如下類似的題:
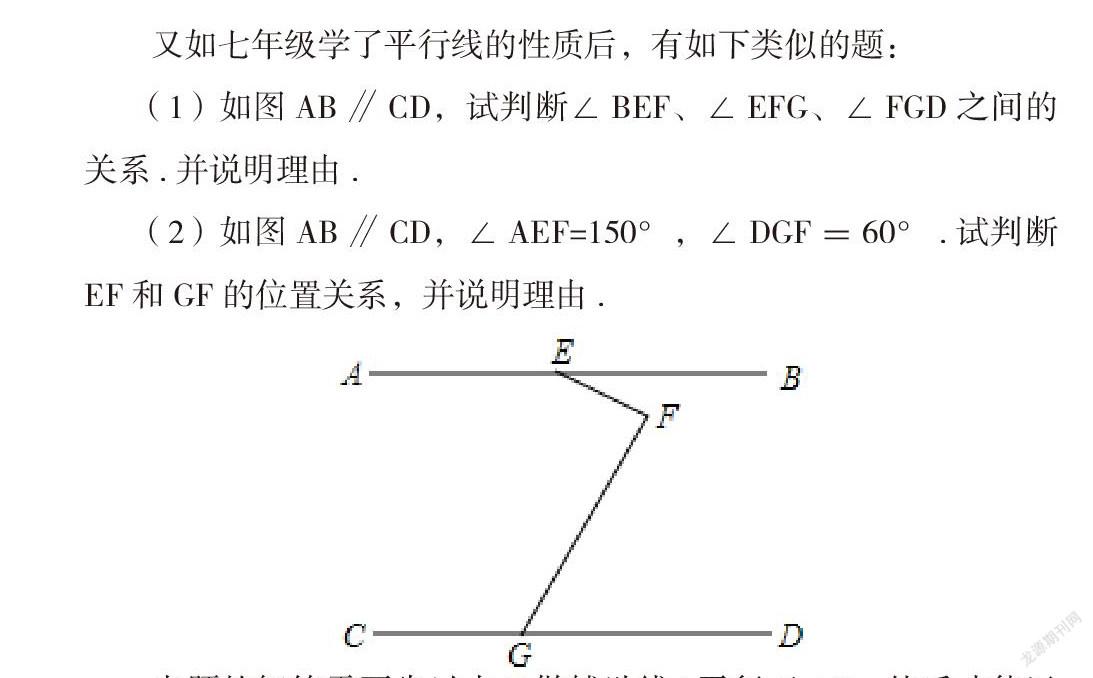
(1)如圖AB∥CD,試判斷∠BEF、∠EFG、∠FGD之間的關系.并說明理由.
(2)如圖AB∥CD,∠AEF=150°,∠DGF=60°.試判斷EF和GF的位置關系,并說明理由.
本題的解答需要先過點F做輔助線l平行于AB,然后才能運用平行線的性質來求解。這對于七年級的大多數學生來說,他們的數學抽象概括能力,主要還停留在小學的水平,對于添加輔助線還沒有任何的概念,所以這就需要老師利用多個類似的樣題和練習,引導學生抽象概括出這種題型作輔助線的條件,從而總結出解題模式。
三:課后反思歸納分類總結題型的解題模式
除了樣例的教學中,老師要有意識的引導學生抽象概括出解這一類型題的解題模式。平時的作業,或階段復習時也可以布置學生去收集同類型題,然后逐步讓學生半獨立,獨立地概括總結出其解題模式,老師進行評價和總結。經過訓練,學生就能夠識別在很多問題中重復出現的各種要素及其模式,當這些模式出現時,不假思索就知道該怎么做。通過一個個解題模式,掌握問題解決規則和適當的問題解決組織方式,讓學生學會舉一反三,觸類旁通,以不變應萬變。使學生在變化的多個習題中,發現不變的規律,從而提高解決問題的能力,抽象概括能力也隨之獲得提高。
參考文獻:
[1]張英伯,曹一鳴《數學教學心理學》,北京師范大學出版社
[2]約翰.安德森《認知心理學及其啟示》第七版,人民郵電出版社
1547500783364

