基于等效電導率的壓接型IGBT器件溫度場仿真

何智鵬，李巖，侯婷，姬煜軻

(直流輸電技術國家重點實驗室(南方電網科學研究院)，廣州510663)

0 引言

壓接型絕緣柵雙極型晶體管(insulated gate bipolar transistor，IGBT)器件具有無焊接點，無引線，低熱阻的特點，因此其流通能力相較于傳統的焊接式IGBT器件由較大提高，因此常被應用在高壓大功率場合[1]。隨著近年來大容量柔性直流輸電工程的大規模建設，對于壓接型IGBT器件的使用將越來越多，大有取代傳統焊接式IGBT器件成為市場應用主流的趨勢[2]。因此，對于運行狀態下壓接型IGBT器件可靠性研究以及壽命預測有十分重要的意義[3 - 4]。

由于沒有焊層和鍵合引線，壓接型IGBT器件的失效模式與傳統焊接式IGBT器件存在差異，主要存在微動磨損，彈簧失效，芯片斷裂等幾種失效模式[5 - 6]。究其原因，都是由于在器件工作時，芯片產生周期性的溫度波動，由于多層結構不同材料之間熱膨脹系數(coefficient of thermal expansion, CTE)存在差異，使得接觸面上產生熱應力，導致材料出現老化，進而導致器件失效[7]。因此，得到運行狀態下壓接型IGBT器件內部溫度分布，對于器件可靠性評估以及壽命預測存在重要意義[8]。

有限元分析(finite element analysis, FEA)是壓接型IGBT器件溫度分布計算的常用工具，而有限元模型的準確性極大地影響仿真計算結果[9]。對于壓接型IGBT器件溫度場仿真，設置基于工況的芯片載荷對于模擬實際工況下該器件內部溫度分布十分重要，然而現有研究對該問題涉及不多。文獻[10]通過對整體器件的導通損耗以及開關損耗的計算得到器件內部總的發熱功率，再對每個芯片取平均值作為單個芯片的發熱功率。這一方法沒有考慮由于幾何不對稱性以及溫度不均勻造成的器件內部芯片之間發熱功率的差異。文獻[11]考慮了器件內芯片發熱功率接觸電阻接觸熱阻以及溫度分布影響呈現的差異性，但未控制器件集電極電流為定值，因而會導致單個芯片發熱功率總和超過器件整體發熱功率問題。文獻[12]建立了單芯片有限元模型，控制母線電流為50 A恒定，然而文獻中簡化模型與實際壓接型IGBT器件還存在一定差異。本文提出了基于工況的壓接型IGBT器件內部溫度分布預測仿真辦法，通過提出芯片等效電導率概念，以反應芯片損耗隨芯片結溫變化的特性，以及由于幾何不對稱和溫度分布不均勻造成的芯片間損耗差異的特性，該仿真辦法能夠更加準確地反映系統運行時，壓接型IGBT器件內部溫度的分布情況。另外，本文還應用該仿真方法，對三相MMC系統進行仿真分析。

1 壓接型IGBT結構

圖1為某型號壓接型IGBT器件3D模型。

圖1 某型號壓接型IGBT器件結構示意圖Fig.1 Sketch diagram of the structure of a press-pack IGBT module

圖中自下而上依次為集電極凸臺、集電極鉬片、芯片、發射極鉬片和發射極凸臺。整個器件包含21塊芯片，此外，門極彈簧、印刷電路板(printed circuit board, PCB)等結構在建模中忽略。整個結構由外部裝配力緊密壓接，底部放置碟簧以平衡熱應力帶來的形變。

2 基于等效電導率的壓接型IGBT器件仿真模型

有限元仿真是得到壓接型IGBT器件內部溫度分布的重要方法，而芯片發熱功率的設置對于仿真結果的準確性有很大影響[13]。本文提出了基于等效電導率的思想進行仿真載荷設置。

當電流流過器件時，由于幾何的不對稱性，器件內部各芯片上流過電流不相等，電流的不均衡導致發熱功率差異，進一步引起結溫分布不均勻，而結溫又對芯片發熱功率產生影響[14]。因此，本文引入了芯片等效電導率，即設置芯片材料電導率與溫度相關以反映芯片發熱功率隨溫度變化的特性，使得當額定電流流過功率器件時，芯片總產熱量與器件產熱量相等。這時，芯片上發熱功率分布就是壓接型IGBT器件運行工況下的分布情況。

具體的原理為，假設IGBT器件運行時，內部損耗過程為歐姆損耗，即：

p=f(Tj)=Ic2R(T)

(1)

式中：Tj為芯片結溫；IC為器件集電極平均電流；R(T)為由溫度決定的芯片等效電阻。而芯片材料的電導率，可以通過電阻公式推導如式(2)所示。

(2)

式中：L為芯片厚度；S為器件內部所有芯片總面積。綜合以上兩式，可以得到一個和溫度直接相關的芯片電導率的計算公式如式(3)所示。

(3)

式中P(T)為隨溫度變化的芯片發熱功率。

因此，P(T)是計算芯片等效電導率的關鍵，該發熱功率由器件熱特性以及運行工況共同決定。隨后，以MMC工況為例，進行基于該仿真模型的壓接型IGBT器件溫度場仿真。

3 MMC結構及工作原理

3.1 子器件工作原理

子器件拓撲結構如圖2所示，T1和T2為IGBT，D1和D2為反并聯二極管；C0為子器件直流側電容；uC為電容電壓；usm為子器件兩端電壓也是子器件的輸出電壓；ism為流入子器件的電流。

子器件上下IGBT T1、T2開關狀態以及電流方向ism的不同，會出現子器件“投入”以及“旁路”兩種狀態，分別對應子器件輸出電壓為電容電壓uC和0 V[15]。

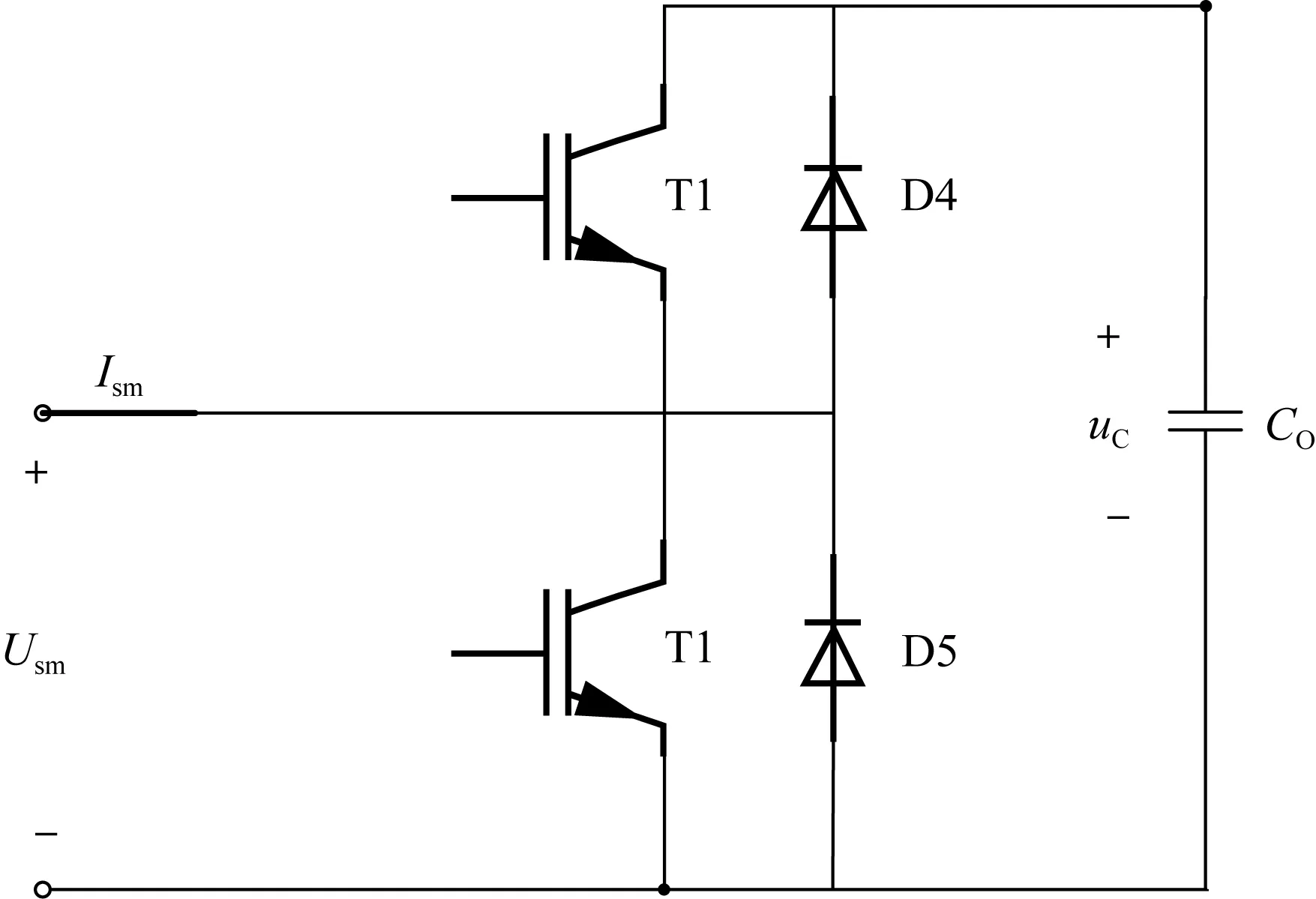
圖2 MMC子器件結構示意圖Fig.2 Sketch diagram of the structure of MMC sub-module

3.2 三相MMC系統工作原理

三相MMC系統結構示意圖如圖3所示，每相單元由10個子器件構成，上下橋臂分別有5個子器件。

圖3 三相MMC系統結構示意圖Fig.3 Sketch diagram for the structure of three-phase MMC system

MMC系統運行滿足2個條件：

1)維持直流側電壓恒定。根據圖3可知，在假設每個子器件電容電壓不變的前提下，就要保證3個相單元中處于投入狀態的子器件數目不變且相等。即：

upa+una=Udc

(4)

式中：upa為a相上橋臂投入子器件的總電壓；una為a相下橋臂投入子器件的總電壓；Udc為系統直流側電壓。

2)在交流側輸出三相交流電壓。通過對3個相單元上下橋臂中投入的子器件數進行調節，從而實現三相交流電壓的輸出，即通過改變每一時刻上下橋臂投入的子器件個數，使得交流側電壓形成正弦波。

4 器件損耗計算

4.1 三相MMC系統電流計算

在MMC工況下，子器件中壓接型IGBT器件損耗由運行過程中子器件平均電流和平均電壓決定。考慮簡化三相MMC系統模型如圖3所示，每相上下橋臂各包含5個子器件，其中直流側電壓Udc為±2 250 V，調制比m為0.9，設置單子器件額定電容電壓值為900 V。三相負載為阻感負載，電感值L為0.005 H，電阻值R為2 Ω。a相相電壓Ua、三相上下橋臂電抗L、a相相電流ia和直流側電流Idc分別由式(5)—(8)得到。

(5)

(6)

(7)

(8)

橋臂電流iau可由式(9)得到。

(9)

而流經子器件的電流為橋臂電流有效值[16]。

4.2 MMC工況下壓接型IGBT器件損耗計算

IGBT器件功率損耗模型中主要包含3個部分的損耗：1)靜態損耗，包含通態損耗PTcon和截止損耗；2)開關損耗PTsw，包含開通損耗和關斷損耗；3)驅動損耗。其中，IGBT器件的驅動損耗和截止損耗在整體損耗中占很少比重的部分，在本文的計算的精度范圍之內可以忽略[17]。

則IGBT總功率損耗PTtot可以表示為：

PTtot=PTcon+PTsw

(10)

式中PTcon和PTsw分別為器件通態損耗和開關損耗。

IGBT通態損耗的計算可以通過擬合集射極電壓Vce和電流IC的關系得到，如式(11)所示。

VCE(Tj)=RT(Tj)·IC+VCEO

(11)

式中：Vce為器件導通壓降；RT為器件等效通態電阻VCE0為擎柱電壓。RT和VCE0都是結溫Tj的函數。該函數關系可由器件的數據手冊得到。則器件通態損耗PTcon可表示為：

PTcon=VCEIC=(RTIC+VCEO)·IC=f(IC,Tj)

(12)

器件的開關損耗主要由集電極平均電流IC和平均反向電壓VDC決定，可近似如式(3)所示。

(13)

式中：Eon為開通損耗，Eoff為關斷損耗。EswN為額定反向電壓VDCN下開關損耗，為集電極平均電流IC的函數，該函數關系可由器件數據手冊給出。

5 仿真計算原理與結果分析

5.1 直接耦合有限元仿真算法

由于芯片等效電導率的設置，整個仿真模型成為了對于溫度的非線性系統。具體來說，該仿真模型滿足如熱傳導方程式(14)所示。

(14)

式中：λ為材料熱傳導系數；H為發熱功率；ρ為芯片材料密度；c為比熱；T為溫度。其中發熱功率隨溫度的變化而變化，因此整個系統呈現出非線性的特點。由于該非線性偏微分方程顯式解無法直接求得，因此，這里通過迭代法近似求解。原理如下。

首先，設置溫度初值計算得到初始芯片發熱功率H0，同時計算得到溫度T0，再帶入T0計算得到新的發熱功率H1，再利用H1計算得到新的溫度T1，反復迭代i次后，當Ti與Ti-1的差值小于預設殘差后，即認為計算收斂，則Ti就是非線性偏微分方程的近似解，即實際溫度分布。

5.2 仿真結果分析

將4.1節工況參數代入式(4)—(9)可求得器件集電極平均電流IC=623 A。另外，根據4.2節的簡化計算，我們可以看到，當集電極平均電流IC以及反向電壓VDC恒定的情況下，MMC子器件中壓接型IGBT器件的總損耗為結溫Tj的單值函數，并且可由器件數據手冊得到。本文研究對象為某型號壓接型IGBT器件，其輸出特性曲線以及開關能量曲線如圖4所示。讀取IC=623 A時不同溫度下器件飽和壓降以及開關能量，并進行線性擬合，即可分別得到不同溫度下壓接型IGBT器件導通損耗和開關損耗。通過溫度線性擬合，即可得到壓接型IGBT器件損耗與結溫的關系為：

P(T)=1.359T+581.2

(15)

將式(15)代入式(3)并進行相應化簡，可以得到IGBT芯片等效電導率隨溫度變化的函數為：

σ(T)=11 000/(1.359T+581.2)

(16)

設置模型材料電熱屬性如表1所示。

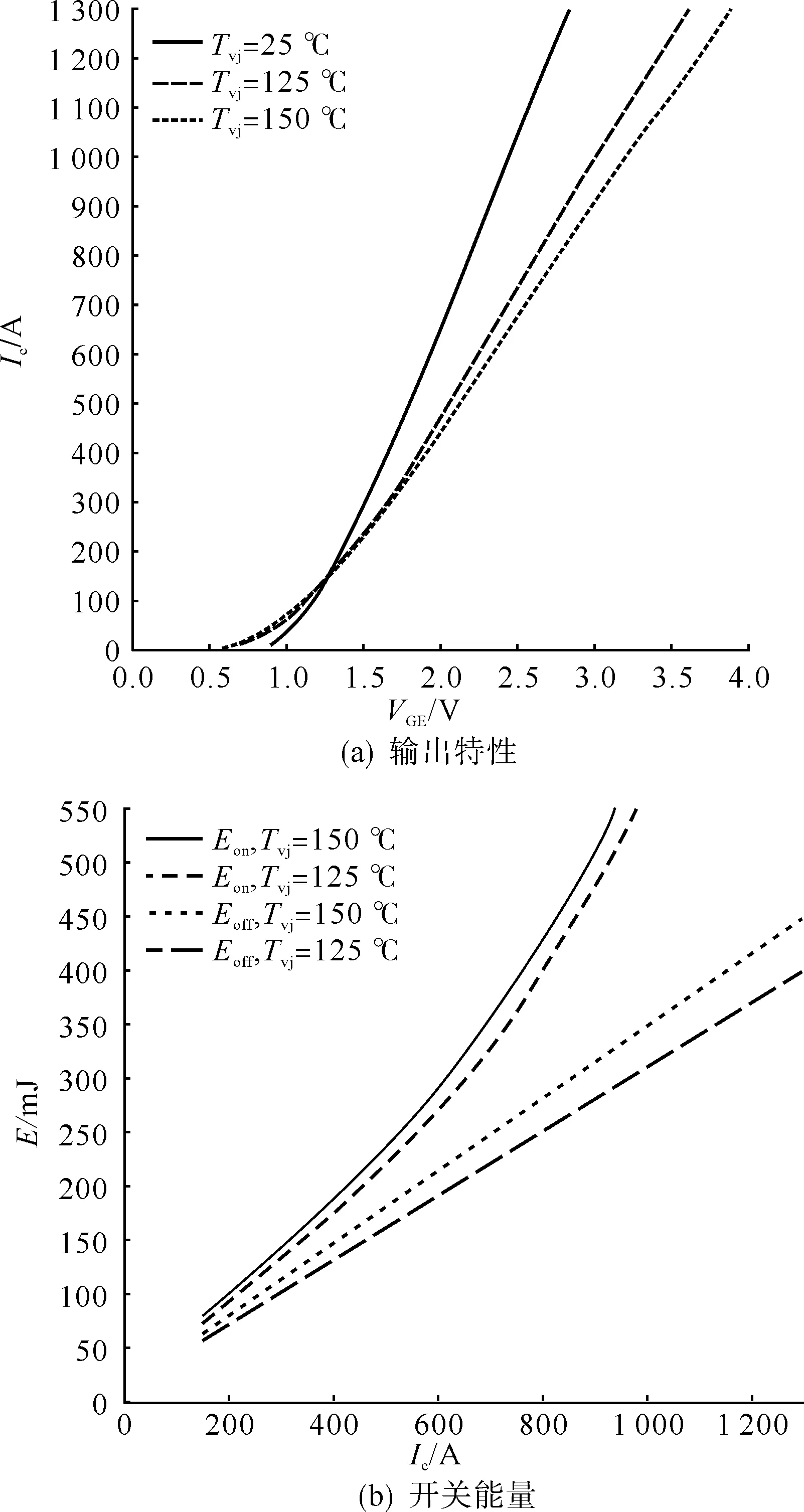
圖4 器件數據手冊曲線Fig.4 Curves of device data sheets

表1 仿真模型材料電熱屬性Tab.1 Electricthermal properties of simulation model materials

設置電流邊界條件為623 A電流從集電極外表面流入，發射極外表面流出。熱邊界條件為集電極和發射極外表面對流換熱系數為1 500 W/(m2·K)，仿真類型為穩態。

仿真經過6次迭代計算，溫度殘差達到0.05%，表明迭代結果收斂，得到溫度分布云圖如圖5所示。

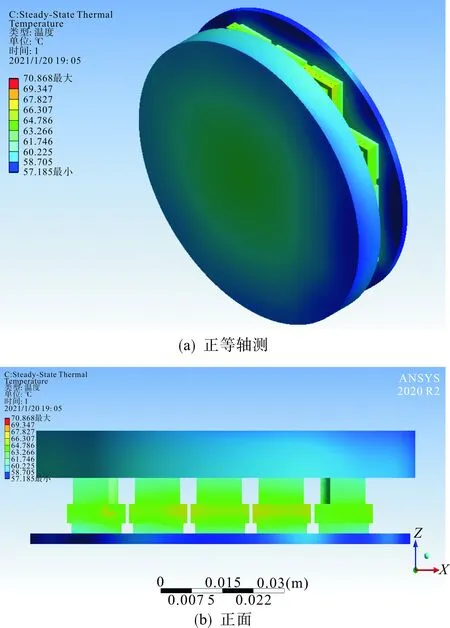
圖5 MMC工況下壓接型IGBT器件溫度分布 Fig.5 Distribution diagram of press-pack IGBT under MMC condition

由圖5可知，壓接型IGBT器件運行時，存在一定溫度梯度。由熱傳導路徑所決定，IGBT芯片溫度較高，兩側凸臺溫度較低。同時，由于各芯片發熱功率和散熱情況存在差異，導致器件中心溫度高于四周。

當IGBT器件工作時，芯片處溫度較高，由于芯片表面存在金屬鍍膜，其在反復的功率循環下會出現裂痕，進而導致器件失效。因此研究IGBT芯片在器件工作時的溫度分布有著重要的意義。

如圖6所示為工況下芯片表面溫度分布。由于電流和溫度分布的不均勻，導致器件內部芯片發熱功率存在差異，最終導致器件內部溫度分布不均勻，其中溫度最高處可以達到70.86 ℃，位于中心芯片邊緣。溫度分布呈現自中心向周圍遞減的特性。由于器件內部多層結構材料熱膨脹系數的不匹配，使得材料連接處產生相對位移的趨勢，導致熱應力的產生，這種趨勢隨著連接處溫度的升高而增大。所以中心芯片在工況下將承受最大的熱應力，最容易出現失效。因此，在子器件閥串散熱器設計中，需要考慮增強器件中心散熱能力，進而實現降低中心芯片溫度，提高子器件運行可靠性的作用。

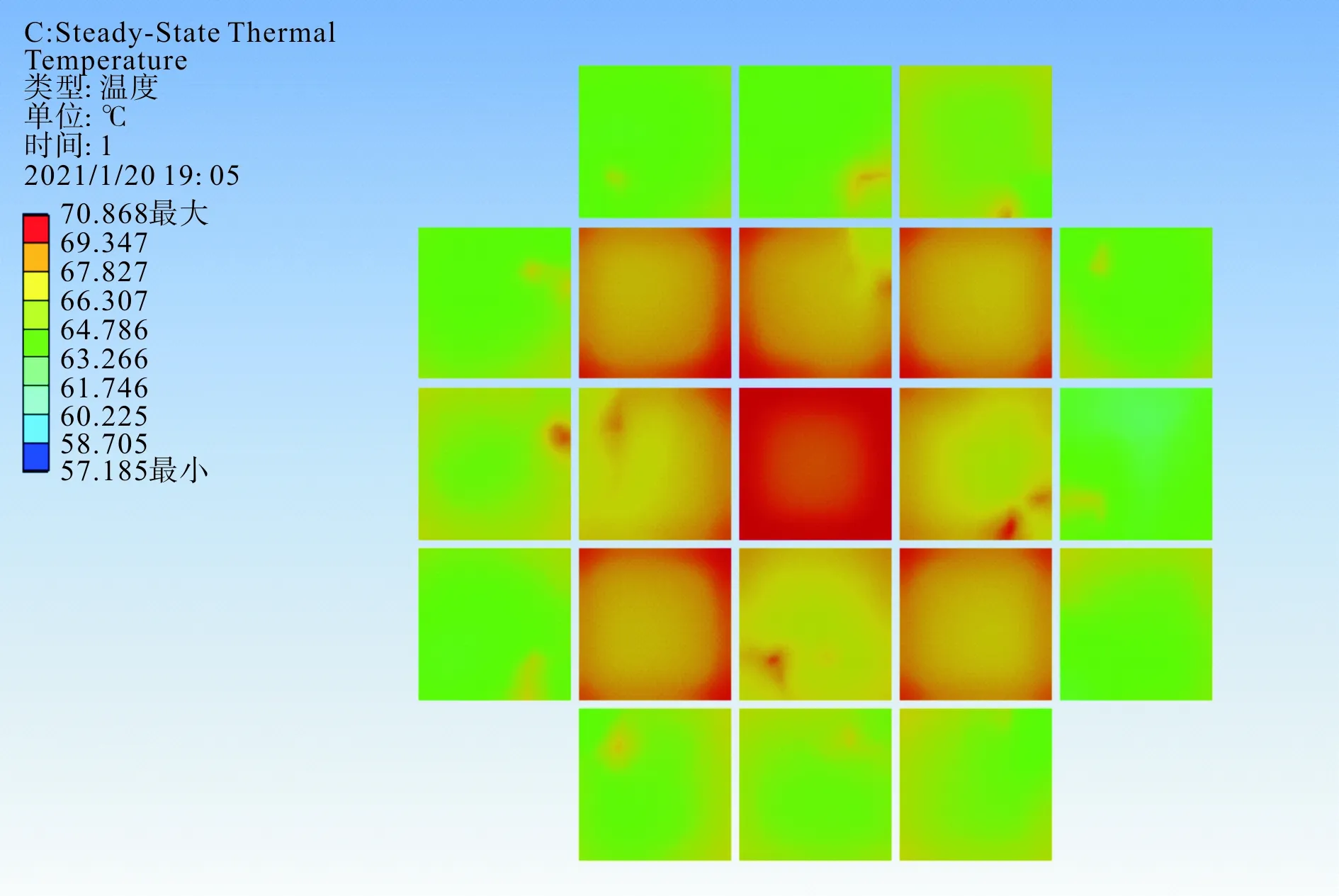
圖6 MMC工況下壓接型IGBT芯片溫度分布Fig.6 Temperature distribution diagram of press-pack IGBT under MMC condition

6 結語

本文研究了基于等效電導率的壓接型IGBT器件芯片損耗建模的方法，通過建立芯片等效電導率與溫度之間的關系，反映了IGBT芯片發熱功率隨溫度變化的特性，進一步體現了壓接型IGBT器件內部由于溫度分布而造成的芯片發熱不均勻，提高了壓接型IGBT器件內部溫度場仿真的準確性。同時，本文在MMC工況下使用該仿真方法進行了溫度場仿真，得到了確定的MMC工況下的壓接型IGBT器件的內部溫度分布規律。該仿真方法對于不同工況具有普適性，因此對于大功率換流器電力電子器件的可靠性分析和壽命預測具有重要意義。