條件概率的本質及其教學建議

李杰民，廖運章

條件概率的本質及其教學建議

李杰民1，2，廖運章1

（1．廣州大學 數學與信息科學學院，廣東 廣州 510006；2．嶺南師范學院 數學與統計學院，廣東 湛江 524048）

概率是一個集合函數，是一種測度，用于度量隨機事件發生的可能性的大小．概率采用公理化定義，條件概率也滿足該定義，因此條件概率也是一種概率測度，條件概率是含參變量的集合函數，是概率的推廣．采用質性研究方法，梳理近20年來高中一線教師撰寫的概率教學文獻，對存在的問題進行分類與歸因，選擇兩篇代表性文獻進行案例研究．研究發現，條件概率概念教學存在較多問題，問題出現的根本原因是一線教師對條件概率本質的理解存在欠缺．條件概率概念教學應當從概念的本質入手，借助正例反例與圖形直觀，講清楚概念的內涵；解題教學應當從數學建模的理念入手，培養解題規范意識，掌握兩種基本計算方法；高中數學要重視條件概率教學，展示概率理論的價值，激發學生學習概率知識的興趣．

高中概率教學；條件概率；概率測度；概率的公理化定義；教學建議

1 問題提出

2003年，教育部印發的《普通高中數學課程標準（實驗）》設置了概率與統計的內容[1]．概率統計進入高中數學課程給一線教師帶來了挑戰[2]．與統計內容相比，概率作為數學的分支，理論性更強．一線教師對抽象度較高的概率理論的理解欠缺[3]，甚至沒有學過概率論[4]，對新增內容的講授經驗缺乏，使得概率教學成為高中數學教學的一個難點，也引發了廣泛關注．使用“百鏈云”圖書館搜索年度范圍限制為2003—2018年，標題中含有“高中”與“概率”的中文學位論文多達100篇，這些論文大部分采用了調查研究法，從不同的側面與視角探討高中概率教學，部分論文對高中數學教師概率基本概念及其認識的狀況進行了調查與訪談，研究結論是大多數教師不了解概率的公理化定義[5]，教師對條件概率、小概率事件的知識非常欠缺[6]．因此，建議加強教師的在職培訓，但文[6]同時指出，“教師培訓沒有起到應有的作用，教師培訓的內容形式不能滿足教師的需要”．

條件概率是概率論中一個基礎而重要的概念，大量的后續概念建立在該概念基礎之上，比如，全概率公式與貝葉斯公式、指數分布與幾何分布的“無記憶性”、假設檢驗中的“兩類錯誤”，等等．條件概率的定義看起來并不復雜，初學者甚至覺得非常簡單，但付諸教學實踐，卻出現各種問題，甚至出現了科學性錯誤，且錯誤存在多年，說明很多教師還不知道錯誤的原因，沒有理解條件概率的本質，沒有找到合適的講授方法．

已有研究缺少對條件概率教學的關注與深入探討．其一，問題本身具有一定的難度．文[7]基于主持“古典概型”公開課活動，發現高中概率模型學與教中存在較多問題．比如，教師在講“古典概型”這一節時，沒有解決“為什么要學習古典概型”“古典概型是什么”這些問題．由此看來，“為什么要學習條件概率”“條件概率是什么”更不容易回答．但文[8]的研究表明，即使是六年級的學生，也具備一定的對高階概率內容如“條件概率”的認知潛能．因此，雖然有難度，但條件概率的教學值得深入研究．其二，條件概率的重要性沒有引起足夠的重視．文[9]通過對兩道有爭議的概率題的調查與分析，認為目前高中概率教學存在著“基本概念的認識較為模糊，普遍輕視基本概念和數學基本思想”的現象．文[9]提到其中的問題1有人采用條件概率的方法，但一筆帶過，其實，從條件概率而不是“等可能性”的角度去分析問題的解法更有針對性．從學科專業角度來看，已有研究忽視了一個重要的事實：復雜隨機現象的深入研究，離不開條件概率這個強有力的工具．從教學法的角度來看，已有研究忽視了一個重要方法：在概念體系中掌握概念[10]．“為什么要學習古典概型”“古典概型是什么”這些問題的解決需要對概率內容有整體的認識，備課時單獨考查“古典概型”是找不到答案的，“古典概型”的教學難點是什么給一線教師造成了困惑[11]也就不足為奇了．只有在概率論的概念體系中比較分析，才能領悟各種概率模型的功能與定位．條件概率既是一種工具，也是一種思想，與各種概率模型均有聯系，研究條件概率的內涵與教學，不但可以為該內容的教學實踐提供參考，從中還可以發現其它概率模型的局限與適用范圍、教學難點等信息．因此，條件概率教學研究的重要性應當引起重視．

具體而言，研究解決這樣一些問題：其一，條件概率的本質是什么？條件概率與概率的關系如何？其二，指出高中條件概率概念講授中存在的問題及其原因，提出改進方法或策略．其三、給出條件概率的教學建議，并以2019年高考數學全國卷Ⅰ壓軸題為例，說明條件概率在概率知識體系中的重要地位，指出高中數學應加強條件概率教學，凸顯其重要性，展示概率理論的價值，激發學生學習概率知識的興趣．

2 研究設計

最近十多年，來自一線教師基于經驗總結或教學反思的條件概率教學文獻逐漸增多，一些老師還介紹了自己的教學案例[12]．為此，研究者嘗試另外一種方式，梳理最近十多年高中教師撰寫的概率教學文獻，傾聽一線教師講述概率教學的故事，了解一線教師對概率基本概念的理解狀況、教學理念與教學設計、解惑方式方法等信息．在研讀大量一線教師文獻的基礎上，將存在的問題進行分類與歸因，指出存在多年但未被教師意識到的錯誤及其深層原因，給出針對性較強的改進建議．

另外，尋找有關教學案例的文獻進行案例研究，希望借助案例，搭建教師自我研究與反思的平臺，創建理論指導實踐的典型實例．案例分析關注如何改進條件概率概念教學，指出已有教學實踐存在的問題，提供“改進版”，供一線教學參考，也可以作為高中教師在職培訓的材料．

研究方法：質性研究方法[13]，具體包括文獻內容分析法和案例分析法．研究材料：高中一線教師發表的概率教學文獻，其中，案例材料來自于文[12]和文[14]．

3 條件概率的本質

高中階段與大學階段給出的條件概率的定義是一致的，概念的表述幾乎完全相同，但對于該概念的解讀與教學卻大不相同．原因在于：大學階段，關于概率的基本概念采用的是演繹推理的方式，即先介紹概率的公理化定義，后給出條件概率的定義，并證明條件概率也是概率，然后由演繹推理自動得到“條件概率具有概率的性質”這一結論，但高中階段沒有介紹概率的公理化定義，而是采用從特殊到一般的歸納推理方式“誘導”出條件概率定義，在介紹完定義后，“強行”指出“條件概率具有概率的一般性質”這一結論[15]．教材內容編排的這種差異給高中一線教師帶來了挑戰，對于培養數學教師的大學數學教育專業的概率統計課程教學而言，是一次與高中內容深度對話的教學契機，然而，多數大學教師并不了解高中教材的細節，對這一重要信息往往一帶而過，或者，雖然了解高中數學教材，但如果意識不到同一內容在不同階段采用不同講授方法的原因，也會錯失重要教學事件的教育價值，結果是大學與高中階段各說各話，銜接不暢，學生不明其中差異，教師沒有捕捉到展示大學概率理論價值的教學時機，十分可惜．

高中階段介紹的“古典定義”“幾何定義”“統計定義”都不是嚴格意義上的定義．如所周知，數學概念的定義非常嚴謹，一般不會出現多個定義，如果出現不同定義，需要證明其等價性．這里所謂的“古典定義”主要是給出“古典概型”的概率計算公式，“幾何定義”主要是給出“幾何概型”的概率計算公式，“統計定義”則是給出概率值的近似計算策略．沒有公理化定義作為前提，高中階段無法進行演繹推理，如何講授條件概率的定義，自然成為一個教學難點，化解該難點，需要合適的教學理論作為指導，也需要較為深厚的專業功底，需要對條件概率的本質具有較為專業的理解．

3.1 概率的公理化定義及其價值

通俗地說，正如小學生用尺子去測量線段的長度，概率是一把用來度量隨機事件的關鍵屬性即“發生的可能性的大小”的“尺子”．需要特別指出的是，概率測度采用公理化定義，滿足該定義的集合函數是不唯一的，比如，條件概率也滿足該定義的3條公理．

概率的公理化定義具有重要意義．首先，從17世紀到20世紀，概率及其相關研究曾經長期游離在數學大家庭之外，有了概率的公理化定義，概率論獲得了嚴格的數學基礎．其次，概率論的公理化，是20世紀數學抽象化的一項碩果，它使概率論這門古老的學科煥發出無限的青春，在理論和應用兩方面都進入了嶄新的發展階段[16]．第三，從概率測度與勒貝格測度的差異來看，勒貝格測度采用構造式定義（從構造勒貝格外測度開始），得到定義后再闡明該測度具有非負性、規范性與可列可加性．但樣本空間不同于“固定的”“靜態的”歐式空間，樣本空間是變化的、動態的、抽象的，構造式定義失去了賴以生長的土壤．可見，公理化方法向概率論學科的滲透，是數學發展的歷史必然，或者說，概率的公理化定義，是理性精神指引下的勝利果實，該成果不僅是歷史功績，也是現代概率論研究的邏輯起點，并具有方法論的啟迪意義．

3.2 條件概率的本質

對于條件概率的本質，可以從不同視角進行解讀，比如應用視角、文化視角，研究者從學科專業知識及其教學的視角，將其本質特征提煉為以下3點．

4 案例分析

4.1 兩個案例

文[14]介紹了高中條件概率概念教學的現狀與思考，案例1摘選自文[14]．文[12]一位高中教師介紹了自己的條件概率教學案例與教學反思，案例2摘選了其中的關鍵教學片斷．

案例1：條件概率概念教學現狀與做法（高中一線教師視角）

第1部分：新增條件概率的背景分析（略）．

第2部分：條件概率的教學現狀．條件概率是整個概率論教學的難點，學生學習條件概率總感覺困難，其原因表現在兩個層面，學的層面（略）．教的層面：（1）由于條件概率在高中數學的地位和高考要求不高，教師不愿意在教學上做過多投入，自身研究得少，教授概念“草草處理”，遇到問題“回頭加工”，教學“功利化”，重結論，輕過程，結果欲速則不達，反而給教學帶來負擔．（2）對條件概率的地位作用認識不足，就概念講概念，沒有認識到條件概率概念的重要性，對概念產生的根源以及概念的內涵、外延不做深入分析，對概念的應用價值挖掘不深，教學“理想化”“走捷徑”．正因如此，高中階段對條件概率的教學表現出3種傾向，一是把其作為過渡性概念處理，……，淺嘗輒止，一帶而過，二是放棄概念教學，直接進入獨立重復試驗教學，三是把符號當作定義，不對概念形成進行深入剖析．

上述諸多因素，造成學生不能理解和掌握條件概率的概念，不能體悟其中蘊含的思想方法，更談不上通過條件概率的教學培養學生的數學能力和素養．

第3部分：條件概率教學的幾點做法．3.1生成概念從情境構思開始……，普通高中數學課標教材，條件概率的概念是通過實例引導學生發現，由特殊到一般，得出3個概率之間的關系，……，整個過程凸顯“從古典概型入手，回歸條件概率本源”的思想．實際教學時，教師覺得意猶未盡，還可以增添其它情境的案例，從不同的角度，強化條件概率的概念形成過程，使得概念的建立更合情合理，更有說服力，因此（將歸納推理的流程在“幾何概型”情境下進行一次），不僅使得概念得以強化，而且以后把條件概率運用于“幾何概型”更顯得自然而然……3.2理解概念從事件分析入手……，條件概率最容易混淆的是兩個事件與|……3.3運用概念在本質解構中把握……

案例2：條件概率教學案例片斷

依照教參“由歸納得出概念”的教學指引，（教師）先給出一個引例，然后嘗試引導學生“發現”條件概率的定義．由于所舉的例子恰好滿足條件()=()，結果引出了兩個等式，始料未及的是，大部分學生贊同采用以下式子作為條件概率的定義：

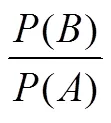
面對這種“出乎意料”的情形，教師化解：“靈機應變”讓學生尋找原因（()=()），找到原因后讓學生更換例子，避免出現()=()．教師認為“矛盾恰到好處地化解了，表現出高超的教學水平”．

4.2 案例分析：概念講授存在的問題與改進策略

人教版選修2-3通過一個“獎券的抽取”問題[15]作為鋪墊，引導出以下式子

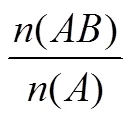
從而歸納出條件概率的定義．這是一種從特殊到一般的推理，給出了定義的緣由，但定義的合理性，“為什么要這樣定義”還需要必要的解讀．作為教師，備課時既要考慮到“有疑”，還要思考如何“釋疑”．

案例1的處理方法：教師覺得意猶未盡，還可以增添其它情境的案例，從不同的角度，強化條件概率的概念形成過程，使得概念的建立更合情合理，更有說服力，因此（將歸納推理的流程在“幾何概型”情境下進行一次），不僅使得概念得以強化，而且以后把條件概率運用于“幾何概型”更顯得自然而然．

案例2的處理方法：引導學生“發現”條件概率的定義，但始料未及，大部分學生贊同另外一個表達式(|)=()/()，于是讓學生尋找原因，更換例子，避免出現()=()．

從案例1可以看出，教師對條件概率概念教學的重要性的分析是比較全面而中肯的．“教的層面”雖然存在教師不重視的主觀原因，但從“高中階段對條件概率的教學表現出3種傾向”來看，一線教師似乎缺少一把“抓手”，或者一個“支點”，不清楚應該“講什么”以及“如何講”，案例1作者的處理方法也驗證了這一點．將歸納推理的流程在“幾何概型”情境下再進行一次，這樣設計是否有利于“釋疑”，值得商榷．教材已經給出了定義的緣由，給出了定義，按照文[10]的觀點，接下來應該是“概念的辨析”，“用概念做判斷”，以及“概念的精致（建立概念間的聯系）”．引導學生再“發現”一次，未嘗不可，但是難以起到辨析的作用，而且對一般情形是否適用，疑問還是沒有消除．

對于一般情形，定義的合理性如何解釋？可以借助文氏圖（圖1）進行直觀性的說明．結合圖1與條件概率的定義，讓學生感悟條件概率是在W的子集上考慮概率運算，即所謂的“縮減樣本空間法”．除了直觀展示，建議再結合反例來“逼近”真相．正好案例2出現了一個反例，遺憾的是，這個預期之外的反例沒有被好好使用．事實上，案例2“更換例子”的做法似乎只是想和書本上的定義保持一致，但即便出現()=()的情形，并不影響條件概率的定義．如所周知，反例列舉一個即可，但從正面證實求是的角度，花時間去尋找一個具體的例子，似乎是一種無奈之舉．

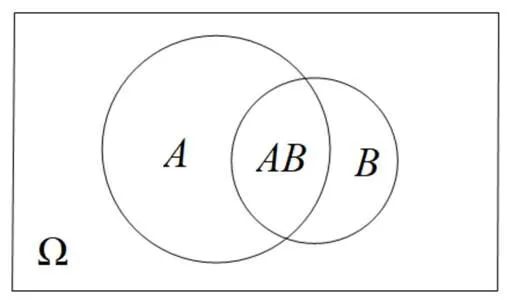
圖1 的情形

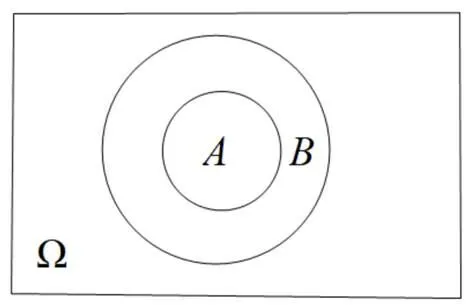
圖2 的情形

情形1：學生意識到(|)=()/()“有毒”，教師繼續引導學生分析，要使得定義式左邊的(|)≤1，則右邊分式的分子應該小于或等于分母，根據概率的單調性，以及常識：右邊式子必須出現變量，分子理應是()，這樣的結局皆大歡喜．經歷了有邏輯的推理，證偽與證實的融合，學生會建立起對定義的理解與認同，深刻記住定義，為之后的應用打下堅實基礎．

情形2：學生質疑為什么要保證(|)≤1，條件概率是概率嗎？這種情形出現的可能性比較小，但難能可貴．此種情形考驗教師的知識儲備，前面關于“條件概率的本質”的分析就可以派上用場，然后又回到情形1．

假如教師不了解條件概率定義的“秘密”，將錯失一次課堂教學的“高潮”．事實上，條件概率的定義，不但保證了(|)≤1，而且保證了“條件概率是概率”．條件概率的本質與定義的科學性往往被一線教師所忽視，概念教學“迷失”了方向，把定義當作公式來演練的現象普遍存在．

證偽使課堂教學更加深刻，但文獻梳理發現，證偽教學案例極少，上述案例2出現反例但擦肩而過[18]．關于證偽教學，喻平指出，一直以來，教學遵循“證實—求是”的范式，只有“存真”而丟失“去偽”，單一的訓練模式會造成學習者的思維定勢，削弱了教學應有的價值；為什么不讓學生體驗尋找真理的艱辛和進入探索問題之門？課程與教學需要檢討和反思[19]．

4.3 案例分析：其它問題及其歸因

（1）把條件概率的定義當作公式來講授．案例1中“條件概率公式的產生過程”很容易讓人誤解，更尷尬的是，大量的文獻把條件概率的定義解讀為公式．此類問題或許與條件概率獨特的定義方式有關，因為給出定義的同時，也給出了計算方法．但是，教師要盡量避免把“定義法”說成“公式法”，雖然對條件概率的計算沒有影響，但是對條件概率的學習與理解會造成阻礙．“公式法”會遮蔽師生的眼光，以致師生不去認真思考定義的緣由、基礎、合理性，荒廢有利于觸及概念本質的教學活動．比如，文[20]不但將“定義法”說成“公式法”，還給出了所謂的“證明”，把定義教成了定理，偏離了概念教學的正確路徑．解決此類問題的關鍵因素是教師對專業概念的理解高度與數學教學觀．

（2）把符號當作定義．文[14]指出，有的老師這樣講授條件概率的定義：設、是樣本空間W中的兩個事件，若()>0，則稱(|)為事件發生的條件下事件發生的條件概率．此類問題并非完全是教師對概念的不重視所致，數學教學心理學中有這樣的描述：概念是反映事物本質屬性的思維形式，概念的命名是表示概念的一種語言形式，比如與概念相聯系的符號．概念的符號與概念緊緊相連，以至于人們常常把符號誤認為概念本身[21]．條件概率的符號(|)直觀形象，容易導致“把符號當作定義”的錯誤．此類錯誤的糾正相對比較容易，比如，可以將概念的表述調整如下．

設、是樣本空間W中的兩個事件，若()>0，則稱()/()為事件發生的條件下事件發生的條件概率，記作(|)．

5 教學建議

5.1 概念教學：從概念的本質入手 借助正例反例與圖形直觀 講清楚概念的內涵

定義不需要證明，但定義的基礎、緣由、合理性等要素需要進行必要的解讀．課程改革已經進入“發展學生學科核心素養為導向”的新時代，建議采用“數學眼光”之“數學抽象”的視角去看待定義的基礎．數學抽象是指通過對數量關系與空間形式的抽象，得到數學研究對象的素養，獲得數學概念和規則是數學抽象的主要表現[24]．條件概率定義用到了“事件的概率”“積事件”“除法”3個前導概念，正是通過對數量關系的抽象得到了條件概率新概念．因此，“數學眼光”有助于發現概念的抽象性，而不是停留在“看上去很簡單”的感性認識層面．按照數學抽象度理論，從“概率”到“條件概率”是一種弱抽象[25]．

人教版選修2-3采用從特殊到一般的推理形式引導出條件概率的定義，屬于歸納推理形式，給出了定義的緣由．教材在介紹完定義后，立即指出“條件概率具有概率的性質”，很多教學論文引用了這句話，至于為什么，幾乎無人提及，事實上，性質是需要證明的．因此，“數學思維”之“邏輯推理”素養融入教學有助于啟發思考，思考“為什么”可能觸發教師對概念本質的領悟，而不僅僅是記住一些結論．比如，性質要一一驗證嗎？或者，只需驗證其中幾個即可？這正是文[26]中問題4的設置意圖．由此可見，條件概率教學是檢驗是否理解概率的公理化定義的試金石．一些文獻[5-6]用“貝特朗悖論”來調查概率的公理化定義的理解狀況是不合適的，出現了因果倒置的邏輯錯誤．可以從概率的公理化定義的視角對“貝特朗悖論”做一些解讀，但作為一道問答題，不能因為被試沒有提及概率的公理化定義就判斷被試不了解概率的公理化定義，因為，“貝特朗悖論”的本質是問題的條件不充分，換言之，問題是一道開放題，把題目補充完整，答案就唯一，補充不同的條件（等可能性假設），就導致不同的解答[27]．

直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化，利用空間形式特別是圖形，理解和解決數學問題的素養，是實現數學抽象的思維基礎[28]．文氏圖雖然是示意圖，但借助圖形直觀有助于條件概率定義的理解，有利于化解教學難點，也有利于發展學生的直觀想象素養．

關于概念教學，需要正例、反例結合使用，引導學生分析定義中的關鍵詞或符號，達到對概念內涵的深度理解．正反例的結合，證實與證偽的融合，使課堂教學更加深刻．

但歸根結底，首先要理解概念的本質，內容決定方法，從概念的本質入手，才能找到合適的講授方法．

5.2 解題教學：從數學建模的理念入手 培養解題規范意識 掌握兩種基本計算方法

關于條件概率的計算，出錯原因主要為兩點，一是“事件符號化”意識淡薄，當出現排列、組合等其它信息干擾時，由于事件含義不明確導致出錯；二是對條件概率的內涵理解不深，不擅長借助圖形直觀輔助解題，以致采用“縮減樣本空間法”解題時常常出現錯誤．

比如，文[29]介紹了這樣一個問題及其解法．問題：投擲骰子兩次，求在第一次擲得的點數為1或2的條件（事件）下，兩次擲得的點數之和為5（事件）的概率．解法一（縮減樣本空間法）：所求概率為=2/6=1/3．解法二（定義法）：()=2/6，()=2/36，因此，(|)=()/()= 1/6．由于兩種方法得出的答案不一致，該文認為解法二錯誤，事實恰好相反，是解法一錯誤．事實上，借助文氏圖（圖3），可以清晰地看出錯誤的原因．

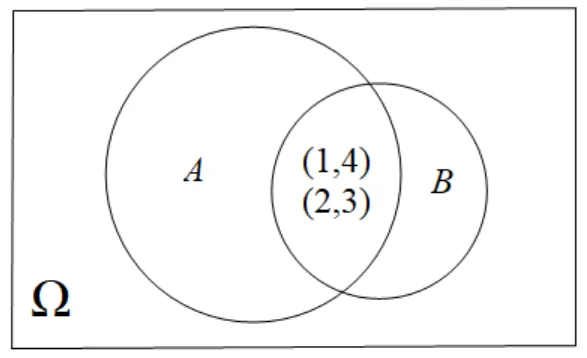
圖3 投擲骰子兩次（只標出兩個事件的交集的元素）

事件表示“第一次投擲骰子的點數為1或2”，因此含有12個元素．文[29]認為拋擲一次骰子有6種結果，故含有6個元素，事實上，該文忘記了前提條件“投擲兩次”，換言之，樣本空間是“2維”的，縮減樣本空間即也必須是“2維”的．在“2維”樣本空間與“1維”樣本空間之間“隨意”切換，導致出錯．事實上，該文的其它問題出現了同樣的錯誤：在不同“維數”的樣本空間之間“自由”的切換而渾然不知．因此，初學者要寫好樣本空間，即使不寫，也要“心中有數”．

因此，關于解題教學，首先，要培養規范意識，按照數學建模的理念來研究解題，牢記問題數學化、事件符號化為第一步．其次，抓住兩種基本方法：“定義法”和“縮減樣本空間法”．需要注意兩點：（1）方法不要“貪多”，有的文獻總結了多種計算方法，淡化方法分類的依據與重要性，得不償失，反而加重了學生的負擔，影響了教學效果．（2）過程不要“貪圖省事”，事件的含義交待不明確往往導致出錯．

5.3 重視條件概率教學 展示概率理論的價值 激發學生學習概率知識的興趣

孤立看待概率模型，缺乏整體認識是目前概率教學存在的誤區．比如，“古典概型”具有“有限”“等可能性”兩個特征，但具有這兩個特征的問題卻不一定適合“古典概型”方法來研究，因為很多問題中的“等可能性”只是一個非本質特征，這正是“古典概型”的教學難點．選擇合適的概率模型有利于問題本質特征的揭示，概率論中很多重要模型依賴于條件概率，比如“無記憶性”模型、“無后效性”模型．

問題1：拋擲一枚硬幣，若出現正面記1分，出現反面記2分，連續拋擲多次，問恰好得到3分的概率為多少？

分析：使用“獨立事件概率乘法公式”和“互斥事件概率加法公式”，得3分的概率為：

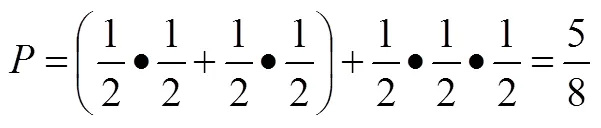
“拋擲硬幣”容易聯想到古典概型，文[30]正是基于“古典概型”探究該問題，得到一種“虛擬解法”．事實上，是一個并未完成的探究，該方法繁瑣且適用范圍窄．比如，文[9]中的問題1（1）與上述問題本質完全相同，只是將拋擲“硬幣”改成拋擲“正四面體”．拋擲一次正四面體，會有4種不同結果，分別對應得到“1分”“2分”“3分”“4分”．要得到4分，拋擲一次、兩次、3次、4次都有可能．拋擲一次，樣本點個數是4個，拋擲兩次，樣本點個數為16個，……，拋擲4次，樣本點個數高達256個，文[30]通過列表“數一數”的“虛擬解法”失去了可行性．

事實上，“等可能性”并非問題1的本質特征，比如，若出現正面的概率是1/3，出現反面的概率是2/3，依舊可以計算概率為：

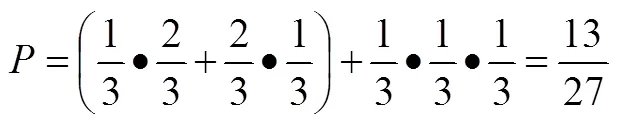
概率值13/27是由3部分組成，對應圖4中的3條路徑，比如，第一步獲得“2分”，然后，第二步獲得“1分”，即0→2→3構成其中的一條得分路徑．更準確的表達是，起始得分為零分的條件下第一步獲得“2分”，然后，第一步獲得“2分”的條件下第二步獲得“1分”，并將對應的概率值做乘法．直覺上很“顯然”的概率（圖4中的分數），其實都是條件概率．

6 結論與展望

6.1 結論

條件概率概念教學存在較多問題，甚至出現了科學性錯誤，問題出現的根本原因是一線教師對條件概率的本質的理解存在欠缺，概念教學缺乏有效的方向指引．在教材已經給出“定義的緣由”的情況下，沒有意識到要講授定義的“基礎”“合理性”“科學性”等概念形成要素，過快地進入“把定義當作公式來演練”的環節，忽視定義的科學性、概念的內涵與價值等要素的有效揭示，從而也不利于數學核心素養的培育．

條件概率概念教學應從概念本質入手，借助正例反例與圖形直觀，講清概念的內涵；解題教學應當從數學建模的理念入手，培養解題規范意識，掌握兩種基本計算方法；高中數學要重視條件概率教學，凸顯其在概率知識體系中的重要地位，展示概率理論的價值，激發學生學習概率知識的興趣．

6.2 展望

條件概率是概率論中一個基礎而重要的概念，在理解概念本質的條件下才能更好地開展教學，否則，會出現各種問題．要理解條件概率的本質，需要熟悉概率的公理化定義及其價值，需要重溫大學概率知識體系，了解概率理論的價值，開闊視野，獲得方法啟迪；大學階段概率教學要研究學生的已有基礎，做好與高中數學的有效銜接與深度對話，如何有效開展，需要進一步研究．

高中概率教學的已有研究，結合一線具體內容的案例研究較少，或者研究結論過于寬泛，成果的可應用性受到制約．這里的研究提供了條件概率這一概率論重要概念的教學案例及其分析，給出了教學建議，希望給一線教師以及高中教師在職培訓提供參考．概率統計核心知識的教學研究，還有很多問題，但專業性很強，難度較大，理論與一線實踐相結合也并非易事，任重道遠，還需繼續努力．

[1] 中華人民共和國教育部．普通高中數學課程標準（實驗）[M]．北京：人民教育出版社，2003：6–7．

[2] 史寧中，王尚志．普通高中數學課程標準（2017年版）解讀[M]．北京：高等教育出版社，2018：191．

[3] 李勇，章建躍，張淑梅，等．全國重點高中數學教師概率統計知識儲備現狀調查[J]．數學通報，2016，55（9）：1–9．

[4] 張蜀青，曹廣福，羅荔齡．從歷史發展的視角看中學概率教學[J]．數學教育學報，2018，27（4）：35–40．

[5] 程伶俐．中學數學教師對概率概念及其教學的認識[D]．上海：華東師范大學，2006：3，7–41．

[6] 冷嬋．高中數學教師對概率統計及其教學認識調查研究[D]．大連：遼寧師范大學，2008：19–32．

[7] 何小亞．高中概率模型學與教中的問題和對策[J]．數學教育學報，2017，26（1）：37–40．

[8] 何聲清．六年級學生對高階概率內容的認知：潛能與局限[J]．數學教育學報，2018，27（3）：57–61．

[9] 謝琳，劉劍濤．從兩個爭議看高中概率論基本概念教學中存在的問題[J]．數學教育學報，2010，19（6）：6–8．

[10] 曹才翰，章建躍．中學數學教學概論[M]．3版．北京：北京師范大學出版社，2012：282–284．

[11] 宮前長．新課程古典概型教學：困惑、解惑與感悟[J]．中學數學（高中版），2014（9）：4–8．

[12] 陳宏杰．“條件概率”的教學案例及教學反思[J]．數學教育研究，2009（2）：25–26．

[13] 陳向明．教育研究方法[M]．北京：教育科學出版社，2013：225–256．

[14] 徐道奎．由條件概率看概念教學在學生素養培養中的重要作用[J]．數學通報，2018，57（6）：34–38．

[15] 人民教育出版社．普通高中數學課程標準實驗教科書·數學（選修2-3，A版）[M]．北京：人民教育出版社，2009：51–53．

[16] 李文林．數學史概論[M]．2版．北京：高等教育出版社，2002：286–292．

[17] 張奠宙，宋乃慶．數學教育概論[M]．3版．北京：高等教育出版社，2016：110．

[18] 頓繼安．數學課堂中教與學“擦肩而過”的現象研究——兼談PCK的利與弊[J]．數學教育學報，2013，22（2）：81–83．

[19] 喻平．教學認識信念研究[M]．北京：科學出版社，2016：239–250．

[20] 金天壽．試談條件概率的教學[J]．數學通報，2012，51（6）：24–27．

[21] 毛鴻翔，季素月．數學教學與學習心理學[M]．沈陽：遼寧教育出版社，1988：80–99．

[22] 韓旭里，謝永欽．概率論與數理統計[M]．修訂版．上海：復旦大學出版社，2009：50．

[23] 石亮．概念與理念齊飛 結論共過程一色——談條件概率的教學[J]．中學數學（高中版），2010（9）：9–13．

[24] 中華人民共和國教育部．普通高中數學課程標準（2017年版）[M]．北京：人民教育出版社，2018：4–5．

[25] 徐利治，張鴻慶．數學抽象度概念與抽象度分析法[J]．數學研究與評論，1985，5（2）：133–140．

[26] 曹廣福，羅荔齡．中學數學部分概率內容的教學策略[J]．數學教育學報，2018，27（5）：17–24．

[27] 張敏，何小亞．貝特朗悖論之爭的終結[J]．數學教育學報，2015，24（3）：51–54．

[28] 史寧中．高中數學課程標準修訂中的關鍵問題[J]．數學教育學報，2018，27（1）：8–10．

[29] 陳武生．一個條件概率問題的辨析[J]．中學數學研究，2018（6）：21–22．

[30] 張紅兵，龔衛東．一個概率問題的解決及其啟示[J]．數學通報，2017，56（5）：21–23．

[31] 李杰民，廖運章．高觀點下一個中學概率問題的分析與啟示[J]．數學通報，2020，59（5）：41–45．

Understanding the Meaning of the Conditional Probability and Its Teaching

LI Jie-min1, 2, LIAO Yun-zhang1

(1. School of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China;2. School of Mathematics and Statistics, Lingnan Normal University, Guangdong Zhanjiang 524048, China)

Probability is a set function; its essence is in measuring the chance of random events. The probability has been defined using axioms, so does conditional probability. Therefore, conditional probability is also a probability measure. Conditional probability is a set function with parameter variables. Using the qualitative research method, the literature on probability teaching written by inservice high school teachers in the past 20 years has been reviewed, the existing problems were classified and attributed, and two representative articles were selected for case study. Based on this research, it was found that there are many problems in the teaching of conditional probability. The rooted problems is that inservice teachers lack their understanding of the concept of conditional probability. Thus, teaching suggestions are as follows: The teaching of the concept should start from the essence of the concept, explaining clearly the connotation of the concept with the help of positive and negative examples and graphic intuition. The teaching of problem solving should start with the concept of mathematical modeling, cultivating the consciousness of problem-solving standardization, and mastery of two basic methods. High school mathematics should attach importance to the teaching of conditional probability, demonstrate the value of probability theory, and stimulate students’ interest in learning probability knowledge.

high school probability teaching; probability measure; conditional probability; the axiomatic definition of probability; teaching suggestions

G632

A

1004–9894（2021）01–0054–07

李杰民，廖運章．條件概率的本質及其教學建議[J]．數學教育學報，2021，30（1）：54-60．

2020–08–10

廣東省高等教育教學改革項目——基于新師范建設的數學教學技能訓練模式和路徑研究（粵教高函〔2018〕180號–458）；嶺南師范學院教育教學研究和改革項目——應用型高校概率統計課程的教學研究與改革實踐（LSJGMS1832）

李杰民（1973—），男，湖南平江人，講師，博士生，主要從事數學教育研究．廖運章為本文通訊作者．

[責任編校：周學智、陳雋]