“中國”“新加坡”“英國”教材中分數除法學習路徑的比較研究

鞏子坤，靳培英，李碩鑫，盧子苓

“中國”“新加坡”“英國”教材中分數除法學習路徑的比較研究

鞏子坤1，靳培英1，2，李碩鑫3，盧子苓4

（1．杭州師范大學 經亨頤教師教育學院，浙江 杭州 311121；2．育才實驗小學，浙江 杭州 311121；3．攝山星城小學，江蘇 南京 210046；4．滕州市龍泉街道安居小學，山東 棗莊 277500）

以中國人教版小學數學教材、英國SMP版小數數學教材和新加坡MC版小學數學教材為研究對象，比較了3國教材中分數除法的學習路徑．結果表明：3國均按照“分數除以整數→整數除以分數→分數除以分數”的順序來安排學習任務；分數除以整數的任務均采用了等分除的模型，整數除以分數、分數除以分數（國內統稱為一個數除以分數）的任務大都采用了包含除模型；任務的表征方式既有直觀表征，也有抽象表征．新加坡教材中的學習路徑所包含的任務最詳細，其推進過程可謂小坡度、慢步走；中國教材的學習路徑所包含的任務最簡略，其推進過程可謂大跨度、快步跑；英國教材的學習任務最為抽象．最后基于分析，重構了分數除法的學習路徑．

分數除法；學習路徑；教材比較；除法模型；表征

1 問題提出

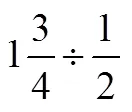
假想學習路徑HLT（hypothetical learning trajectory）首先由Simon在1995年提出[8]．Clements與Sarama在Simon的基礎上，提出了學習路徑的概念：學習路徑就是對學生學習某一具體數學知識時思維與學習過程的描述，以及一個相關的、設想的路徑，這個路徑就是一系列的學習任務[9]．設計（創設）這些教學任務的目的是激發學生心理活動的過程或者行動，促進學生思維水平的發展與提升，達成學習目標．

教材是教與學的重要載體，對教學起著重要的指導作用．研究表明：課程與學生學習成就有正向關系[10]；學習機會絕大部分取決于教師在課堂教學過程中所使用的教材[11]．教材的編寫能否提供最有利于學生理解的學習路徑至關重要．這里試圖從比較研究的視角分析中國、英國、新加坡小學數學教材中呈現的分數除法學習路徑．基于比較分析，提出較為完善的有利于學生理解分數除法算理的學習路徑．

2 研究對象與研究方法

2.1 研究對象

基于影響力與使用范圍的廣泛程度，研究者選取了人民教育出版社發行的小學《義務教育課程標準實驗教科書·數學》[12]（以下簡稱人教版）教材、新加坡Marshall Cavendish出版的[13]（以下簡稱MC版）教材、英國Cambridge University 出版的[14]（以下簡稱SMP版）教材作為研究對象．這些教材都是中國、新加坡和英國所廣泛使用的教材．

2.2 研究方法

學習路徑就是為了達成教學目標而設計的任務序列，這些任務之間具有一定的邏輯遞進關系，這些任務是指向教學目標的[6]．教材中設計的活動或者例子序列，呈現的就是一個學習路徑．因此，這里只對教材中的正文部分呈現的學習路徑進行分析和比較，不涉及后面所附的練習和習題部分．主要從任務系列、模型、表征以及情境這4個維度進行分析．

2.2.1 任務系列

這事實上涉及分數除法的類型．分數除法按照被除數和除數是整數還是分數可細分為以下3種類型：分數除以整數、整數除以分數與分數除以分數．其中分數除以整數的類型又包括分數除以整數（分數的分子能夠被除數整除），單位分數除以整數，分數除以整數（分數的分子不能夠被除數整除）．整數除以分數、分數除以分數（國內統稱為一個數除以分數），包括整數除以單位分數，整數除以分數，單位分數除以分數，分數除以分數．

2.2.2 模型

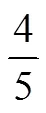
2.2.3 表征

表征指的是說明算理的表示方式，包括以下4類表征方式，即程序表征、直觀表征、抽象表征、形式表征[4]．這4種表征方式的含義如表1[4]．

表1 分數除法的表征類型

2.2.4 情境

世界經濟合作與發展組織（OECD）在國際性學生評價項目PISA中把情境按照與學生生活的遠近分成個人情境、職業情境、社會情境以及科學情境4種類型[16]．在此基礎上，結合文章的需要，增加一個無情境類型作為情境分析框架．各種情境的具體內涵如表2．

表2 情境含義

3 結果與分析

3.1 教材中學習路徑呈現

通過對3國教材中分數除法部分的分析，歸納出教材所呈現的分數除法學習路徑（表3、表4、表5）．

表3 中國人教版教材呈現的分數除法學習路徑

表4 新加坡MC版教材呈現的分數除法學習路徑

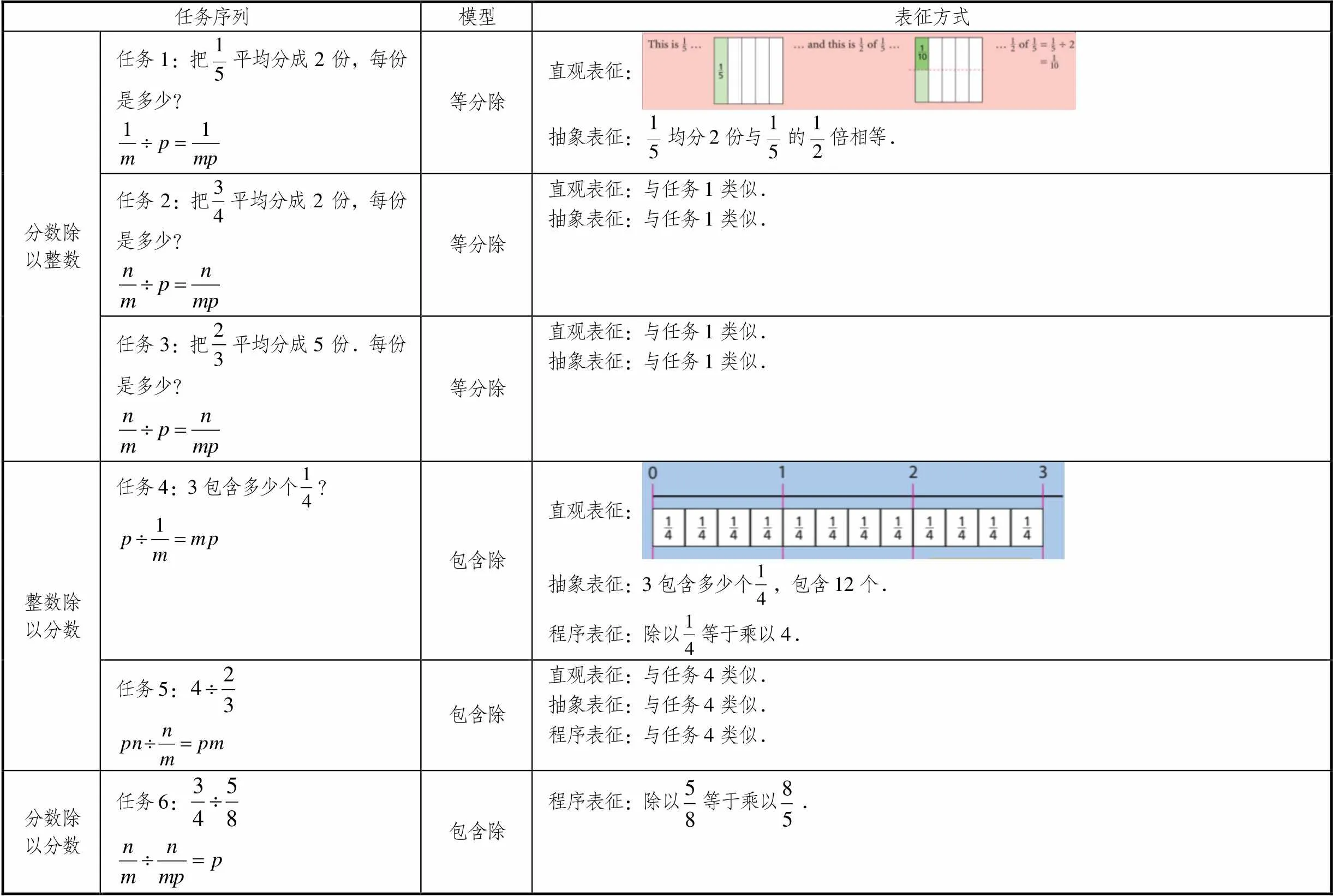
表5 英國SMP版教材呈現的分數除法學習路徑

3.2 學習路徑相同之處

通過比較發現，人教版、MC版、SMP版數學教材中的學習路徑在任務系列、模型、表征、情境方面有相同之處，具體如下．

3.2.1 任務系列

從表3、表4、表5可以看出，分數除法在3國教材中的任務序列基本相同：分數除以整數→整數除以分數→分數除以分數．各國設計的學習任務難度都是螺旋上升的，基本上都是由單位分數除法開始，過渡到可約分的分數除法，最后再到不可約分的分數除法，體現出任務設計的層次性．

3.2.2 模型

分數除以整數，大都使用了除法的等分除模型；整數除以分數，分數除以分數，大都使用了除法的包含除模型．等分除與包含除是由同一個“平均分物”數學模型所產生的，地位平等[16]．從除法的意義進行分析，等分除和包含除，乃是同一個情境里的兩類互相依存的除法問題，可以說二者是一對“孿生兄弟”，彼此密切相關[16]．一個數除以分數，新加坡教材與英國教材多是包含除模型，人教版教材中的任務3、任務4運用了混合模型．

3.2.3 表征

3國教材的分數除法大都用了直觀表征、抽象表征，進而過渡到程序表征．形式化表征則均未出現．在直觀圖的表示上，大都使用了矩形圖，其中人教版還使用了線段圖，MC版還使用了扇形圖．也就是說，除了中國教材外，新加坡、英國教材均使用二維面積模型來表征．

3.2.4 情境

中國教材與新加坡教材設置的任務情境大都是個人生活情境，如均分蛋糕、西瓜、紙張等，教材中設計的每一個學習任務均賦予了實際意義，有著現實的問題情境．學生可以借助這樣的現實情境，用不同的表征方式來理解算理、推導算法，并盡可能實現算理的貫通．英國教材設置的任務只有純粹的數學問題表述，屬于無情境，也就是純數學情境．3國教材設置的任務情境均沒有涉及社會情境和科學情境．

3.3 各國教材呈現的學習路徑的特點

3.3.1 人教版教材：包含除界定不清晰任務推進速度快

（1）注重概括歸納、總結規律．

與其它兩個國家的教材相比較，人教版教材提供的分數除法學習路徑比較注重培養學生的歸納概括能力，如任務后面均呈現這樣的語句“根據上面的折紙實驗和算式你能發現什么規律？”“通過例2、例3的計算，你發現了什么？”，這點明顯區別于其它兩國．

（2）包含除界定不清晰．

人教版教材在一個數除以分數部分運用了混合模型，包含除的形象并不清晰，這給直觀表征算理帶來了不便．

（3）學習任務推進速度較快，增加了教材難度．

人教版教材中所呈現的分數除法學習路徑最短，僅用4個任務就完成了由分數除以整數到分數除以分數整個內容的學習，教材所用篇幅也較少，任務與任務之間的梯度較大，任務1到任務2之間缺乏一個平滑過渡、承上啟下的任務，教材難度較大．

（4）一個數除以分數的任務，結果都是整數．

人教版教材還有一個很大的問題，即整數除以分數、一個數除以分數這兩個任務，所得到的結果均是整數，計算結果極其特殊，不具有一般性．加之這個混合模型的直觀圖也并非真正的直觀圖，線段圖也具有很大的局限性（不能夠一眼看出結果），包含除的形象也不清晰．史寧中先生一再強調：好的結論往往不是先“證出來”的，而是“看出來”的．“看出來”是一種直覺．因而，需要對教材中數字的選取進行改進．

3.3.2 MC版教材：“等分除”“包含除合理運用”任務推進速度緩慢

（1）合理運用等分除、包含除模型．

從對學習路徑模型的分析來看，分數除以整數，使用了等分除模型；整數除以分數以及分數除以分數，使用了包含除模型．對于等分除與包含除這一對“孿生兄弟”，并非厚此薄彼，偏愛一個．

（2）學習任務推進速度緩慢，任務具有同構性．

MC版教材中設計的學習路徑邏輯層次分明，層層漸進地引導學生理解分數除法的算理，逐步提高學生的抽象思維能力．教材提供了大量的篇幅講解一個數除以分數，設置了較多同構性質的任務，每一個學習任務僅在上一個學習任務的基礎上提升一小步，目的是幫助學生逐步理解算理，突破難點．如任務4、任務5、任務6，雖然任務的情境不同，但是，其中的表征方式是一樣的、算理是一樣的、法則也是一樣的．這些任務之間并不是簡單重復，而是對分數除法算理的漸次逼近．它們如登山的階梯一樣，讓攀登者逐步接近山頂，逐步接近算理的真相．

（3）注重“單位”的應用．

“分數單位”與“自然數單位”“小數單位”一樣，是一個比較重要的概念，但在教學中卻容易被忽視．學生經常問老師“兩個分數相除，為什么要用被除數乘以除數的倒數”，若老師講不清楚，學生就只能死記硬背[17-18]，不能促進學生對算理的理解．MC版教材以分數單位作為攀爬的墊腳石，通過直觀圖，引導學生從“分數單位”的意義上去理解“除以一個不為0的數等于乘以這個數的倒數”這一算理，以期逐步達到登頂的效果，如任務1、任務4、任務7．這一點值得大家好好學習．

（4）任務呈現的“不完整性”．

MC版教材中大部分例題有完整的解答過程，但在個別的例題中只呈現了部分解答過程，需要學生自己動手補充完整方框中缺失的數據．所以，MC版教材更能促進學生的思考，進而掌握算理．

3.3.3 SMP教材：拋棄問題情境更加抽象

（1）“無情境”任務成為主流．

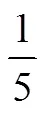
（2）多種方式表征算理．

雖然沒有實際的問題情境，但是SMP版教材通過直觀圖表征從除法的意義、分數的意義以及分數乘法的意義解釋了“除以一個不為0的數等于乘以這個數的倒數”這一算理，如任務1，把其對算理的解釋過程整理如圖1．這是對算理的抽象表征，這種表征方式與人教版教材的表征方式是一致的．而MC版教材沒有出現這種表征方式．

圖1 SMP教材中對分數除法算理的解釋說明

4 分數除法學習路徑：建議與重構

因為各國的國情、數學教育理念、教育的傳統乃至教材編者對數學知識的認識和定位都是不同的，所以各國教材具有不同的特點，出現差異也是很自然的．應該吸取各國教材設計的學習路徑優點，尋求一條最優的分數除法學習路徑．

4.1 建議

學習路徑設計的重點是：設計層次遞進的學習任務，實現算理的多種表征，并貫通各種表征，在講清算理的基礎上水到渠成地推導出法則，從而幫助學生達成對運算的概念性理解與程序性理解[5]．

（1）合理運用等分除與包含除模型．

（2）設計層次遞進的學習任務，平穩過渡，適度推進．

（3）舍棄人教版教材任務3、任務4的混合模型．

4.2 路徑重構

基于以上的分析，提出了假想的分數除法學習路徑，如表6．

表6 假想的分數除法學習路徑

5 結語

通過比較3個國家教材中分數除法的學習路徑，得到假想的學習路徑．研究者將選取實踐學校，開展行動研究，檢驗上述假想學習路徑的有效性；觀察學生的課堂表現，并設計問卷檢查學生對算理的理解；最終以學生理解水平的提升程度、學生課堂表現以及課后訪談作為依據來驗證假想的學習路徑有效程度．

[1] BEHR M, POST T. Rational number, rationed proportion and decimal concepts teaching [M] // Handbook of research on mathematics teaching and learning. Boston: Allyn and Bacon, 1992: 296–333.

[2] 中華人民共和國教育部．全日制義務教育數學課程標準（2011年版）[M]．北京：北京師范大學出版社，2012：46．

[3] 馬立平．小學數學的掌握與教學[M]．上海：華東師范大學出版社，2008：52–70．

[4] 鞏子坤．程序性知識教與學研究[M]．南寧：廣西教育出版社，2010：64–128．

[5] 鞏子坤．程序性知識例規教學模式構建研究[J]．上海教育科研，2016（8）：50–54．

[6] 鞏子坤，朱賢梅，呂婷，等．算理理解視角下的小數乘整數學習路徑[J]．小學數學教師，2017（11）：73–79．

[7] 鞏子坤，俞飛丹，張東，等．程序性知識視角下的小數乘小數學習路徑[J]．小學數學教師，2017（12）：63–67．

[8] SIMON M A. Reconstructing mathematics pedagogy from a constructivist perspective [J]. Journal for Research in Mathematics Education, 1995 (26): 114–145.

[9] ClEMENT D, SARAMA J. Learning trajectories in mathematics education [J]. Mathematical Thinking and Learning, 2004 (6): 81–89.

[10] SCHMIDT W H, MCKNIGHT C C, HOUANG R T, et al. Why schools matter: A cross-national comparison of curricular and learning [M]. San Francisco: Jassy-Bass, 2001: 28–59.

[11] ?HAGGARTY L, PEPIN B. An investigation of mathematics textbooks and their use in English, French and German classroom: Who gets an opportunity to learn what [J]. British Educational Research Journal, 2002, 28 (4): 567–590.

[12] 盧江，楊剛．義務教育課程標準實驗教科書小學數學（六年級下冊）[M]．北京：人民教育出版社，2006：28–32．

[13] ?FONG H K, GAN K S, CHELVI R. My pals are here! Maths pupil’s book [M]. British: Marshall Cavendish Education, 2011: 102–111.

[14] The School Mathematics Project. SMP interact: Foundation 2 [M]. Cambridge: Cambridge University Press, 2007: 25–31.

[15] 張奠宙．教材編寫要注意防止片面的思維定式——評小學數學教材中忽視“包含除”的傾向[J]．小學數學教師，2015（9）：4–6．

[16] ?OECD. PISA 2015 assessment and analytical framework: Mathematics, reading, science, problem solving and financial literacy [EB/OL]. (2017–05–03) [2019–10–10]. https://read.oecd-ilibrary.org/education/pisa-2015-assessment-and- analytical-framework_9789264281 820-en.

[17] 唐德發．分數單位在分數教學中的作用[J]．云南教育，1982（7）：34–35．

[18] 鞏子坤．基于學生的理解水平制定課程目標[J]．數學教育學報，2010，19（2）：34–37．

A Comparative Study on the Learning Trajectories of Division with Fractions in Textbooks from China, Singapore and the UK

GONG Zi-kun1, JIN Pei-ying1, 2, LI Shuo-xin3, LU Zi-ling4

(1. School of Teacher Education, Hangzhou Normal University, Zhejiang Hangzhou 311121, China;2. Yucai Experimental Primary School, Zhejiang Hangzhou 311121, China;3. Sheshan Xingcheng Primary School, Jiangsu Nanjing 210046, China;4. Tengzhou Anju Primary School, Shandong Zaozhuang 277500, China)

In this paper, we compare the learning trajectories of the division of fractions in Chinese elementary school mathematics textbooks, the British SMP school mathematics textbooks, and the Singaporean MC primary school mathematics textbooks. We found that the learning tasks are arranged in the order of “dividing a fraction by a whole number?dividing a whole number by a fraction?dividing a fraction by a fraction.” The tasks of dividing a fraction by a whole number all adopt the portative models, and the tasks of dividing a whole number by a fraction and dividing a fraction by a fraction (generally referred to as dividing a number by a fraction in China) mostly adopt the quotitive models. The representations of tasks included both visual and abstract representations. The learning trajectories in the Singaporean textbooks contain the most detailed tasks, which could be described as proceeding in small steps and at a slow pace. The Chinese textbooks contain the lowest number of tasks, which could be described as proceeding in big steps and at a fast pace. The British textbooks contain the most abstract tasks because they were all purely mathematical situations. Based on these analyses, we propose the hypothetical learning trajectories of the division of fractions.

division of fractions; learning trajectories; textbook comparison; models of division; representation

G40–059.3

A

1004–9894（2021）01–0079–06

鞏子坤，靳培英，李碩鑫，等．“中國”“新加坡”“英國”教材中分數除法學習路徑的比較研究[J]．數學教育學報，2021，30（1）：79-84．

2020–09–30

教育部人文社會科學研究規劃基金項目——6~15歲兒童的概率概念認知策略及其發展研究（15YJA880020）；浙江省哲學社會科學規劃重點課題——兒童的概率概念認知策略及其發展研究（16NDJC004Z）

鞏子坤（1966—），男，山東滕州人，教授，主要從事數學課程與教學研究．

[責任編校：周學智、陳漢君]