旋轉(zhuǎn)機器人手臂奇異位形分析
費 雄,張 宇,孫偉棟
(昆明理工大學(xué)機電工程學(xué)院,云南昆明 650500)
0 引言
近年來,機器人技術(shù)發(fā)展日新月異,在工業(yè)等許多領(lǐng)域都發(fā)揮著不可替代的作用,人們對機器人機構(gòu)問題的研究也越來越深入。對于任何機器人機構(gòu)而言,都會存在一種非常特殊的位姿形態(tài),即機構(gòu)的奇異位形。從機構(gòu)發(fā)明之初,奇異性問題就已隨之而來。機械臂可能會發(fā)生奇異位形的情況大致可分為以下兩種:機械臂工作空間內(nèi)部奇異位形與機械臂工作空間邊界奇異位形[1]。當(dāng)工作空間內(nèi)部發(fā)生奇異位形時,會導(dǎo)致機器人靈活性變差,瞬時喪失應(yīng)有的自由度,無法進行運動,引起機構(gòu)鎖死,可能導(dǎo)致失控的問題,這種情形一般是由兩個或兩個以上關(guān)節(jié)軸線共線引起的;當(dāng)工作空間邊界發(fā)生奇異位形時,機械臂、機械手各個關(guān)節(jié)一般都處于完全伸展開來的形態(tài),或處于與先前相反,即完全收回的形態(tài),這兩種形態(tài)都會使機械臂末端執(zhí)行器處在一個十分接近機械臂工作空間邊界的極限位置形態(tài)。針對這種情況,通常只需機構(gòu)在運動過程中,盡量避免接近該工作空間的極限位置,即可規(guī)避此類奇異位形的發(fā)生。因此,針對機器人機構(gòu)奇異性問題開展相關(guān)研究是非常必要的,對于提升機器人工作性能以及規(guī)避故障可提供重要的理論根據(jù)。
對于機械臂而言,奇異位形是機械臂一種十分特殊的運動特性[2]。針對機器人機械臂的奇異性問題,國內(nèi)外學(xué)者進行了許多理論研究。現(xiàn)階段關(guān)于機械臂奇異性問題的相關(guān)研究理論主要有以下幾種:線幾何理論[3-4]、旋量理論[5]以及代數(shù)理論[6]。劉滿德等[7]最早對機器人奇異性問題展開研究,并引進雅克比矩陣的奇異魯棒逆在奇異點周圍提供可行、連續(xù)的解;胡準慶等[8]針對機器人奇異問題,對形態(tài)各異、類別不同的幾種機器人進行對比研究,從而獲得更精確的數(shù)據(jù)結(jié)果;李誠等[9]運用微分變換方法,以某款膠裝機器人為研究對象,分析求解該機器人對應(yīng)的雅克比矩陣,并以此數(shù)學(xué)矩陣為基礎(chǔ)對該機器人進行對應(yīng)的奇異性分析,從而獲得該膠裝機器人在工作過程中所有可能會出現(xiàn)奇異位形的情況;張新等[10]以一款反恐排爆功能機器人的5 自由度機械臂作為研究對象,分析獲取該機械臂對應(yīng)的雅克比矩陣,并對該機械臂奇異問題進行分析;CHENG 等[11]則對一款具有6 個自由度的PUMA 類型機器人進行奇異性問題研究,并求得該機器人的奇異構(gòu)型情況;NOKLEBY[12]針對某款具有7 個自由度的加拿大臂進行奇異問題分析,同樣也獲得了該機械臂的所有奇異構(gòu)型情況;史士財?shù)龋?3]以某款具有7 自由度的機械手臂作為研究對象,采用旋量抑制方法對該機械手臂進行分析,進而求出與該機械手臂相關(guān)的幾何特征及可能出現(xiàn)的奇異形態(tài);BOHIGAS 等[14]提出一種基于數(shù)值計算的分析方法對并聯(lián)機構(gòu)及平面連桿進行奇異問題分析。
本文首先對傳統(tǒng)機構(gòu)運動模型創(chuàng)建方法進行分析研究,然后對傳統(tǒng)四元素D-H 參數(shù)通用法進行改進,運用改良后的五參數(shù)D-H 方法[15-16]針對旋轉(zhuǎn)機器人機械臂建立對應(yīng)的連桿坐標(biāo)系,以及相應(yīng)的運動學(xué)模型,從而求得對應(yīng)的正逆解,并進行仿真與驗證工作。在雅克比矩陣求解方面,本文在傳統(tǒng)矢量積分法基礎(chǔ)上同時運用微分變換法,兩種方法相輔相成,大大節(jié)省了計算時間,十分方便、快捷。
1 運動建模與分析
本文主要以項目小組自行生產(chǎn)的某一款旋轉(zhuǎn)機器人的機械手臂作為研究對象。該旋轉(zhuǎn)機器人機械手臂整體工作結(jié)構(gòu)以及工作平臺如圖1 所示。

Fig.1 Rotating robot arm圖1 旋轉(zhuǎn)機器人機械手臂
根據(jù)機器人機械手臂所對應(yīng)的D-H 參數(shù),可建立與該機械臂對應(yīng)的坐標(biāo)系圖,如圖2 所示。
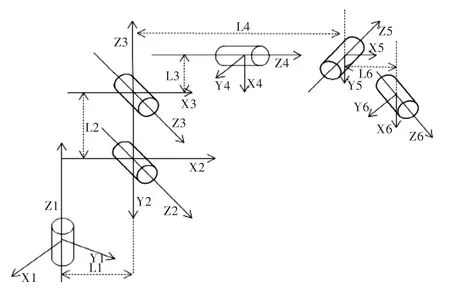
Fig.2 Rotating robot arm coordinate distribution圖2 旋轉(zhuǎn)機械臂坐標(biāo)分布
旋轉(zhuǎn)機器人機械手臂各連桿幾何參數(shù),以及各個關(guān)節(jié)之間對應(yīng)角度等相關(guān)數(shù)據(jù)如表1 所示。
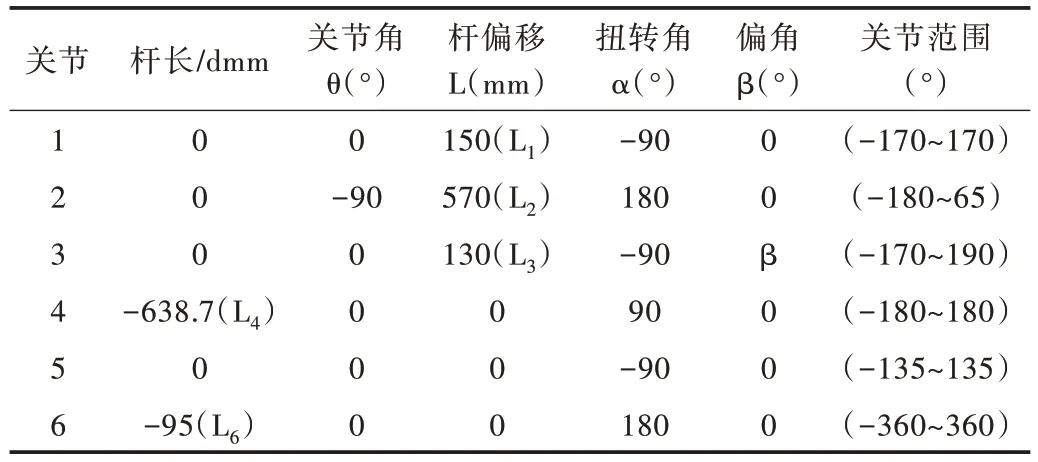
Table 1 Rotating robot manipulator related D-H parameters表1 旋轉(zhuǎn)機器人機械手臂相關(guān)D-H 參數(shù)
根據(jù)上述機械手臂相關(guān)參數(shù),可求得旋轉(zhuǎn)機械臂各連桿變換矩陣如下:

由于機械臂末端執(zhí)行器相對第i 連桿的位姿矩陣是已知的,如式(1)所示。
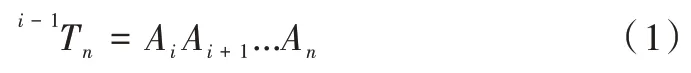
根據(jù)上述公式,可求得旋轉(zhuǎn)機械臂末端執(zhí)行器的位姿矩陣,如式(2)所示。
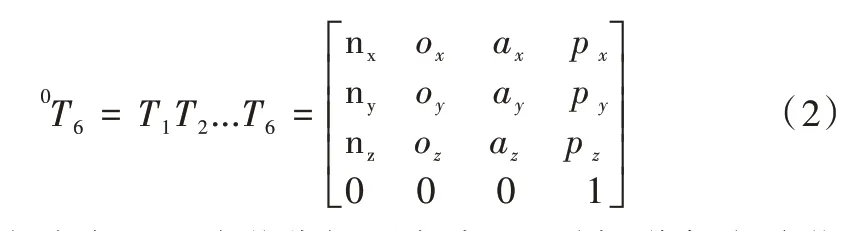
在機械手臂正運動學(xué)分析研究中,只需知道各個關(guān)節(jié)角度,再根據(jù)上述D-H 參數(shù)表中的相關(guān)參數(shù),即可求出機械手臂末端位置及姿態(tài)。而且,對于同一個末端姿態(tài)點,也許是由不同關(guān)節(jié)組合而成的,具有多對單的映射關(guān)系,因此對機械臂進行正運動學(xué)分析會相對容易。因此,可利用MATLAB 分析軟件的輔助模塊ROBOT TOOLBOX,針對該旋轉(zhuǎn)機器人機械手臂樣機搭建數(shù)學(xué)模型[17],并以該模型為基礎(chǔ)進行正運動學(xué)模擬仿真。該旋轉(zhuǎn)機器人機械手臂仿真模型如圖3 所示。
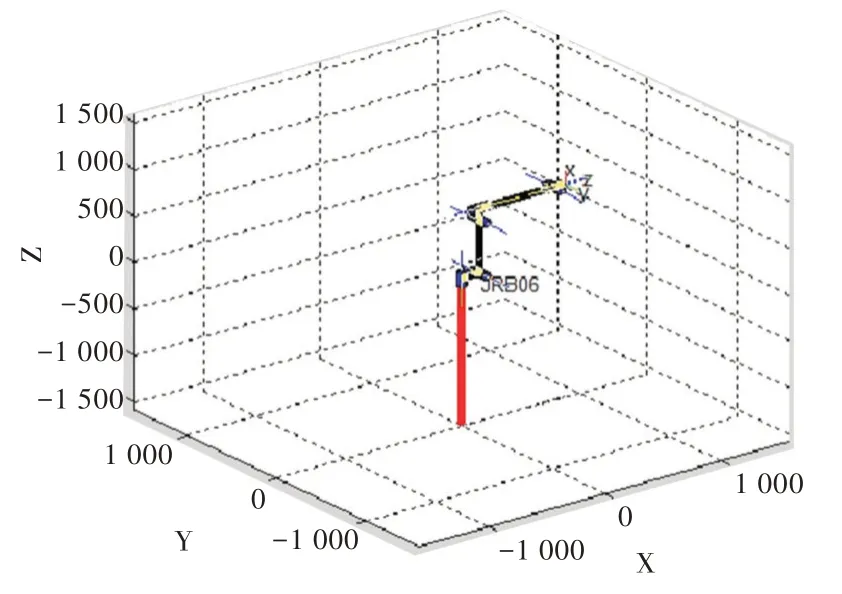
Fig.3 Robotic arm simulation model圖3 機械手臂仿真模型
運用MATLAB 仿真軟件對旋轉(zhuǎn)機器人機械手臂進行模型搭建,并對模型進行仿真分析,以及進行相應(yīng)的正運動學(xué)求解[18]。仿真分析結(jié)果如圖4 所示。
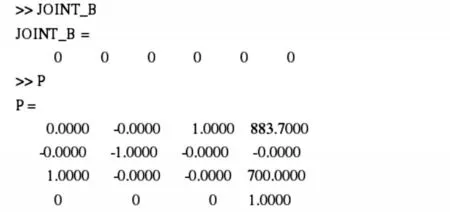
Fig.4 Simulation analysis results圖4 仿真分析結(jié)果
其中,JOINT_B 表示各關(guān)節(jié)初始值,而P 表示初始JOINT_B 對應(yīng)的機械臂末端位姿,以便于后續(xù)分析工作。
2 機械臂雅克比矩陣求取
對于旋轉(zhuǎn)機器人機械手臂雅克比矩陣的求解,可選擇簡潔明了的矢量積法[20],具體計算方式如式(3)所示。
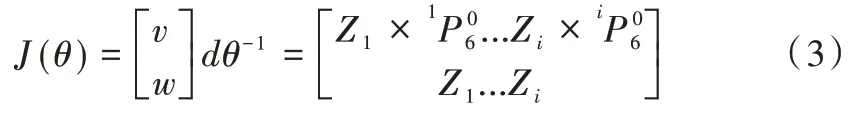
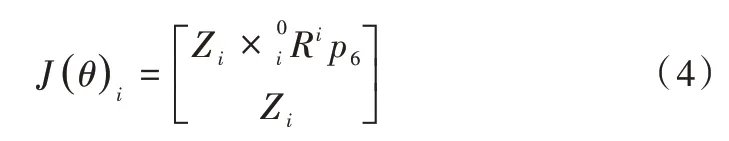
根據(jù)以上關(guān)系式,可變換解析得到機械手臂的雅可比矩陣表示式,如式(5)所示。
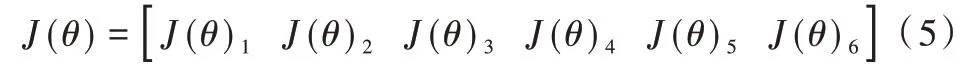
若想運用以上公式求取雅可比矩陣,需依次求出Zi、。矢量積法分別從角速度與平移速度兩方面進行求解,其在表達方面非常清晰明了,且通俗易懂,便于后續(xù)求解。
機械臂的雅克比矩陣是機械臂關(guān)節(jié)速度與末端笛卡爾速度微分運動之間關(guān)系的一種數(shù)學(xué)表達,若更深入研究,則可解釋為機械手關(guān)節(jié)基坐標(biāo)系與尾端坐標(biāo)系兩者之間的微小動作關(guān)系,故可利用微分變換法[21-22]解析其之間的運動關(guān)系。基坐標(biāo)系的細微運動引起末端位姿變化dT,即:
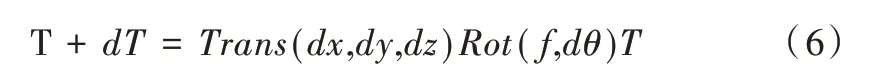
上述公式可通過數(shù)學(xué)變換,變形如式(7)所示。
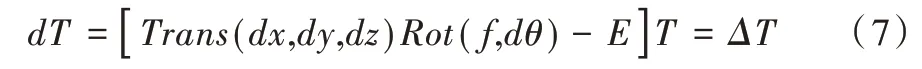
式中,dx、dy、dz 分別表示沿各坐標(biāo)軸的平移量,dθ表示旋轉(zhuǎn)角度,f 表示旋轉(zhuǎn)軸矢量,然后將其代入相關(guān)公式中,可得:
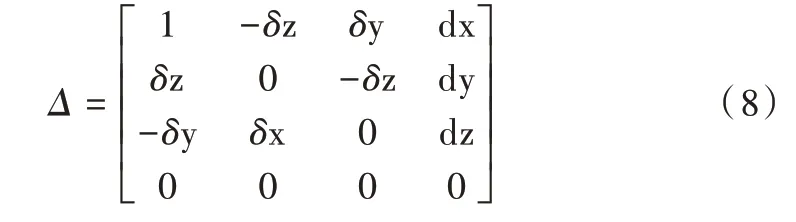
其中,有:
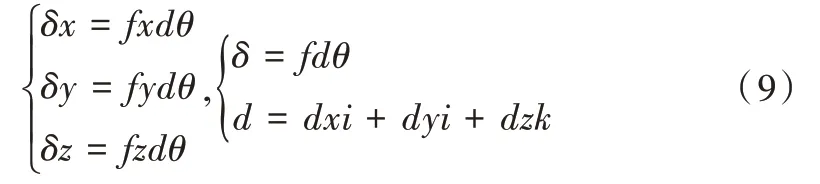
假如機械臂末端坐標(biāo)系有微小變化,可設(shè)機械臂末端位姿變化為TdT,即:
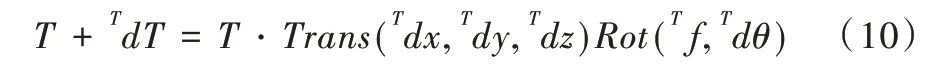
可將以上公式整理變換得到式(11)。
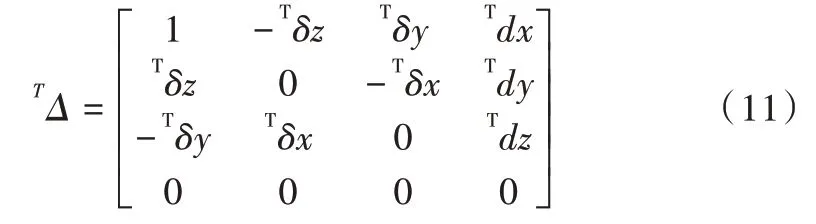
根據(jù)式(8)與式(11)可知同一位姿變化,則機械臂對應(yīng)基坐標(biāo)與末端坐標(biāo)兩者之間的微分運動是等價的,因此有對應(yīng)關(guān)系式dT=TdT。代入相關(guān)公式,可得式(12)。
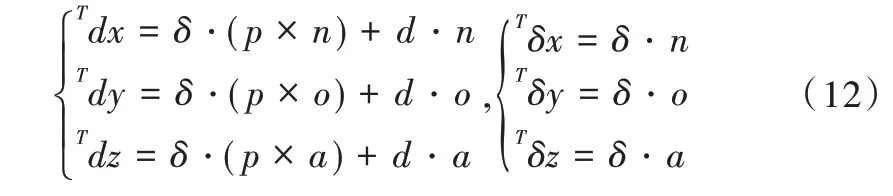
在運用D-H 法搭建的對應(yīng)坐標(biāo)系中,Z 軸方向表示關(guān)節(jié)軸線f 的方向。因此,對于機械臂的轉(zhuǎn)動關(guān)節(jié)i,有旋轉(zhuǎn)量δi=[0 0 1]Tdθi,平移量Td=[0 0 0]T。對于平移關(guān)節(jié)j,有δi=[0 0 1]Tdθi,δj=[0 0 0 ]。代入式(12)即可得連桿到末端坐標(biāo)平移變換與末端坐標(biāo)旋轉(zhuǎn)的雅克比矩陣列矢量表達公式:
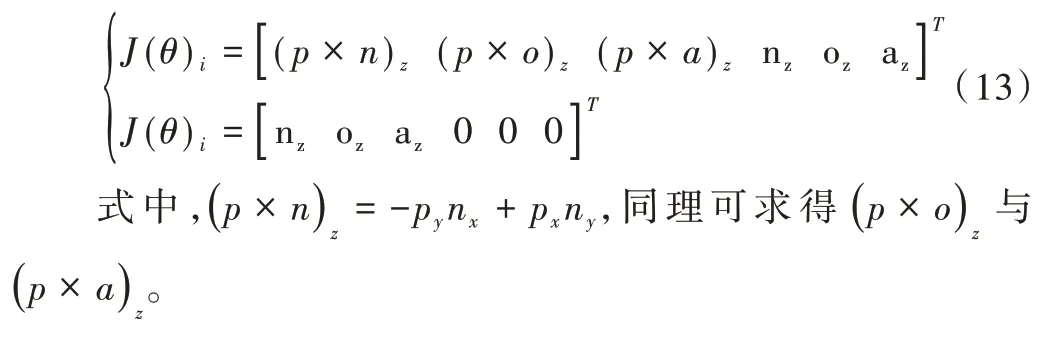
利用式(11)可求出最后一個關(guān)節(jié)的雅克比列矢量,與之對應(yīng)的變換矩陣為:
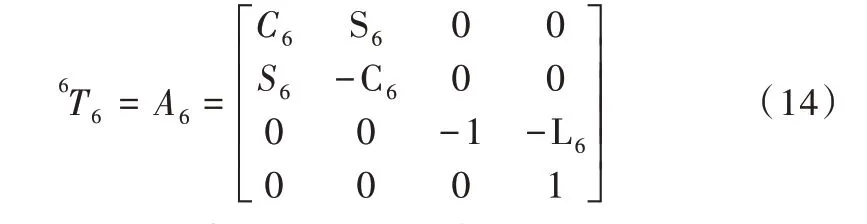
然后分別將對應(yīng)參數(shù)n、o、a、p 代入關(guān)系式,即可解析出相應(yīng)的雅克比矩陣列矢量:J6=[0 0 0 0 0 -1]T。
對于5 號關(guān)節(jié),可在A6基礎(chǔ)上求得其對應(yīng)變換矩陣表示式為:

由于格式限制,機械手臂1 號關(guān)節(jié)與2 號關(guān)節(jié)的列矢量結(jié)果不便于在文中展示,其求取方法同上,故也可求出其雅克比矩陣表達式為:
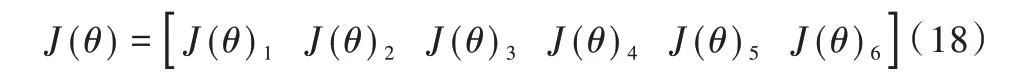
3 奇異位形識別及仿真
雖然各類機器人與機械手臂的形態(tài)構(gòu)型各異,但機械手臂每一個關(guān)節(jié)都有其對應(yīng)運動區(qū)間,以及有效的工作邊界與范圍。因此,在這些極限邊界范圍處即可能產(chǎn)生關(guān)節(jié)的運動極限位姿,即奇異位形。此次試驗的旋轉(zhuǎn)機器人各個關(guān)節(jié)有效運動范圍如表1 所示。
因此,當(dāng)機械臂對應(yīng)關(guān)節(jié)處于θ1=±170°、θ2=180°/65°、θ3=-170°/190°、θ4=±180°、θ5=±135°、θ6=±360°這些極限角度時,此時對應(yīng)點應(yīng)為極限位置奇異點。對于每一個奇異點,可利用MATLAB 并采用ROBOT TOOLBOX工具箱進行機械臂的三維圖形仿真分析。各關(guān)節(jié)在極限位置的三維仿真圖如圖5-圖10 所示。
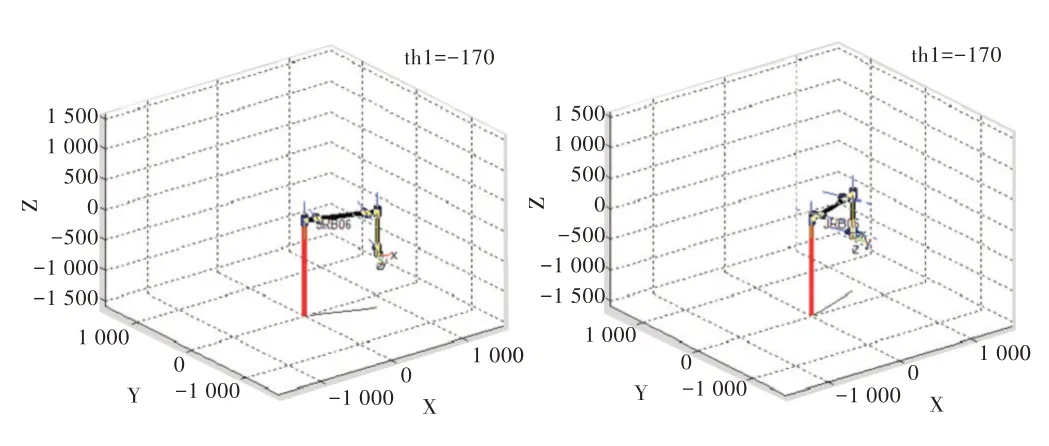
Fig.5 No.1 joint limit position圖5 關(guān)節(jié)1 極限位置
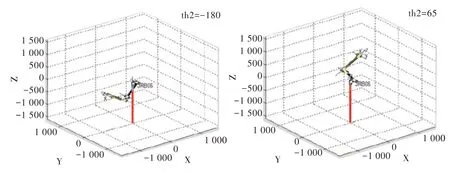
Fig.6 No.2 joint limit position圖6 關(guān)節(jié)2 極限位置
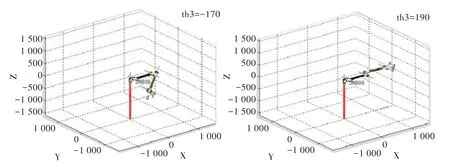
Fig.7 No.3 joint limit position圖7 關(guān)節(jié)3 極限位置
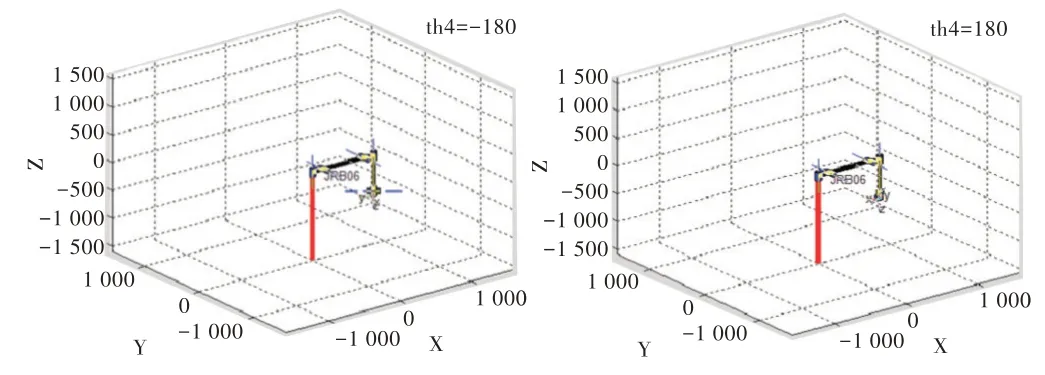
Fig.8 No.4 joint limit position圖8 關(guān)節(jié)4 極限位置
對于第二種奇異位形情況,即工作空間內(nèi)部奇異,由于奇異點根據(jù)雅克比矩陣的逆運動學(xué)求解會出現(xiàn)失效情況,因此可根據(jù)雅克比矩陣對內(nèi)部奇異進行分析求解。由先前求得的雅克比矩陣表達式對旋轉(zhuǎn)機器人可能存在的內(nèi)部奇異位姿進行求解,最后運用MATLAB 對相應(yīng)奇異位姿進行仿真得出三維圖形。
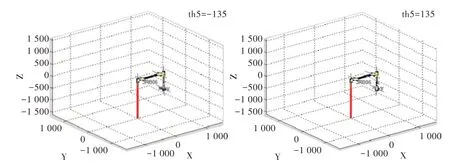
Fig.9 No.5 joint limit position圖9 關(guān)節(jié)5 極限位置
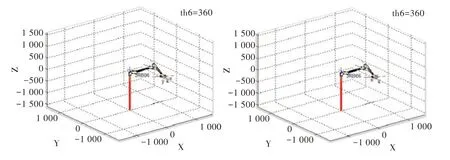
Fig.10 No.6 joint limit position圖10 關(guān)節(jié)6 極限位置
由所得的雅克比矩陣關(guān)系式計算該矩陣行列式det(J(θ)),如式(19)所示。
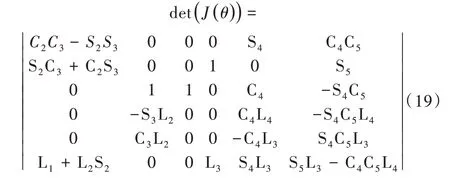
對公式進行行列式化簡,并令行列式等于零,變換結(jié)果如下:
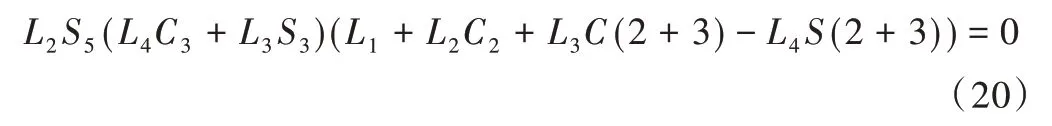
因為L2、L3、L4為機器人機械手臂機構(gòu)所給定的連桿長度,或連桿偏移量不為零,所以假如需要上式等于零的條件成立,則可能有以下3 類情形,具體如下:
(1)當(dāng)S5=0,也即sinθ5=0,此時θ5=kπ,則可知在5 號關(guān)節(jié)角度等于0 時,該機械臂機構(gòu)會出現(xiàn)腕部的奇異情形(-2.356 2 ≤θ5≤2.356 2)。此時,可運用MATLAB 的機器人工具箱對該位置進行仿真分析,如圖11 所示。
當(dāng)5 號關(guān)節(jié)角為0 時,4、6 號關(guān)節(jié)軸線共線奇異如圖12 所示。
(2)當(dāng)L4C3+L3S3=0 時,在這種情形下,可對該公式進 行 變 換 得sin(θ3+β)=0,求 出θ3=arctan(L4L3),其中L3不為零。由于L3=130,L4=638.7,代入公式可得θ3=1.370 0。將相關(guān)參數(shù)代入雅可比矩陣,利用SDV 算法對矩陣進行奇異值分解(采樣點為60 個點),最后求出3 號關(guān)節(jié)角與雅可比矩陣最小奇異值的關(guān)系,如圖13 所示。運用MATLAB 的機器人工具箱對該處的奇異形態(tài)進行模擬分析,如圖14、圖15 所示。
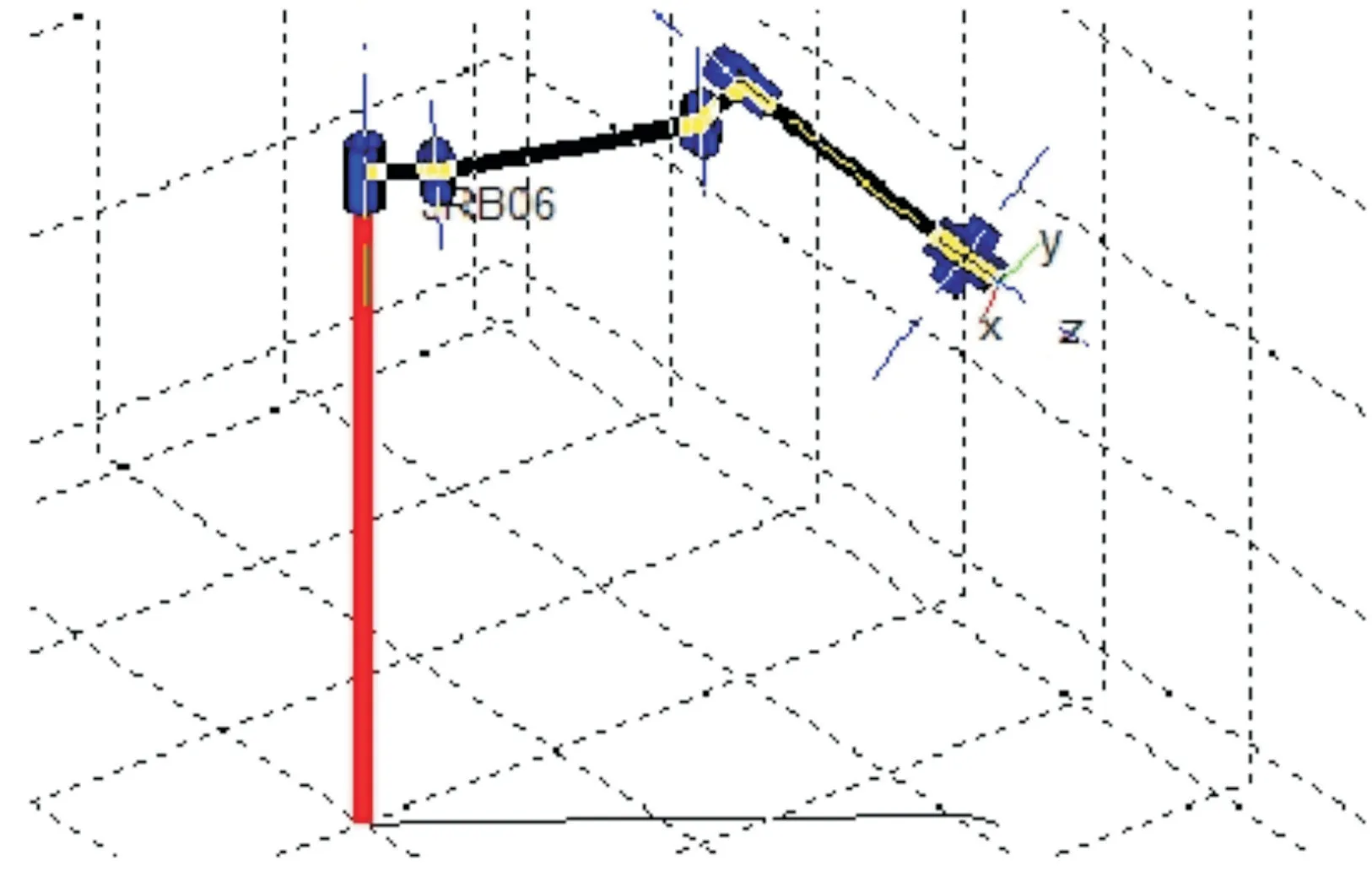
Fig.11 No.4,6 joints axis collinear singular simulation effect圖11 4、6 關(guān)節(jié)軸線共線奇異仿真效果
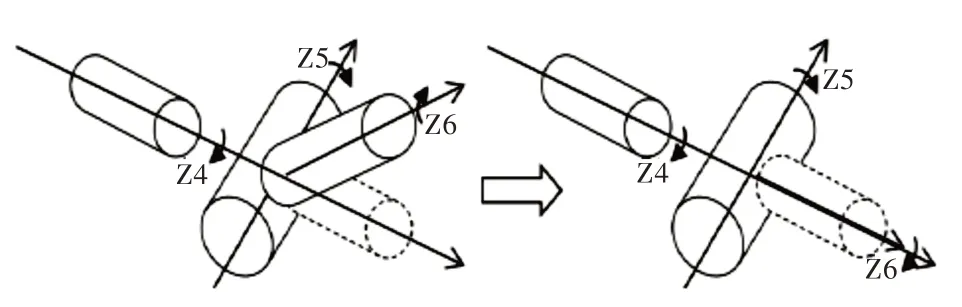
Fig.12 When the angle of No.5 joint is 0,the axis of No.4 and No.6 joints are collinear and strange圖12 5 號關(guān)節(jié)角為0 時,4、6 號關(guān)節(jié)軸線共線奇異
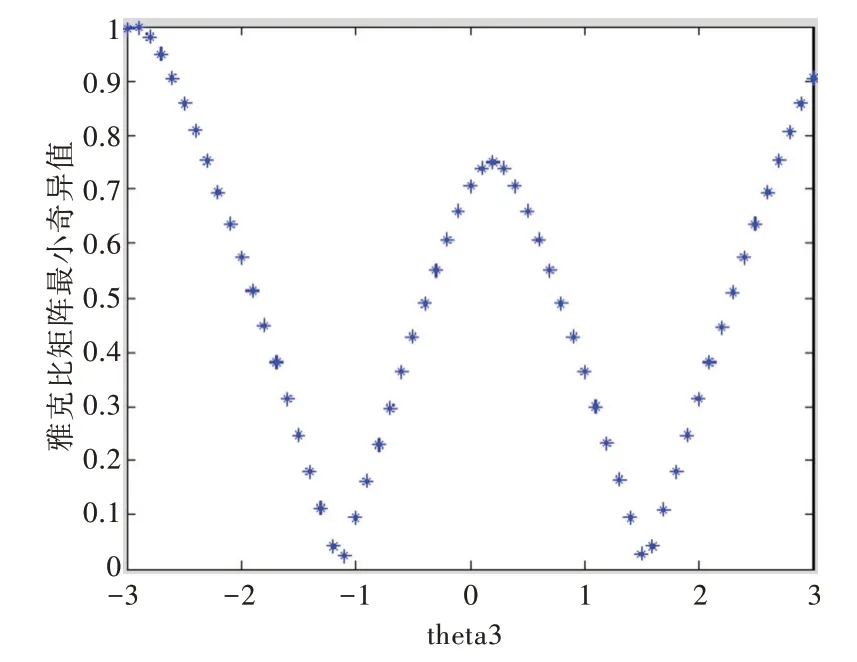
Fig.13 The relationship between the No.3 joint and the smallest singular value of the Jacobian matrix圖13 3 號關(guān)節(jié)與雅可比矩陣最小奇異值關(guān)系圖譜
Fig.14 Simulation effect of singularity of No.3 joint圖14 3 號關(guān)節(jié)奇異位形仿真效果

Fig.15 Simulation effect of singularity of No.3 joint and wrist圖15 3 號關(guān)節(jié)與腕部組合奇異位形仿真效果
此時過機械手臂腕部的3 個關(guān)節(jié)分別為4 號、5 號、6號,腕部交點與2、3 號關(guān)節(jié)軸線處于同一直線上,如圖16所示。
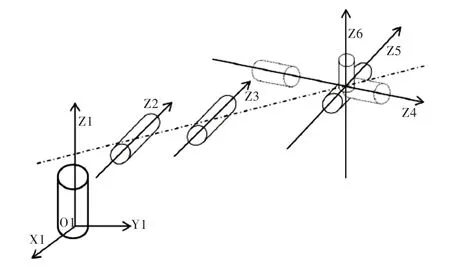
Fig.16 The intersection point of the wrist is on the same line as the axis of No.2 and No.3 joints圖16 腕部交點與2、3 號關(guān)節(jié)軸線處于同一直線上
(3)當(dāng)L1+L2C2+L3C(2+3) -L4S(2+3)=0 時,假如需要2 號關(guān)節(jié)與3 號關(guān)節(jié)滿足該關(guān)系式,將會使對應(yīng)雅克比矩陣行列式的值為0,從而導(dǎo)致機械手臂奇異位姿的產(chǎn)生。由于2 號關(guān)節(jié)與3 號關(guān)節(jié)兩者關(guān)節(jié)軸線互相平行,因此對旋轉(zhuǎn)機器人機械臂2 號關(guān)節(jié)、3 號關(guān)節(jié)角的限制條件簡化如下:

由上述關(guān)系式可知,2 號、3 號兩關(guān)節(jié)角度之間會形成一個奇異曲面,可運用MATLAB 對該曲面進行仿真。取滿足上式關(guān)系的2 號、3 號關(guān)節(jié)值36.26、168.5,關(guān)節(jié)2、關(guān)節(jié)3 產(chǎn)生的內(nèi)部奇異與腕部奇異組合仿真效果如圖17 所示,而與上述情形(2)的奇異組合仿真效果如圖18 所示。
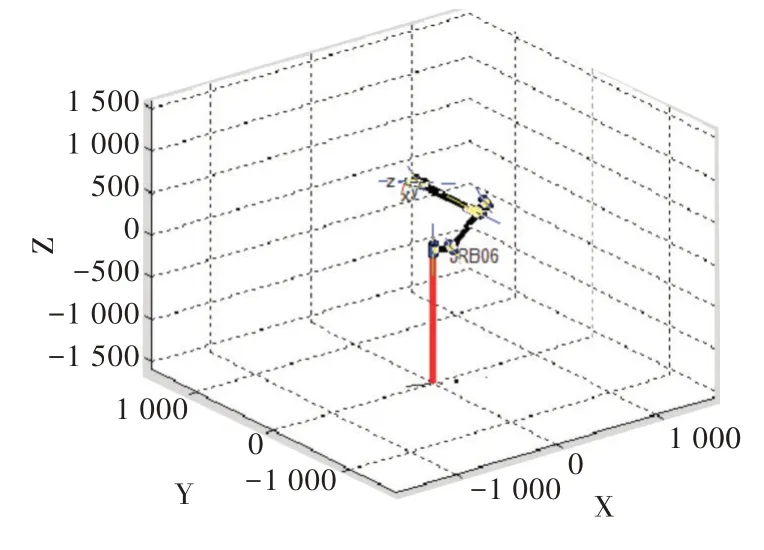
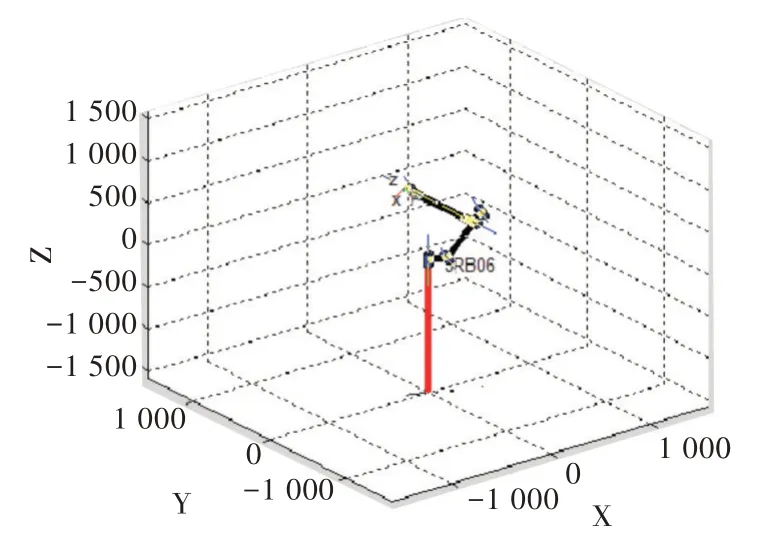
Fig.17 The combined simulation effect of internal singularity and wrist singularity produced by No.2 and No.3 joints圖17 關(guān)節(jié)2、關(guān)節(jié)3 產(chǎn)生的內(nèi)部奇異與腕部奇異組合仿真效果
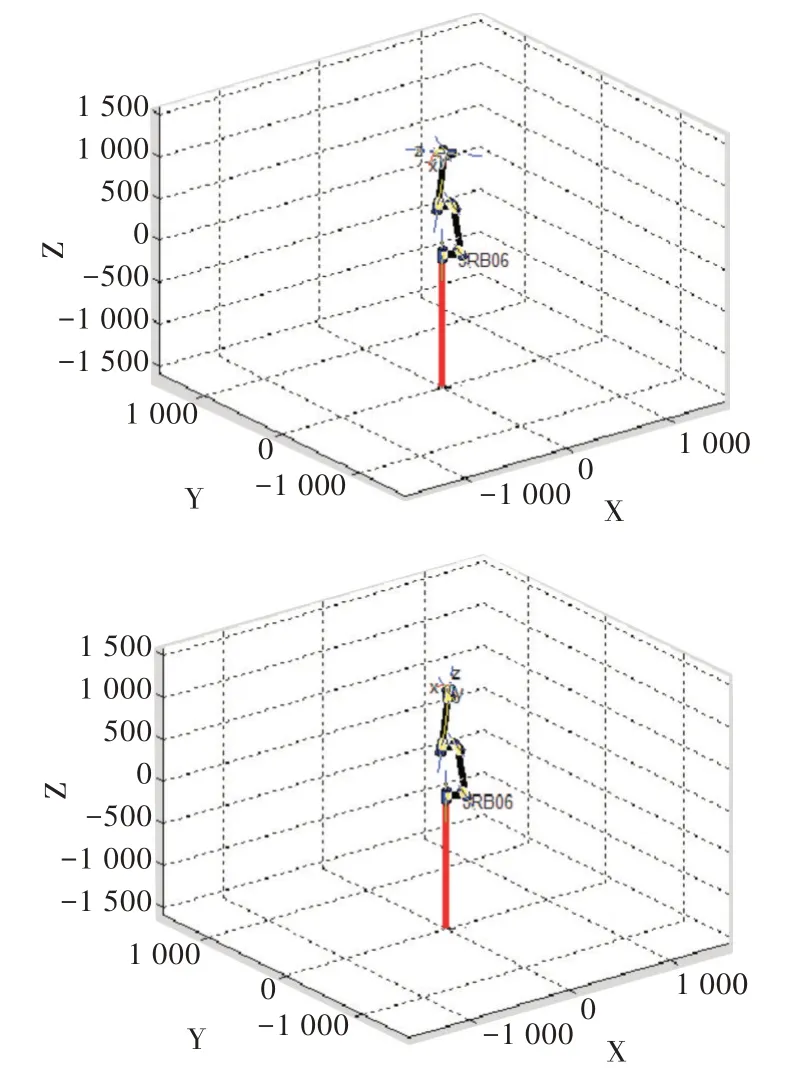
Fig.18 Simulation effect of singular combination between No.2 and No.3 joints wrist and situation (2)圖18 關(guān)節(jié)2、關(guān)節(jié)3、腕部與情形(2)之間奇異組合仿真效果
綜上可知,六關(guān)節(jié)旋轉(zhuǎn)機械手臂主要可能存在3 種奇異位形(即腕部的4 號與6 號關(guān)節(jié)共線、3 號關(guān)節(jié)出現(xiàn)某個極限邊界值、關(guān)節(jié)2 與關(guān)節(jié)3 在一定條件下發(fā)生內(nèi)部奇異的情況),以及這3 種奇異情形之間的組合情況。
4 結(jié)語
本文以某款旋轉(zhuǎn)機器人的串聯(lián)機械手臂作為研究對象,首先采用D-H 參數(shù)法搭建該機械手臂的運動學(xué)模型,進而求得其正運動方程,同時根據(jù)機械手臂各關(guān)節(jié)對應(yīng)參數(shù)值求解出該旋轉(zhuǎn)機器人手臂基坐標(biāo)系及機械手臂尾端位置信息;然后根據(jù)機械臂正運動方程構(gòu)造與之對應(yīng)的雅可比矩陣,進而求解出該機械手臂可能會發(fā)生奇異位形的所有情形;最后運用MATLAB 軟件的機器人工具箱,對求解出的奇異位形情況進行模擬仿真分析,從而驗證理論求解結(jié)果的正確性。
通過分析得到該旋轉(zhuǎn)機器人機械手臂所有可能發(fā)生奇異位形的情形,主要存在3 種奇異位形,以及3 種奇異情形之間的組合情況。本文研究可幫助該旋轉(zhuǎn)機器人機械手臂在執(zhí)行工作任務(wù)過程中規(guī)避特殊的運動形態(tài)以避免出現(xiàn)奇異位姿,提供十分重要的理論分析數(shù)據(jù),對機械臂后續(xù)研發(fā)工作具有一定的實際意義。

