考慮氣壓的晴空大氣下行長波輻射參數化方案及其適用性分析*

孟 琦

1 中國科學院青藏高原研究所，北京 100085 2 中國科學院大學，北京 100049

提 要： 基于Prata晴空大氣下行長波輻射參數化方案，針對其在高原地區及可降水量較小地區理論精度較差的缺點，考慮不同高度的大氣柱發射的長波輻射量不同，提出了三種考慮氣壓的大氣下行長波輻射參數化方案，通過全球ERA-5再分析數據進行最小二乘擬合確定經驗常數并在全球不同區域對其適用性進行了分析。模擬結果表明，考慮氣壓的參數化方案有效地改善了可降水量減小時Prata方案大氣發射率收斂過快的不足，三種新方案在青藏高原安多地區和南美洲圣路易斯地區的下行長波輻射模擬結果相對于觀測值和ERA-5再分析數據的平均偏差和均方根誤差均更小，模擬精度相對Prata方案均有提高，適用性更強。

引 言

大氣發射的下行長波輻射是全球輻射能量收支平衡中一個非常重要的成分，也是地表輻射模型中輻射預算的關鍵組成部分，準確計算大氣下行長波輻射有利于了解影響地表能量平衡的因素(Zhu et al,2017)。同時,大氣下行長波輻射研究在預報夜間霜凍、霧、溫度變化、云量及改善區域天氣預報、確定輻射冷卻率、衡量氣候變化和計算全球增暖等方面也發揮著重要作用(彭麗春等，2015)。

目前獲得晴空下行長波輻射的方法主要有三種：地面氣象站輻射計直接觀測、根據復雜的大氣輻射傳輸模型精確計算及通過經驗公式計算獲得。輻射計直接觀測能方便準確地得到下行長波輻射值，但地面觀測站點分布不均，因此大部分地區不具備直接觀測的條件，目前只有部分國家氣象觀測站能獲取相關數據(李偉斌等，2015)。在已知整層大氣的垂直分布特性的條件下利用探空數據，通過復雜的大氣輻射傳輸模型，可以獲得下行長波輻射的理論值，然而由于探空數據不易獲取，使用上述輻射傳輸模型計算時，常受到輸入數據缺乏的限制(周允華，1984)。通過經驗公式進行計算具有模型簡單、觀測數據(近地面氣溫、氣壓、水汽壓等)易獲得的優勢，因此具有很強的實用性，在許多領域得到了廣泛的應用(余珊珊等，2011；Alados et al,2012)。例如Zhu et al(2017)在青藏高原地區對Brutsaert(1975)、Garratt(1992)、Prata(1996)和Swinbank(1963)等13個參數化方案進行了局地校正，獲得了適用于該地區的參數化方案。近年來，下行長波輻射參數化研究取得了豐碩成果，例如Prata(1996)提出的參數化方案有效地改善了極端氣候條件下的模擬精度，物理意義更加嚴謹，且適用性更強。Yu et al(2013)利用衛星熱紅外數據提出了具有高分辨率優勢的參數化方案，后來又基于MODIS數據對該方案進行了改進，將模擬精度和適用性進一步提高(Yu et al, 2019)。Zhou et al(2019)利用中分辨率成像光譜儀數據及地面實測資料，基于多元自適應回歸方法進行了晴空大氣下行長波輻射計算，并在全球范圍7個站點進行了驗證。隨著遙感科學的發展，氣象觀測的時空分辨率不斷提高，下行長波輻射參數化方案模擬精度和適用性也得到了改善，但目前基于大氣參數的參數化方案通常不具備廣泛的適用性，尤其是在高海拔或干旱地區，通常存在較大的偏差，且誤差會隨著海拔的升高而增大，制約了參數化方案的適用性(Gubler et al,2012)。

我國幅員遼闊，地形與氣候條件較為復雜，利用上述參數化方案對晴空下行長波輻射進行理論計算的精確度難以滿足要求。以青藏高原為例，由于其地處高寒地區，地面有效輻射和輻射平衡具有大致相同的量值，因此，下行長波輻射的精確估計對于高原地面輻射平衡和加熱場的研究具有重要意義(周允華，1984；黃妙芬等，2005)。其次，入射長波輻射是青藏高原地區冰川融化的能量來源，利用準確的下行長波輻射值，有助于獲得準確的模擬蒸散和冰川排放的結果，這對于冰川災害預防、綠洲農業用水甚至西藏地區社會經濟的整體發展都是必不可少的(Zhu et al,2017；Ohmura,2001；Sedlar and Hock，2009)。此外，研究高寒地區晴空下行長波輻射對光能的利用具有指導性意義，可為新的清潔能源的開發提供積極廣闊的前景。同時青藏高原對我國的氣候變化有著重要的影響，精確地定量研究該地區的晴空下行長波輻射，對研究我國天氣氣候變化也有著重要意義。然而晴空下行長波輻射數據的缺乏，是能量平衡、氣候模擬等研究常常面臨的困難(余珊珊等，2011；閔敏和吳曉，2019)。

針對目前晴空大氣下行長波輻射參數化方案在青藏高原及其他干旱地區適用性較差的問題，本研究基于Prata的參數化方案，考慮到入射到地面的長波輻射來自整層大氣，對于不同海拔的地區來說，大氣柱的高度不同，下行長波輻射值也不同，由此引進氣壓因素，根據ERA-5的再分析數據，通過多元函數擬合，獲得了新形式的晴空大氣發射率參數化方案，進而根據站點資料在全球不同海拔地區進行了模擬，與站點資料的下行長波輻射的觀測值進行了對比，分析了新參數化方案在青藏高原及其他地區的適用性。

1 物理背景

入射到地面的大氣下行長波輻射是其上整層大氣發射的，與大氣層溫度和濕度的垂直分布、厚度密切相關，理論上可表示為垂直分層大氣的積分形式。Steffan-Boltzman公式是近似計算長波輻射的常用公式，但該公式只適用于黑體，對于非黑體的大氣來說，則需要考慮大氣發射率。根據該公式，在晴空條件下，大氣下行長波輻射計算公式可近似表示為：

(1)

式中:LWd為晴空大氣下行長波輻射，單位為W·m-2；εa為晴空大氣發射率；Ta通常取近地面大氣溫度代替整層大氣的發射等效溫度，單位為K；σ為玻爾茲曼常數，其值為5.67×10-8W·m-2·K-4。

由于晴空大氣發射率無法通過直接測量獲得，Brunt(1932)基于熱傳導與輻射傳遞之間的相似性，提出了晴空大氣發射率與近地面水汽壓相關的經驗公式(Crawford and Duchon,1999)：

(2)

式中：e為近地面水汽壓，單位為hPa；a、b為經驗常數，a值約在0.34～0.66，b值約在0.033～0.127。由于經驗常數因地區而異，給應用帶來了不便。Swinbank(1963)指出下行長波輻射與水汽壓之間并無關系，而僅僅與溫度的平方有關，且Brunt(1932)經驗公式有效的原因是水汽壓與溫度的正相關關系，進而提出了僅與近地面氣溫相關的經驗公式(盛裴軒等，2013)：

(3)

式中：常數a=5.31×10-14/σ;Ta為近地面氣溫，單位為K。

由于上式的常數不隨地點而變，觀測到的和估計的晴空大氣下行長波輻射之間的相關系數為0.99，因而被廣泛采用，但在高海拔地區，因水汽吸收的壓力效應，需做高度校正(盛裴軒等，2013)。Brutsaert(1975)基于Schwarzschild方程和標準大氣假設，提出了物理意義更嚴格的參數化方案：

(4)

從式中可以看出當水汽壓為0時，該參數化方案得到的晴空大氣發射率為0，但實際上，即使水汽含量為0，具有一定溫度的大氣同樣能發射長波輻射，因此晴空大氣發射率不應為0，故此結果并不能完全適用于計算晴空大氣發射率。Prata(1996)指出，基于對單個氣體吸收帶的窄帶模型和寬帶模型的了解，可以用修正的指數帶模型近似表示整個長波頻譜，同時應考慮對水汽路徑不均勻性加以修正，據此將輻射傳輸過程進行了高度簡化近似，考慮了溫度、濕度的垂直影響，引入了大氣可降水量，提出了以下形式的參數化方案：

εa=1-(1+w)e[-(a1+a2w)m]

(5)

式中：a1，a2和m是經驗常數，a1和a2通過最小二乘擬合的方法獲得，分別取1.2和3.0，m取1/2。w是大氣可降水量，單位為g·cm-2，可以根據以下方式進行計算：

(6)

式中：c是一個常數，標準大氣壓假設下其取值為46.5。該參數化方案具有以下良好特性：當大氣可降水量趨近于0，即大氣接近為干空氣時，只要具有一定溫度，大氣依然發出下行長波輻射，此時晴空大氣發射率是一個常數，且該參數化方案估算的晴空大氣發射率不會超過黑體的發射率。需要說明，隨著海拔高度的升高，此參數化方案結果與觀測值的均方根誤差會增大，例如在海拔為3 580 m時，均方根誤差達到長波輻射值的15%(Prata，1996)。鑒于此，本研究認為大氣柱的厚度會對大氣發射率產生影響，而長波輻射參數化方案在高寒地區的應用有望結合氣壓加以改進。

2 引入氣壓的參數化方案

由于Prata參數化方案具有干空氣條件下，下行長波輻射依然存在和晴空大氣發射率不超過黑體發射率的優點，本研究在Prata參數化方案的基礎上，引入了氣壓因素，提出了以下三種形式的晴空大氣發射率的參數化計算方案：

ε≈1-(1+w)(1+ζ)e-(aw+bζ)c

(7)

ε≈1-(1+w)(1+ζ)e-[awb+cζd+f(wζ)g]c

(8)

ε≈1-e-[awb+cζd+f(wζ)g]c

(9)

式中：ζ=(p/p0)，p為當地大氣壓，p0為標準大氣壓，w是大氣可降水量，a、b、c、d、f、g均為經驗常數。這里分別稱式(7)～式(9)為方案1、方案2和方案3，上述三種方案中當氣壓趨近于0時，大氣可降水量w趨近于0，則此時晴空大氣發射率也趨近于0，且引入氣壓項后，晴空大氣發射率依然不會超過黑體發射率。三種方案均保留了Prata方案在極限條件下的優良特性，但表達形式不同，大氣發射率模擬結果也不相同。方案1參照了Prata進行水汽改正時的方法，在指數部分和系數部分同時添加氣壓項，方案2和方案3在方案1的基礎上考慮了可降水量與氣壓的交互影響，因此理論上極限情況下表現更好。以上三種參數化方案中的經驗常數通過使用2018年每月1日ERA-5全球再分析數據進行最小二乘擬合的方法獲得。再分析數據包含全球范圍的近地面氣溫、露點溫度、氣壓、大氣可降水量以及晴空大氣下行長波輻射值，時間分辨率為1 h，空間分辨率為0.25°。為了充分考慮不同氣壓條件下長波輻射的差異，本研究對擬合數據進行了篩選，將每小時全球各點的氣壓值均從小到大排序并形成十個區間，在每個氣壓區間中隨機挑選100個氣壓值，對應100個地面點，擬合樣本容量為288 000個。作為示例，圖1給出了經篩選后2018年1月1日00時全球范圍內用于擬合的數據對應的地面點分布，紅色的點表示此時經過篩選的站點。

從圖1中可以看出，青藏高原地區等高海拔地區數據覆蓋程度較高，因此晴空數據篩選結果能夠更好地保證高海拔地區擬合結果的準確性，這也正是對再分析數據進行篩選的目的。在此基礎上經過最小二乘擬合處理后，得到三種考慮氣壓影響的晴空下行長波輻射參數化方案的經驗系數見表1。

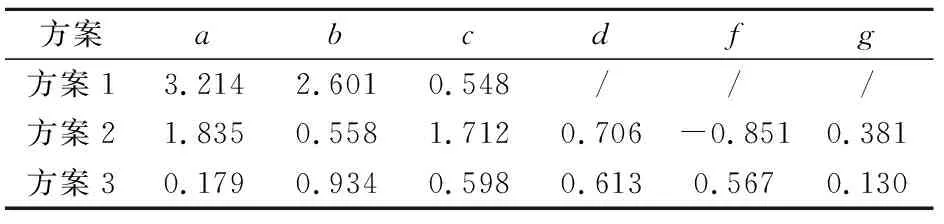
表1 考慮氣壓的參數化方案經驗系數擬合結果Table 1 Empirical coefficients of parameterized schemes considering air pressure

為了研究上述三種參數化方案對晴空大氣發射率的模擬效果，本文將對應時間ERA-5再分析數據中獲得的所有站點的晴空大氣發射率作為參照(即實際值)，分別求得三種參數化方案模擬結果的平均偏差、均方根誤差及與參照大氣發射率的相關系數并做散點密度圖，同時將Prata模型的模擬結果作為對照，比較不同的參數化方案的模擬精度。

圖2a～2d分別給出了本研究提出的三種新參數化方案及Prata參數化方案在全球按海拔均勻分布的多個隨機站點(包含平原地區和高原地區)的晴空大氣發射率散點密度，模擬時間為2018年每月1日，時間分辨率為1 h，樣本容量為288 000。圖中橫軸為根據ERA-5再分析數據中晴空下行長波輻射得到的晴空大氣發射率，根據式(1)有：

(10)

縱軸為考慮氣壓的參數化方案與Prata參數化方案，分別通過ERA-5氣壓與可降水量數據計算得到的晴空大氣發射率理論值，顏色表示散點密度，顏色越亮則該區域散點密度越大。從圖中可以看出，考慮氣壓影響的三種參數化方案得到的晴空大氣發射率理論值與實際值基本上表現出斜率為1的線性關系，而對于Prata參數化方案而言，由于其在大氣可降水量不斷減小時大氣發射率逐漸收斂于0.665左右，因此對于大氣發射率小于該極限值的情況無法進行模擬，這也解釋了該參數化方案應用于大氣可降水量較小的地區時而造成精度較低的問題。三種考慮氣壓的參數化方案與Prata參數化方案晴空大氣發射率模擬結果相較于ERA-5數據的平均偏差(MBE)、均方根誤差(RMSE)及相關系數(R)計算結果見表2。

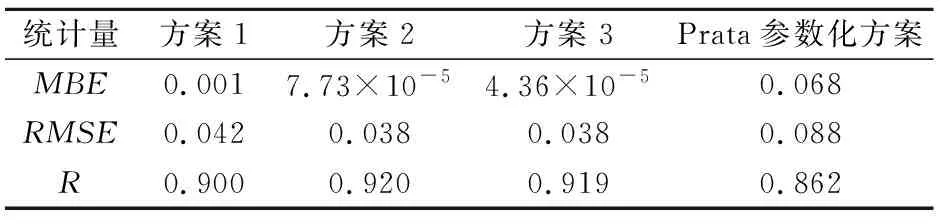
表2 新參數化方案與Prata參數化方案晴空大氣發射率相對于ERA-5數據的MBE、RMSE和RTable 2 Mean bias error, root mean square error and correlation coefficient of new parameterizations and Prata parameterization corresponding to ERA-5 reanalysis data

從表2中可以看到，相對于ERA-5再分析數據，方案2和方案3的MBE較小，其中方案3的MBE僅為4.36×10-5，Prata參數化方案的MBE較大，為0.068；對于RMSE和R而言，方案1、方案2及方案3亦均顯著優于Prata參數化方案，其中方案2和方案3精度更高，相關性更好。因此，本研究所提出的三種參數化方案相比Prata的參數化方案能更精確地對晴空大氣發射率進行模擬，尤其是在高海拔大氣可降水量較小的區域，理論上能夠彌補Prata參數化方案過早收斂的缺陷。

3 適用性分析

上一節中晴空大氣發射率參數化方案的擬合數據是經過篩選的全球數據，因此理論上三種新的參數化方案可對全球范圍具有不同氣壓和可降水量條件地區的晴空下行長波輻射進行模擬。為了進一步分析三種新的參數化方案在青藏高原及其他地區的適用性，本研究對青藏高原及其他地區的晴空下行長波輻射進行了理論計算，以位于青藏高原的安多縣(海拔5 200 m)和位于阿根廷圣路易斯(海拔500 m)的兩個站點為例，本文給出了利用站點數據對新方案與Prata方案的模擬效果進行比較的結果。

對安多地區晴空下行長波輻射的模擬使用了該地區1998年5月11日至9月16日的站點數據，包括氣壓、近地面氣溫、相對濕度等觀測值。本研究通過計算云量的方法獲取晴空時間(Zhu et al,2017)：

(11)

式中：n表示云量，Sin表示實測太陽下行短波輻射值，Sclear為晴空時太陽下行短波輻射值，二者單位均為W·m-2，后者可以通過理論模型計算獲得。由于夜間太陽下行短波輻射減弱為0 W·m-2，因此上述方法無法獲取夜晚晴空時間，本研究僅取太陽天頂角小于70°且n值小于0.05時作為晴空。用于計算的大氣可降水量無法通過觀測獲得，目前常用的推算大氣可降水量的方法包括探空資料計算、地面氣象資料推算、地基GPS探測資料反演等。由于目前探空資料和GPS數據較為缺乏，本研究中采用站點資料，根據經驗公式計算青藏高原地區大氣可降水量(Yang et al,2010)：

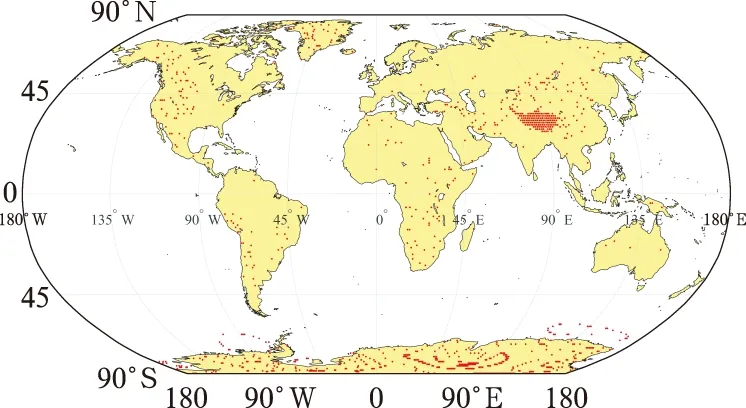
圖1 2018年1月1日00時擬合數據對應的地面點分布Fig.1 Ground points corresponding to the data used for fitting at 00:00 BT 1 January 2018

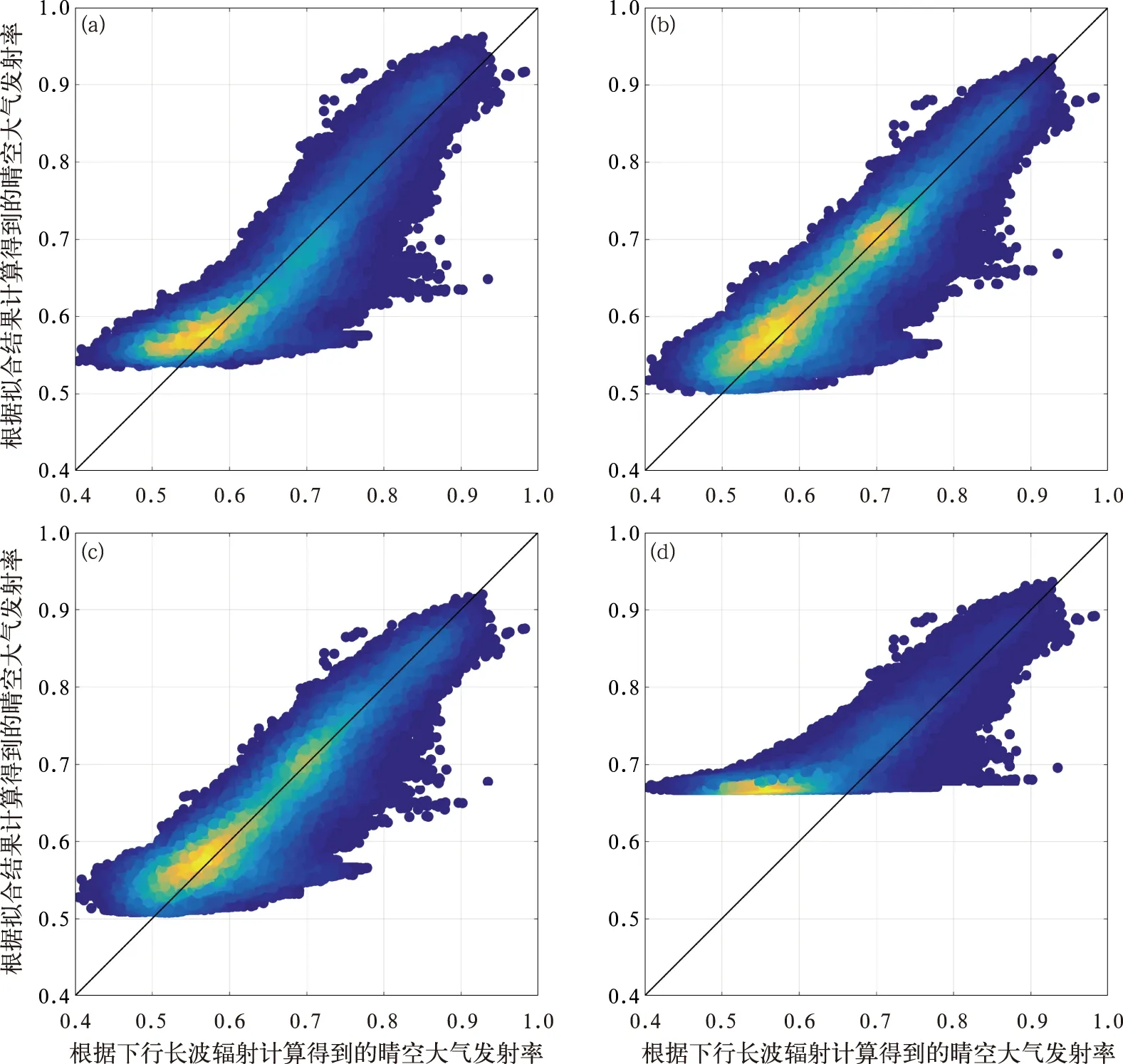
圖2 方案1(a)，方案2(b)，方案3(c)和Prata方案(d)晴空大氣發射率模擬結果散點密度Fig.2 Simulation results of clear sky atmospheric emissivity of Scheme 1 (a), Scheme 2 (b), Scheme 3 (c) and Prata’s Scheme (d)

(12)

式中:RHa為站點的相對濕度;w為大氣可降水量，單位為g·cm-2；Ta為氣溫，單位為K。得到晴空時間與可降水量后即可計算各參數化方案的晴空大氣下行長波輻射理論值，并與下行長波輻射觀測數據進行對比分析其誤差。

圖3a～3d分別給出了根據方案1、方案2、方案3及Prata方案使用安多站點數據對該地區的晴空大氣下行長波輻射的模擬結果。從圖中可以看出，Prata參數化方案在青藏高原地區下行長波輻射較小時模擬效果較差，理論值普遍偏大，這與前面提到的該方案在晴空發射率較小時精度降低相一致。引入氣壓的三種新方案模擬的結果與下行長波輻射觀測值更加吻合。表3給出了該站點上述四種方案的MBE、RMSE及R。

從表3中可以看出，三種考慮氣壓的參數化方案模擬結果的MBE、RMSE相對Prata方案均較小，說明引入氣壓后的參數化方案有效地改善了Prata參數化方案在青藏高原地區的模擬精度，在青藏高原的適用性更強。

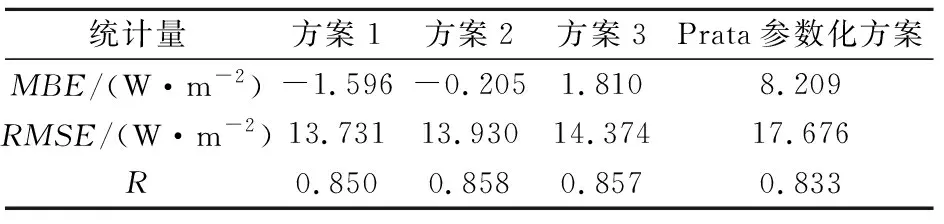
表3 安多地區新參數化方案與Prata參數化方案晴空大氣下行長波輻射相對于觀測數據的MBE、RMSE和RTable 3 Mean bias error, root mean square error and correlation coefficient of new parameterizations and Prata parameterization corresponding to observed data in Amdo

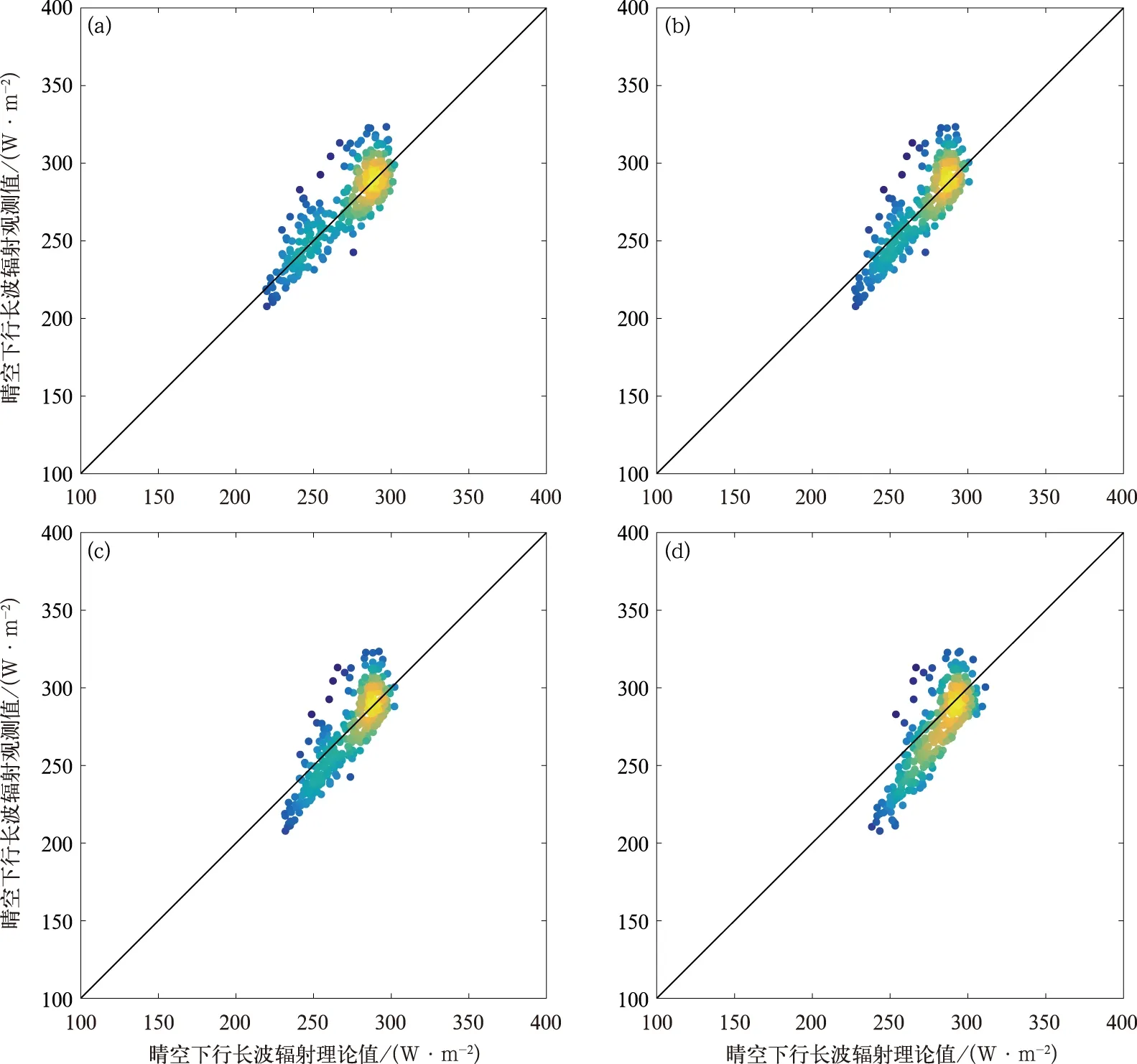
圖3 安多站點方案1(a)，方案2(b)，方案3(c)及Prata方案(d)晴空向下長波輻射模擬結果散點密度Fig.3 Simulation results of longwave radiation in clear sky of Scheme 1 (a), Scheme 2 (b), Scheme 3 (c) and Prata’s (d) in Amdo

由于圣路易斯與安多地區氣象條件差異較大，本研究在對圣路易斯地區應用經驗公式(16)計算理論大氣可降水量時將理論可降水量與ERA-5再分析數據可降水量進行了比較，發現理論值較再分析數據普遍偏小，其RMSE達到6.6 g·cm-2，因此該經驗公式無法準確估計圣路易斯地區大氣可降水量情況。為了驗證引入氣壓的參數化方案在該地區的適用性，大氣可降水量采用2014年ERA-5再分析數據，晴空時間的獲取方法與安多地區相同。

圖4a～4d分別給出了根據方案1、方案2、方案3及Prata方案使用站點數據對圣路易斯地區的晴空大氣下行長波輻射的模擬結果。從圖4d中可以看出，Prata參數化方案的晴空下行長波輻射模擬結果相比于ERA-5再分析數據普遍偏大，而引入氣壓的新參數化方案理論值與再分析數據的吻合情況更好。表4給出了圣路易斯地區上述四種方案的MBE、RMSE及R。

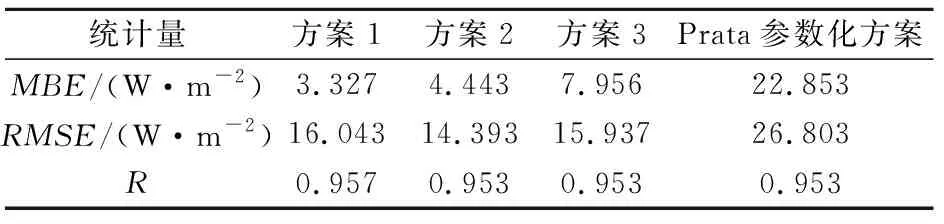
表4 同表3，但為圣路易斯地區Table 4 Same as Table 3, but in San Luis

根據表4可知，考慮氣壓的新方案的MBE、RMSE均明顯小于Prata參數化方案，三種新方案的模擬精度相當，方案2的RMSE最小，為14.393 W·m-2，方案1和方案3的RMSE相對較大，分別為16.043和15.937 W·m-2，因此在圣路易斯地區方案2的模擬精度相對更高，而考慮氣壓的參數化方案相較于Prata方案適用性更強。需要指出的是，本研究中參數化方案的適用性分析沒有考慮局地校正，而是將最小二乘擬合結果直接應用于不同氣壓條件的站點，分析引入氣壓后的方案相對于不考慮氣壓的方案的改善情況，而結合對安多地區和圣路易斯地區模擬結果的分析可知，新參數化方案對不同地區晴空大氣下行長波輻射理論計算的精度均有較為明顯的改善。

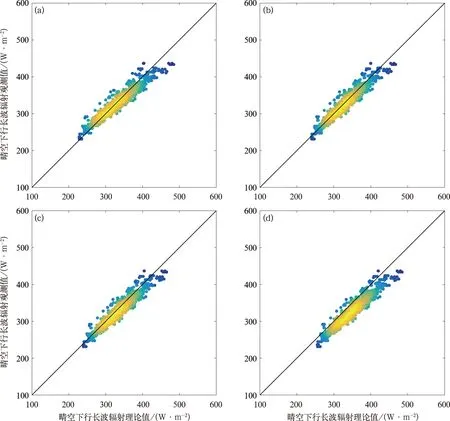
圖4 同圖3，但為圣路易斯站點Fig.4 Same as Fig.3, but in San Luis

4 結論與討論

本研究基于Prata提出的晴空大氣下行長波輻射參數化方案，針對其對高原地區下行長波輻射模擬結果誤差較大及可降水量較小時大氣發射率過早收斂的問題，考慮到不同長度的大氣柱下行長波輻射發射量不同，通過引入氣壓作為新變量提出了三種新的晴空下行長波輻射參數化方案。新方案保留了Prata參數化方案的優點，當大氣可降水量趨近于0時，大氣依然發出下行長波輻射，此時晴空大氣發射率收斂為一個常數，且該參數化方案估算的晴空大氣發射率不會超過黑體的發射率。新方案的經驗參數由全球ERA-5再分析數據通過最小二乘擬合的方式獲得，在擬合的過程中充分考慮了高原地區大氣壓偏小的特點。本研究在不同地區使用新的參數化方案對晴空大氣下行長波輻射進行了模擬，通過模擬精度的比較分析其在不同氣象條件下的適用性。青藏高原的安多地區下行長波輻射模擬結果表明，引入氣壓的三種新的參數化方案能有效地改善Prata參數化方案在水汽較少時模擬精度明顯降低的缺點，相對于下行長波輻射觀測結果，三種新方案模擬結果的MBE分別為-1.596、 -0.205和1.810 W·m-2，RMSE分別為13.731、13.930和14.374 W·m-2，較Prata方案均更小，表明在青藏高原等高海拔地區新方案的適用性優于Prata方案。對南美洲圣路易斯地區的晴空下行長波輻射模擬結果表明，Prata參數化方案的模擬結果相對于ERA-5再分析長波輻射數據整體偏大，其MBE、RMSE分別為22.853和26.803 W·m-2，而新方案的模擬結果與再分析數據更加吻合，MBE分別僅為3.327、4.443和7.956 W·m-2，RMSE也有明顯的改善，分別為16.043、14.393和15.937 W·m-2，因此在低海拔地區，引入氣壓的新參數化方案的適用性同樣優于Prata參數化方案。

為了便于研究引入氣壓后的參數化方案相比于Prata方案模擬精度上的提高，分析不同方案的適用性，本文中的Prata參數化方案與考慮氣壓的新方案在適用性分析的過程中均沒有經過局地校正，而事實上，下行長波輻射參數化方案經過局地校正后能有效地提高模擬精度。局地校正指的是確定參數化方案后，以特定的站點或區域數據為依據對方案進行擬合確定經驗常數的方法，通過局地校正通常可以獲得適用于該地區或該站點且精度較高的理論模型，例如Zhu et al(2017)研究指出，經過局地校正的青藏高原慕士塔格峰、扎當冰川等地的下行長波輻射參數化模型相較于未進行局地校正的模型，其MBE由-6 W·m-2減小為0.1 W·m-2，RMSE由14 W·m-2減小為9.6 W·m-2(Zhu et al,2017)，因此本研究的三種考慮氣壓的參數化方案有望在局地校正后獲得更高的精度，這會在將來的研究中加以驗證。此外，由于大氣可降水量無法直接觀測，利用站點數據對下行長波輻射進行理論精確模擬需要具備適用于該站點的大氣可降水量模型，根據本文對可降水量理論計算的結果可知，現有的可降水量模型無法適用于不同氣象條件的站點，因此發展能精確計算站點大氣可降水量的理論模型，也需要在將來的研究中進一步考慮。