運用SAS廣義線性混合模型分析裂區試驗數據

張久權, 李彩斌, 凌愛芬, 董建新

(1.中國農業科學院煙草研究所, 農業農村部煙草生物學與加工重點實驗室, 山東 青島 266101; 2.貴州省煙草公司畢節市公司, 貴州 畢節 551700; 3.四川省煙草公司涼山州公司, 四川 西昌 615000)

裂區設計由于能夠突破試驗條件限制，為實際操作提供方便等諸多優點[1]，受到廣大科研人員的普遍歡迎，在許多研究領域得到廣泛運用[2-11]。然而，由于此類試驗數據的統計分析較難，F檢驗的主區因子和副區因子所用的誤差項不同[4,6]，主區因子間、同一主區因子不同副區因子間均值比較的t值計算方法也不同[1,12]，使裂區試驗的數據分析具有很大挑戰性。如果僅依賴計算機軟件程序進行統計分析，一般很難處理，有些需要手工計算，但計算量很大[1]。從國內外研究進展看，人們對裂區設計的統計分析常常存在誤用的現象[2,13]。Yossa等[14]調查表明，65%的已發表SCI論文存在試驗設計、F檢驗或多重比較錯誤。其中，裂區設計占比較大，但目前有關裂區設計試驗的統計方法存在不系統或太復雜等問題，通常需要手工計算，給科技工作者增加了負擔。

傳統上，學者們在利用SAS程序進行裂區設計的方差分析和均值比較時，主要采用一般線性模型(general linear model，GLM)程序模塊，而該程序模塊是在20世紀80年代開發的，當時沒有考慮到在進行裂區設計的F檢驗時，主區因子與副區因子需采用不同的誤差均方與自由度，均值比較也需采用不同的誤差均方和自由度，因而計算F值時需要編寫大量的復雜代碼來進行修正[15]。后來，雖然可以用 “h=……”語句進行彌補，但是進行處理間均值比較時，需要選用合適的、不同的誤差項。然而，對于某些情況，GLM程序模塊沒有可用于定義所需誤差項的選項，所以誤差項無法列出[15]。

近年來，SAS等商業軟件進行了創新，廣義線性混合模型(general linear mixed model，GLIMMIX)有了很大發展[15]，其能適用于多種分布的變量[16]。本研究應用SAS的GLIMMIX程序模塊對裂區試驗數據進行方差分析和均值比較，通過與傳統的GLM程序模塊和混合模型(MIXED)程序模塊進行對比，介紹GLIMMIX 程序模塊在裂區試驗數據統計中的優勢，以供廣大科技工作者參考。

1 材料與方法

1.1 試驗材料與設計

裂區試驗的處理設計一般采用全因子試驗，即各因子的水平全部交叉，構成完整的處理組合。關于主、副區因子的確定與分配，參照張久權等[1]方法。下面將采用其中實例進行試驗設計和原始數據分析，實例設計如下。

第一年在福建省三明市進行烤煙品種比較試驗，單因子4水平隨機區組設計，4水平為4個烤煙品種(翠碧1號、KRK26、YN116、CF209)，重復3次。第二年，為了探明移栽期對各品種產量的影響，對4個品種增加了3個移栽期:1月24日(1)、1月31日(2)、2月8日(3)處理，試驗改為裂區設計，品種為主區因子，移栽期為副區因子。第二年的產量數據見表1。

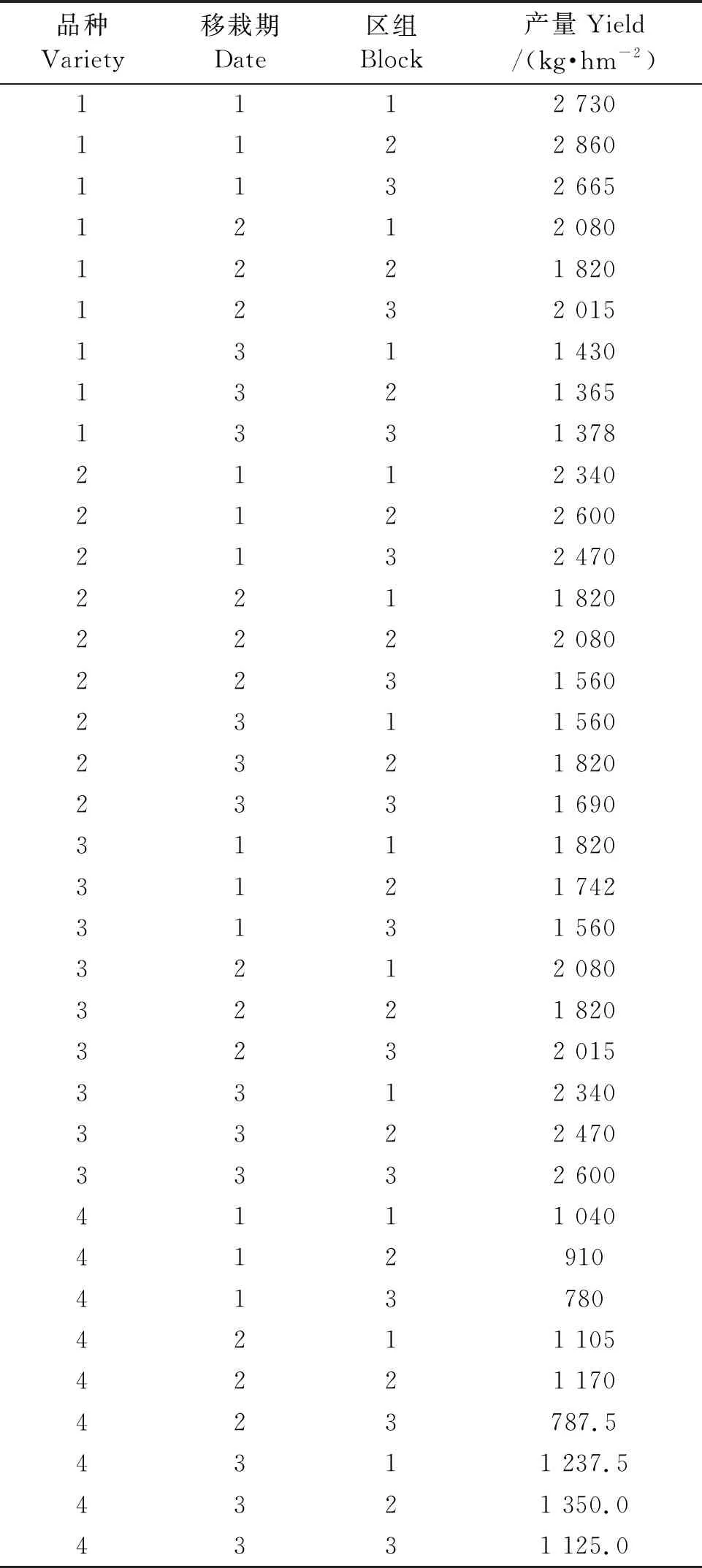
表1 產量數據Excel輸入表Table 1 Yield data entry for Excel

1.2 方差分析模型

對于兩因素裂區設計，如果主區因子的排列為隨機區組，副區因子在主區內隨機排列，其線性可加效應模型如下。

Yijk=μ+αi+βj+αiβj+rk+wik+eijk

(1)

式中，Yijk為某小區的觀察值，如小區產量；μ為總體均數；αi為主區因素A第i水平的效應，βj為副區因素B第j水平的效應，αiβj為A因素i水平與B因素j水平交互作用效應，均為固定效應；rk為區組K的效應，wik為主區誤差，eijk為副區誤差，均為隨機效應。為了便于理解，將主區元素放在前，副區元素放在后，將(1)式改寫為(2)式。

Yijk=μ+rk+αi+wik+βj+αiβj+eijk

(2)

式中，區組效應rk，主區誤差wik和副區誤差eijk應滿足以下條件。

(1)所有的隨機效應項rk、wik和eijk相互獨立。

(2)區組效應rk為iidN(0, σR2)，即rk服從同一正態分布，相互獨立，方差均為σR2。

(3)主區誤差wik為iidN(0, σw2)。

(4)副區誤差eijk為iidN(0, σ2)。

從模型可看出，對于這類資料的分析可以分兩步。第一步，將總變異分解為主區組間變異、主區因子間變異和主區誤差；第二步，將整個試驗的總變異分解為主區變異、副區因子變異、主副因子之間的交互作用和副區誤差。

如果主區因子為完全隨機，需要將公式(1)和(2)中的區組效應rk刪除。其他試驗設計的線性模型依此類推。

1.3 方差分析和多重比較SAS程序

1.3.1用GLIMMIX模塊進行F檢驗和所有處理組合間的均值比較 運用SAS 9.4軟件的GLIMMIX模塊對表1數據進行F檢驗。SAS程序1的代碼如下。

ODS RTF;

ODS graphics on;

PROC IMPORT

OUT= split

DATAFILE= "E:yancao.xls"

DBMS=EXCEL REPLACE;

SHEET="Sheet1$";

GETNAMES=YES;

RUN;

PROC GLIMMIX data = split;

Class block variety date;

Model yield = variety date variety*date / ddfm=satterth;

Random block block*variety;

Lsmeans variety*date/plot=meanplot (sliceby=variety join);

Lsmeans variety date variety*date /diff;

Lsmestimate variety*date ′date1 vs date2 in variety1 ′ 1 -10;

RUN;

ODS graphics off;

ODS RTF close;

程序說明：輸入代碼時注意分號為英文字符。數據文件存放地址為E:yancao.xls sheet1，數據格式見表1。PROC IMPORT直接讀取EXCEL文件的數據。其他數據格式如文本格式也可以輸入，但EXCEL比較方便。PROC GLIMMIX調用GLIMMIX程序，采用限定的最大似然法進行F檢驗和多重比較。Class 語句列出所有的分類變量。Model語句“=”右邊只需列出固定效應變量。ddfm=satterth對誤差方差、自由度等進行校正，以保證F值的正確性。“Lsmeans variety*date/plot = meanplot (sliceby=variety join)”語句輸出交互作用效果圖，join選項將各點連成曲線。“Lsmeans variety*date /diff” 語句對所有處理水平組合的最小二乘均值(least square means，lsmean)進行兩兩比較，計算t值和差異顯著性。在平衡的試驗設計中，最小二乘均值與處理均值相同。

1.3.2用GLIMMIX模塊進行F檢驗和部分處理組合間的均值比較 SAS程序1中的語句“Lsmeans variety date variety*date /diff;”輸出所有處理組合的最小二乘均值及其差值，本例中共64對，輸出超過30頁。為了有選擇性地比較處理組合間的均值差異，需要將上述語句進行替換。如要比較date1(1月24日)與date2(1月24日)的產量差異，即需要替換為“Lsmestimate variety*date ′date1 vs date2 in variety1′ 1 -10;”；要以variety1 date1(翠碧1號，1月24日移栽)為對照進行產量差異比較，則需替換為“Lsmeans variety*date /diff = control (′1′ ′1′);”；要比較品種1(翠碧1號)與所有其他3個品種平均產量的差異，則需替換為“Estimate ‘variety1 vs others’ variety -3 1 1 1 /divisor =3;”。

1.3.3用MIXED程序模塊進行F檢驗和均值比較 SAS的MIXED也可用來進行裂區設計的方差分析。進行F檢驗時，class、model、random、lsmeans語句的用法與GLIMMIX的完全相同，F檢驗和均值比較的程序如下。

PROC MIXED data = split;

Class block variety date;

Model yield = variety date variety*date/ddfm=satterth;

Random block block*variety;

Lsmeans variety date variety*date /diff;RUN;

2 結果與分析

2.1 運用GLIMMIX模塊進行F檢驗、多重比較及交互作用比較

運行程序1，得 到F檢驗的主要結果見表2。可以看出，烤煙產量主區因子品種間、副區因子移栽期之間，以及他們的交互作用效果都達到極顯著水平(P<0.001)。因此，有必要分別對各處理組合的產量均值差異進行比較。受篇幅所限，僅列出部分處理組合間的產量均值差異(表3)。其中，第1行數據表示variety1(翠碧1號)，在date1(1月24日)移栽的烤煙產量比在date2(1月31日)移栽的極顯著地高出780 kg·km-2(P<0.001)。

表2 F檢驗結果(Ⅲ型)Table 2 Output of F test (Type Ⅲ SS)

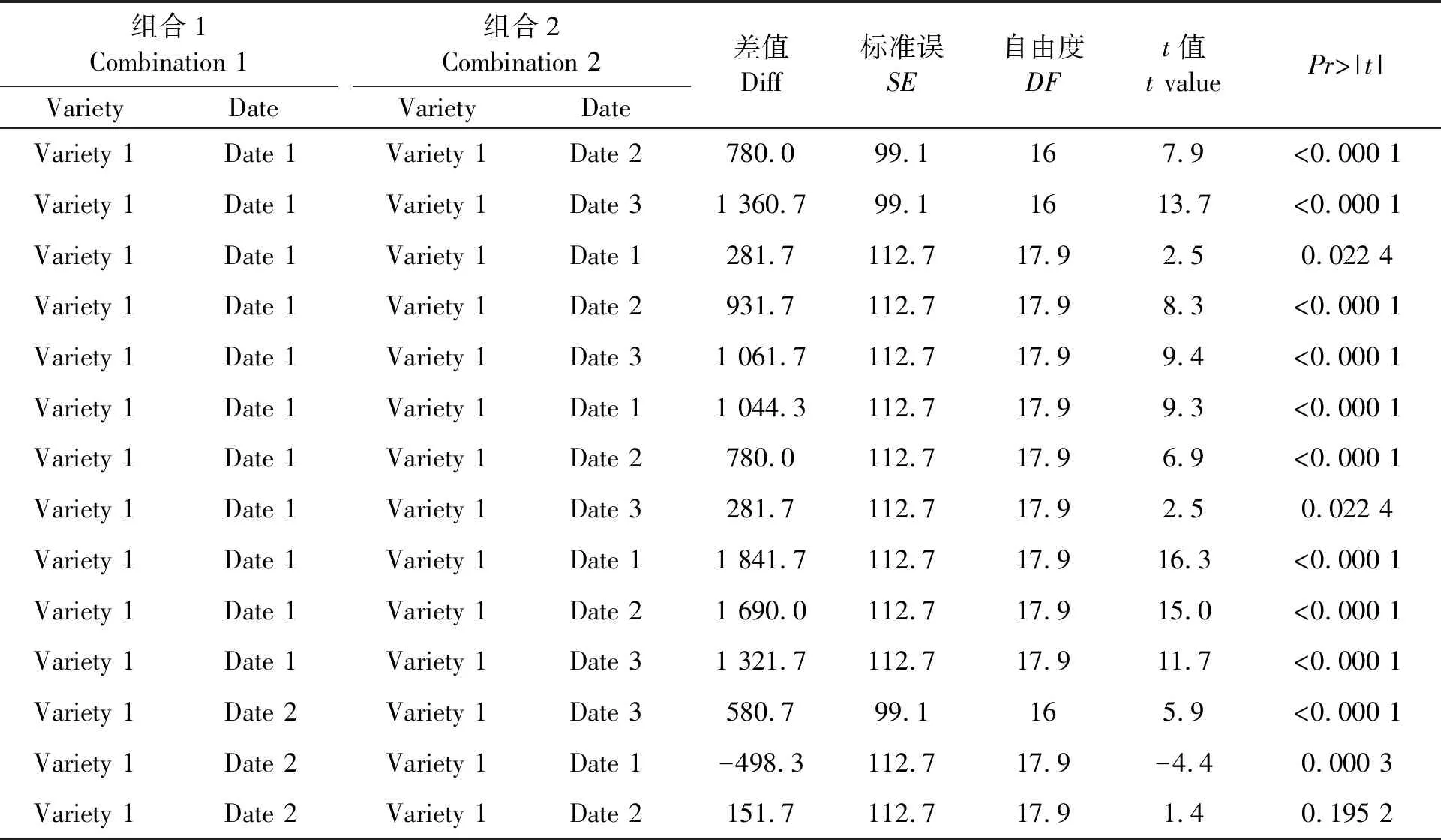
表3 部分處理組合的產量均值差異比較Table 3 Difference comparison of mean yield between part treatment combinations

品種和移栽期的交互作用效果圖見圖1，可以看出，各品種烤煙產量隨不同移栽期處理的變化趨勢明顯不同，variety1、2隨移栽期的推遲，產量下降；variety3、4隨移栽期的推遲，產量增加。在date1(1月24日)移栽時，variety1產量最高，variety4最低；而在date3(2月8日)移栽時，品種1產量最低，品種3最高。如果品種和移栽期處理間的交互作用不存在，這些線將呈現平行趨勢。

綜上，結合均值比較結果(圖1)能夠很容易地確定產量最高的最佳處理組合，即最佳移栽期為date1(1月24日)的variety1(翠碧1號)。從表3的第1、2行可以看出，variety1的date1組合與variety1的date2組合，及variety1的date1組合與variety1的date3組合差異均為極顯著水平。因此，variety1(翠碧1號)的最佳移栽期為date1(1月24日)。

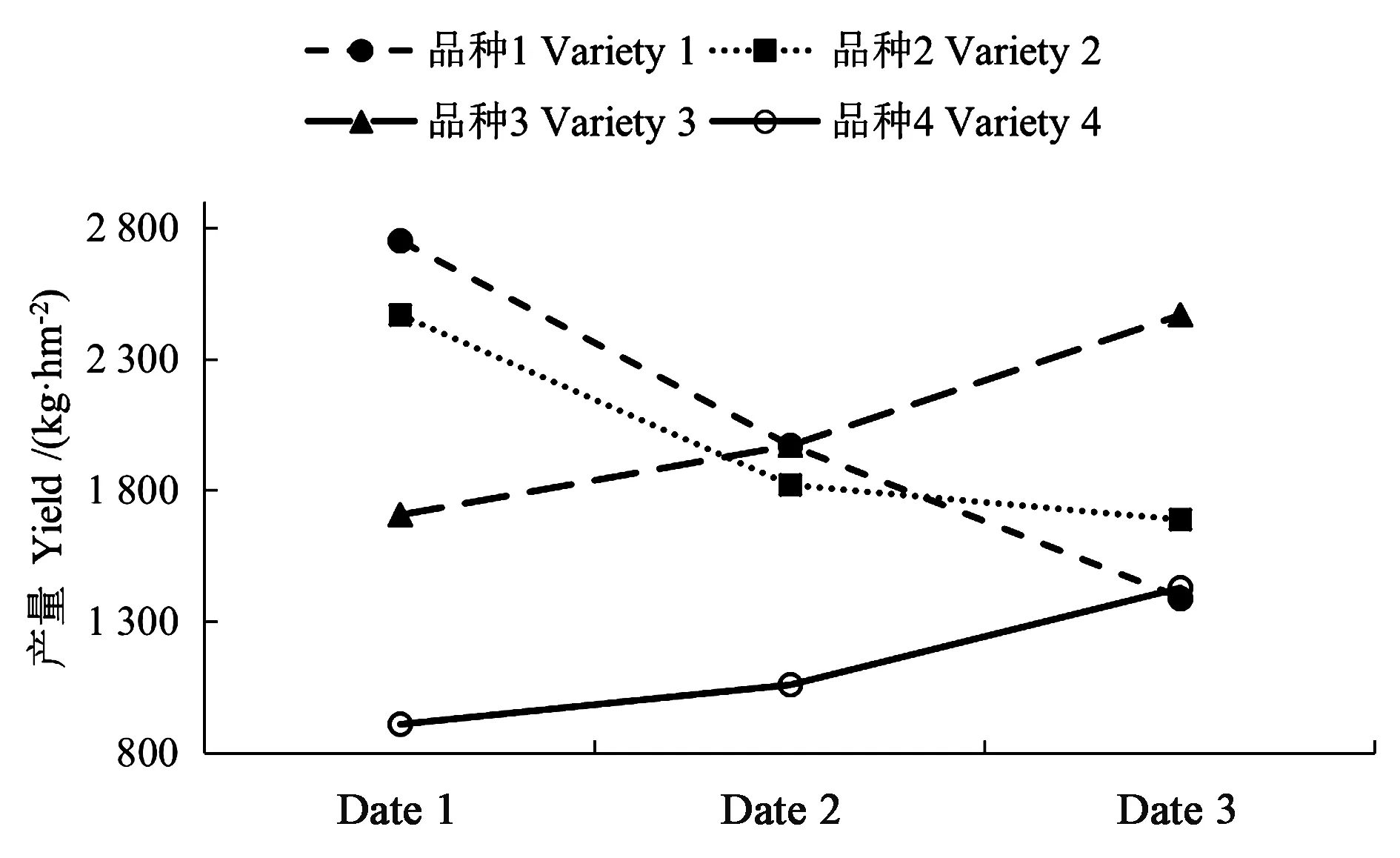
圖1 品種與移栽期交互作用Fig.1 Profile of interaction between variety and date

為了進行方法說明，現假定品種與移栽期的交互作用效果不顯著，即假定表2中的variety*datePr>F大于0.05，即品種的產量效果不受移栽期的影響，同時移栽期的產量效果與品種無關，此時的均值比較僅需對品種和移栽期分別進行。用Lsmeans variety/diff比較品種間的均值差異，結果見表4。可見，綜合3個移栽期的平均產量結果，variety1、2、3與4的產量差異達到極顯著水平，而其他品種間無顯著差異。用Lsmeans date/diff 比較不同移栽期產量之間的均值差異，結果見表5。可見，綜合4個品種的平均結果，date 1與date2和3的產量差異均達到極顯著水平，而date2與date 3間無顯著差異。需要特別說明的是，這種均值比較只有在品種與移栽期交互作用效果不顯著的前提下才能進行，否則沒有意義。

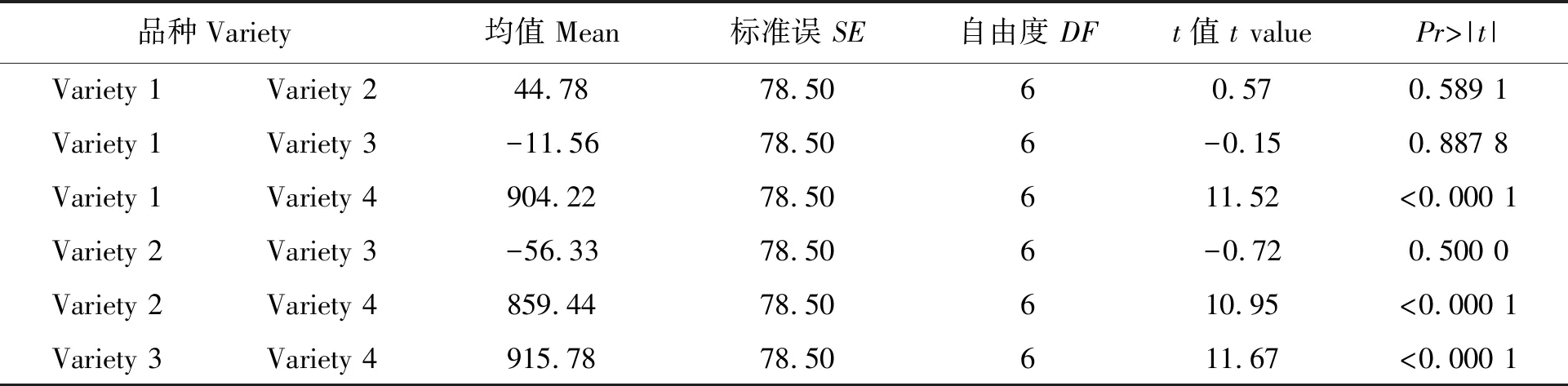
表4 各品種間產量差異顯著性(所有移栽期平均)比較示例Table 4 Example of mean difference between varieties across all of the dates

表5 各移栽期間平均產量的差異顯著性示例Table 5 Example of mean difference of yield between dates across all varieties

2.2 部分處理組合間的均值比較結果

為了節省輸出文檔的篇幅，避免產生大量不必要的輸出，可以進行某些特定均值間的差異比較，如1.3.2 中語句“Lsmestimate variety*date ′date1 vs date2 in variety1 ′ 1 -10;”的輸出結果見表6，可以看出， date1(1月24日)與date2(1月31日)的產量差值為780.0 kg·hm-2，與表3中date1(1月24日)與date2(1月31日)的產量差值相同。說明語句“Lsmestimate variety*date ′date1 vs date2 in variety1 ′ 1 -10;”的作用與“Lsmestimate variety*day”是相同的，但該語句的輸出內容更簡潔。

表6 Lsmestimate 輸出示例Table 6 Example output of Lsmestimate

3 討論

在進行裂區設計的方差分析時，通常采用ANOVA或GLM程序模塊[1, 5, 17-18]。由于主、副區處理需要采用不同的誤差方和及自由度，ANOVA或GLM缺乏內置程序進行自動處理，某些情況下需要手工計算，大大增加了計算量和難度[1]，且容易出錯。本研究采用GLIMMIX程序模塊能恰當地解決這些問題，即使是非平衡設計(如各處理組合的重復次數不等或缺區)的情況。

本研究采用的實例數據與孫久權等[1]的實例數據完全相同，而孫久權等[1]采用GLM進行統計分析，程序繁雜，如其在計算variety處理效應(主區因子效應)的F值時，SAS的默認方法有誤，需要通過語句"Test h = replicate variety e = replicate*variety”進行修正，才能得到更準確的、與采用GLIMMIX程序模塊相同的F值(64.92)。MIXED和GLIMMIX能夠區別對待固定效應和隨機效應變量，在Model語句中，只需列出固定效應變量即可，如本研究中可以采用以下語句。

Model yield = variety date variety*date / ddfm = satterth;

Random block block*variety;

而GLM程序模塊的model語句需要列出所有變量，如孫久權等[1]的model語句如下(replicate與block等同)。

Model yield = replicate variety date replicate*variety variety*date;

Test h = replicate variety e = replicate*variety;

為了正確計算主區因子的F值，GLM程序模塊需要使用Test語句。類似地，使用LSMeans進行主區因子間的差異比較時，必須單獨指明誤差項，即“LSMeans variety/ e = replicate(variety) stderr, tdiff;”；否則GLM程序模塊將默認使用副區誤差項計算t值。

在MIXED和GLIMMIX程序模塊中，只要在random語句中列出隨機效應項，如本研究中的“Random block block*variety”，SAS在計算F和t值等統計量時，就會根據適當的方差結構，自動選用恰當的誤差項方和與自由度等，這是GLIMMIX程序本身事先內置的功能。GLM缺乏該內置功能，需要列出誤差項，即使使用random語句也不能實現。然而，有些情況下，GLM程序模塊缺乏此內置誤差項，因而GLM不能自動計算該統計量[15,19-20]。此外，GLIMMIX程序模塊可以方便地輸出交互作用效果圖(圖1)，但GLM和MIXED無此功能。

雖然GLIMMIX模型在分析裂區設計試驗數據時，優勢很多。但是，GLIMMIX模型是基于線性混合模型進行迭代的[20]，不能用于嵌套模型的比較，且允許殘差方差及不同協方差結構的類型有限[21]，由于PROC GLIMIX對隨機效應的標準誤估計有偏差，因而不能用于隨機效應的顯著性檢驗。

在GLIMMIX進行裂區設計試驗數據分析時，仍有一些要點需要注意。本研究程序1用ddfm=satterth對標準誤、自由度等進行校正，以保證F值的正確性。Kenward和Roger[17]用“ddfm = kr”來修正標準誤、自由度、檢驗統計量等的計算，所得結果的準確性得到進一步提高。如果裂區設計為平衡設計，satterth和kr效果完全相同；如果為非平衡設計或存在缺區，尤其是在重復測量和空間相關的情況下，二者有本質區別，推薦使用kr。在輸出交互作用圖時，本研究將變量date視為分類變量，所以x軸為等距。如果x軸要按比例顯示，需要采用Gplot程序作圖。如果要將variety設為橫坐標，可用sliceby= date 代替sliceby=variety 選項。程序1的輸出不含某些均值比較。例如，檢驗品種1與所有其他3個品種平均產量的差異顯著性時，可以通過estimate、contrast或lsmestimate語句后的系數來實現，語句為“Estimate ‘variety1 vs others’ variety -3 1 1 1 /divisor =3;”。其中，系數的順序一定要與程序1中class語句的變量順序一致，即variety在date之前。本研究中，各品種的產量與date存在直線或曲線關系(圖1)。因此，可以以移栽期為自變量，產量為因變量進行回歸分析，建立產量與移栽期的回歸方程，用以預測產量，具體可采用SAS的REG、MIXED等模塊進行擬合和統計檢驗。

在MIXED模塊中，SAS使用限制最大可能性估計(REML)或ANOVA方式進行方差分量，默認方式為REML。若采用ANOVA進行估計，語句為“PROC MIXED data = split method = type3”。對于平衡設計，REML與ANOVA結果相同，但ANOVA能夠輸出更詳細的方差分析結果。在進行均值比較時，GLIMMIX模塊可采用estimate、contrast或lsmestimate語句。但lsmestimate語句是針對GLIMMIX模塊開發的，MIXED模塊不能使用。然而，estimate、contrast語句的寫法較繁瑣[19]，SAS公司對其進行了簡化，變為lsmestimate，寫法更加簡便[20]。