撥動擴散思維之弦 探究數學奇幻之美

郝云鳳

摘要

桑代克的效果律認為，學習數學需要做一定量的題目，以讓學習效果展現出來。但教師要指導學生一題多想，一方面避免不必要的題海戰，另一方面也讓學生的思維品質得到提升，具體來說就是要提升思維的邏輯性、深刻性、獨立性、靈活性、敏捷性和批判性，尤其是讓擴散思維得到發展，進而使學生喜歡上數學，發揮其主動性，探究數學奇幻之美。

關鍵詞

初中數學 一題多想 擴散思維

當前的初中數學教學存在著學生做題目的時間多，想題目的時間少這樣的問題。換言之，就是學生只是在埋頭做題，沒有真正地去思考與題目相關的一系列問題。這樣的模式會導致學生做了許多題目，卻不知道題目的內核是什么，在遇到新的題目的時候，不能從做過的題目中汲取方法與思路。因此，教師要加強解題教學中的過程性引導，幫助學生的思維品質在一題多想的過程中得到改善，在學習上達到事半功倍的效果。提升思維的邏輯性，思考題目之間的聯系;提升思維的廣闊性，思考更多的思路;提升思維的深刻性，思考問題的內核是什么;提升思維的獨立性，思考這道題目的不同之處在哪兒;提升思維的靈活性，思考有沒有更多的解法;提升思維的敏捷性，思考有沒有更簡單、更快捷的方法;提升思維的批判性，思考別人做題的優點與不足。

一、培養學生的生活意識

數學與生活總是有一定聯系的，在生活中隨處可見數學的影子，在數學原理與公式中也能發現生活中的例子。在數學教學中，要讓學生將題目與生活聯系起來，從而讓他們的思維得到轉化，將抽象思維轉化為形象思維。因此，在學生遇到某一題目時，要讓他們多想一想生活中有沒有相似的情境。當學生能將題目融入生活，他們就會對題目多一份親切感，少一份生疏感，進而更容易想出解決的路徑。學生將題目和生活聯系起來，在某種意義上也說明他們看懂了題目。

以實際問題與一元一次方程等相關問題為例，筆者設置了這樣一道題：某地的A、B兩家工廠急需煤90噸和60噸，該地的C、D兩家煤場分別有100噸、50噸，全部調配到A、B兩家工廠，已知C、D兩個煤場運到A、B兩家工廠的運費（元/噸）如下表所示：

運送完畢后，A、B兩家工廠共付運費5200元，問煤場C、D各有多少噸煤運往A工廠。對于這樣的題目，學生很快就能想出解題的思路。他們先設C運給A廠x噸，那么C運給B廠就是（100-x）噸，D運給A廠就是（90-x）噸，D運給B廠就是（x-40）噸。同時他們由題意得出35x+40（90-x）+30（100-x）+45（x-40）=5200，進而求得x=40，所以煤場C、D有40噸和50噸煤運往A工廠。

解答完這樣的題目，學生就在想：這不就是用數學來解決生活中的問題嗎？生活中像這樣的例子不是還有很多嗎？教師再引導學生想一想生活中有沒有數學的影子，其實就是通過生活實際將數學中的認知以更直觀的方式展示出來，這也是解決數學問題的一種有效方式。

二、培養學生的問題意識

在預習的過程中，教師問什么問題學生就思考什么問題，將相關的問題弄懂，預習也就結束;在互學的過程中，教師會拋給學生一些問題，他們會圍繞問題展開討論，以得出一些結論;在展學的過程中，教師會設置一些問題，讓學生將認知轉化為解題的能力，提升素養。明顯地，在這種模式下，教師成為課堂的主體，掌控著整個課堂的節奏，學生只是在被動地接受。在數學教學的過程中，讓學生去發現問題，比解決問題更重要。學生去發現問題，首先，要有一定的識記能力，要能記得相關的原理與定律;其次，需要一定的推理能力，即由這些定律會發現題目中存在的問題;最后，還要有一定的分析能力，即要分析這些問題是否真的成立，并找到解決方案。因此，在解答一道題之后，教師可以讓學生的思維保持繼續發展的態勢，讓他們想一想有沒有新的問題。

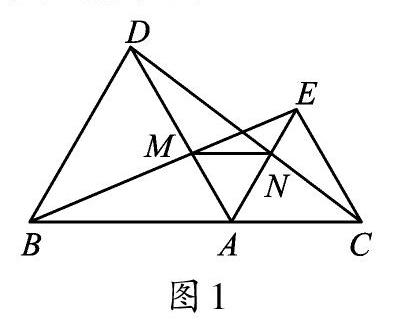
在學習等邊三角形的相關知識時，筆者設置了這樣一道題：點4是線段BC上一點，△ABD、△AEC都是等邊三角形，BE交AD于點M，CD交AE于點N，如圖1所示。求證：BE=DC。

對于這樣的問題，學生很快就能想到，因為△ABD、△AEC都是等邊三角形，所以AD=AB，AC=AE，∠DAB=∠CAE=60°。有了這些結論，他們就能通過列舉條件，進而證得△DAC≌△BAE（SAS），所以就有了BE=DC。之后，筆者引導學生繼續觀察圖形，發現題目中給出的條件能得出更多的結論。他們試著證明△AMN是等邊三角形，先是利用△DAC≌△BAE這一結論，得出∠ABM= ∠ADN;再從已知條件推出的∠BAD=∠EAC=60°中得出∠DAN=60°;然后又由AB=AD，得出了△ABM≌△ADN（ ASA），進而有AM=AN，同時又因為∠MAN=60°，證得△AMN是等邊三角形。

學生充分利用條件和新結論的過程，就是他們思維向縱深發展的過程。讓學生多想問題，一方面教師能更直觀地看出學生思維的特點，再為他們制定更好的教學方案;另一方面學生能更主動地投入到課堂中來，成為課堂的設計者，而不僅僅是一個聽眾。

三、培養學生的關聯意識

在教學的過程中，我們經常會遇到這樣一種情況，一道題講了很多遍，學生在做題的時候還是會出錯。可是在這些做錯的學生當中，有許多在聽講的時候，是明白做題思路的。可為什么換道相似的題，他們就出問題了呢？這其中一個主要的原因就是學生在做題的過程中缺少思考的過程，即沒有去思考有沒有做過相似的題。他們沒有從做過的題目中找尋經驗和靈感，將相關認知聯系起來。

每道題的出現都不是孤立存在的，從做過的題目入手，能更快地喚醒曾經的思路，找到解題方法。例如下面這道題。如圖2，已知AB是○O的直徑，AC是○O的切線，連接OC交○0于點D，連接BD。若∠C=40°，則∠B=____。

按照通常的思路，教師會問：因為AC是○0的切線，所以我們能得出什么結論呢？學生會答：OA⊥AC，∠OAC=90°，∠AOC=90°-∠C=90°-40°=50°。教師再問：因為OB=OD，又能得出什么結論呢？學生答：∠OBD=∠ODB。同時他們還會補充說，因為∠AOC= ∠OBD+ ∠ODB，所以∠OBD=1/2∠AOC=25°，即∠ ABD的度數為25°。這樣的教學模式，只是就題論題，學生的思維沒有往更廣闊的領域發展。教師可以引導學生將以往做過的題目聯系起來，既觸類旁通，又彼此補充，不斷深化。

學生翻看各種講義，他們發現這樣一題：如圖3，AD是○0的弦，AB經過圓心O，交○0于點C，∠DAB=∠B=30°，問直線BD與OD形成的角是否為90°。學生發現此題同樣是運用有關切線的認知求某一角的數值，在解決過程中同樣需要將角度之問的數值進行轉換。連接OD，由∠ODA= ∠DAB= ∠B=30°，得∠ODB=180°-∠ODA-∠DAB-∠B=180°-30°-30°-30°=90°。可見讓學生回想做過的題目，能在鞏固認知的同時，進一步深化思維。

經過筆者的教學實踐，學生學會了自我“搭橋造船”去解決問題，一題多想，舉一反三，提高了學習效率。當然，筆者在教學反思中也發現了一些需要改進的地方。例如，要結合學生實際能力，循序漸進地訓練學生這方面的能力，不能急于求成;不能兩極化，學生的練習量要適度保證。

學生才是數學學習過程中最需要關心的主體。因此教師在教學中要時刻關注學生的學習過程，讓他們得到最大限度的發展。讓學生一題多想，既是在減輕學生的學習負擔，又是在提升他們的思維品質和擴散思維能力。在尊重學生身心健康的同時，給予他們最適切的教育，從而讓學生喜歡上數學，發揮其主動性，探究數學的奇幻之美。

（作者單位：江蘇省南京江寧濱江外國語學校）

【參考文獻】

[1]陳美清，淺談初中數學解題教學中學生思維品質的培養[J].江西教育學院學報，2012（3）.

[2]張亞紅，巧用一題多解培養學生的創造思維[J].甘肅教育，2018（ 14）.

[3]王婧，初中數學解題思路的教學方法探究[J].天天愛科學（教育前沿），2020（5）.

[4]唐妙英，引導學生解題后反思，讓數學思維繼續飛翔[J].課程教育研究，2020（3）.

[5]李小磊，初中學生數學思維品質的優化[J].數學大世界（上旬），2020（4）.