諧波減速器禮帽形柔輪應力應變分析與參數優化*

（江蘇科技大學 鎮江 212000）

1 引言

自1965年美國工程師Musser發明了第一代諧波減速器以后，諧波減速器就開始投入了實際應用［1］。與傳統減速器相比，諧波傳動具有精度高、結構緊湊、重量輕、減速比高和傳動精度高等特點，使其被廣泛應用于航天航空、機器人、精密機床、儀器儀表等領域［2］。由于行業的發展，各領域對諧波減速器的要求越來越高，諧波減速器軸向尺寸的減小，使得柔輪所受的應力急劇上升。而諧波減速器主要失效形式就是柔輪的破壞，由于柔輪齒圈結構上的非線性以及柔輪變形上的非線性，所以一直以來也無法精確計算柔輪在波發生器作用下產生的應力［3］。

隨著有限元技術的發展，許多學者借助有限元軟件總結了柔輪的應力應變規律。邢靜忠利用有限元技術發現了禮帽形柔輪相較于杯形柔輪，負載工況引起的等效應力增幅更?。?］。彭盼道利用有ANSYS Workbench和正交試驗法優化了柔輪雙圓弧齒形的參數［5］。張世民利用ANSYS得出了不同負載對短杯柔輪的應力位置影響不大［6］。鄧娟利用有限元得到柔輪厚徑比和筒體長度對柔輪的影響規律，然后利用Matlab對試驗數據進行曲線擬合，證明了理論計算的正確性［7］。

目前對于諧波減速器柔輪的研究主要集中在短杯形柔輪，而對禮帽形柔輪的研究不多。隨著行業的發展，諧波減速器負載要求的提升，禮帽形柔輪在負載增加的情況下所受應力的增幅遠遠低于杯形柔輪的增幅［8］，這對柔輪的壽命和穩定性有著至關重要的影響，所以禮帽形柔輪更適合在大負載工況下的應用。但是禮帽形柔輪的空載情況下的應力遠大于杯形柔輪，所以對禮帽形柔輪空載時的應力研究十分必要。

2 柔輪有限元分析

2.1 柔輪與波發生器幾何模型

禮帽形柔輪結構圖簡圖，如圖1所示?，F以工程中某型號柔輪為分析對象，其幾何參數：筒長l=21.1mm，柔輪筒壁厚h0=0.37mm，覆板厚度h=0.37mm，筒內半徑r0=16.95mm，d0=2r0=-33.9mm，筒底與覆板過渡圓角半徑r1=1.78mm，柔輪輪齒寬b=7mm。

圖1 禮帽形柔輪結構簡圖

本文波發生器選用橢圓波發生器，根據文獻［7］橢圓波發生器的計算公式：

式（1）和式（2）中a1、b1分別為橢圓的長半軸和短半軸，W0是最大徑向變形量，本工程實例中最大徑向變形量為一個模數m=0.219。

2.2 應力應變計算

采用SolidWorks軟件對柔輪和波發生器進行三維建模，然后將模型導入到ANSYS Workbench16.0有限元軟件中進行計算。根據實際工程實例，柔輪的材料為40CrNiMoA合金結構鋼，彈性模量為209GPa，泊松比0.295；波發生器的材料為40Cr，彈性模量為211GPa，泊松比為0.277。ANSYS Workbench中剛體為目標面（target），可變形面為接觸面（contact），所以我們這里設置波發生器外圈為目標面，柔輪內圈為接觸面；覆板底面施加固定約束，波發生器內孔施加軸支撐約束。在幾何上，柔輪的最大徑向變形量與厚度之比大于0.2，屬于大撓度幾何非線性問題［9］，所以需要在分析設置中打開大變形和弱彈簧選項，采用拉格朗日算法求解。覆板底面施加固定約束，波發生器內孔施加軸支撐約束。有限元模型如圖2所示。

圖2 禮帽形柔輪有限元模型

3 柔輪應力應變分析

3.1 柔輪應變分析

3.1.1 軸向應變分析

為了研究柔輪軸向應變的變化規律，我們選取了波發生器長軸、短軸以及長短軸之間45°處三個位置來觀察它們的軸向應變。其結果如圖3所示。

圖3 軸向應變分布圖

圖3中橫坐標為距離齒圈前緣的距離，齒圈前緣位置如圖2中所示。從圖3中可以看出，最大變形出現在波發生器長軸與柔輪接觸處，最大形變量為0.275mm。并且軸向應變與距離齒圈前緣距離成線性規律，這與文獻［9］中的試驗結果是一致的。并且從圖3中可以看出波發生器長軸處柔輪的變形量大于短軸處柔輪的變形量大于長短軸之間45°處柔輪的變形量。

3.1.2 徑向應變分析

本文選取了如圖2中所示的齒圈前緣處、筒底倒角處以及柔輪筒與齒間過渡處這三個位置來研究柔輪徑向應變的。如圖4所示，柔輪徑向應變分布呈現規則的花瓣狀。柔輪三處最大變形量均出現在與波發生器長軸接觸的地方，最小變形量出現在波發生器長軸與短軸之間，齒圈前緣變形量大于筒齒過渡處變形量大于筒底倒角處變形量。

圖4 柔輪徑向應變分布

3.2 柔輪應力分析

3.2.1 軸向應力分析

接著我們對柔輪的應力進行分析，圖5為柔輪軸向應力分布圖，和分析應變一樣，選取了波發生器長軸、短軸以及長短軸之間45°處三個位置來觀察它們的軸向應力。從圖5中可以明顯地看出，柔輪三個位置等效應力均集中在齒圈前緣和筒底倒角處，筒底倒角處應力最大。波發生器長軸位置距離齒圈前緣5mm處應力發生波動是由于與波發生器接觸導致的應力集中。齒圈前緣應力集中是由于柔輪受波發生器影響被迫擠壓變形，齒圈前緣變形量大，導致應力集中，短軸處齒圈前緣的應力是三個位置中最大的。

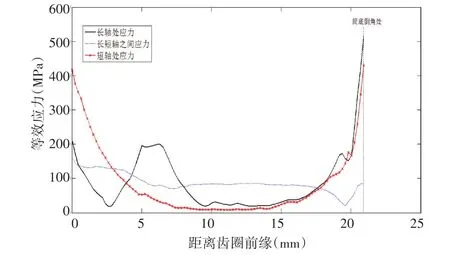
圖5 柔輪軸向應力分布圖

3.2.2 徑向應力分析

從分析軸向應力分布圖中可以知道柔輪應力主要集中在齒圈前緣和筒底倒角處，于是我們選取這兩個位置處的截面并觀察對其徑向上應力變化規律，這兩個位置的徑向應力分布圖如圖6所示。從圖6中可以清楚的看出最大等效應力出現在波發生器長軸筒底倒角位置，其值為538.52MPa。在波發生長軸方向周圍，筒底倒角應力普遍大于齒圈前緣應力。而在波發生器短軸方向周圍，齒圈前緣處應力普遍要大于筒底倒角處應力，但是波發生器短軸方向上最大應力仍然出現在筒底倒角處。

圖6 柔輪徑向應力分布圖

將工程實例中的樣機與有限元模型進行對比，工程實際中的柔輪失效情況如圖7所示。從圖7中可以看出，樣機柔輪在筒底與覆板過渡處發生斷裂，這與有限元計算結果一致。

圖7 禮帽形柔輪樣機失效圖

4 柔輪結構參數優化設計

4.1 正交試驗設計

正交試驗設計是研究多因素多水平的一種設計方法，能根據正交性從全面試驗中挑選出部分代表性的點進行試驗，從中挑選出最優水平組合，是一種高效率、快速、經濟的試驗方法［11］。

此次試驗，以降低禮帽形柔輪所受最大應力為目標，進行正交試驗設計，分析長徑比l/d0，齒寬b，覆板厚與柔輪壁厚比h/h0，以及筒底與覆板過渡處圓角半徑r1的大小對柔輪最大應力的影響。基于不改變柔輪內徑的原則下，根據文獻［12］中所述，選取每個因素的3個水平，采用四因素三水平，試驗如表1所示。

表1 四因素三水平表

四因素三水平表選用L9（34）型正交試驗表，一共9組試驗，如果不用正交試驗，將各水平試驗全做完需要81次試驗，大大減少了工作時間。

4.2 正交試驗結果處理與分析

根據正交實驗表中所給出的試驗方案，選取方案中的水平組合，在SolidWorks中建立九個試驗中新的禮帽形柔輪幾何模型，因為這里的因素是在柔輪內徑不變的原則下選取的，所以波發生器的幾何模型不需要改動。再將新的幾何模型分別導入到ANSYS Workbench中進行有限元分析，得出每組試驗的最大應力，試驗結果如表2所示。

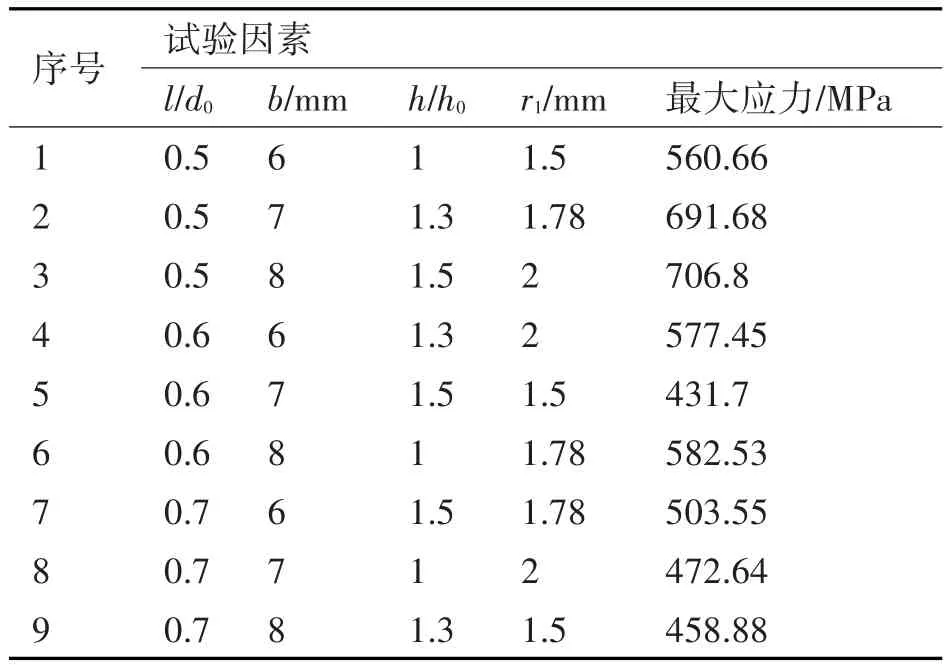
表2 正交試驗表

從表2中可以看出第五組試驗最大應力比第二組試驗應力值減小了275.1MPa，差距十分大，由此可見結構參數優化的必要性。接下來我們對試驗結果采用直接分析法進行分析，就可以得出最佳的水平組合。首先需要計算各因素各水平的平均值Ij，再分別計算各因素平均值的極差Rj，根據極差可以判斷各因素對試驗結果的影響大小，平均值和極差的計算如表3所示。

表3 正交試驗結果表

由表三可知長徑比l/d0的第三個水平I3應力值最小，齒寬b的第二個水平I2應力值最小，覆板厚與柔輪壁厚比h/h0的第一個水平I1應力值最小，筒底與覆板過渡處圓角半徑r1的第一個水平I1應力值最小。本試驗中選取最優水平解為l/d0取0.7，b取7mm，h/h0取1，r1取1.5。將試驗最優解進行模型創建和有限元求解，參數優化后的柔輪最大應力變為了411.21MPa，比原來的工程實例樣機最大應力減少了23.64%。

5 結語

禮帽形柔輪最大應變出現在波發生器長軸與柔輪接觸處；波發生器長軸處柔輪的變形量大于短軸處柔輪的變形量大于長短軸之間柔輪的變形量；齒圈前緣變形量大于筒齒過渡處變形量大于筒底倒角處變形量。

禮帽形柔輪等效應力集中在齒圈前緣和筒底倒角處，最大等效應力出現在波發生器長軸方向上的筒底倒角處；波發生器短軸方向上，齒圈前緣應力集中較大。

禮帽形柔輪的結構參數的不同水平組合產生的最大應力極差較大，可以通過優化尺寸結構，來降低柔輪最大應力。

通過正交試驗，降低了工程實例中的柔輪參數從l=21.1mm、齒寬b=7mm，覆板厚度h=0.37mm，筒底與覆板過渡圓角半徑r1=1.78mm，修改至l=23.73mm，齒寬b=7mm，覆板厚度h=0.37mm，筒底與覆板過渡圓角半徑r1=1.5mm，應力值從538.52MPa將至了411.21MPa，降低了23.64%，使柔輪的性能得到了很大的改善。

禮帽形柔輪的長徑比以及筒底與覆板過渡圓角半徑是最大應力的敏感因素，在工程設計中需要著重注意，齒寬和覆板厚度并不是禮帽形柔輪的最大應力的敏感因素。