國際產業轉移對各國碳排放的影響研究
——基于多區域投入產出模型

董 聰 王 晨 董秀成

（1.對外經濟貿易大學國際經濟貿易學院，北京 100029；2.博科尼大學經濟系，米蘭 I-20136）

一、引言

20世紀80年代以來，經濟發展的迅猛態勢和貿易全球化的興盛深刻地改變了世界經濟面貌，貿易分工和跨國生產已經成為世界經濟發展的主要推動力（Hummels等，2001）。[1]許多國家積極參與世界分工，借由經濟全球化的浪潮迎來了本國發展的良好機遇。然而日益凸顯的一系列環境問題也伴隨經濟發展而來，氣候變化問題甚至威脅到了人類的生存和發展。二氧化碳的控制減排已不再是簡單的科學議題，而是成為了各國發展所要角力的重要環節。當發展中國家參與全球分工，成為國際產業轉移的目的地時，部分學者針對這一現象提出污染避難所假說（Walter，1979），[2]即認為污染密集型產業會從環境規制水平高、排污成本高的發達國家流向規制水平低、排污成本低的發展中國家，從而使發展中國家成為轉移污染的避難所。加之國際環境有關提議的主要目標基本都是以生產過程的排放為核算對象，從而使得產品進口國滿足自身消費需求的同時，又避免了二氧化碳等溫室氣體的減排責任，因此國際間產業轉移無疑會加劇東道國的碳排放總量。另一部分學者卻持不同意見，他們認為由于伴隨著產業轉移存在技術“外溢效應”，產業轉移不一定會引起碳排放的增加。如Antweiler等（2001）從一般均衡視角研究貿易對污染排放的影響，認為技術水平的提升會抑制貿易產生的污染，得出進行國際貿易對環境有利的結論。[3]

以我國為例，改革開放以來，尤其是加入WTO之后，中國迅速融入世界經濟體系，參與國際分工，在一段時間內一直被冠以“世界工廠”的稱號，在世界經濟中扮演者越來越重要的角色。與此同時，中國的二氧化碳排放量在2008年正式超過美國，躍居世界第一位。在碳達峰和碳中和目標下，中國面臨的減排壓力也與日俱增。由于接納了國際間能耗較高、污染較重的產業，高污染、高能耗產品占據了相當部分的出口貿易份額，中國贏得貿易順差的同時，也排放了大量污染物，為其他國家背負了碳排放壓力。

避免國界或者關境對減排政策的割裂，對全球每個國家、每個部門的碳排放進行深入研究，以全面了解碳排放的增長和影響因素尤為必要（趙忠秀等，2018）。[4]本文借鑒了隱含碳研究中的多區域投入產出模型，核算各國與部門碳排放，而后對碳排放進行結構分解，將由國外因素（包括國外需求因素和國外技術因素）所拉動的碳排放增加值剝離出來，探究其與各個國家在世界范圍內產業轉移的關系和影響，希望將國際產業轉移的影響通過本國碳排放體現出來，以期為政府相關部門在環境治理、節能減排及產業轉移和承接方面提供政策參考。

本文的創新之處在于：首先，部分已有文獻在研究碳排放與貿易、產業間的關系時，以一國碳排放總量來進行探究，將本國需求、技術原因所拉動的碳排放增量與國外原因所帶動的碳排放增量分離開來，更精確地對外部原因進行定位。其次，由于技術溢出效應帶來的產業減排，許多產業轉移與環境污染領域的研究受到不同程度的干擾，隨著產業轉移而來的節能減排技術能否對本國碳排放產生影響，如果產生影響，效應又如何衡量，本文采用SDA分解法將國外因素中的技術影響剝離開來，使其后的實證數據更加可靠，并由此對技術轉移的影響進行量化探究。此外，為進一步驗證回歸結果的可靠性，本文從三個角度設置不同的假設，通過穩健性檢驗，模型結論的有效性得到證實。最后，將不同年份的投入產出表進行比較分析，以動態視角反映社會生產中需求、技術的變化過程，模型所采用數據均為基期與報告期的變化值，因此在數據的規范性和穩定性上具有一定的優勢。

二、文獻綜述

在近年來關于碳排放的研究中，隱含碳排放已成為研究熱點（張中華等，2019），[5]本文對隱含碳排放模型多有借鑒。當前針對隱含碳的核算方法主要有三種：直接排放核算法、基于完全需求系數測算法以及基于完全消耗系數測算法（王媛等，2012）。[6]除第一種外，其余兩種都屬于投入產出分析法，這一分析方法由里昂惕夫在20世紀三十年代提出，通過投入產出表的編制及相應模型的建立，投入產出法可以用來反映經濟體中多個部門的產業間相互關系。在能源、環境的相關研究中，它常被用來追蹤產品的全部能源消耗及二氧化碳排放量，是宏觀視角下研究經濟體碳排放的主流方法。

在針對某一個國家的研究中，單區域投入產出模型（Single Regional Input-Output Model）常被用來對該國碳排放情況進行測算。朱啟榮（2010）藉由中國2002年和2007年投入產出表對出口貿易活動產生的二氧化碳排放量進行了測算，同時對我國出口貿易結構所存在的問題進行了分析。[7]鄧榮榮（2014）基于非競爭性可比價投入產出表，對我國1997-2011年碳排放情況進行了測算，結果顯示出口含碳量的增長速度高于進口含碳量。[8]除了單區域投入產出模型，也有學者運用雙邊投入產出模型（Biregional Input-Output Model）來對兩個國家或區域的貿易情況進行研究，以探尋環境或二氧化碳排放問題。Bin和Robert（2006）定量測算了1997-2003年美國出口到中國商品中的隱含碳排放量。[9]王菲等（2012）通過雙邊投入產出模型分析了中日間貿易的碳排放情況，結果顯示中國為日本承擔了巨大的消費型隱含碳排放。[10]然而，在世界多個國家深度參與貿易全球化的背景下，雙邊投入產出模型自身容易存在不可避免的誤差，因此多區域投入產出模型（MRIO）在多個國家或地區貿易隱含碳排放的研究中備受學者歡迎。龐軍（2014）基于GTAP數據庫建立MRIO模型，對中歐二氧化碳排放量以及行業排放分布進行量化，發現中國是典型的隱含碳排放凈出口國，歐盟則相反。[11]為了利用世界范圍內的樣本來探討碳排放隨產業的轉移，本文采取基于完全消耗系數測算法的多區域投入產出模型。

近年來經濟生產中二氧化碳的排放問題日益受到各國政府重視，國內外學者對碳排放影響因素的研究逐漸增多。其中，因素分解法在世界多個國家和地區的碳排放領域得到廣泛應用，是一種以比較靜態分析為理論背景的方法。其基本思想就是將目標變量在基期到報告期的變化量分解成為數個影響因素的變動組合，以此剝離出各個影響因素對于目標變量的作用方向和影響大小，進而比較得出推動或阻礙目標變量變化的驅動或抑制因素。常見的因素分解法有指數分解法（IDA）和結構分解法（SDA）。SDA的劣勢在于其對于數據的更高要求，但優勢在于基于投入產出表它可以全面分析各類直接或者間接影響因素，尤其是能夠將一個部門需求變動所帶來的間接影響反映到其他各個部門中。本文采用SDA分解法作為碳排放變動的主要分解方法。

最早將投入產出結構分解法引入能源、環境研究領域的是里昂惕夫（1970），[12]隨后許多學者紛紛效仿。結構分解模型通常有4種形式：保留交叉項；不保留交叉項，將其以不同方式分配給自變量；加權平均法以及兩級分解法。“由于不同的分解形式產生的結果存在差異，并且理論上沒有理由認為某種分解形式優于其他，可通過不同分解形式求出每個因素影響效應，然后求出其平均值，以此解釋目標變動”（Dietzenbacher和Los，1998）。[13]將投入產出模型與結構分解技術相結合的投入產出的結構分解模型（IO-SDA），因其能對經濟系統中的總量變動、結構變動等問題進行分析，所以被廣泛應用于國際貿易、經濟增長、環境保護和能源應用等領域。為了盡可能降低分解結果的誤差，本文在SDA分解法方面有所借鑒，選擇采用兩級平均分解法來對各個因素的影響效應進行定量研究。

正如引言所說，關于國際產業轉移對碳排放的影響，目前的觀點分為對立的兩類。Walter等（1979）提出“污染避難所”的假說，[2]后經過Baumol和Oates（1988）進行了完善。[14]然而Smarzynska和Wei（2001）的研究卻沒有找到可靠證據來證實污染避難所假說。[15]另一類觀點以產業轉移中存在技術“外溢效應”為由，認為產業轉移會減緩碳排放。陳楠、劉學敏、長谷部勇一（2016）對中國和日本的產業轉移中的碳排放問題進行研究，發現由于能源使用效率的提升和生產技術的改良，中國在承接了日本高碳排放水平的產業后，并沒有成為污染者天堂。[16]國內學者對區域產業轉移對碳排放影響的研究較晚一些。肖雁飛等（2014）對我國2002-2007年間區域產業轉移的碳排放轉移進行分析，發現產業轉移對碳排放的影響和地區差異性有關，在于承接地的產業選擇和產業結構在轉移中的優化水平。[17]成艾華（2013）分析了我國28個省市的碳排放強度變化隨區域產業轉移的情況，結果顯示凈轉入地區的排放強度不斷增加而碳排放凈轉出地區的強度不斷降低。[18]

在上述關于產業轉移和碳排放變化的研究中，不難發現，利用一國的單區域投入產出模型，或者雙邊投入產出模型來進行的研究，不能對產業轉移與碳排放的關系做出一般性規律的總結，來反映我國在全球視角中的產業發展和節能減排關系。本文借鑒隱含碳研究中的多區域投入產出模型，結合SDA分解法，從更廣闊的視野對國際間產業轉移所造成的國家碳排放影響進行分析。另外，本文并不聚焦隱含碳轉移及核算這一主題，而意在通過分解法測算國外拉動效應來解釋國際間經濟發展對各國碳排放的影響。

三、模型設定與數據來源

(一)模型設定

1.全球碳排放的投入產出模型

對于全球投入產出模型：首先，橫向關系上，某一國家的某一部門分別為各個國家的不同部門用于生產的中間產品和最終需求產品；縱向關系上，來自各個國家各個部門的產出投入到某一國家某一部門的總產出中。

假定全球共有I個國家，每個國家有S個部門，第i個國家第s個部門的產出是yi（s），第i個國家第s'個部門對第j個國家最終需求的貢獻為fij（s），第i個國家第s個部門對第j個國家第s’個部門的投入為zij（s，s’）。

進一步地，Zij為第i個國家向第j個國家各個部門中間投入矩陣，Fij為第i個國家向第j個國家最終需求的輸出矩陣，Yi和Vi分別為第i個國家的總產出矩陣和增加值矩陣，如下式所示：

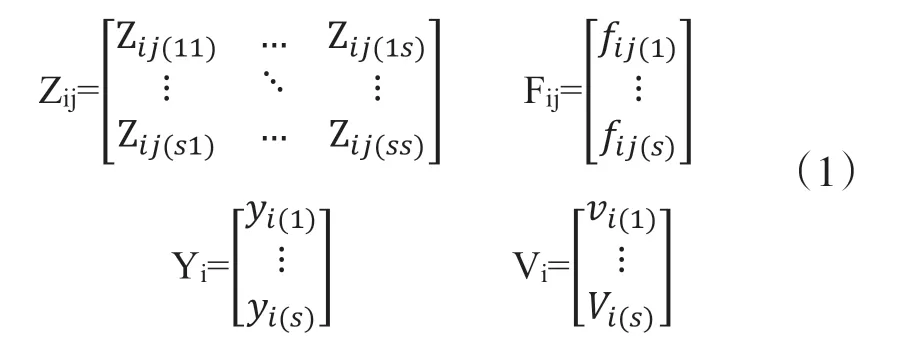
得到相應的投入產出表結構如表1所示：

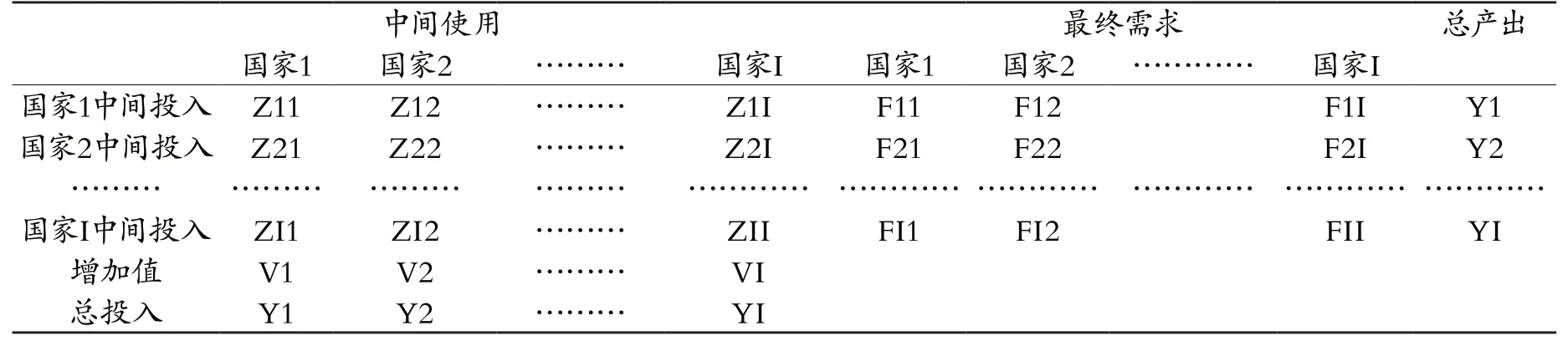
表1 世界投入產出表結構

根據表1得出，第j個國家第s’個部門產出對 第i個國家第s部門投入的直接消耗系數：

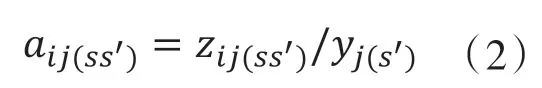
設Aij表示第j個國家的產出中，來自第i個國家的投入的直接消耗系數矩陣：

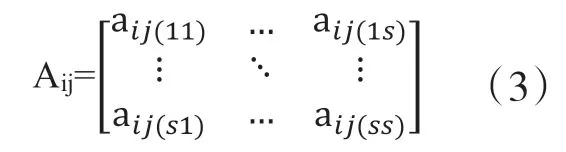
則世界投入產出模型的直接消耗系數矩陣A為

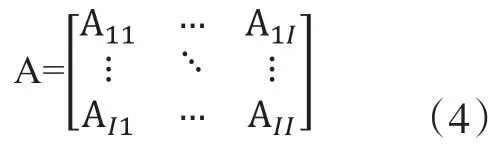
根據投入產出模型可知：

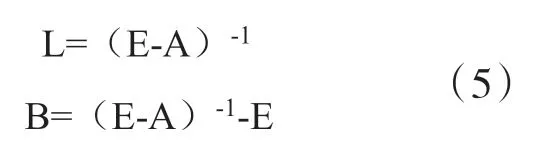
其中，L為里昂惕夫逆矩陣，B為完全消耗系數矩陣，E為SI*SI的單位矩 陣。

完全消耗系數可以在描述i部門對j部門直接投入的同時，進一步說明第i部門通過對其他部門投入而對第j部門的間接投入，這在分析各產業轉移以及伴隨其移動的碳排放時很關鍵。

由于世界各國分行業能源消耗的數據可得性問題，加之本文研究重點在于碳排放的影響因素而非核算標準，因此這里直接以各國分年份碳排放量除以當年總產值，即單位GDP碳排放強度（Carbon Intensity）來計算各國各產業的排放值。具體表示為：

其中CIi表示i國的碳排放強度，Ci表示i國該年份的碳排放總量，Yi表示i國總產出，則

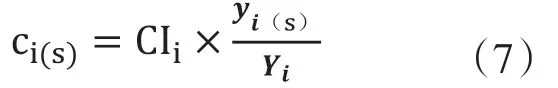
其中ci（s）為i國s產業的碳排放量，yi（s）即上文所提到的第i個國家第s個部門的產出。

將研究期間每年的投入產出表都依次處理，得到每年的碳排放投入產出表。

2.投入產出表的結構分解

結構分解法發展比較成熟，本文主要根據Miller和Blair（2009）的經典論述和框架，[19]同時參照袁志剛和饒璨2014將影響因素再按照國內外進行區分。[20]本文結構分解模型先將投入產出表中各國各行業總產出變化分解為來自最終需求影響和來自技術變化影響，其次將最終需求影響劃分為水平效應（最終需求變動影響）、混合效應（同一國家的最終需求在不同產出之間的分布變化）以及分布效應（不同國家最終需求之間的分布變化），最后再將三種不同的終需變動和技術變動都按照國內國外進行分解，最終得到國內外技術變動和終需變動對產出變化的影響。

設世界投入產出模型最終需求矩陣F和總產出矩陣Y為：

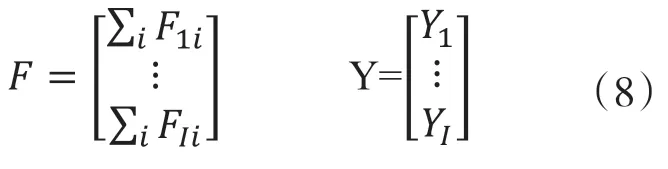
根據SDA分解模型的兩級分解辦法，將第一期的向量上標設為0，第二期的向量上標設為1，得到方程式如下：

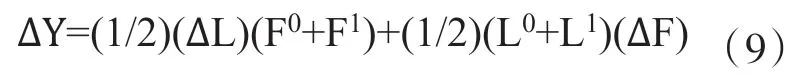
其中，△L代表技術水平變動，△F代表最終需求變動，即這兩項分別代表技術變動、總需求變化對某一行業產出變化的影響。

首先探討總需求變化對某一行業產出的影響。假設 f 為所有國家消費之和：

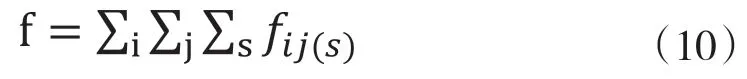
因此，每一個國家最終需求占最終需求的比重矩陣D（44*1階矩陣）為：

所有國家各個部門產出用于每一個國家最終需求的比重矩陣B（2464*44階矩陣）為：

在此基礎上，針對國內、國外的總需求變化對最終產出的影響對模型進行再分解。以中國為例，則中國與其余國家（外國）總最終需求變化量為：

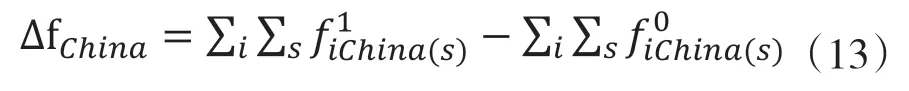
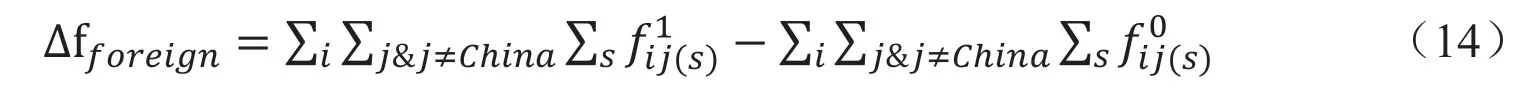
中國與其他國家最終需求占總最終需求的比重矩陣為：

所有國家各個部門產出用于中國最終與其他國家最終需求的比重矩陣為：

由以上各式可確定△F的計算方程，即國內外最終需求變化對總產出的影響:

接下來探討技術變化對行業總產出變化的影響。同樣考慮國內與國外兩方面的技術變動影響，可得：

其中△AChina、△Aforeign分別代表國內（外）技術變動的完全消耗矩陣。

對上述方程式進行整合，最終可得到制造業的結構分解式為：

即最后所有國家各行業的變動由此分解為中國技術水平的變動、國外技術水平的變動、中國最終需求變動的水平效應、國外最終需求變動的水平效應、中國最終需求變動的混合效應、國外最終需求變動的混合效應、中國最終需求變動的分布效應與國外最終需求變動的分布效應。因本文僅需要考慮國外最終需求因素，故將三種最終需求變動效應加總來進行分析。

本文選取2000—2009年這十年的投入產出表，將單位產出碳排放強度帶入該模型，除去數據不可得的臺灣地區，得到42個國家和地區各自的56個部門在九個時間段內各因素對碳排放變化量的影響。最后將計算得出的各個產業因各因素而變化的碳排放量按照國家進行加和：

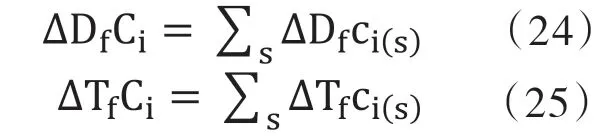
其中，△DfCi表示i國家因國外需求因素而產生的碳排放增量，△DfCi(s)表示i國家s部門因國外需求因素產生的碳排放增量；同理，△TfCi表示i國因國外技術因素而產生的碳排放增量，△TfCi(s)表示i國s部門因國外技術因素而產生的碳排放增量。

3.產業轉移的核算方法

在產業轉移方面，本文主要借鑒孫曉華（2018）所描述的產業轉移衡量方法，[21]同時參考孫植華（2018）的產業動態集聚指數。[22]為了使其適應本文模型，此處將模型略做改動，設產業轉移指數反映某一產業在一定的時間段內向某一個地區集聚的速度，能夠將產業的區域轉移方向和能力體現出來，同時能夠與之前的動態碳排放變化模型相匹配。具體公式為：

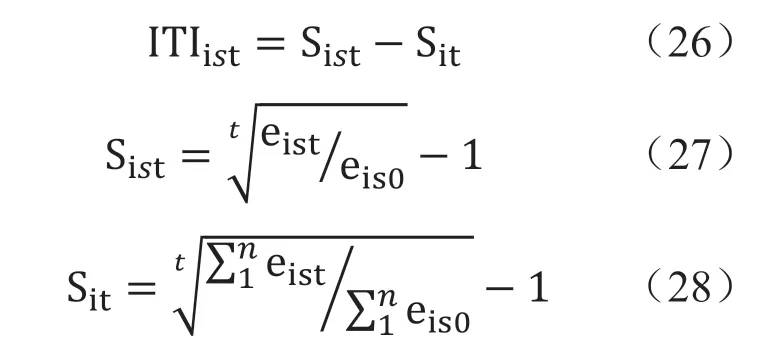
如上所示，0、t 表示時間周期，sist表示i地區中s產業的平均增速，sit表示世界范圍內j產業的平均增速，eist和eiso分別表示報告期和基期s產業在i地區的總產值，n表示世界上共有n個國家和地區。ITIist表示產業轉移系數，若數值為正，則i 地區s 產業在世界平均水平下是發展的；反之若為負，說明該產業在i 國萎縮。

最后將各個國家的部門按照該部門占國家總產出占比加權，核算出各國的產業轉移系數：

其中ITIi是i國在基期和報告期之間的產業轉移指數，ITIis表示i國s部門在基期和報告期之間的產業轉移系數。其中t 為基期到報告期經過的周期。

4.計量模型

由于本文的因變量與核心解釋變量均為基期和報告期的變化量，因此控制變量也都處理為期間內的變化值，以使模型更加合理。具體的回歸模型如公式（30）所示：

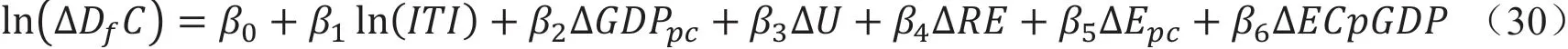
其中，△DfC是某國因國外需求因素而在核算期間內增加的碳排放量，ITI為該國這一期間內產業轉移指數。由于前者數據規模較大，進行取對數處理。而后者計算所得指數較小，采取擴大一萬倍之后取對數的模式。△GDPpc表示人均GDP變化量，△U表示城市化變化量，△RE表示可再生能源與核能變化量，△Epc表示人均耗電變化量，△ECpGDP表示單位GDP能耗變化量。

被解釋變量是國外因素所導致的本國碳排放增長。考慮到國外因素影響傳遞到國內時會隨著各國國情的不同而有所差異，因此參考已有文獻，選擇上述控制變量。

（二）數據來源

利用計量模型來研究世界各國因國外因素而增加的碳排放量與國際產業轉移之間的關系。首先選用來自WIOD數據庫的2000年—2010年①2000-2001年為時間段1，以此類推。世界投入產出表作為模型基礎②世界投入產出數據庫：http://www.wiod.org/home，加之Word Bank數據庫獲得的世界各國碳排放總量③世界銀行數據庫：https://data.worldbank.org.cn/，以計算因變量，即各國因國外因素而增加的本國碳排放量。另一方面，基于投入產出表計算得到各國產業轉移指數。首先，人均GDP可以較為客觀的反映一個國家人民的生活和消費水平，數據來源自IMF④國際貨幣基金組織數據庫：https://www.imf.org/en/Data。其次，作為一個國家，城市化程度也很大程度上影響了碳排放量。類似的，城市化水平也與碳排放有所關聯，高城市化水平可能會使得社會耗能增加，但也可能會推出一系列城市治理政策以減免碳排放。人口密度與城市化數據來源于世界銀行數據庫。除此之外，可替代能源和核能、人均耗電量以及單位GDP的能源消費也同時被考慮在內。可替代能源和核能的使用或許能對國家碳排放起到減緩作用，而電力的煤炭消費量占煤炭總消費量的比重一直很大，且在不斷上升。考慮到人均耗電量中包含許多風能等可再生能源，本文加入單位GDP能源消費的控制變量，數據來自世界銀行數據庫。⑤本文所有數據均為部門級數據，因“產業轉移”名詞所限，本文的產業皆指部門。

四、實證結果

（一）描述性統計

圖1 部分國家二氧化碳排放變化量（千噸）

如圖1所示為部分國家碳排放變化量隨時間的變化情況。限于篇幅，這里僅從發達國家與發展中國家列表中各選取幾例作為代表。發達國家二氧化碳排放量普遍呈現出下降趨勢；而發展中國家，如中國、巴西、印度、印尼等，其二氧化碳排放量卻呈現出波動態勢，增減不一。

由第二部分描述的模型可得九個區段內42國家56 個部門的國外需求拉動碳排放量與部門產業轉移指數的關系，如圖2所示：

表2表示變量的描述性統計。

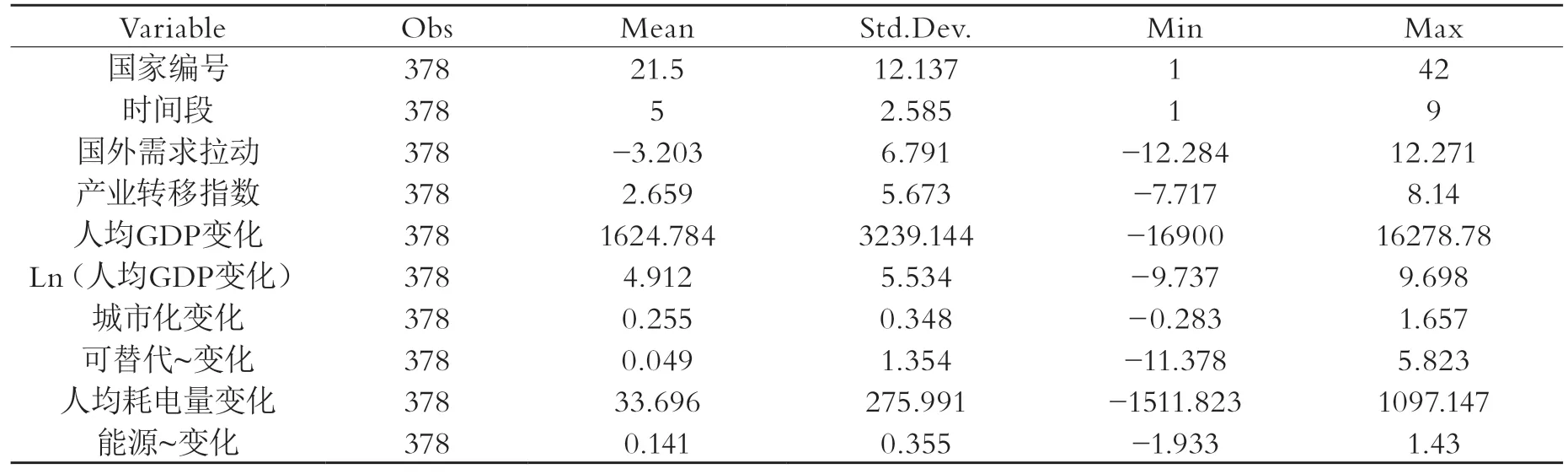
表2 描述性統計

（二）回歸結果

通過Hausman檢驗和LM檢驗，結果顯示混合效應優于隨機效應和固定效應。借助Stata軟件得到回歸結果如表3所示。

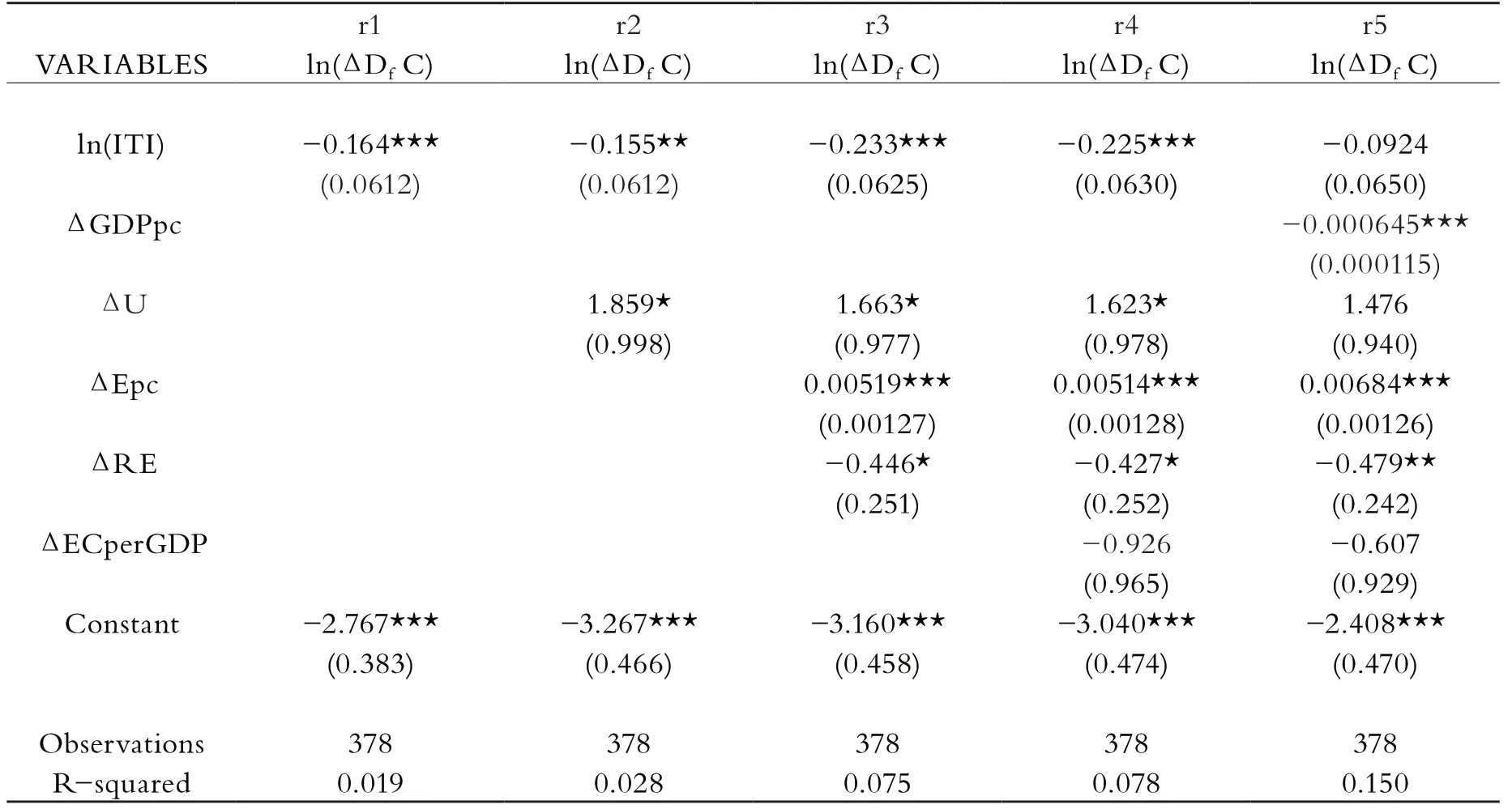
表3 混合效應回歸模型結果

回歸結果通過了VIF共線性檢驗，計量回歸模型有效。根據表3的實證結果，除去最后一列回歸，主要研究變量基本是顯著的。

在第一列回歸結果中，主要研究變量l n（ITI）在1%的水平上顯著為負，然而系數的符號和本文預期情況相反。即隨著產業的遷入，國外需求對本國的碳排放量有抑制作用。在第二列回歸結果中，新加入的城市化變化率在10%的水平上顯著為正。逐次加入其他變量，通過第三、四列回歸結果發現，單位GDP能耗并不顯著，因此剔除。第三列是結果比較理想的回歸結果。結果顯示，城市化和人均耗電量的變化與外需拉動的碳排放變化呈正相關關系。或許是因為城市化和人均耗電量從一定程度上反映了一個國家能源使用的水平和效率，因此當國外需求增加時，一個國家的能源使用和污染情況通過國內產出增加而體現出來。另一方面，可再生能源與核能在10%的水平上顯著為負，即這一指標和產業遷移指數對碳排放都有抑制作用。顯然，可再生能源和核能的使用對于環境污染有著很好的抑制作用。然而，主要研究變量的系數為負，這與本文的預期結果并不相符。

針對這一問題，本文有如下猜測：①由于樣本中，發達國家和發展中國家并未區分，而發達國家可能會有選擇的遷入具有發展前景的低污染產業，因此對回歸造成了影響。②相對于用SDA分解法將國內因素剔除的因變量，產業轉移指數卻并未將國內因素排除在外。國內本身的產業轉移和壯大將會一定程度上影響回歸結果。本文會在接下來的穩健性檢驗中進一步探討這一問題。

五、穩健性檢驗

（一）將國外技術變化納入模型

在第二節提到的結構分解模型中，將引起本國碳排放增加的國外因素分成了技術和需求兩個部分。在前一節的計量模型中，將技術因素剝離了出去，得到了“產業遷移對國內碳排放有抑制效果”這一結論。為了測試其穩健性，進一步探索國外因素的影響，這里對技術因素和國外所有因素，即需求和技術的加總，分別進行計量回歸。

首先將因變量設置為國外技術需求引起的碳排放增加（lnΔT_fC），將控制變量依次加入模型，其回歸結果如下：

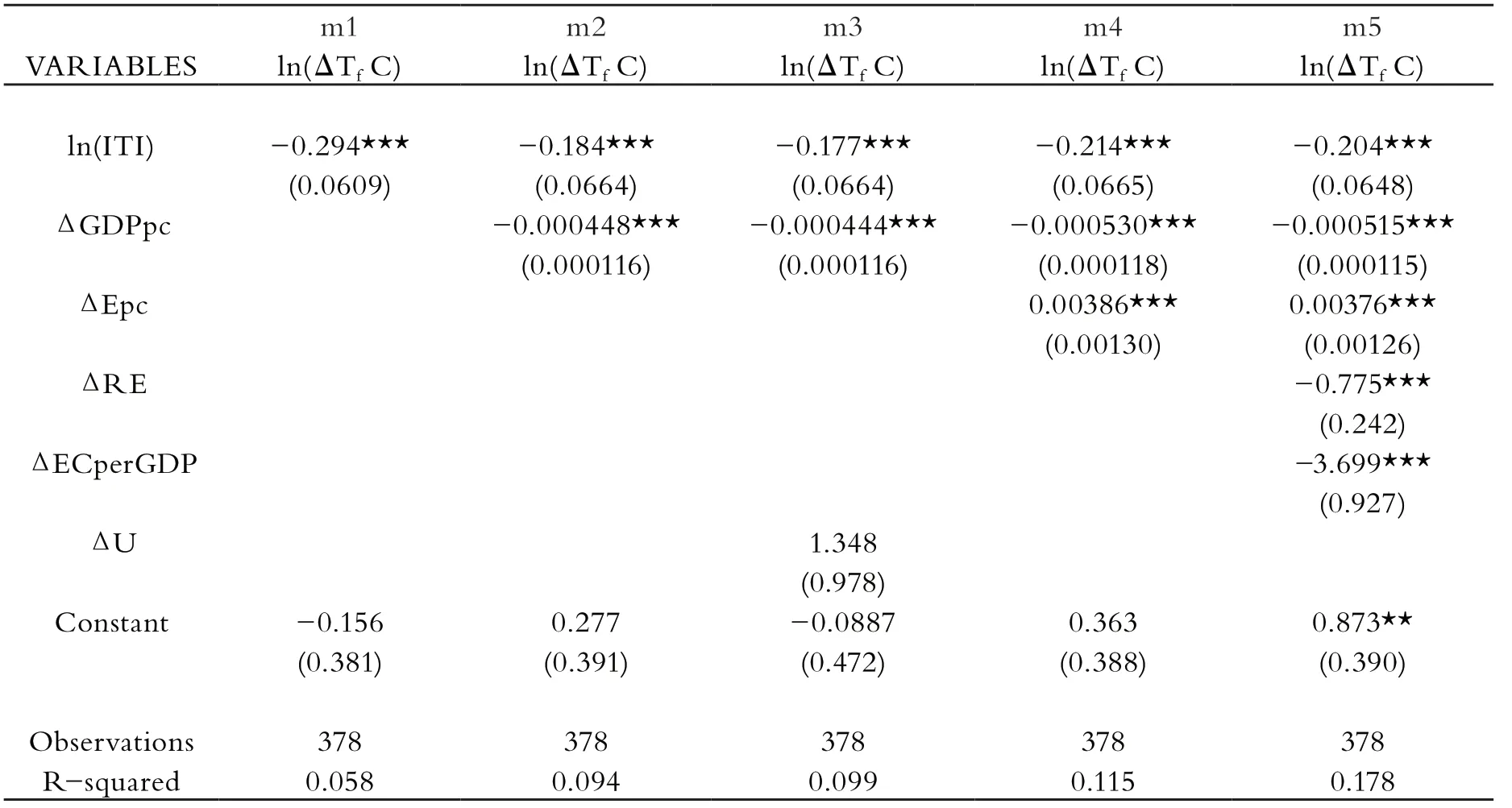
表4 第一次穩健性檢驗（1）

回歸結果表明：在第二列中，城市化變化量這一控制變量并不顯著，因而在后面的回歸中剔除。主要研究變量即ln（ITI）在所有回歸中都十分顯著，且系數均為負。因而可以確定，國外技術的轉入確實會對本國碳排放產生顯著的抑制效果。技術溢出效應在這一模型下是成立的。控制變量中，人均GDP變化量，可再生能源變化量以及單位GDP能源強度的系數都為負。人均GDP的增長代表著國民生活水平以及國內能源使用率的提升，同時更好的生活有利于培養國民的低碳意識，因而其增長對碳排放有抑制作用。另一方面，人均耗電量的提升確實促進了本國碳排放量的增長。

將因變量替換為所有國外因素導致的碳排放變化量：

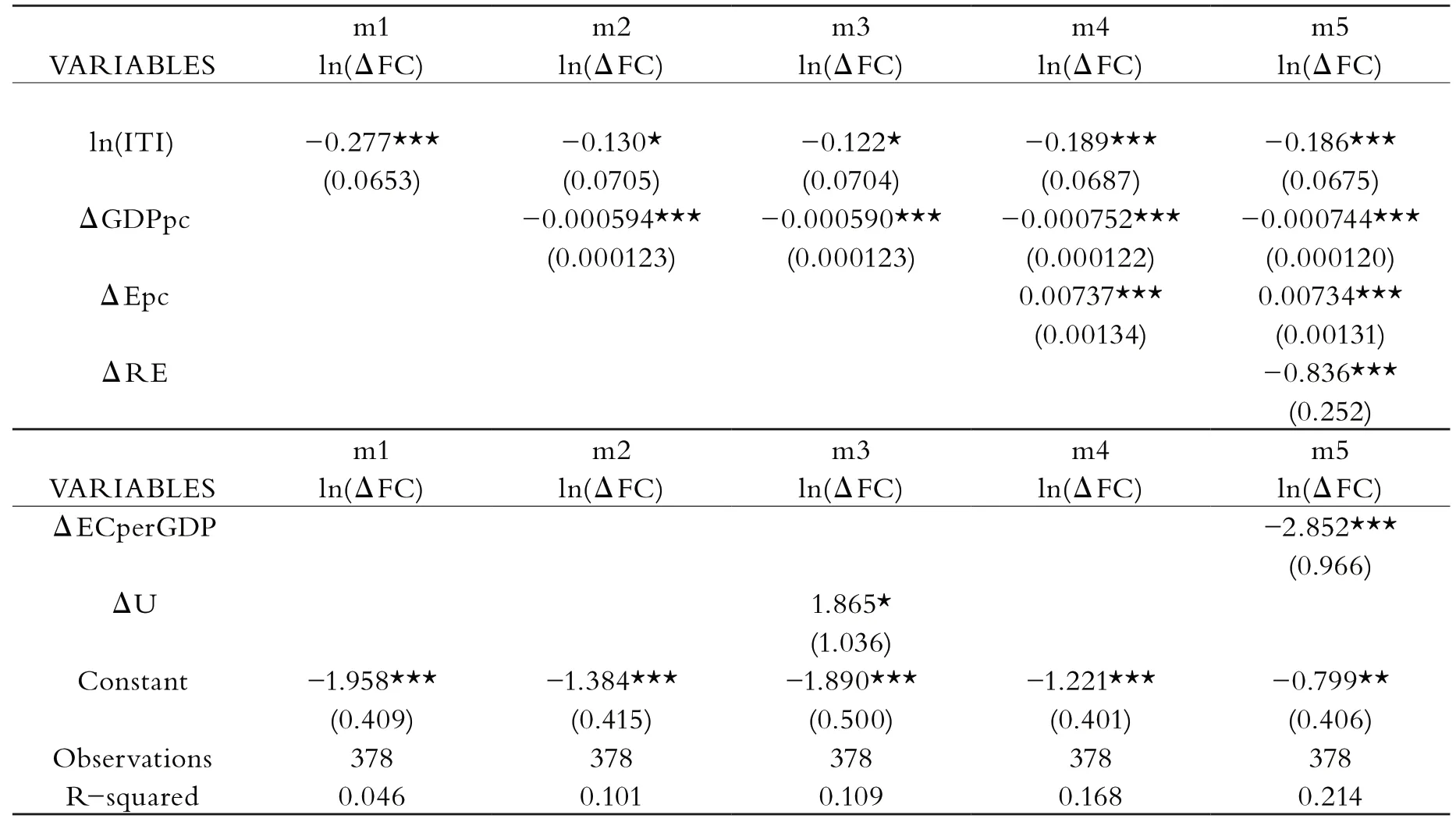
表5 第一次穩健性檢驗（2）

可以看到各變量回歸結果依舊顯著。相比較表一中的基本回歸結果，產業轉移對碳排放的影響程度有所降低；R square有所提高，說明加入技術水平的模型對現實的擬合程度更高。經過上述檢驗，“產業遷移對國內碳排放有抑制效果”這一結論更加穩健，說明兩者之間確實存在緊密聯系。然而其影響方向與預計情況相反的問題依舊沒有得到解釋。

（二）區分各國的發展程度

由于樣本中的各個國家和地區發展水平有極大差異，接下來按照國際標準將發達國家區分開來，分別進行回歸。該區分標準綜合了HDI VH聯合國開發計劃署人類發展指數極高的國家；WB HIE世界銀行高收入經濟體；IMF AE國際貨幣基金組織發達經濟體；CIA AE中央情報局《世界概況》發達經濟體等。

發達國家和發展中國家回歸結果分別如表6、7所示。首先，將上述兩表與原回歸結果相比較，不論是發達國家還是發展中國家，回歸結果中各個系數的符號都沒有改變。對于發達國家而言，產業轉移和可再生能源使用這兩個變量對碳排放的影響更大一些，而城市化對碳排放的影響不再顯著。較之發達國家，發展中國家國外因素對本國碳排放增量的影響幅度在本文的模型量綱下多出了30%左右。對于發展中國家而言，產業遷移對碳排放的影響也有一定增加，同時城市化和人均耗電量這兩個因素的系數顯著增加。顯然，對于發展中國家而言，城市化和耗電量的發展會更多的影響到碳排放。另外，可再生能源的使用這一因素不再顯著，很可能是這類能源在發展中國家的使用非常有限而導致的。

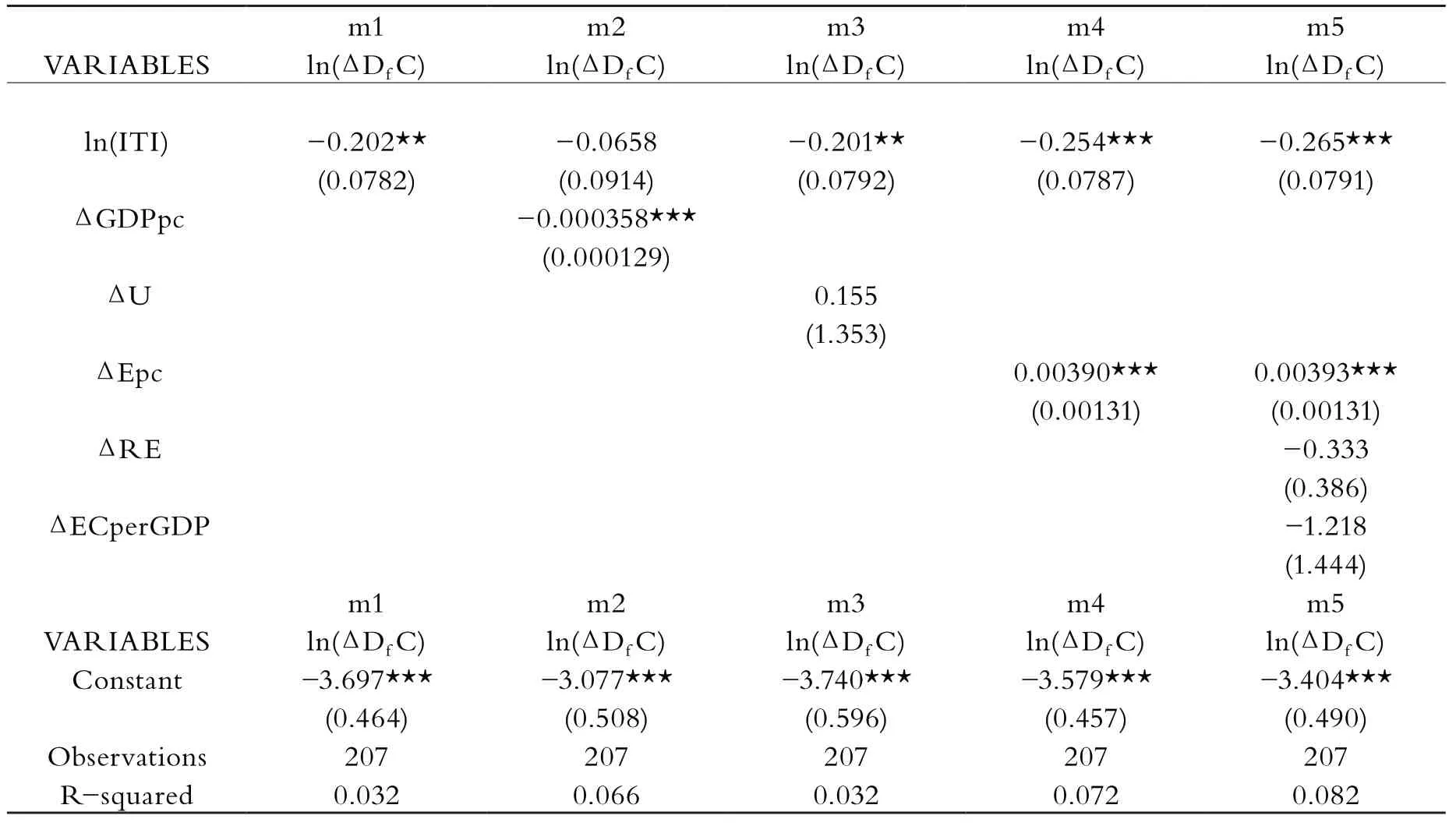
表6 第二次穩健性檢驗（發達國家）

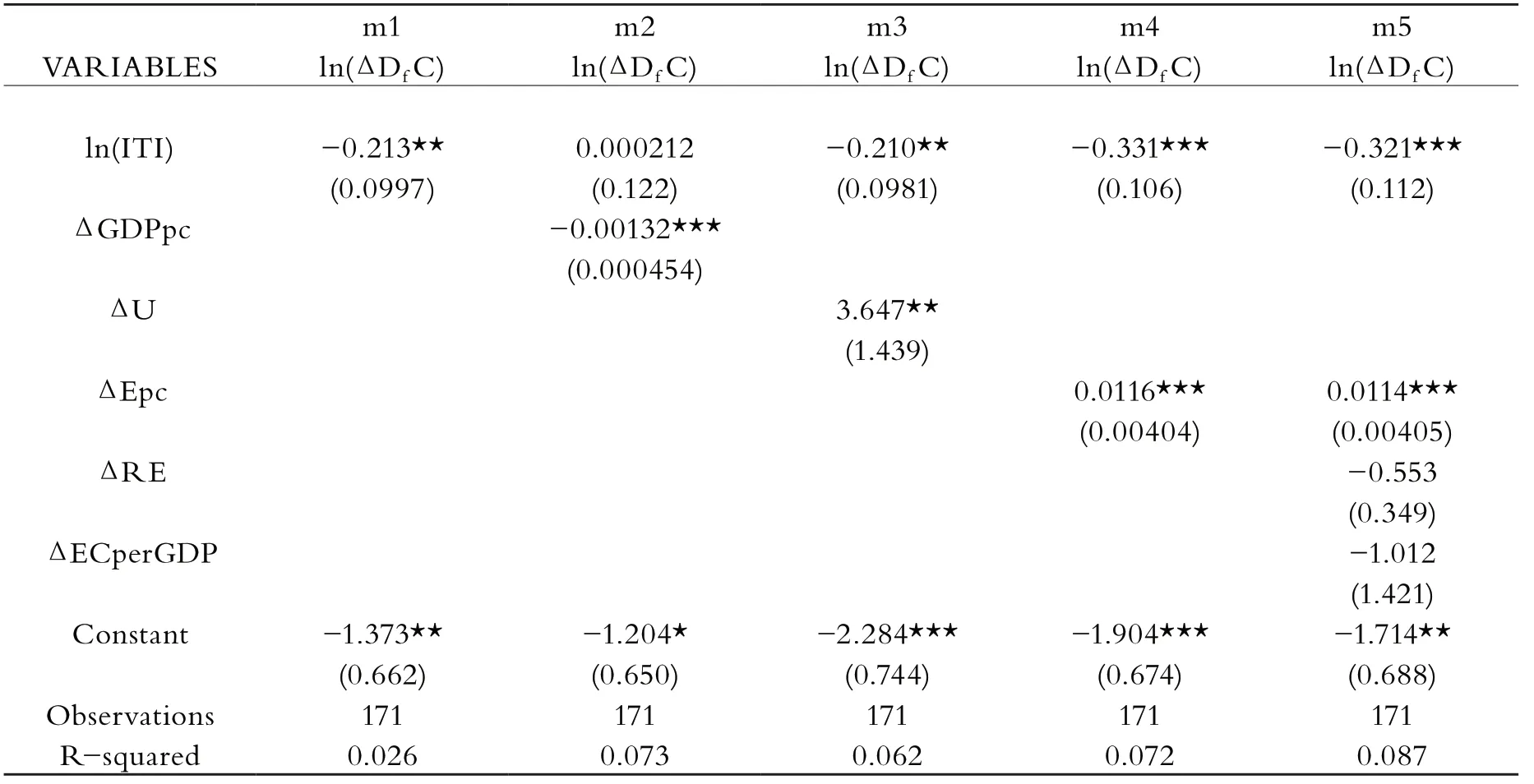
表7 第二次穩健性檢驗（發展中國家）

（三）對產業轉移指數的進一步細化

在原模型中，產業轉移指數的計算借鑒了孫曉華（2018）中的研究方法。然而相對于用SDA分解法將國內因素剔除的因變量，產業轉移指數卻并未將國內因素排除在外。在一個特定國家，尤其是發展中國家，國內某一產業若能發展壯大并融入世界經濟體系，則其自身比較優勢以及資金、政策的傾斜等都會提供非常可觀的貢獻。而隨著該國技術水平的發展，在發展產業的同時逐漸控制該產業的污染情況也就變得順理成章。為了排除這一干擾，下面對該變量的模型進行調整。

考慮到投入產出表中各個國家之間的緊密聯系，這里采用完全消耗系數矩陣來進行處理。將完全消耗系數矩陣按照各產業產值加權，而后將對角線上本國的中間品投入矩陣替換為0矩陣，即Zii=Zero。

將該產業所有來自國外的中間品投入加總，作為，則：

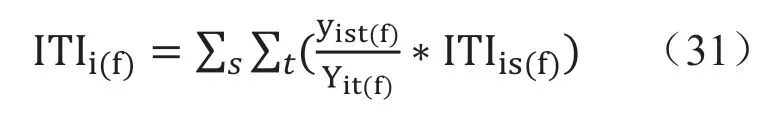
其中，角標f表示與國外產品轉移有關，因而ITIi（f）表示i 國在基期和報告期之間的國外產業轉移指數。

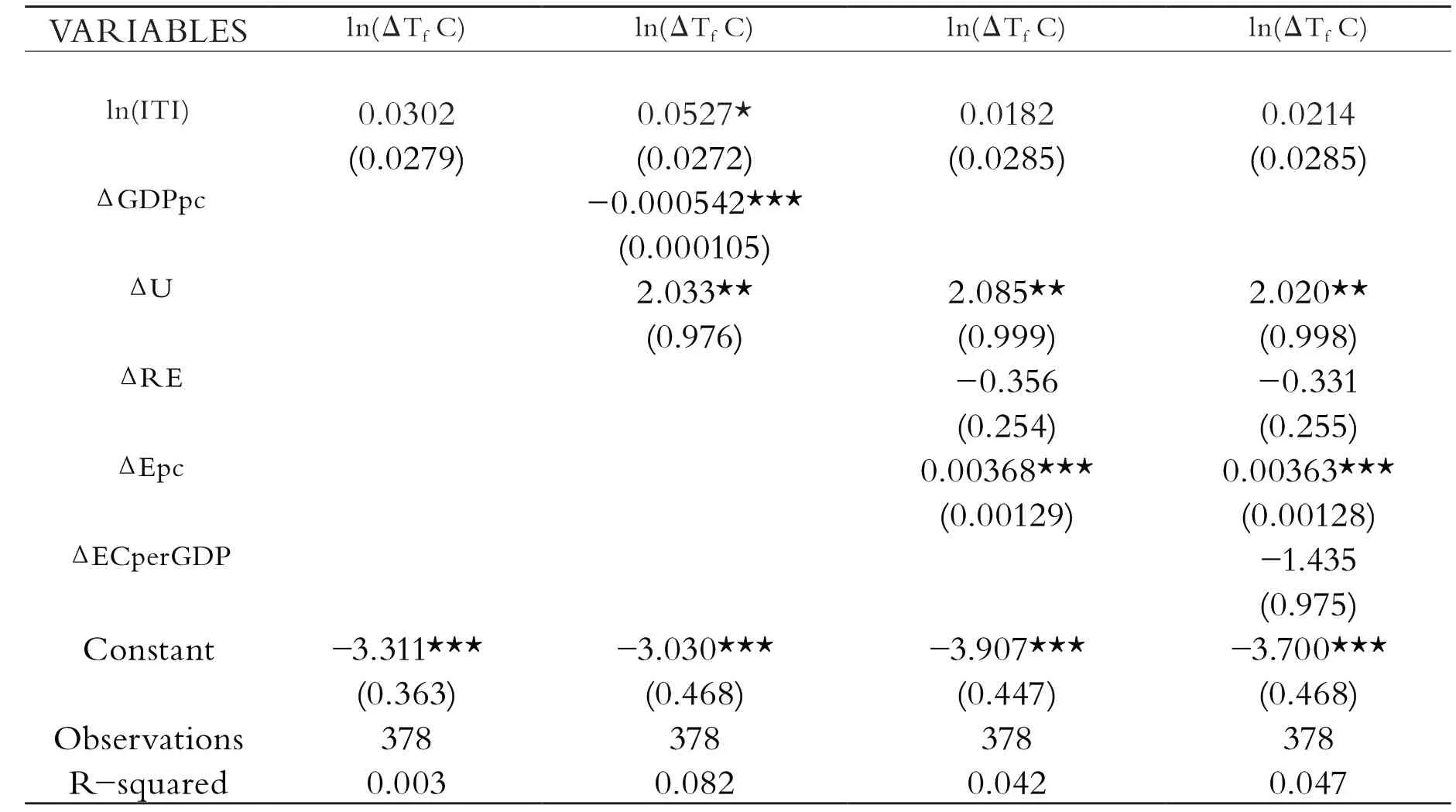
表8 第三次穩健性檢驗

將計算得出的國外產業轉移指數代替原指數進行計量回歸。因變量為國外需求拉動的碳排放變化量，結果如上表8所示。結果顯示：雖然國外產業轉移指數的系數轉變為正值，然而其在多次回歸中都不顯著。這說明，當國內產業轉移按照上述模型剔除后，國外需求對國內碳排放的影響并不顯著。另外，城市化和人均耗電量則對碳排放有顯著的正向影響。

六、結語

本文旨在探索國際間產業轉移對本國由國外因素引起碳排放變化量的影響，選取世界各國2000-2009年相關數據，將多區域投入產出模型和結構分解法相結合，以動態視角計算九個時段內各國數據的變化情況，并通過計量模型進行回歸分析。通過實證研究，本文得到以下結論：一是國際間產業轉移確實會對產業接收國中由國外因素拉動的碳排放產生顯著影響。當國內產業發展和轉移因素被納入考慮時，國際間產業轉移會對各國由國外需求因素而導致的碳排放增量產生抑制作用，這一結論對“污染避難所”這一理論進行了駁斥；二是產業轉移在發達國家對碳排放的影響并沒有在發展中國家那樣凸顯。在本文的模型計算下，在發展中國家國外因素對碳排放量的影響程度要比在發達國家高出約30%；三是在國際間產業轉移所帶來的影響中，國外技術因素對碳排放增量的抑制作用比之需求因素更為顯著，印證了“技術溢出效應”的存在。

有選擇的引入國外產業，對有效減少國內碳排放有積極作用。同時，作為發展中國家，我國碳排放量對國際產業轉移較為敏感，因此，對國際產業轉移應持謹慎態度，鼓勵高技術、低能耗的產業引進，將會有利于控制我國的環境污染狀況、遏制碳排放增勢。