基于頻率偏移面積的功率缺額計(jì)算及低頻減載整定
劉克天 張 鈞 李 軍 陳 凡
(1. 南京工程學(xué)院電力工程學(xué)院 南京 211167 2. 國(guó)網(wǎng)能源研究院有限公司電網(wǎng)發(fā)展綜合研究所 北京 102209)
0 引言
特高壓及可再生能源發(fā)電系統(tǒng)容量的不斷增大,導(dǎo)致電力系統(tǒng)轉(zhuǎn)動(dòng)慣量持續(xù)下降,系統(tǒng)調(diào)頻困難且故障情況下所遭受的功率缺額也越來(lái)越大,頻率穩(wěn)定問題日益突出[1-2]。當(dāng)前,系統(tǒng)調(diào)頻仍主要由傳統(tǒng)機(jī)組完成,隨著儲(chǔ)能技術(shù)的發(fā)展,儲(chǔ)能也逐漸參與系統(tǒng)調(diào)頻,改善系統(tǒng)的頻率穩(wěn)定性[3-4]。頻率穩(wěn)定控制措施主要為第二道防線的自動(dòng)切負(fù)荷及第三道防線的低頻減載,兩者各有優(yōu)缺點(diǎn),均有廣泛的應(yīng)用。
作為最后一道防線的低頻減載在防止頻率崩潰方面有著不可替代的作用。低頻減載整定方法主要有傳統(tǒng)法、半適應(yīng)法和自適應(yīng)法[5]。傳統(tǒng)法以系統(tǒng)可能出現(xiàn)的最大功率缺額事件確定切負(fù)荷總量,采用“逐次逼近”確定低頻減載的動(dòng)作輪次及各輪次切負(fù)荷量[6]。半適應(yīng)法和自適應(yīng)法采用初始頻率下降率計(jì)算系統(tǒng)的功率缺額并進(jìn)行低頻減載整定。兩者區(qū)別在于半適應(yīng)法只有首輪切負(fù)荷量根據(jù)功率缺額計(jì)算結(jié)果整定,自適應(yīng)法則是將所計(jì)算的功率缺額在所有輪次之間進(jìn)行分配[7]。
低頻減載整定的核心內(nèi)容為切負(fù)荷總量的確定,即系統(tǒng)功率缺額的計(jì)算。功率缺額計(jì)算主要有單機(jī)等值模型法、時(shí)域仿真法以及基于廣域量測(cè)數(shù)據(jù)的多機(jī)模型法。基于單機(jī)等值模型,文獻(xiàn)[8]考慮旋轉(zhuǎn)備用、負(fù)荷頻率效應(yīng)及水輪機(jī)調(diào)速系統(tǒng)進(jìn)行低頻減載方案整定和優(yōu)化,減小了切負(fù)荷總量。基于多機(jī)系統(tǒng)的時(shí)域仿真結(jié)果,文獻(xiàn)[9]建立系統(tǒng)動(dòng)態(tài)頻率與發(fā)電機(jī)出力增量、負(fù)荷增量之間的關(guān)系,獲得系統(tǒng)的頻率調(diào)節(jié)系數(shù),計(jì)算功率缺額,進(jìn)行低頻減載整定。文獻(xiàn)[10]使用慣性中心頻率計(jì)算系統(tǒng)的功率缺額,提出一種計(jì)及電壓穩(wěn)定的自適應(yīng)協(xié)調(diào)低頻減載策略。文獻(xiàn)[11]定義了頻率暫態(tài)穩(wěn)定指標(biāo),建立了單機(jī)系統(tǒng)頻率響應(yīng)的解析模型。基于廣域量測(cè)數(shù)據(jù),文獻(xiàn)[12-13]使用線性化的方法建立多機(jī)系統(tǒng)動(dòng)態(tài)頻率與功率缺額之間的關(guān)系。文獻(xiàn)[14]對(duì)復(fù)雜電網(wǎng)頻率動(dòng)態(tài)特性進(jìn)行分析,建立了基于廣域量測(cè)局部信息的系統(tǒng)功率缺額估計(jì)模型。文獻(xiàn)[15]以總切負(fù)荷量最小為目標(biāo),提出受端電網(wǎng)分層優(yōu)化切負(fù)荷策略。基于人工智能算法,文獻(xiàn)[16]使用v-SVR支持向量機(jī)和機(jī)器學(xué)習(xí)方法快速計(jì)算擾動(dòng)后系統(tǒng)頻率動(dòng)態(tài)特性。文獻(xiàn)[17]在進(jìn)行低頻減載整定時(shí),直接控制用戶側(cè)智能家居電器等用戶側(cè)的可控負(fù)荷,有效降低了切負(fù)荷量。
電力系統(tǒng)頻率具有時(shí)空分布特性[18]。因此,擾動(dòng)后系統(tǒng)各母線頻率并不完全相同,僅使用擾動(dòng)后瞬間各母線頻率斜率并不能準(zhǔn)確計(jì)算系統(tǒng)的功率缺額。發(fā)生功率缺額后,各母線頻率由正常值下降到低頻減載首輪動(dòng)作值的時(shí)間約為零點(diǎn)幾秒至幾秒。因此,本文對(duì)低頻減載首輪動(dòng)作前各母線頻率曲線所蘊(yùn)含的系統(tǒng)信息進(jìn)行挖掘,使用各母線頻率偏移面積計(jì)算系統(tǒng)功率缺額;然后,根據(jù)功率缺額的大小,設(shè)計(jì)不同的低頻減載方案,使低頻減載方案更具有針對(duì)性和有效性。
1 基本假設(shè)及功率缺額計(jì)算思路
慣性中心(Center of Inertia, COI)頻率反映了電力系統(tǒng)作為整體在遭受擾動(dòng)后所呈現(xiàn)的動(dòng)態(tài)行為,廣泛應(yīng)用于電力系統(tǒng)頻率動(dòng)態(tài)分析與低頻減載整定等方面。圖1和圖2分別為IEEE 9母線系統(tǒng)及IEEE 145母線系統(tǒng)發(fā)生功率缺額事件后母線頻率及系統(tǒng)慣性中心頻率。
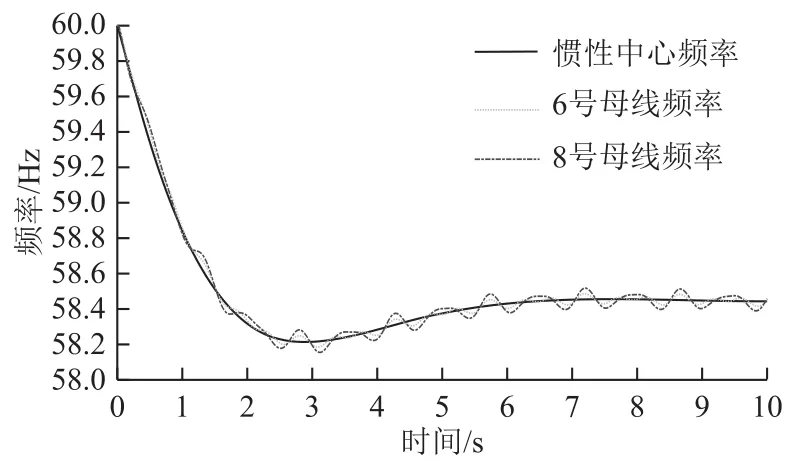
圖1 IEEE 9系統(tǒng)負(fù)荷母線及系統(tǒng)慣性中心頻率Fig.1 Different frequencies of IEEE 9 system
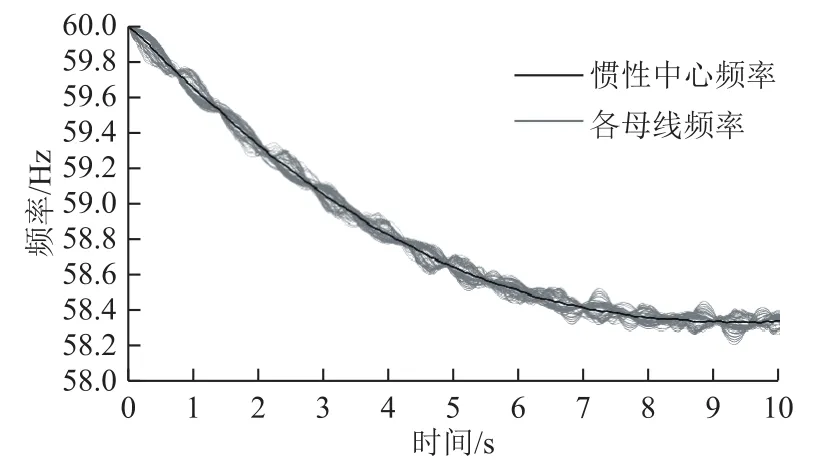
圖2 IEEE 145系統(tǒng)負(fù)荷母線及系統(tǒng)慣性中心頻率Fig.2 Different frequencies of IEEE 145 system
由圖1和圖2可以看出:發(fā)生功率缺額事件后,兩個(gè)系統(tǒng)沒都有發(fā)生暫態(tài)失穩(wěn),且各發(fā)電機(jī)保持同步,系統(tǒng)中各母線頻率圍繞慣性中心頻率上下波動(dòng)。進(jìn)一步地,圖3a分別畫出圖1中0~1s內(nèi)母線頻率與慣性中心頻率,由于各母線頻率圍繞慣性中心頻率上下波動(dòng),因此各頻率曲線與額定頻率在一相同時(shí)刻ts所圍成的面積近似相等。A、B、C分別為系統(tǒng)慣性中心頻率及各負(fù)荷母線頻率與時(shí)間軸ts的交點(diǎn),O、P為額定頻率與時(shí)間軸0、ts的交點(diǎn)。
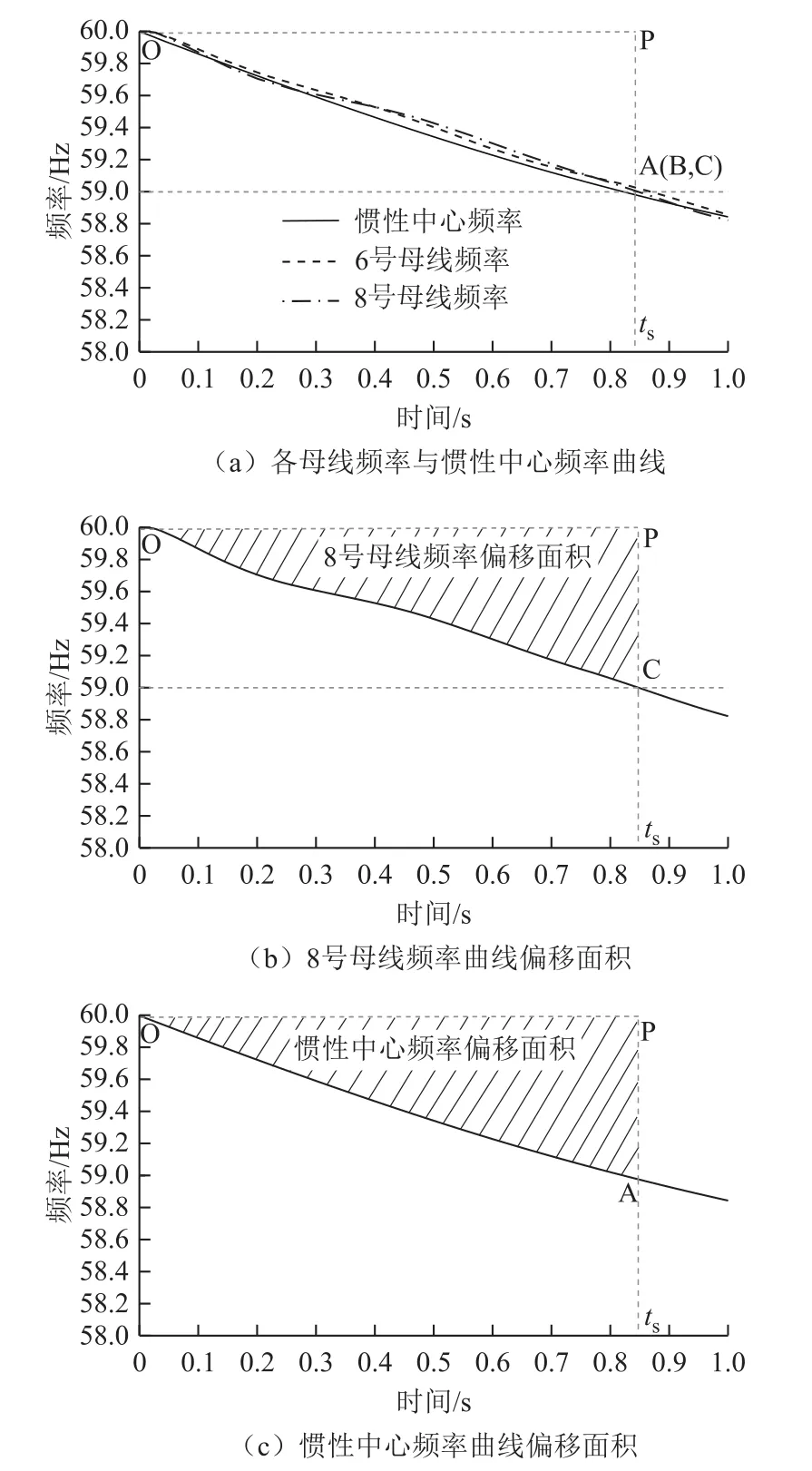
圖3 慣性中心及母線頻率曲線偏移面積Fig.3 Deviation area of COI and bus frequencies
進(jìn)一步地,忽略負(fù)荷、網(wǎng)損的變化及調(diào)速器的作用,當(dāng)系統(tǒng)發(fā)生功率缺額事件時(shí),系統(tǒng)慣性中心頻率將以恒定速度下降,當(dāng)系統(tǒng)功率缺額分別為Pd1、Pd2時(shí),系統(tǒng)慣性中心頻率如圖4所示。
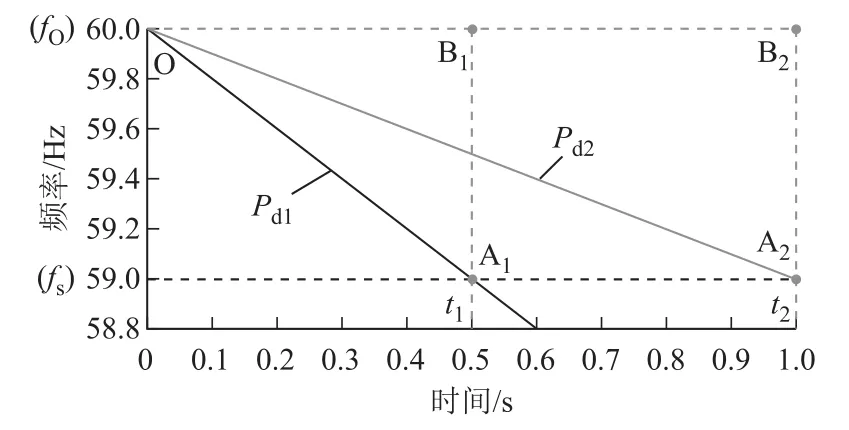
圖4 不同功率缺額情況下系統(tǒng)慣性中心頻率Fig.4 COI frequencies with different power deficits
圖4中,fO、fs分別為系統(tǒng)的額定頻率和低頻減載首輪工作頻率;t1、t2為功率缺額分別為Pd1、Pd2時(shí)慣性中心頻率達(dá)到低頻減載首輪動(dòng)作頻率的時(shí)刻。
Pd1、Pd2所對(duì)應(yīng)的慣性中心頻率偏移面積分別為三角形OA1B1、OA2B2的面積,其表達(dá)式為
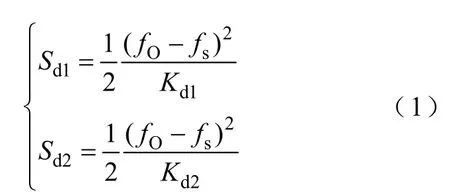
式中,Sd1、Sd2分別為Pd1、Pd2所對(duì)應(yīng)的慣性中心頻率偏移面積;Kd1、Kd2分別為Pd1、Pd2所對(duì)應(yīng)的慣性中心頻率下降速度。
由式(1)可以看出,低頻減載首輪動(dòng)作頻率確定后,慣性中心頻率偏移面積與其下降速度成反比,而慣性中心頻率下降速度與系統(tǒng)功率缺額成正比。因此,慣性中心頻率偏移面積與功率缺額成反比。所以,系統(tǒng)慣性中心頻率偏移面積能夠在一定程度上反映系統(tǒng)功率缺額的情況。
基本假設(shè):功率缺額后,如果系統(tǒng)沒有發(fā)生暫態(tài)失穩(wěn),且各發(fā)電機(jī)保持同步,則各母線頻率圍繞著系統(tǒng)慣性中心頻率上下波動(dòng),各母線頻率與慣性中心頻率曲線在同一時(shí)刻與額定頻率所圍面積近似相等,即圖3b中8號(hào)母線頻率偏移面積(OCPO所圍陰影部分)與圖 3c中慣性中心頻率偏移面積(OAPO所圍陰影部分)近似相等。
系統(tǒng)功率缺額計(jì)算思路:發(fā)生功率缺額后,系統(tǒng)各母線頻率與系統(tǒng)慣性中心頻率同一時(shí)刻的頻率偏移面積近似相等。因此,安裝在各母線的低頻減載通過(guò)測(cè)量本地頻率到達(dá)某一時(shí)刻的偏移面積,便可確定系統(tǒng)慣性中心頻率在該相同時(shí)刻的偏移面積。如果假設(shè)低頻減載首輪動(dòng)作頻率為59Hz,則以8號(hào)母線達(dá)到低頻減載首輪動(dòng)作頻率59Hz的時(shí)刻ts為例,通過(guò)測(cè)量圖3b中8號(hào)母線頻率偏移面積,便可確定圖3c中系統(tǒng)慣性中心頻率在時(shí)刻ts的偏移面積。于是,如果能夠確定系統(tǒng)慣性中心頻率ts時(shí)刻偏移面積與系統(tǒng)功率缺額之間的關(guān)系,各低頻減載裝置便可通過(guò)測(cè)量其母線頻率偏移面積來(lái)計(jì)算系統(tǒng)的功率缺額,進(jìn)而進(jìn)行低頻減載的整定。
2 基于頻率偏移面積的功率缺額計(jì)算
2.1 基本假設(shè)的理論證明
系統(tǒng)中各發(fā)電機(jī)轉(zhuǎn)子運(yùn)動(dòng)方程[19]為
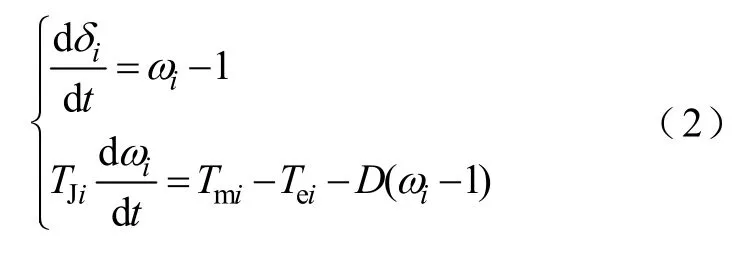
式中,δi為發(fā)電機(jī)i的功角;ωi為發(fā)電機(jī)i的角速度標(biāo)幺值;TJi為發(fā)電機(jī)i的慣量;Tmi、Tei分別為發(fā)電機(jī)轉(zhuǎn)子的機(jī)械轉(zhuǎn)矩和電磁轉(zhuǎn)矩;D為發(fā)電機(jī)轉(zhuǎn)子的機(jī)械阻尼系數(shù)。
忽略D,時(shí)間基準(zhǔn)取1s,式(2)可表示為
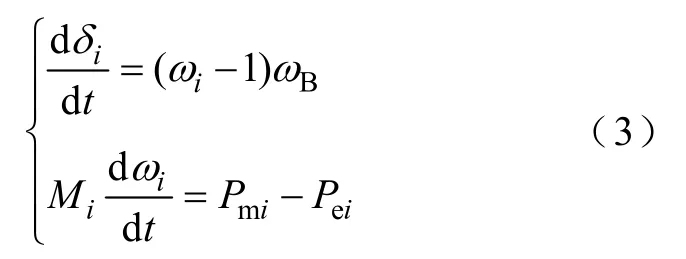
式中,Mi、Pmi、PeGi分別為發(fā)電機(jī)i的慣性時(shí)間常數(shù)、轉(zhuǎn)子的機(jī)械功率和電磁功率。
進(jìn)一步得到發(fā)電機(jī)功角及角速度偏移值為
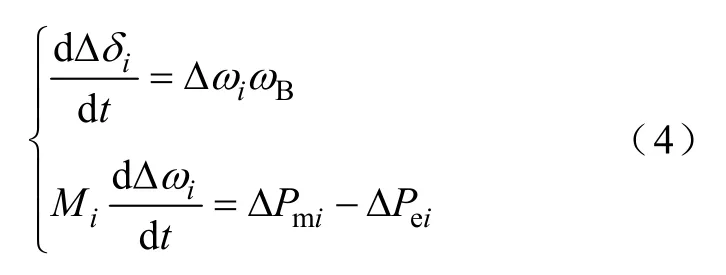
系統(tǒng)中發(fā)電機(jī)數(shù)量為m,忽略網(wǎng)耗及發(fā)電機(jī)內(nèi)阻抗,對(duì)網(wǎng)絡(luò)方程進(jìn)行線性化,則發(fā)電機(jī)電磁功率偏移值可表示[12]為

式中,ΔPe=[ΔPe1… ΔPem]T;Δδ=[Δδ1… Δδm]T;H與潮流計(jì)算中雅克比矩陣具有相同的表達(dá)形式。
假設(shè)發(fā)電機(jī)機(jī)械功率不變,將式(5)代入式(4),得到m臺(tái)發(fā)電機(jī)轉(zhuǎn)子運(yùn)動(dòng)的狀態(tài)方程為
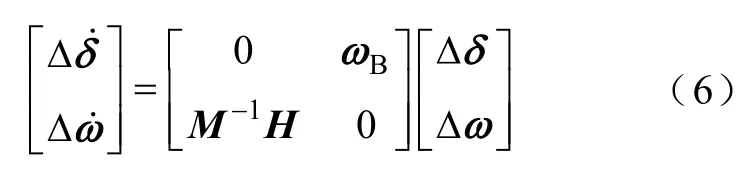
式中,M=diag(M1,…,Mm);Bω=diag(ωB,…,ωB)。
在t=0時(shí)刻,發(fā)電機(jī)母線i負(fù)荷突然增加Pdi,則式(6)可表示為
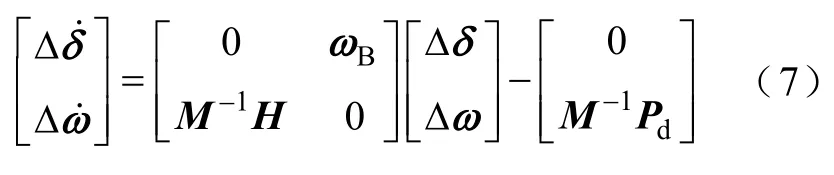
式中,Pd=[Pd1…Pdi…Pdm]T。
Δδ與 Δω初始值為 0,對(duì)式(7)進(jìn)行拉氏變換,得到角速度偏移值為
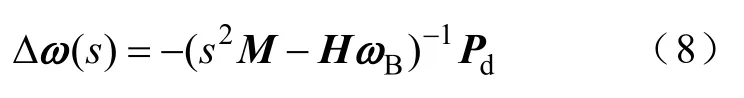
以兩機(jī)系統(tǒng)為例,t=0時(shí)刻在發(fā)電機(jī)母線 2處突然增加負(fù)荷Pd2,發(fā)電機(jī)角速度偏移值為
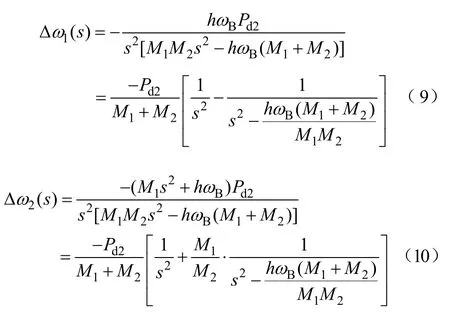
其中,h為矩陣H中的元素,其表達(dá)式為
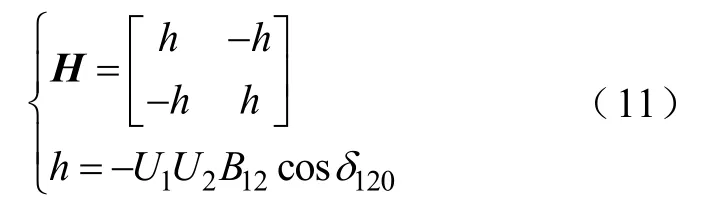
式中,U1、U2分別為發(fā)電機(jī) 1、2機(jī)端電壓,由于忽略了發(fā)電機(jī)內(nèi)部阻抗,也為發(fā)電機(jī)電動(dòng)勢(shì);B12為發(fā)電機(jī)1、2之間互導(dǎo)納的虛部;δ120為t=0時(shí)刻發(fā)電機(jī)1、2之間的功角差。
系統(tǒng)慣性中心角速度偏移值為
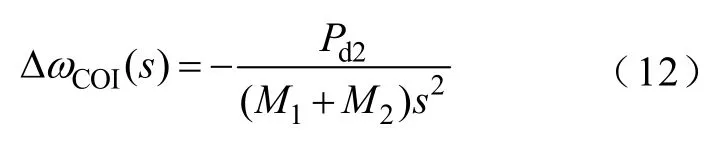
式中,M1、M2分別為發(fā)電機(jī)1、2慣性常量。
由于發(fā)電機(jī)1、2沒有發(fā)生暫態(tài)失穩(wěn),仍保持同步,則δ120的絕對(duì)值小于90°。在式(11)中,由于B12>0,cosδ120>0,則h<0,因此式(9)、式(10)、式(12)所對(duì)應(yīng)的發(fā)電機(jī)1、2及慣性中心角速度偏移值的時(shí)域表達(dá)式分別為
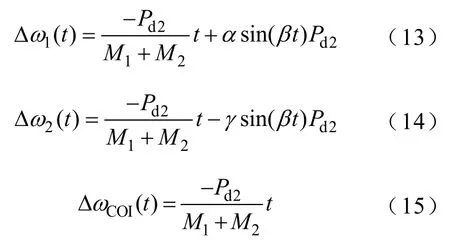
式中,α、β、γ分別為
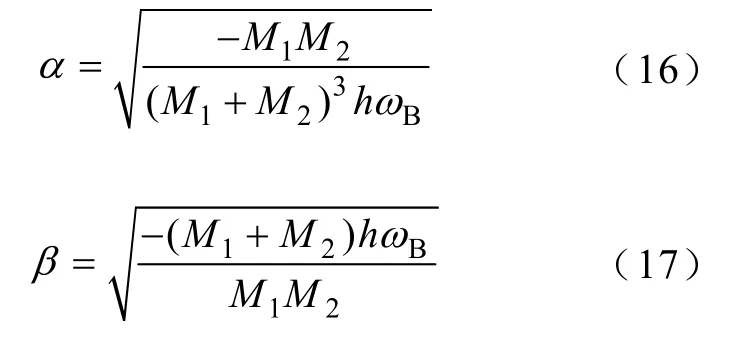
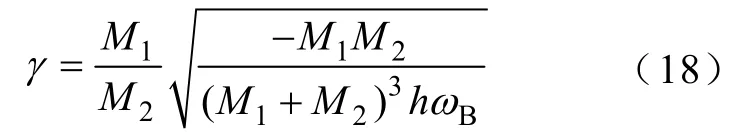
由式(13)~式(15)可以看出:發(fā)電機(jī)2機(jī)端負(fù)荷突然增加后,各角速度圍繞著慣性中心角速度上下波動(dòng),相當(dāng)于在慣性中心角速度上疊加了一個(gè)正弦周期分量,其周期為
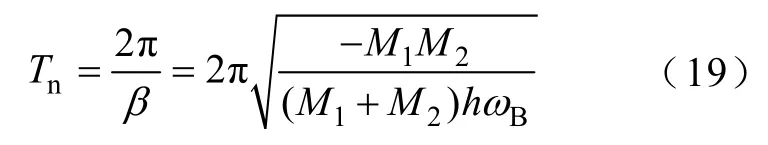
式中,Tn為正弦分量的周期。
標(biāo)幺制下,發(fā)電機(jī)角速度與頻率相等。因此,本文將角速度亦稱為頻率。假設(shè)功率缺額后頻率達(dá)到低頻減載首輪動(dòng)作頻率的時(shí)刻為ts,對(duì)式(13)~式(15)進(jìn)行積分,得ts時(shí)刻各發(fā)電機(jī)頻率及系統(tǒng)慣性中心頻率偏移面積為
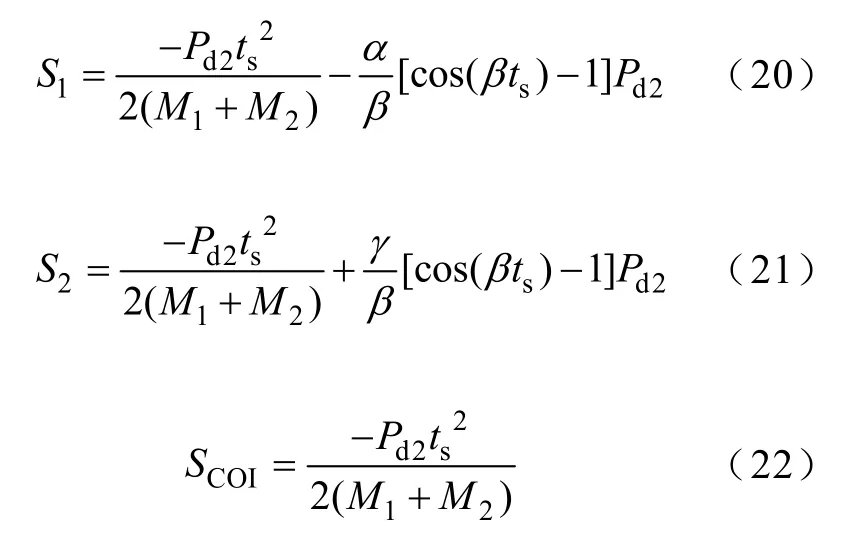
式中,S1、S2、SCOI分別為發(fā)電機(jī)1、發(fā)電機(jī) 2、慣性中心頻率偏移面積。
由式(20)、式(21)可以看出:當(dāng)ts=nTn時(shí),n為整數(shù),各發(fā)電機(jī)與慣性中心頻率偏移面積相等;當(dāng)ts=(n+0.5)Tn時(shí),各發(fā)電機(jī)與慣性中心頻率曲線偏移面積誤差達(dá)到最大值,最大誤差與慣性中心頻率偏移面積比值為
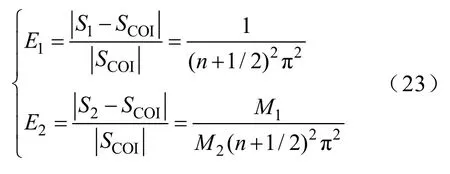
式中,E1、E2為發(fā)電機(jī)1、2最大偏移面積誤差。
低頻減載動(dòng)作前,各發(fā)電機(jī)之間往往會(huì)發(fā)生多次搖擺,并且M1、M2一般處于同一數(shù)量級(jí)。所以,即使是最嚴(yán)重的情況,E1、E2仍較小,可認(rèn)為ts時(shí)刻各發(fā)電機(jī)與慣性中心頻率偏移面積近似相等。因此,本文假設(shè)系統(tǒng)各母線頻率與慣性中心頻率偏移面積近似相等,具有一定的理論依據(jù)。
2.2 系統(tǒng)功率缺額的計(jì)算
忽略網(wǎng)損,擾動(dòng)后系統(tǒng)慣性中心頻率偏移值為
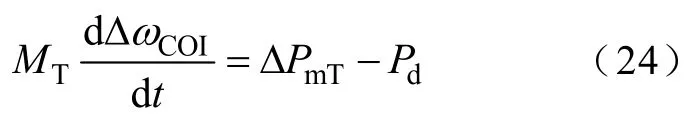
式中,MT為系統(tǒng)總慣性時(shí)間常數(shù);ΔωCOI為慣性中心頻率偏移值;ΔPmT為全部發(fā)電機(jī)總機(jī)械功率增量;Pd為功率缺額,Pd>0表示發(fā)電機(jī)出力不足,Pd<0表示發(fā)電機(jī)出力過(guò)剩,Pd為階躍函數(shù)。對(duì)式(24)進(jìn)行拉氏變換,得
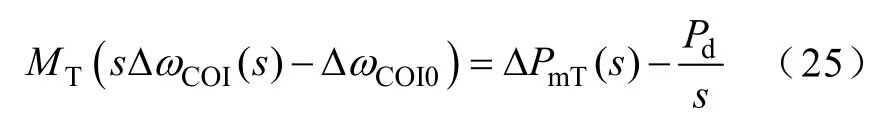
ΔωCOI0=0,式(25)可簡(jiǎn)化為
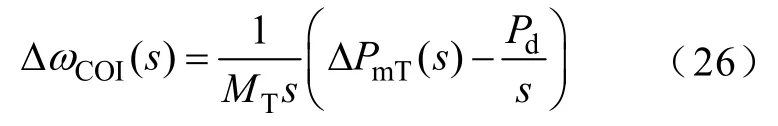
對(duì)系統(tǒng)進(jìn)行單機(jī)等值,建立系統(tǒng)總機(jī)械功率增量與系統(tǒng)慣性中心頻率偏移值之間的傳遞函數(shù)。本文使用 TGOV1模型對(duì)系統(tǒng)進(jìn)行單機(jī)等值[13],系統(tǒng)總機(jī)械功率增量與系統(tǒng)慣性中心頻率偏移值之間的傳遞函數(shù)為
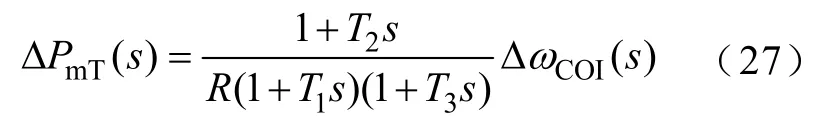
式中,R為系統(tǒng)總頻率調(diào)差系數(shù);T1、T2、T3為 TGOV1模型的時(shí)間常數(shù)。
聯(lián)立式(26)、式(27),計(jì)算擾動(dòng)后系統(tǒng)慣性中心角頻率偏移值為
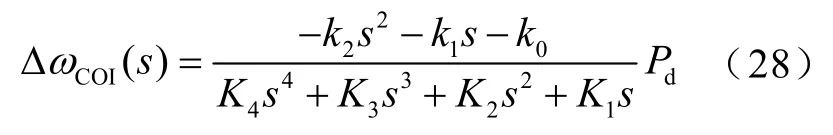
式中,K1=-1;K2=MTR-T2;K3=MTR(T1+T3);K4=MTRT1T3;k0=R;k1=R(T1+T3);k2=RT1T3。
由式(28)可以看出:系統(tǒng)慣性中心頻率偏移值表達(dá)式的特征根由一個(gè)零根和三個(gè)非零根組成,系統(tǒng)慣性中心頻率偏移值的時(shí)域表達(dá)式為
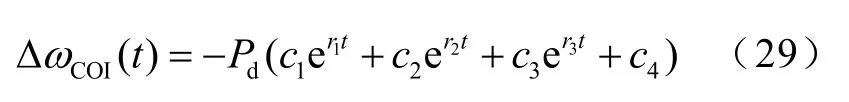
式中,r1、r2、r3為式(28)三個(gè)非零特征根;c1、c2、c3、c4為三個(gè)非零特征根及零根所對(duì)應(yīng)時(shí)域表達(dá)式的系數(shù),并且c1+c2+c3+c4=0。
假設(shè)某母線頻率到達(dá)低頻減載首輪動(dòng)作頻率的時(shí)刻為ts,對(duì)式(29)在 0~ts積分,得慣性中心頻率曲線偏移面積為
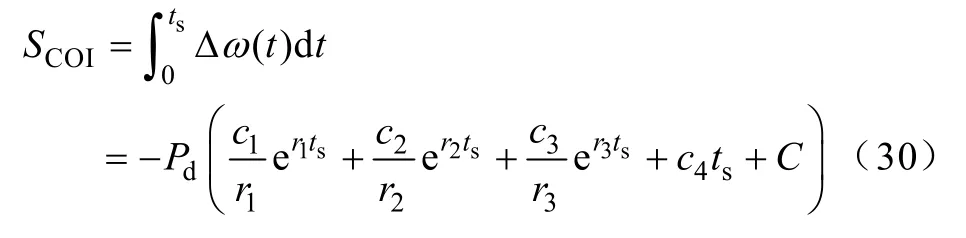
式中,C為常數(shù),且C=-(c1/r1+c2/r2+c3/r3)。
式(30)的物理意義為系統(tǒng)慣性中心頻率偏移曲線在時(shí)間ts處與額定頻率所圍區(qū)域面積,其建立了系統(tǒng)功率缺額與慣性中心頻率偏移面積之間的關(guān)系。由式(30)得到系統(tǒng)功率缺額計(jì)算的表達(dá)式為
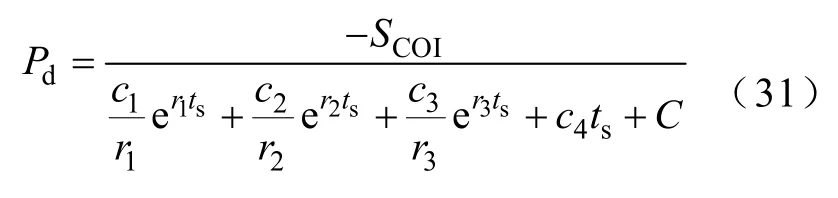
式(27)所描述的系統(tǒng)功率-頻率特性可以通過(guò)定期對(duì)系統(tǒng)進(jìn)行單機(jī)等值、時(shí)域仿真等方式獲取,故式(31)中分母部分除ts外的全部參數(shù)可提前通過(guò)系統(tǒng)分析獲取。低頻減載只需要對(duì)其所安裝母線的頻率及頻率曲線在低頻減載首輪動(dòng)作頻率時(shí)刻的頻率偏移面積進(jìn)行測(cè)量,并記錄該母線頻率到達(dá)低頻減載首輪動(dòng)作頻率的時(shí)刻ts,便可利用式(31)快速計(jì)算系統(tǒng)的功率缺額。
3 基于頻率偏移面積的低頻減載整定
當(dāng)前的低頻減載方案整定后是固定的。對(duì)于大功率缺額事件,低頻減載首輪或前幾輪切負(fù)荷量有可能不足,導(dǎo)致系統(tǒng)頻率恢復(fù)較慢;對(duì)于小功率缺額事件,低頻減載首輪或者前幾輪切負(fù)荷量又有可能過(guò)多,導(dǎo)致低頻減載過(guò)切。
3.1 系統(tǒng)功率缺額算法的啟動(dòng)
本文所提出的基于頻率偏移面積的系統(tǒng)功率缺額計(jì)算程序事先存儲(chǔ)在低頻減載裝置內(nèi)。各低頻減載裝置實(shí)時(shí)測(cè)量其所在母線的頻率,功率缺額計(jì)算算法程序啟動(dòng)條件為

式中,am為系統(tǒng)最大允許頻率下降率,是指無(wú)控制措施時(shí)系統(tǒng)所能承受的最小功率缺額所引起的初始頻率下降率。
最大允許頻率下降系數(shù)am的計(jì)算公式為
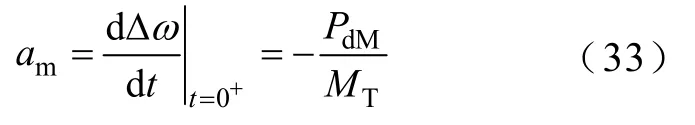
式中,PdM為無(wú)控制措施時(shí)系統(tǒng)所能承受的最大功率缺額;t=0+表示功率擾動(dòng)發(fā)生后的瞬間。
系統(tǒng)最大允許功率缺額PdM可通過(guò)對(duì)系統(tǒng)進(jìn)行單機(jī)等值或者仿真來(lái)獲得,并應(yīng)同時(shí)滿足條件

式中,ΔMω、Δω∞分別為功率缺額事件后,系統(tǒng)頻率偏移的最小值和穩(wěn)態(tài)值;bM、b∞分別為無(wú)頻率穩(wěn)定控制措施時(shí),系統(tǒng)所能承受的頻率偏移和穩(wěn)態(tài)頻率偏移的極限值。
3.2 低頻減載整定方案的設(shè)計(jì)
與當(dāng)前電力系統(tǒng)低頻減載整定方案各輪次切負(fù)荷量一經(jīng)整定便不再變化不同,本文提出根據(jù)功率的缺額大小采取不同的低頻減載整定方案,其基本思想為:當(dāng)功率缺額較大時(shí),低頻減載應(yīng)首先保證系統(tǒng)頻率穩(wěn)定性,盡快恢復(fù)系統(tǒng)功率平衡,此時(shí)低頻減載首輪切負(fù)荷量或者前幾輪切負(fù)荷量應(yīng)大一些,更有利于系統(tǒng)頻率的快速恢復(fù);當(dāng)功率缺額較小時(shí),在保證頻率穩(wěn)定的基礎(chǔ)上可以考慮適當(dāng)降低切負(fù)荷量,此時(shí)低頻減載首輪切負(fù)荷量可適當(dāng)降低一些。
在實(shí)際應(yīng)用中,工程技術(shù)人員可以根據(jù)電網(wǎng)的實(shí)際情況,按照基本思想設(shè)計(jì)各自的低頻減載整定方案。低頻減載輪次由基本輪和特殊輪組成,基本輪一般為3~8輪,本文基本輪采用5輪次,各輪次動(dòng)作頻率差值為 0.2Hz。本文簡(jiǎn)單地以功率缺額占系統(tǒng)總?cè)萘康拇笮橐罁?jù)來(lái)刻畫系統(tǒng)功率缺額的嚴(yán)重程度并進(jìn)行低頻減載的整定,低頻減載整定方案見表1。表中,PT為系統(tǒng)總?cè)萘浚籥%、b%為比例參數(shù),可根據(jù)系統(tǒng)實(shí)際情況選取不同的值。

表1 不同功率缺額的低頻減載方案Tab.1 UFLS schemes for different power deficits
4 算例分析
4.1 基于頻率偏移面積的系統(tǒng)功率缺額計(jì)算
4.1.1 IEEE 39母線系統(tǒng)功率缺額計(jì)算
IEEE 39母線系統(tǒng)總裝機(jī)容量為7961.2MW,總有功負(fù)荷為6150.1MW,總慣性常量為 1565.4。為了構(gòu)造功率缺額事件,在母線4處增加一臺(tái)無(wú)窮大容量發(fā)電機(jī),模擬外部向系統(tǒng)注入的不同功率。通過(guò)設(shè)置母線4處發(fā)電機(jī)退出于運(yùn)行來(lái)構(gòu)造不同功率缺額事件。31、35、36、37、38、39母線發(fā)電機(jī)為調(diào)頻發(fā)電機(jī),各發(fā)電機(jī)調(diào)速器模型均為TGOV1模型,調(diào)速器調(diào)差系數(shù)按各發(fā)電機(jī)容量取5%,調(diào)速器時(shí)間常數(shù)T1、T2、T3分別取 0.5s、1.5s、5.0s。
對(duì)系統(tǒng)進(jìn)行單機(jī)等值,式(31)中各系數(shù)的值見表2。
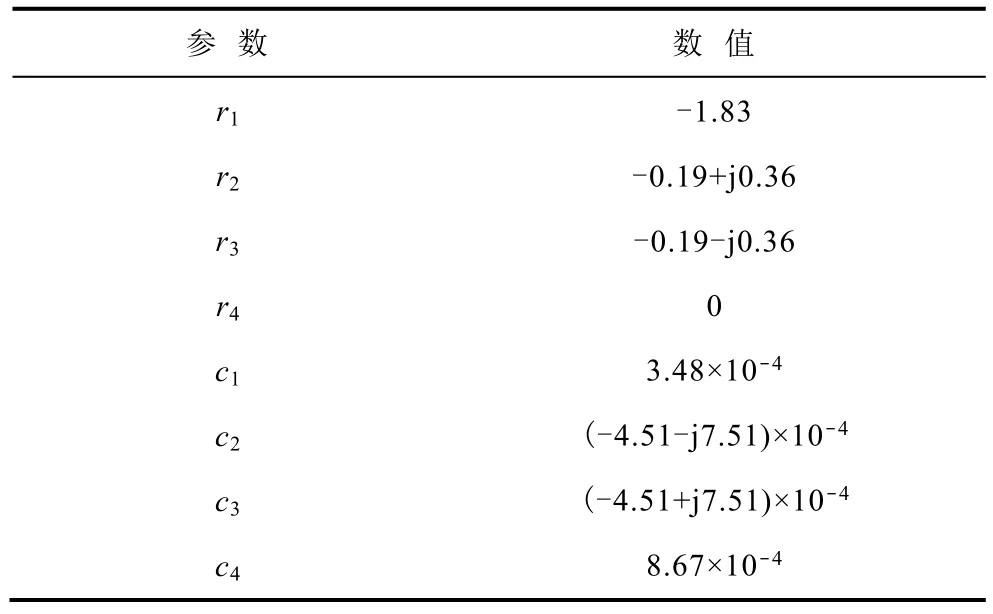
表2 式(31)中各參數(shù)的計(jì)算值Tab.2 The values of parameters in Eqn.(31)
以各母線頻率到達(dá) 59Hz為例,測(cè)量各母線頻率偏移面積并記錄各母線頻率到達(dá)59Hz的時(shí)間ts,當(dāng)系統(tǒng)功率缺額為1500MW時(shí),使用式(31)計(jì)算系統(tǒng)功率缺額,計(jì)算結(jié)果見表3。
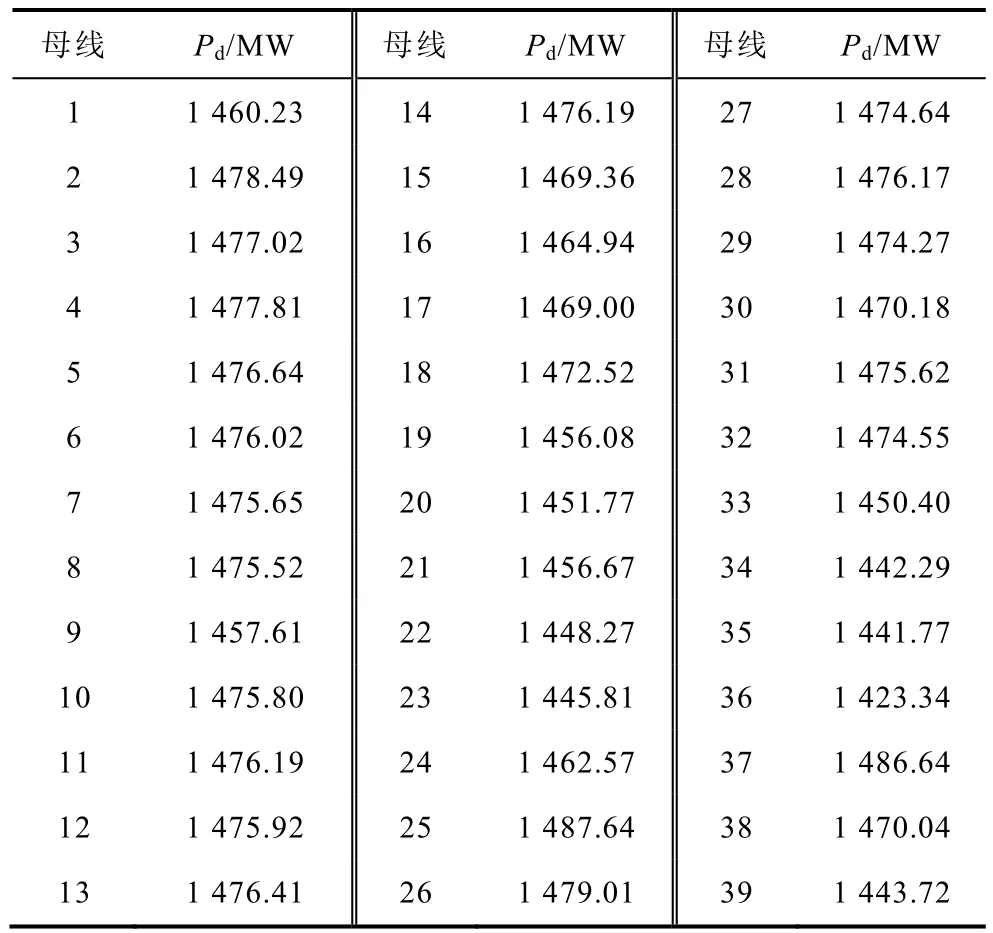
表3 59Hz頻率偏移面積功率缺額計(jì)算Tab.3 Pd calculation using 59Hz deviation area
計(jì)算結(jié)果分析:通過(guò)測(cè)量各母線頻率偏移面積,本文算法均能較好地計(jì)算系統(tǒng)的功率缺額,各母線計(jì)算結(jié)果相近。其中最大誤差為36號(hào)母線計(jì)算結(jié)果,誤差為-76.66MW,占功率缺額的5.1%。全部母線計(jì)算結(jié)果誤差平均值為-35.7MW,占功率缺額的3.57%。
為進(jìn)一步驗(yàn)證本文算法的有效性,使用文獻(xiàn)[7]單機(jī)等值模型、各母線及系統(tǒng)慣性中心初始頻率下降率計(jì)算系統(tǒng)功率缺額。初始頻率下降率與功率缺額計(jì)算公式為
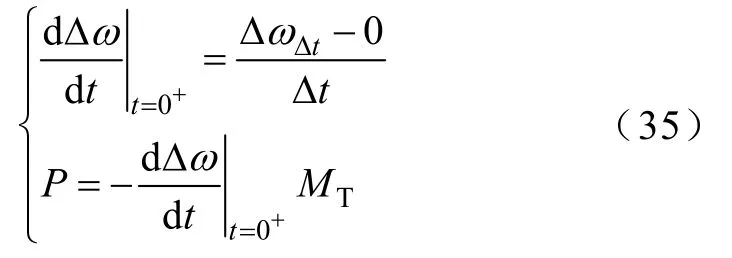
式中,ΔωΔt為功率擾動(dòng)后 Δt時(shí)刻各母線或慣性中心頻率偏移值;Δt為計(jì)算初始頻率下降率的時(shí)間間隔,頻率偏移初始值為0;P為使用各母線或慣性中心始頻率下降率所計(jì)算的功率缺額。
本文中Δt取0.1s,即選取擾動(dòng)后0s和 0.1s兩個(gè)時(shí)刻各母線頻率及慣性中心頻率計(jì)算各母線及系統(tǒng)慣性中心的初始頻率下降率,使用式(35)計(jì)算系統(tǒng)功率缺額,慣性中心初始頻率下降率的計(jì)算結(jié)果為1 507.40MW,各母線初始頻率下降率的計(jì)算結(jié)果見表4。
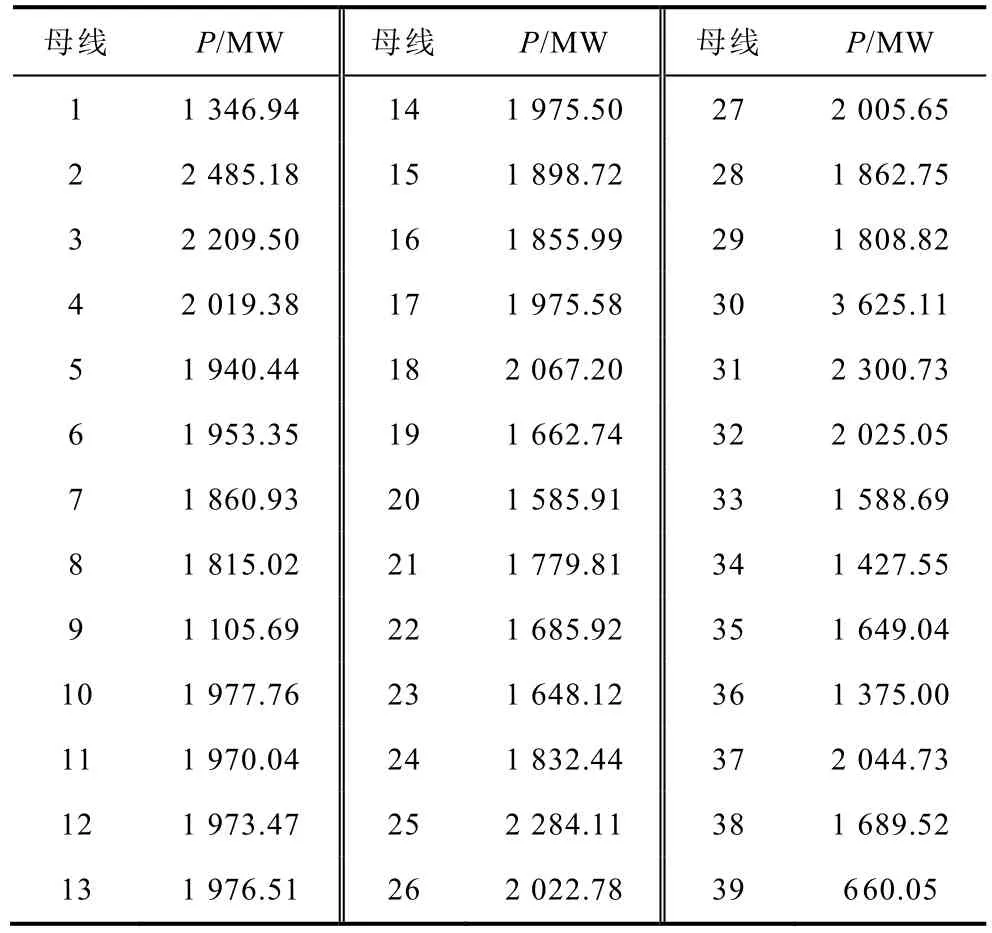
表4 基于初始頻率下降率功率缺額計(jì)算結(jié)果Tab.4 P calculation using initial df/dt
計(jì)算結(jié)果分析:各母線計(jì)算結(jié)果差異較大,計(jì)算結(jié)果分散。原因在于頻率具有時(shí)空分布特性,同一時(shí)刻各母線頻率下降率不同,使用單一母線某一時(shí)刻的頻率下降率,并不能較好地反映系統(tǒng)的功率平衡情況。慣性中心頻率與本文算法均能較好地計(jì)算系統(tǒng)的功率缺額,慣性中心頻率計(jì)算結(jié)果略好于本文算法,但是使用慣性中心頻率計(jì)算系統(tǒng)功率缺額需要廣域通信系統(tǒng)。
下文將進(jìn)一步驗(yàn)證不同頻率時(shí)刻本文算法的有效性。系統(tǒng)功率缺額同樣為1500MW時(shí),分別使用59.2Hz和 58.8Hz時(shí)的部分母線頻率偏移面積計(jì)算系統(tǒng)功率缺額,計(jì)算結(jié)果見表5。
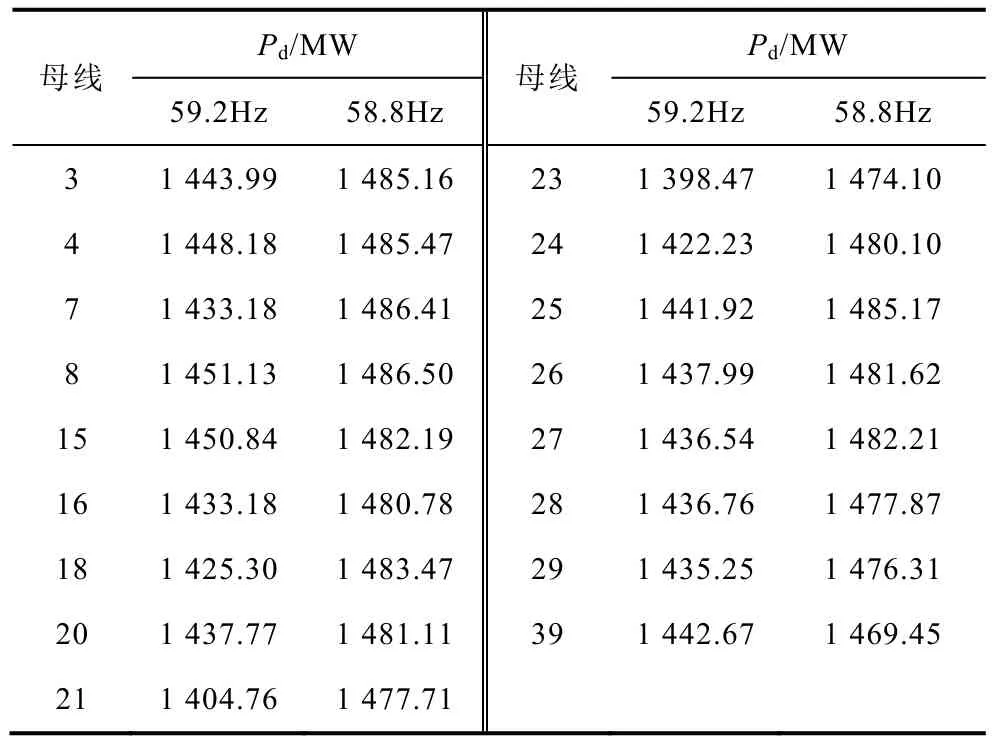
表5 59.2Hz與58.8Hz頻率偏移面積功率缺額計(jì)算Tab.5 Pd calculation using 59.2Hz and 58.8Hz deviation areas
由表 5可以看出:59.2Hz和 58.8Hz頻率偏移面積都能較準(zhǔn)確地計(jì)算功率缺額;計(jì)算結(jié)果為58.8Hz略好于59Hz,59Hz略好于59.2Hz。
驗(yàn)證不同功率缺額時(shí)算法的有效性。系統(tǒng)功率缺額分別為900MW和2000MW時(shí),使用59.2Hz時(shí)頻率偏移面積及慣性中心初始頻率下降率計(jì)算系統(tǒng)功率缺額,慣性中心初始頻率下降率的計(jì)算結(jié)果分別為904.68MW、2 001.01MW,部分母線頻率偏移面積的計(jì)算結(jié)果見表6。
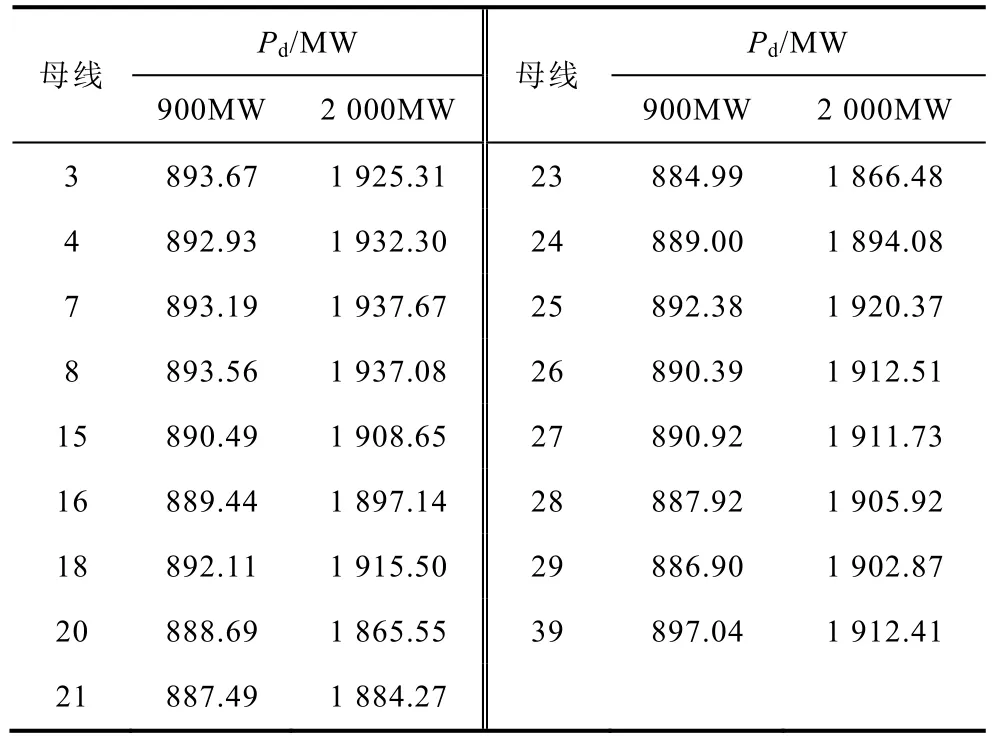
表6 900MW和2000MW功率缺額時(shí)計(jì)算結(jié)果Tab.6 Pd calculation of 900MW and 2000MW deficit
計(jì)算結(jié)果分析:功率缺額為900MW和2000MW時(shí),本文算法及使用慣性中心初始頻率下降率算法依舊能準(zhǔn)確計(jì)算系統(tǒng)的功率缺額。
驗(yàn)證不同負(fù)荷比例時(shí)本文算法的有效性。功率缺額同樣為1500MW時(shí),選取恒阻抗、恒電流及恒功率負(fù)荷比例為 30%、30%、40%,使用 59.2Hz、59Hz頻率偏移面積及慣性中心初始頻率下降率計(jì)算系統(tǒng)功率缺額,慣性中心初始頻率下降率的計(jì)算結(jié)果為1 301.68MW,部分母線頻率偏移面積的計(jì)算結(jié)果見表7。
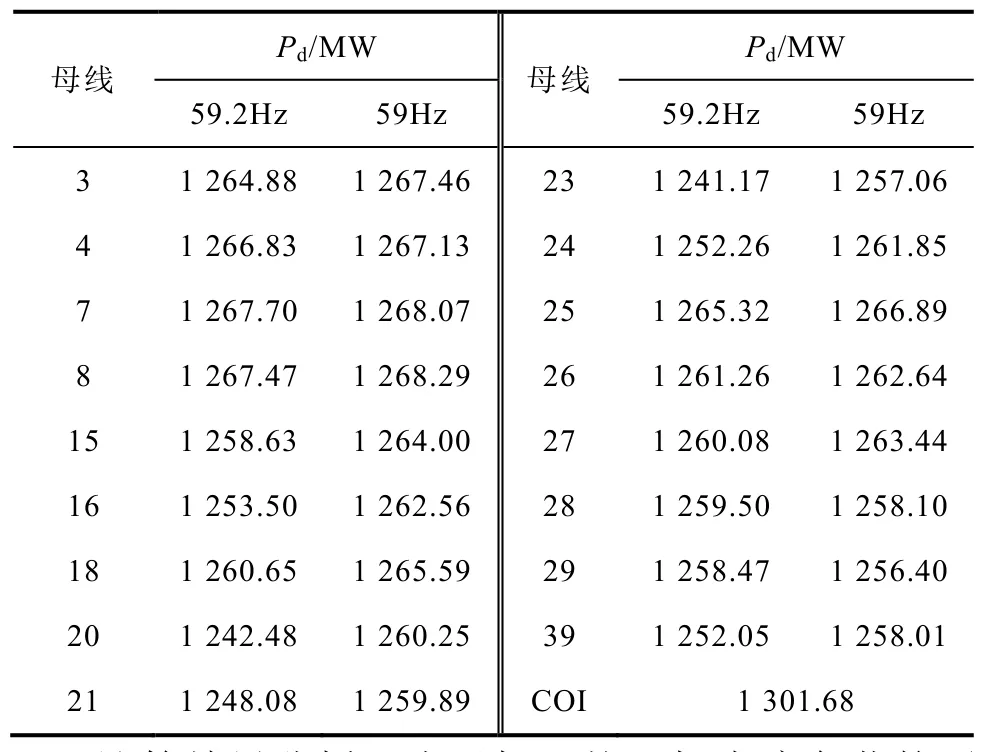
表7 ZIP負(fù)荷功率缺額時(shí)計(jì)算結(jié)果Tab.7 Pd calculation with ZIP load model
計(jì)算結(jié)果分析:由于恒阻抗及恒電流負(fù)荷的壓變效應(yīng),當(dāng)系統(tǒng)發(fā)生功率缺額事件后,實(shí)際負(fù)荷往往變小。所以增加恒阻抗、恒電流負(fù)荷比例后,本文算法及使用慣性中心頻率算法功率缺額計(jì)算結(jié)果都偏小,但仍能較好地計(jì)算系統(tǒng)的功率缺額。
4.1.2 IEEE 145母線系統(tǒng)功率缺額計(jì)算
IEEE 145母線系統(tǒng)來(lái)源于文獻(xiàn)[20],為模擬不同的功率缺額,在117號(hào)母線增加一臺(tái)無(wú)窮大容量電源。系統(tǒng)中,93號(hào)、139號(hào)、145號(hào)母線發(fā)電機(jī)為調(diào)頻發(fā)電機(jī),系統(tǒng)總?cè)萘繛?32141MW,負(fù)荷為27096MW,恒功率與恒阻抗負(fù)荷比例分別為95%與5%。t=0時(shí)117號(hào)母線電源退出運(yùn)行。使用各母線59.2Hz時(shí)頻率偏移面積計(jì)算系統(tǒng)功率缺額。當(dāng)功率缺額分別為 1000MW、1700MW及2500MW時(shí),輸出誤差最大的 30個(gè)母線計(jì)算結(jié)果見表 8~表 10。
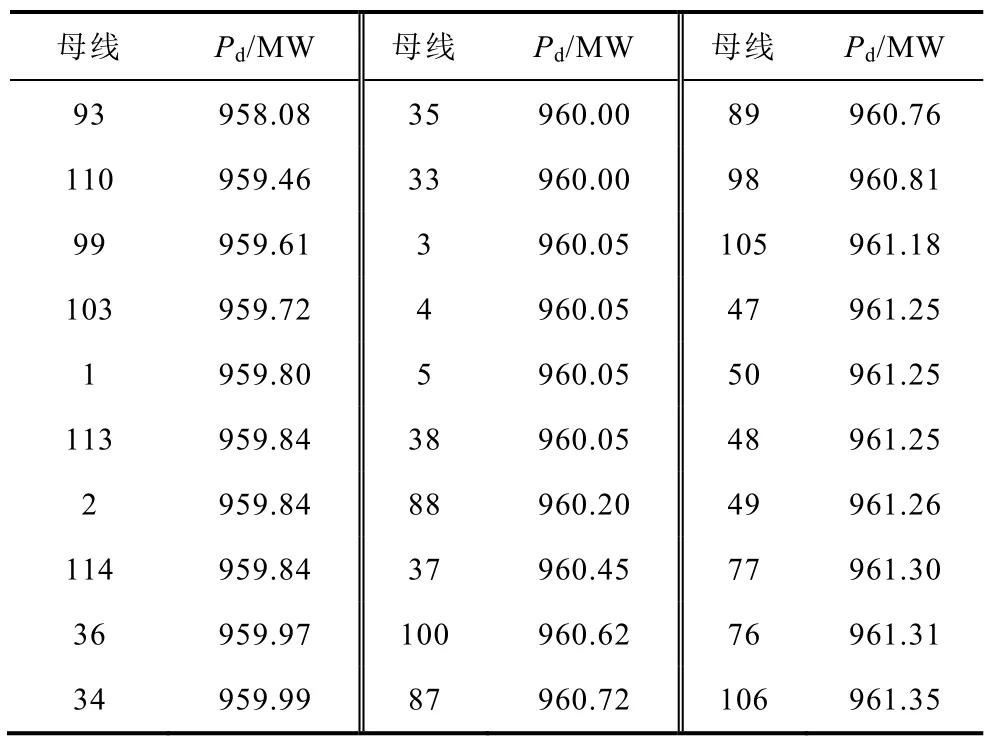
表8 1000MW功率缺額時(shí)計(jì)算結(jié)果Tab.8 Pd calculation with 1000MW deficit
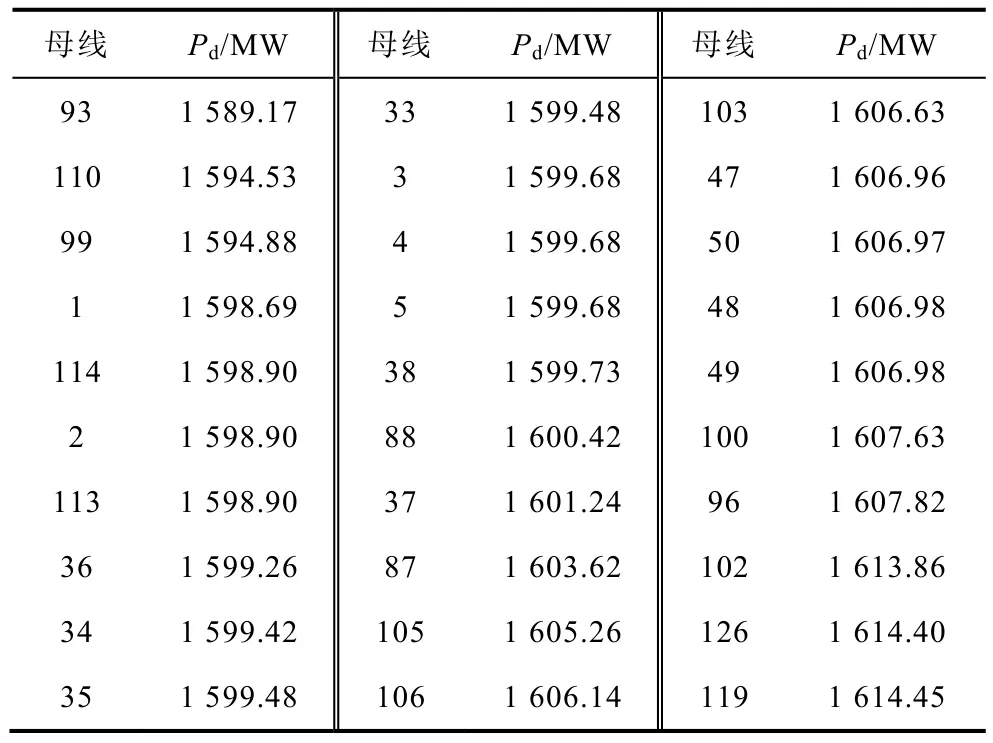
表9 1700MW功率缺額時(shí)計(jì)算結(jié)果Tab.9 Pd calculation with 1700MW deficit
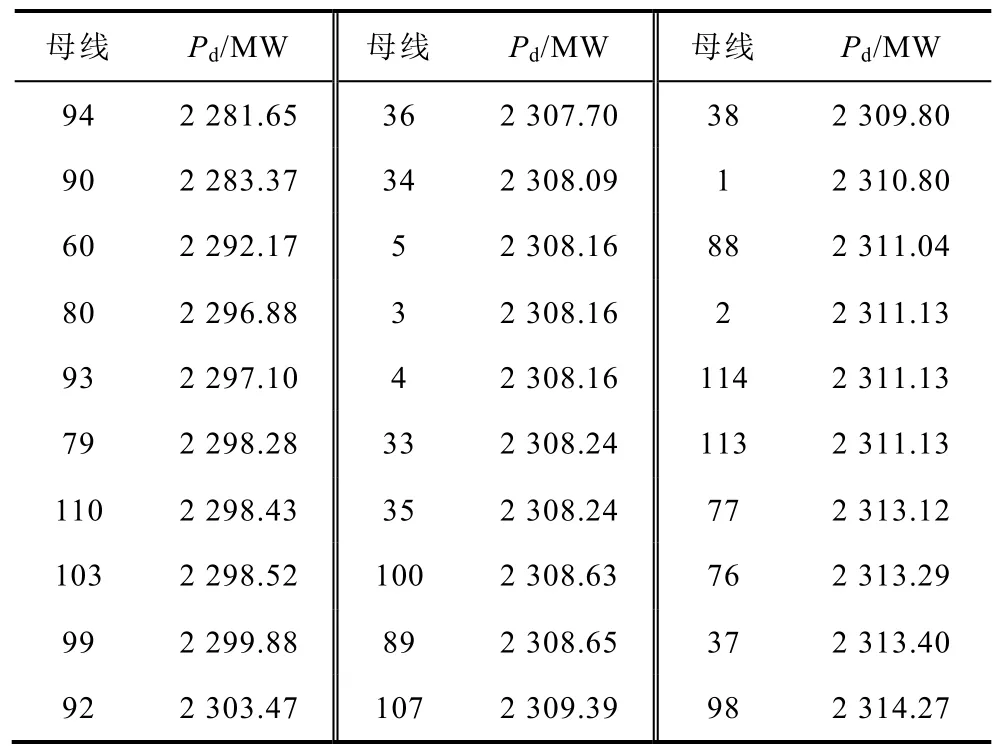
表10 2500MW功率缺額時(shí)計(jì)算結(jié)果Tab.10 Pd calculation with 2500MW deficit
由表8計(jì)算結(jié)果可知:功率缺額為1000MW時(shí),計(jì)算結(jié)果最大誤差為93號(hào)母線,誤差為-41.92MW,占功率缺額的 4.19%。全部母線計(jì)算結(jié)果誤差平均值為-35.7MW,占功率缺額的3.57%。
由表9計(jì)算結(jié)果可知:功率缺額為1700MW時(shí),計(jì)算結(jié)果最大誤差為93號(hào)母線,誤差為-110.83MW,占功率缺額的 6.52%。全部母線計(jì)算結(jié)果誤差平均值為-77MW,占功率缺額的4.5%。
由表10計(jì)算結(jié)果可知:功率缺額為2500MW時(shí),計(jì)算結(jié)果最大誤差母線為 94號(hào)母線,誤差為-218.35MW,占功率缺額的8.73%。全部母線計(jì)算結(jié)果誤差平均值為-159.65MW,占功率缺額的 6.4%。
當(dāng)系統(tǒng)實(shí)際功率缺額為1000MW、1700MW及2500MW 時(shí),使用文獻(xiàn)[7]算法計(jì)算系統(tǒng)功率缺額,并與本文算法進(jìn)行對(duì)比,結(jié)果見表11。
由表11計(jì)算結(jié)果可知:本文算法均能準(zhǔn)確計(jì)算系統(tǒng)功率缺額,計(jì)算準(zhǔn)確性均好于文獻(xiàn)[7]。
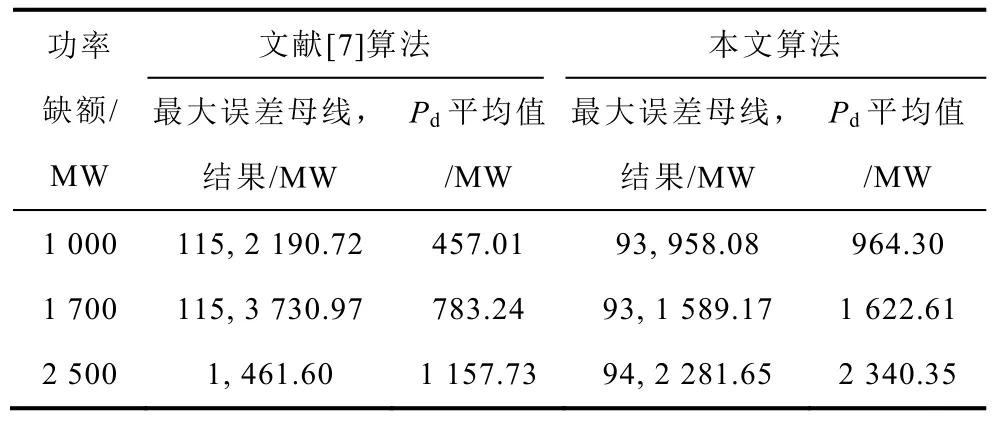
表11 文獻(xiàn)[7]算法與本文算法計(jì)算結(jié)果對(duì)比Tab.11 Algorithm comparisons in Ref.[7]and this paper
4.2 基于頻率偏移面積的低頻減載整定
4.2.1 IEEE 39母線系統(tǒng)低頻減載方案驗(yàn)證
對(duì)比本文方法、傳統(tǒng)法及自適應(yīng)法三種低頻減載方案。選取功率缺額占系統(tǒng)總?cè)萘勘壤謩e為15%≥Pd/PT、25%≥Pd/PT≥15%、Pd/PT≥25%,對(duì)應(yīng)功率缺額為 900MW、1500MW、2000MW三種情況。在除12號(hào)母線外所有負(fù)荷母線安裝低頻減載裝置,切負(fù)荷總量在低頻減載間的分配比例見表 12。
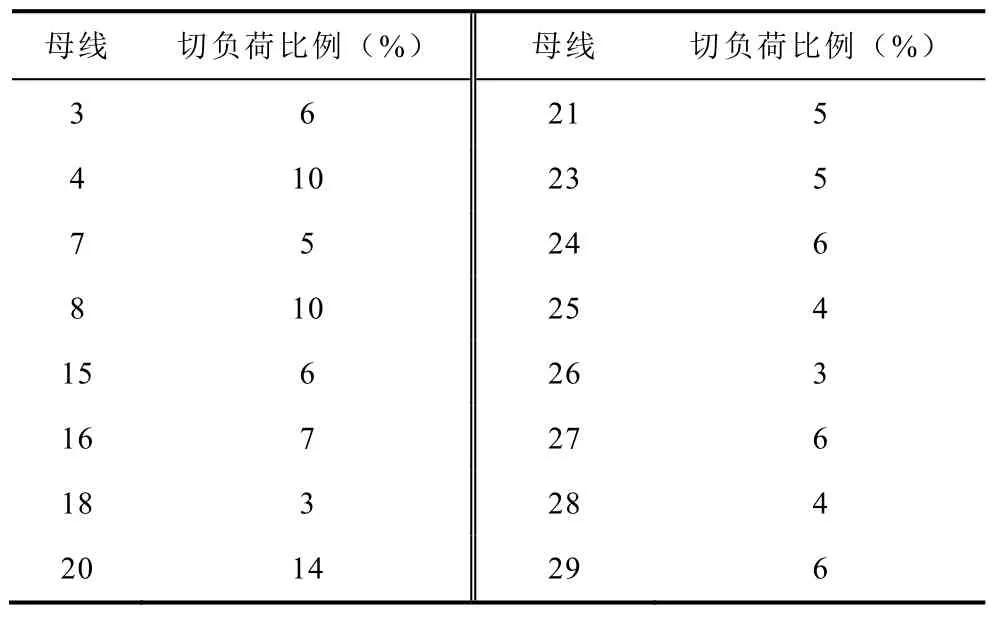
表12 切負(fù)荷總量在各低頻減載間的分配比例Tab.12 The ratio of total load shed of every bus
各低頻減載方案首輪動(dòng)作頻率均為59.2Hz,動(dòng)作輪次均為 5輪,各輪次級(jí)差均為 0.2Hz,動(dòng)作延遲均為 0.1s。傳統(tǒng)法采取系統(tǒng)可能出現(xiàn)的最大功率缺額,即39號(hào)母線發(fā)電機(jī)退出,導(dǎo)致系統(tǒng)最大功率缺額為1500MW,各低頻減載方案見表13。
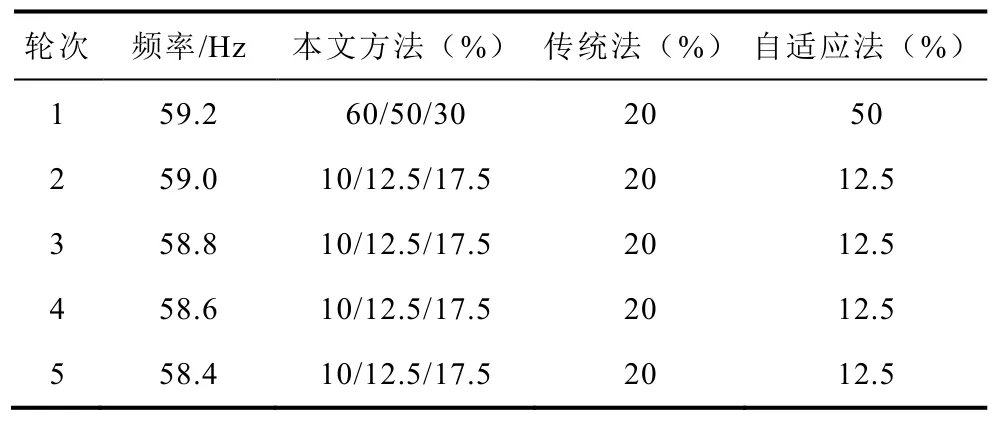
表13 低頻減載整定方案Tab.13 Different strategies of UFLS
仿真測(cè)試不同功率缺額情況下三種低頻減載方案的動(dòng)作輪次、切負(fù)荷量見表14,低頻減載動(dòng)作后的系統(tǒng)慣性中心頻率曲線,如圖5~圖7所示。
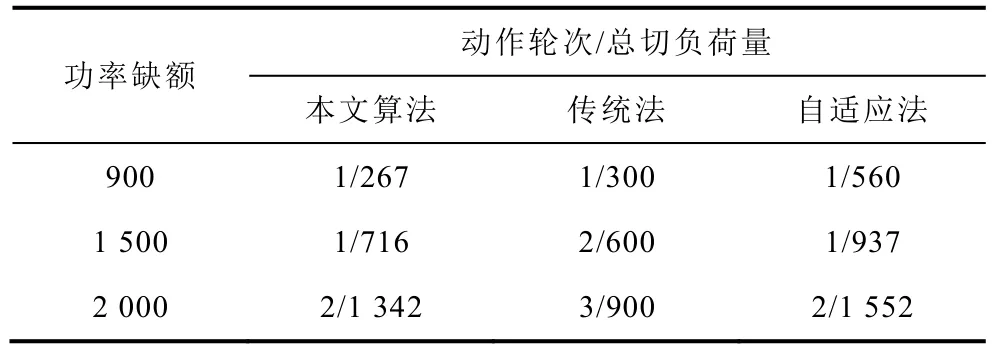
表14 低頻減載動(dòng)作輪次及切負(fù)荷量Tab.14 Load shedding steps and amounts of UFLS(單位:MW)
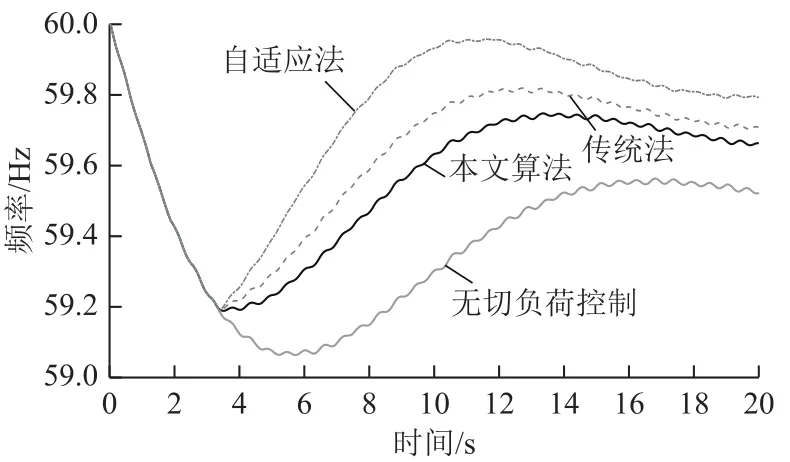
圖5 900MW功率缺額時(shí)頻率曲線Fig.5 Frequency curves of 900MW deficit
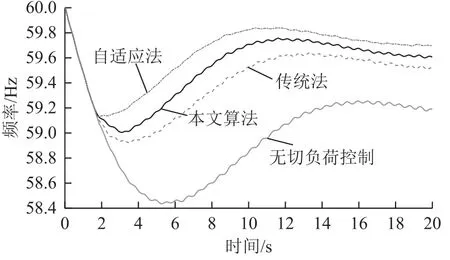
圖6 1500MW功率缺額時(shí)頻率曲線Fig.6 Frequency curves of 1500MW deficit
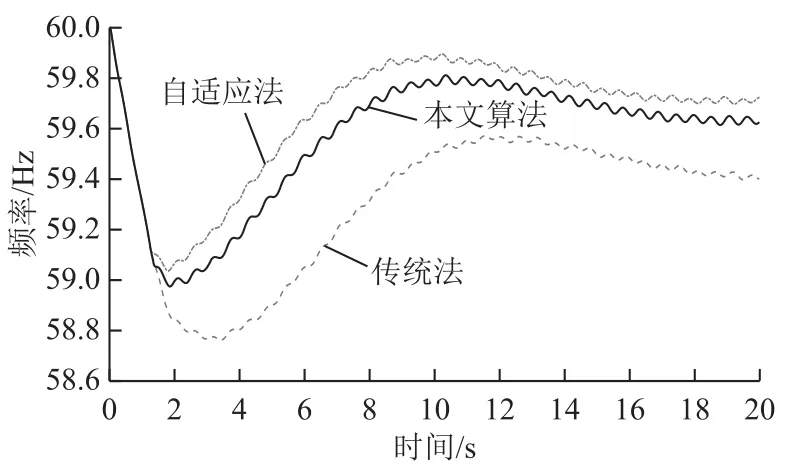
圖7 2000MW功率缺額時(shí)頻率曲線Fig.7 Frequency curves of 2000MW deficit
在三種功率缺額下,自適應(yīng)法切負(fù)荷量均大于本文方法。功率缺額為900MW時(shí),三種方案均動(dòng)作1輪,系統(tǒng)頻率最低值均為59.18Hz,本文算法切負(fù)荷量最少;功率缺額為1 500MW時(shí),本文方法最低頻率為59.02Hz,自適應(yīng)法最低頻率為 59.18Hz,傳統(tǒng)法最低頻率為58.9Hz,本文方法切負(fù)荷量小于自適應(yīng)法,頻率恢復(fù)速度優(yōu)于傳統(tǒng)法;功率缺額為2 000MW時(shí),本文方法及自適應(yīng)法均動(dòng)作2輪,傳統(tǒng)法動(dòng)作3輪,本文方法切負(fù)荷量小于自適應(yīng)法,頻率恢復(fù)速度優(yōu)于傳統(tǒng)法。
4.2.2 IEEE 145母線系統(tǒng)低頻減載方案驗(yàn)證
IEEE 145母線系統(tǒng)負(fù)荷母線數(shù)量為80,選取負(fù)荷大于100MW的44個(gè)母線安裝低頻減載裝置,切負(fù)荷量按照各母線負(fù)荷比例分配。傳統(tǒng)法采用系統(tǒng)最大功率缺額為2500MW,選取表 13中低頻減載方案,功率缺額為1000MW、1700MW、2500MW,低頻減載動(dòng)作輪次、切負(fù)荷量見表15,各方案的系統(tǒng)慣性中心頻率曲線如圖8~圖10所示。
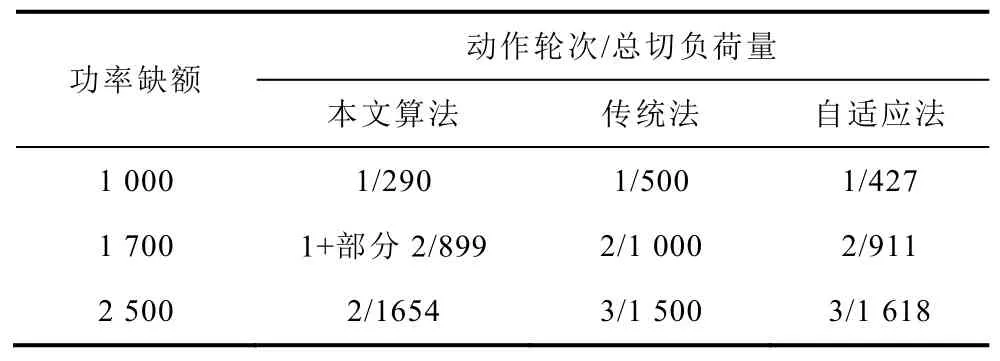
表15 低頻減載動(dòng)作輪次及切負(fù)荷量Tab.15 Load shedding steps and amounts of UFLS(單位:MW)
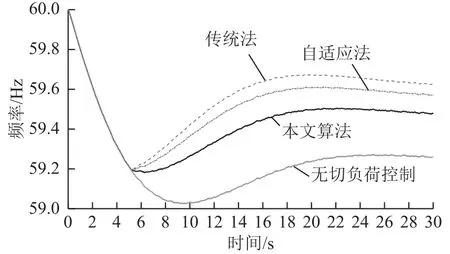
圖8 1000MW功率缺額時(shí)頻率曲線Fig.8 Frequency curves of 1000MW deficit
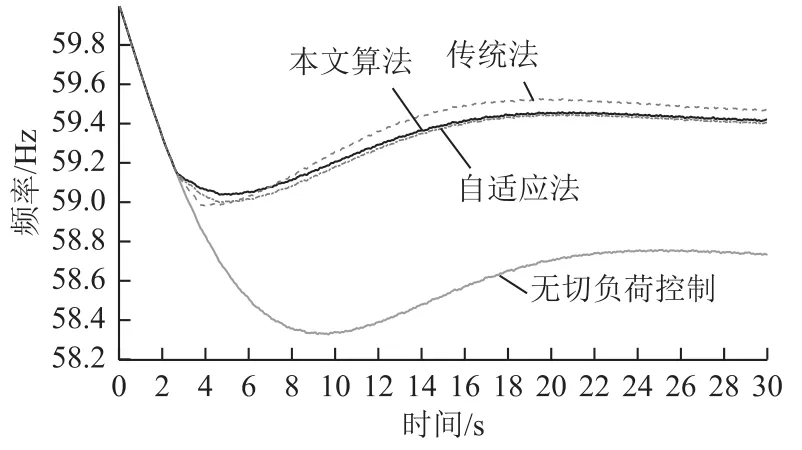
圖9 1700MW功率缺額時(shí)頻率曲線Fig.9 Frequency curves of 1700MW deficit
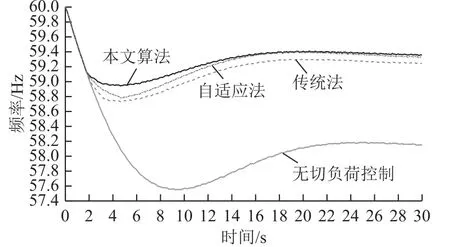
圖10 2500MW功率缺額時(shí)頻率曲線Fig.10 Frequency curves of 2500MW deficit
功率缺額為1000MW時(shí),三種方案均動(dòng)作1輪,最低頻率近似相等,在保證頻率穩(wěn)定的基礎(chǔ)上,本文方法切負(fù)荷量相對(duì)較少;功率缺額為1700MW時(shí),本文方法低頻減載首輪全部動(dòng)作,部分低頻減載動(dòng)作2輪,傳統(tǒng)法和自適應(yīng)法均動(dòng)作2輪,本文方法最低頻率高于自適應(yīng)法和傳統(tǒng)法,并且切負(fù)荷量最小;功率缺額為2500MW時(shí),本文方法動(dòng)作2輪,傳統(tǒng)法和自適應(yīng)法均動(dòng)作3輪,本文方法最低頻率均高于傳統(tǒng)法和自適應(yīng)法,頻率恢復(fù)速度最快。
5 結(jié)論
本文建立頻率偏移面積與系統(tǒng)功率缺額之間的關(guān)系,準(zhǔn)確計(jì)算系統(tǒng)的功率缺額,提出了基于功率缺額大小的低頻減載整定基本思想及方案。應(yīng)用時(shí),工程技術(shù)人員可根據(jù)實(shí)際情況,調(diào)整功率缺額的計(jì)算時(shí)刻、低頻減載各輪次動(dòng)作頻率及切負(fù)荷量。本文得到以下結(jié)論:
1)以簡(jiǎn)化的兩機(jī)系統(tǒng)推導(dǎo)了各發(fā)電機(jī)頻率偏移面積與系統(tǒng)慣性中心頻率偏移面積之間的關(guān)系,得到在低頻減載首輪頻率時(shí)刻母線頻率偏移面積與慣性中心頻率偏移面積近似相等的結(jié)論,并提出基于頻率偏移面積的系統(tǒng)功率缺額計(jì)算算法。算例分析表明,該算法能夠準(zhǔn)確地計(jì)算系統(tǒng)的功率缺額。
2)基于各母線功率缺額的準(zhǔn)確計(jì)算,提出基于功率缺額大小的低頻減載整定基本思想及方案。算例分析表明,所提出的思路與方案在防止系統(tǒng)最低頻率過(guò)低、加快頻率恢復(fù)速度及降低切負(fù)荷量方面具有一定的優(yōu)勢(shì)。
- 電工技術(shù)學(xué)報(bào)的其它文章
- 直線電機(jī)設(shè)計(jì)、控制及系統(tǒng)集成專題特約主編寄語(yǔ)
- 內(nèi)置式永磁電機(jī)轉(zhuǎn)子硅鋼片疊裝錯(cuò)位對(duì)氣隙磁場(chǎng)的影響
- 具備電壓補(bǔ)償功能的不停電過(guò)分相系統(tǒng)及控制方法
- 基于狀態(tài)估計(jì)的高速受電弓魯棒預(yù)測(cè)控制
- 電氣化鐵路牽引變電所群貫通供電系統(tǒng)及其關(guān)鍵技術(shù)
- 磁控式并聯(lián)電抗器容量調(diào)節(jié)暫態(tài)過(guò)程及其對(duì)匝間保護(hù)的影響

