超聲波燃氣表矩形流道的雷諾修正系數仿真研究

何明昊, 楊 鳴

超聲波燃氣表矩形流道的雷諾修正系數仿真研究

何明昊, 楊 鳴*

（寧波大學 信息科學與工程學院, 浙江 寧波 315211）

在超聲波流量計測量技術中, 雷諾修正系數相關的研究對于提高計量精度有重要作用. 為研究矩形流道的雷諾修正系數與雷諾數的關系, 對矩形流道在常溫常壓流量較小情況下進行仿真, 結果發現: 矩形流道層流狀態下的雷諾修正系數與雷諾數呈線性相關. 保持壓強、體積流量不變, 在不同溫度下進行仿真及擬合, 結果表明: 在不同溫度下雷諾修正系數與雷諾數的線性關系依然滿足. 在上述實驗基礎上, 對矩形流道湍流狀態下的雷諾修正系數與雷諾數關系進行研究, 通過改變溫度、壓強和體積流量進行仿真及擬合發現, 矩形流道湍流狀態下雷諾修正系數與雷諾數呈非線性相關.

超聲波燃氣表; 矩形流道; 雷諾數; 雷諾修正系數

近年來, 超聲波燃氣表的發展十分迅速. 相較于傳統的燃氣表, 超聲波燃氣表具有測量精度高、壓損小、量程比大、適用氣體范圍廣等優點[1]. 過去超聲波燃氣表以圓形流道為主. 近幾年, 日本松下公司率先將矩形流道應用于家用超聲波燃氣表中, 隨后我國杭州威星、遼寧思凱等國內燃氣表公司也開始研發矩形流道產品, 目前矩形流道已被大量應用于超聲波燃氣表. 因此, 如何提升矩形流道下燃氣表的測量精度是超聲波燃氣表研發的關鍵. 雷諾修正系數是超聲波燃氣表中一種與流量測量精度相關的補償系數, 對提升流量測量精度有關鍵作用[2-3]. 但目前國內外關于矩形流道雷諾修正系數的研究仍較為鮮見.

本文基于計算流體力學(Computational Fluid Dynamics, CFD)構建矩形流道模型, 通過CFD模擬仿真與擬合分析相結合, 研究矩形流道層流狀態下雷諾修正系數與雷諾數關系、溫度對矩形流道層流狀態下的雷諾修正系數與雷諾數關系的影響, 以及矩形流道湍流狀態下的雷諾修正系數與雷諾數關系, 以期為提高矩形流道燃氣表的流量測量精度提供參考.

1 超聲波流量計原理

現階段超聲波燃氣表的流速測量方法以時差法為主, 在流道上下游分別安裝超聲波換能器, 以發射和接收換能器之間的連線作為超聲波信號傳播路徑[4-5]. 圖1為時差法超聲波燃氣表測量原理.

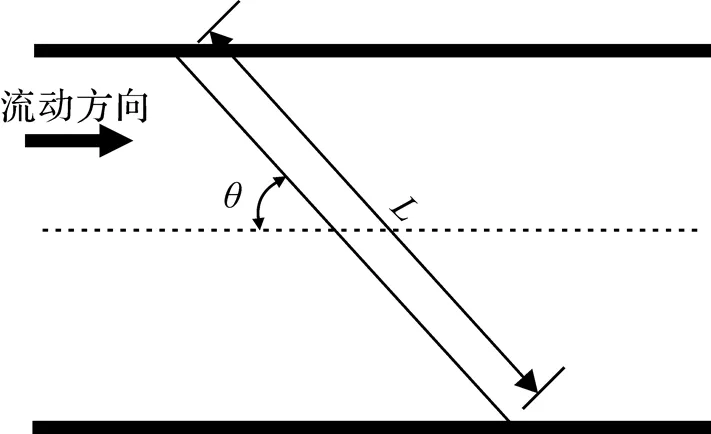
圖1 時差法超聲波燃氣表測量原理

超聲波信號在順流方向傳播時間up、在逆流方向傳播時間dn的計算公式分別為:

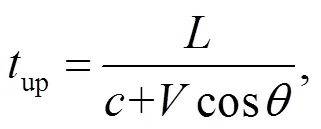
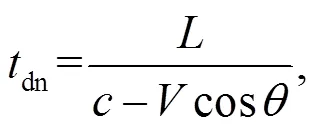
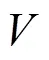
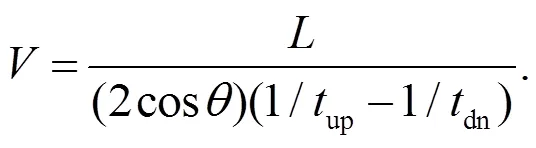
2 矩形流道模型設置

在超聲波燃氣表的流量計量中, 上下游超聲波換能器之間的對應區域即為聲道區域, 流體在此聲道區域中流動. 而圓形流道的管徑較大, 聲波覆蓋面較小, 導致測量結果有偏差, 因此選用矩形流道, 流道狹窄, 聲波能覆蓋整個模型寬度, 可以更加準確地測量流體的流量.

通過建模軟件Creo 2.0建立矩形流道模型, 如圖2所示. 矩形流道截面長12mm、寬50mm, 流道長度100mm, 隔板厚度0.3mm, 隔板與隔板、隔板與流道壁間隔均為2.775mm. 在圓形流道中, 通過安裝流速分布器對流體進行整流, 可使流體分布更加均勻, 更適合測量. 而矩形流道尺寸較小,無法安裝流速分布器, 因此需要在其中安裝等間距隔板以達到整流效果[6].

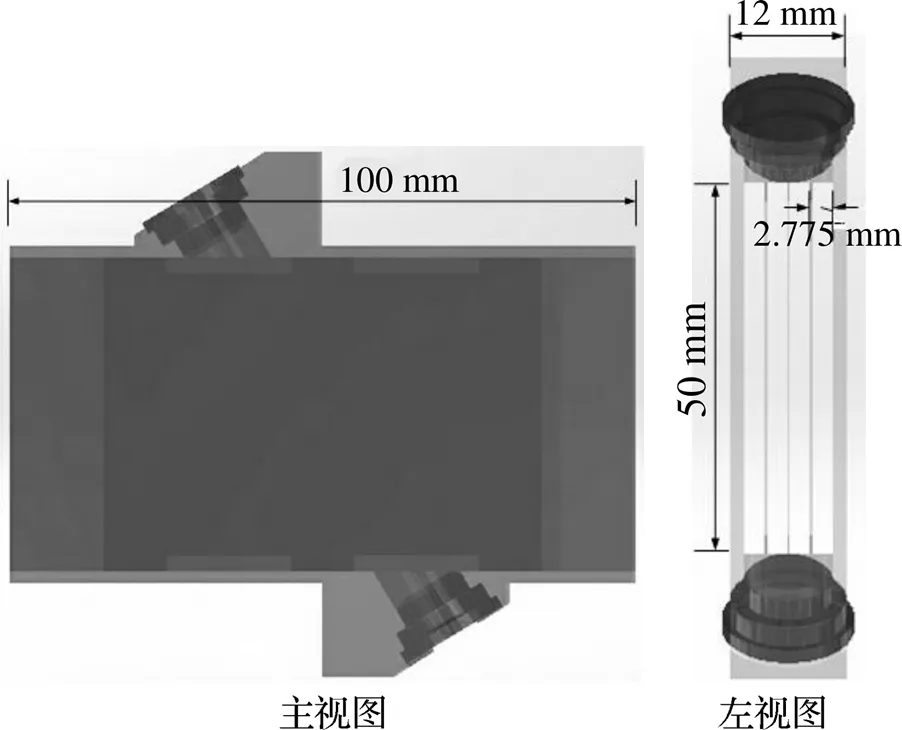
圖2 矩形流道模型

雷諾數()的大小決定了流體的流動狀態與流速分布[7]. 當小于2300時, 流體為層流狀態; 當大于4000時, 流體為湍流狀態; 當介于兩者之間時, 為過渡狀態, 一般作為湍流狀態處理.計算公式為:

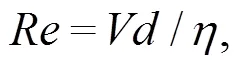
從圖3可知, 矩形流道中氣體流速分布均勻, 在隔板所劃分的局部流道內氣體均為層流狀態, 隔板能夠實現整流. 但對矩形流道應考慮中間部分流速的影響, 因此在模型線平面流道中間設置4段連線作為分割段(圖4).

圖3 矩形流道流速分布

圖4 矩形流道分割段

計算流體力學是流體力學與計算機的結合, 以計算機為工具, 對流體力學中非理想情況進行模擬仿真, 其結果能夠直觀有效地反映流體的流動狀態[10-11]. 研究雷諾修正系數需要結合流體的流動狀態, 而實際流量標定裝置并不能直觀地反映流道內流體的流動狀態[12].

在對上述矩形流道設置基礎上進行模擬仿真. 將模型導入FloEFD仿真軟件, 邊界條件為溫度20℃、壓強10kPa、入口體積流量6.00m3·h-1, 得到4個分割段上的流速分布(圖5).

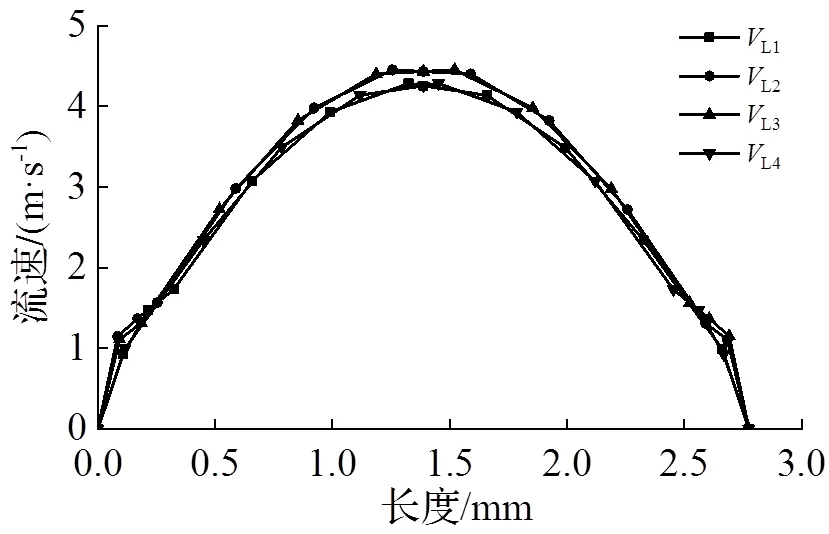
圖5 體積流量6.00 m3·h-1時流速分布

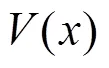
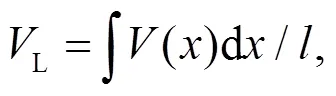
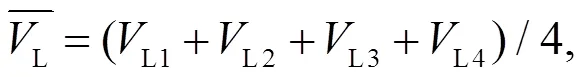
式中:L1、L2、L3、L4分別為4個分割段根據式(6)計算得到的每個分割段上的線平均流速.

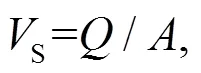
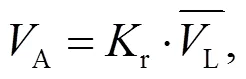
3 擬合分析

3.1 矩形流道層流狀態下雷諾修正系數

當小于2300時, 流道中氣體為層流狀態, 如圖6所示, 氣體流動平穩, 流速分布均勻.

圖6 矩形流道在層流狀態下的流速分布

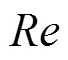
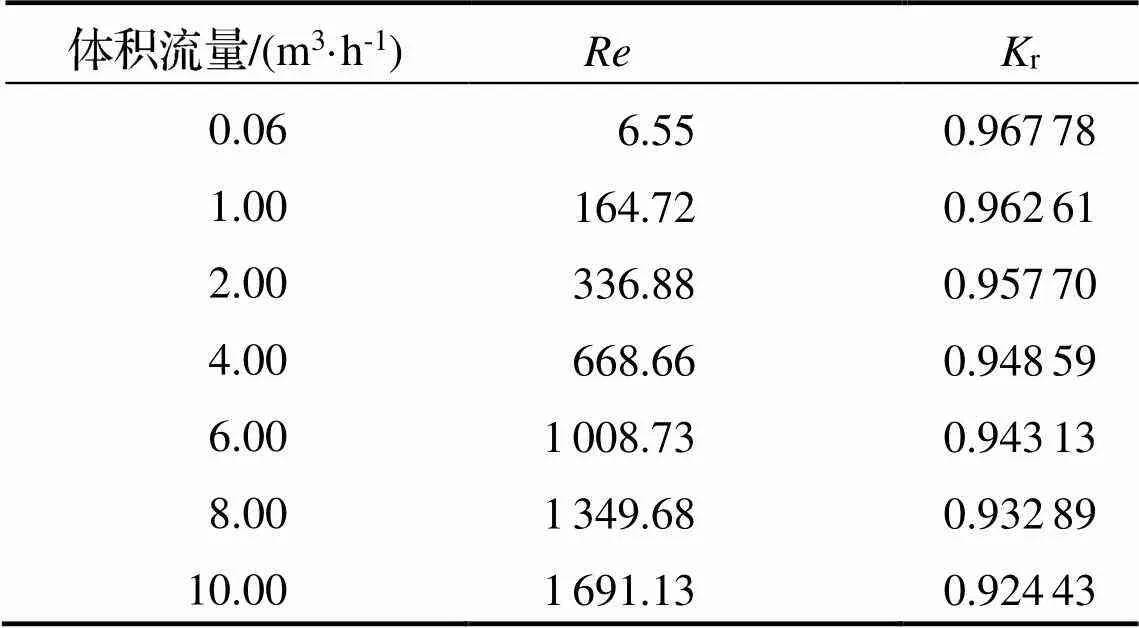
表1 20℃、10kPa條件下Re與Kr值

從表1可知, 當體積流量處于最大值10.00 m3·h-1以下時,均小于2300, 氣體處于層流狀態. 通過最小二乘法擬合得出矩形流道在20℃、10kPa條件下r與關系(圖7).

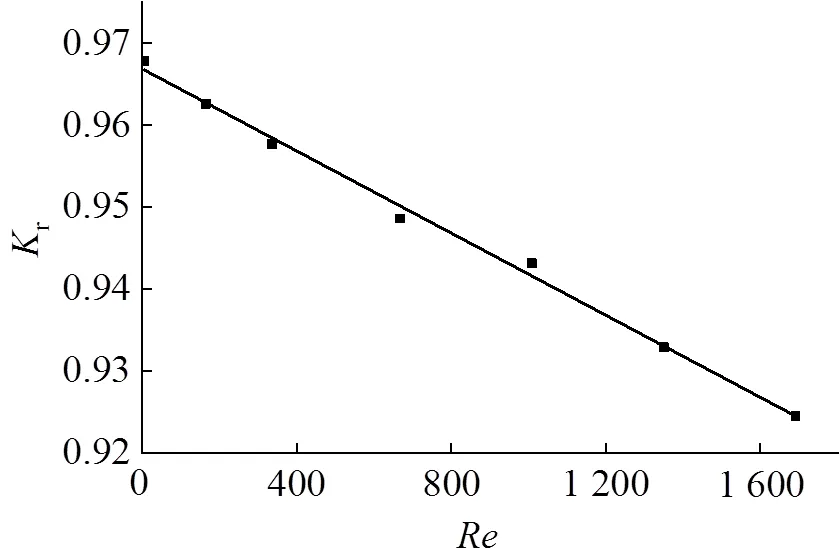
圖7 層流狀態下Kr與Re關系

由圖7擬合結果可知,r與關系為:

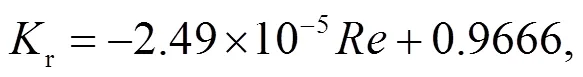
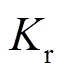
3.2 矩形流道層流狀態下對溫度的適應性

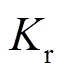
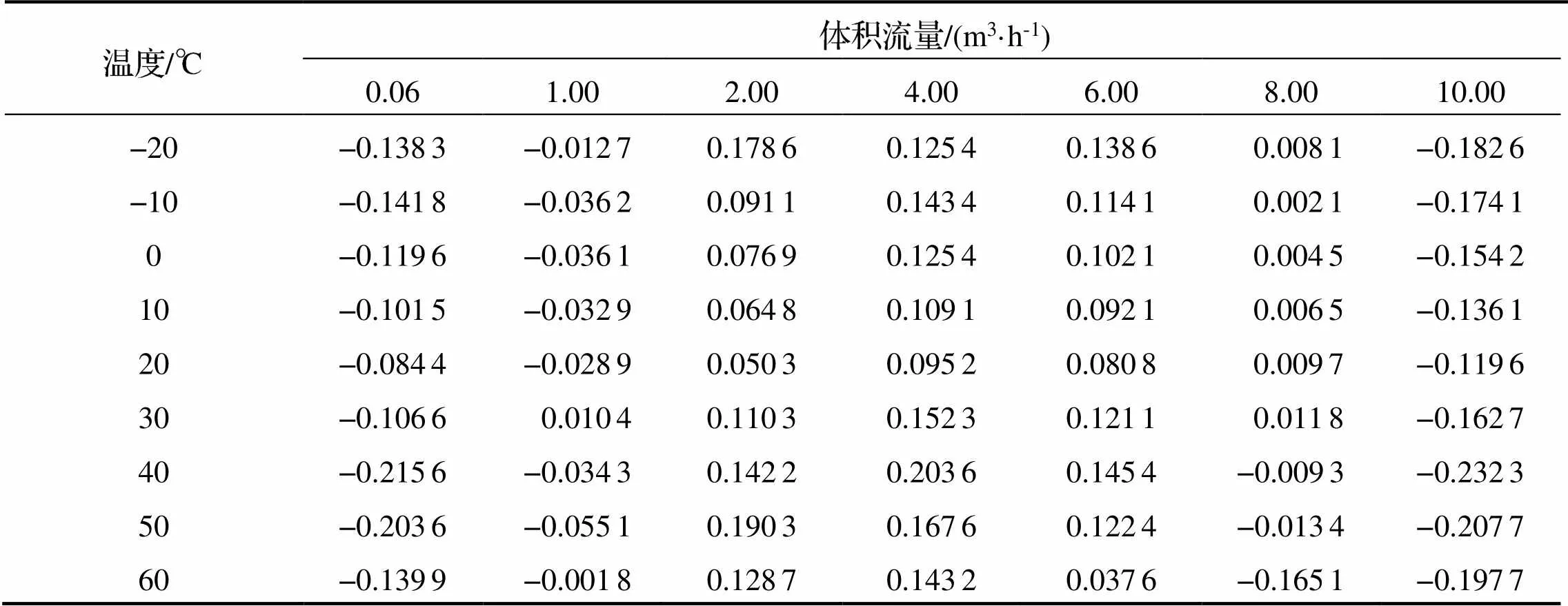
表2 不同溫度條件下面平均流速的相對誤差 %

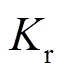
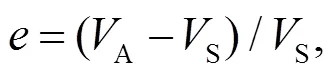
根據式(10)計算得出矩形流道在不同溫度條件下不同流量時值(表2).

從圖9可知, 在-20~60℃溫度條件下矩形流道相對誤差滿足測量標準. 隨著矩形流道內體積流量增加, 在0.06~4.00m3·h-1范圍內, 不同溫度下相對誤差曲線皆呈上升趨勢, 在4.00~10.00m3·h-1范圍內皆呈下降趨勢, 而在不同溫度條件下相對誤差曲線的幅值不同, 表明溫度對矩形流道層流狀態下r與關系的相對誤差曲線幅值存在影響.

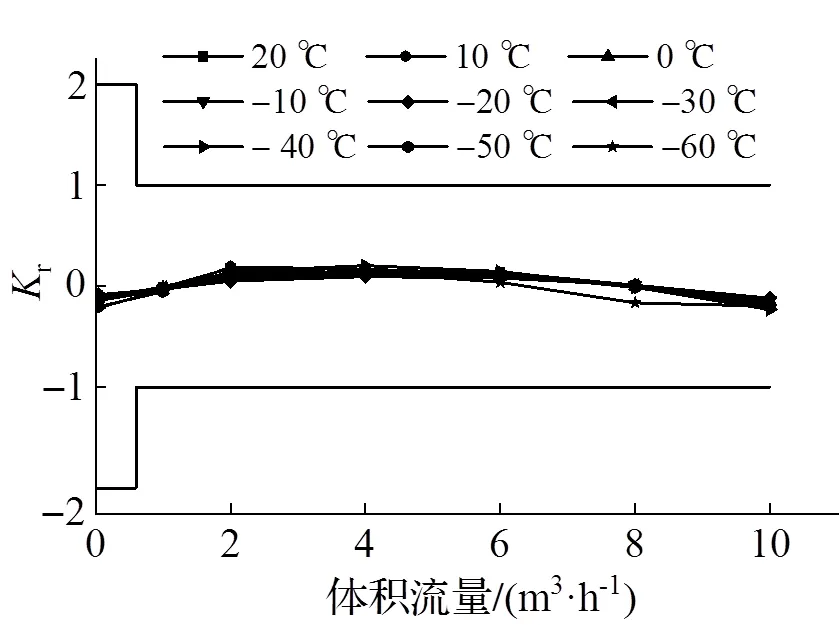
圖9 矩形流道在不同溫度條件下的相對誤差曲線

3.3 矩形流道湍流狀態下分析

當大于4000時, 氣體在流道中為湍流狀態, 流道中存在小漩渦, 流速分布不均勻(圖10).

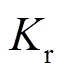
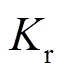
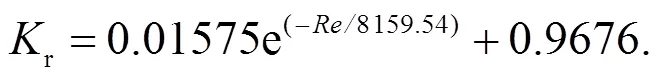
函數圖像如圖11所示.

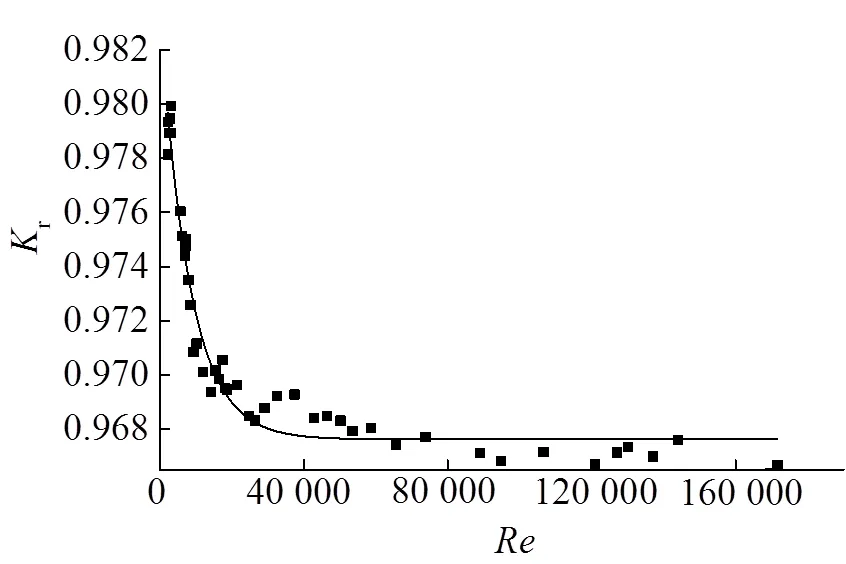
圖11 湍流狀態下與Re關系曲線

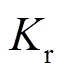
4 結論

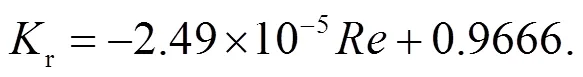
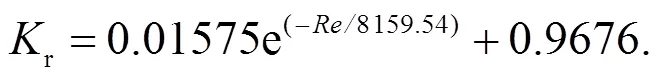
[1] 王雪峰. 基于時差法氣體超聲波流量計的關鍵技術研究[D]. 大連: 大連理工大學, 2011.

[2] 汪曉凌, 黃江濤. 改善超聲波氣體流量計測量精度的方法研究[J]. 輕工科技, 2012, 28(9):124-125.

[3] 唐曉宇, 張宏建, 謝翔, 等. 多聲道超聲波氣體流量計聲平面安裝角度對測量影響的模型仿真和實驗研究[J]. 中南大學學報(自然科學版), 2017, 48(7):1923-1929.

[4] 檀盼龍, 韓思奇. 時差法超聲波流量測量技術研究現狀與應用[J]. 無線互聯科技, 2018, 15(16):31-32.

[5] 杜曉澤, 劉勝祥. 時差法超聲波流量計流量系數影響因素分析[J]. 工業計量, 2019, 29(2):14-15; 38.

[6] 陳浩, 楊鳴. 超聲波流量計雙彎管流場整直問題的研究[J]. 現代科學儀器, 2019(4):5-9.

[7] 孔祥強, 郭璇, 杜廣生, 等. 基于CFD的超聲波氣表結構與流動特性研究[J]. 儀器儀表學報, 2018, 39(9): 220-227.

[8] 孫望, 王魯海, 王兆杰, 等. 基于PIV測量的超聲波流量計內流場特性研究[J]. 實驗力學, 2014, 29(6):695- 702.

[9] 林棋, 陳子鑫, 張義勇, 等. 超聲波流量計概述及流場數值模擬研究[J]. 石油工業技術監督, 2018, 34(11): 43-47.

[10] 賀勝, 彭黎輝, 仲里敏. 基于CFD的超聲波流量計最優聲道位置研究[J]. 儀器儀表學報, 2009, 30(4):852- 856.

[11] 王雪峰, 唐禎安. 超聲波氣體流量計的管道模型仿真和誤差分析[J]. 儀器儀表學報, 2009, 30(12):2612- 2618.

[12] Mousavi S F, Hashemabadi S H, Jamali J. Calculation of geometric flow profile correction factor for ultrasonic flow meter using semi-3D simulation technique[J]. Ultrasonics, 2020, 106:106165.

[13] 鮑敏. 影響氣體超聲波流量計計量精度的主要因素研究[D]. 杭州: 浙江大學, 2004.

[14] 姚平. 復雜流場下氣體超聲波流量計測量精度提升方法[D]. 杭州: 浙江大學, 2018.

[15] 陳煒剛. 氣體超聲波流量計非理想流場分析與補償方法[D]. 杭州: 浙江大學, 2015.

[16] 李躍忠. 多聲道超聲波氣體流量測量關鍵技術研究[D]. 武漢: 華中科技大學, 2010.

Simulation research on Reynolds correction coefficient of rectangular flow channel of ultrasonic gas meter

HE Minghao, YANG Ming*

( Faculty of Electrical Engineering and Computer Science, Ningbo University, Ningbo 315211, China )

In the measurement technology of ultrasonic flowmeter, the research on the Reynolds correction coefficient plays an important role in improving the measurement accuracy. In order to study the relationship between Reynolds correction coefficient and Reynolds number of the gas in rectangular channel under laminar flow condition, the rectangular flow channel is simulated under the condition of small flow at normal temperature and pressure. Based on the analysis of the fitting results, the conclusion is drawn that the Reynolds correction coefficient of the gas in laminar flow in the rectangular flow channel is linearly related to the Reynolds number. By keeping the pressure and volume flow constant, multiple sets of simulation and fitting experiments are carried out at different temperatures. The results show that the linear correlation between the Reynolds correction coefficient and the Reynolds number is still satisfied at different temperatures. On the basis of the above experiments, the relation between the Reynolds correction coefficient and the Reynolds number of the gas in the rectangular flow channel in the turbulent state is studied. Through simulation and fitting by changing the temperature, pressure and volume flow, it is concluded that the Reynolds correction coefficient of the gas in turbulent flow in the rectangular flow channel is nonlinearly related to the Reynolds number.

ultrasonic gas meter; rectangular flow channel; Reynolds number; Reynolds correction coefficient

TH814

A

1001-5132（2021）02-0025-06

2020?08?15.

寧波大學學報（理工版）網址: http://journallg.nbu.edu.cn/

何明昊（1995－）, 男, 湖北武漢人, 在讀碩士研究生, 主要研究方向: 超聲波氣體流量計. E-mail: 651944260@qq.com

楊鳴（1963－）, 男, 浙江寧波人, 研究員, 主要研究方向: 超聲波計量及顯微圖像處理. E-mail: yangming@nbu.edu.cn

（責任編輯 史小麗）