混沌分析和最小二乘支持向量機的畢業生就業率預測模型

翟曉鶴

(新疆醫科大學 護理學院， 新疆 烏魯木齊 830054)

0 引言

隨著高校的擴展，學生人數不斷增加，畢業生的數量隨之增多，大學生就業競爭十分激烈，就業壓力越來越大[1-2]。人們對畢業生就業問題十分關注，同時畢業生就業率是高校學生培養質量的一個重要指標，因此高校對畢業生就業率高度重視，這樣需要對畢業生就業率進行建模與分析，找到影響畢業生就業率的一些主要因素，從而使高校能夠相應的調整學生培養模式，給高校畢業生管理者提供有效的建議，同時為畢業生提供有價值的信息[3]。

對于畢業生就業率預測問題，國內外許多學者都進行了各種嘗試研究，最初為線性建模技術，如：基于ARIMA的畢業生就業率預測模型、基于灰色系統的畢業生就業率預測模型，基于決策樹的畢業生就業率預測模型[4-6]。它們主要針對小規模、變化簡單的畢業生就業率進行預測，當畢業生就業率變化比較復雜時，則就業率預測誤差急劇上升；隨后出現了一些非線性建模技術，如基于機器學習算法的畢業生就業率預測模型，最具有代表性的為人工神經網絡，其具有比較好的非線性建模預測性能，能夠從畢業生就業率歷史數據中挖掘出畢業生就業率變化特點，預測建模效率要優于線性建模技術[7-8]。由于畢業生就業率具有一定的混沌性，而當前機器學習算法進行畢業生就業率預測建模時，忽略了該特點，使得預測結果并未達到最理想的狀態，同時預測精度不太穩定。

以獲得更優的畢業生就業率預測結果為目標，提出了混沌分析和最小二乘支持向量機的畢業生就業率預測模型(Chao-LSSVM)，該模型根據Takers定理對畢業生就業率歷史數據進行混沌分析，采用最小二乘支持向量機擬合畢業生就業率變化特點，為了驗證該預測模型的有效性，與當前經典模型進行對比實驗，驗證了Chao-LSSVM的畢業生就業率預測結果的優越性。

1 混沌分析和最小二乘支持向量機的畢業生就業率預測模型

1.1 混沌分析理論

設畢業生就業率樣本數據集合為{xi}，i=1,2,…,N，N為樣本長度，根據Takers定理[9]，一個混沌畢業生就業率樣本數據可以重構一個具有等價空間的數據，能夠更好地把握畢業生就業率變化規律，等價空間的多維畢業生就業率數據，如式(1)。

X(t)=[x(t),x(t+τ),…,x((m-1)t+τ)]

t=1,2,…,M

(1)

式中，m表示嵌入維；τ表示延遲時間；M表示相空間中的點數，如式(2)。

M=N-(m-1)τ

(2)

從式(2)看出，畢業生就業率歷史數據的混沌分析主要是確定嵌入維、延遲時間，把畢業生就業率歷史數據中把蘊藏的信息充分地挖掘出來，通過相空間重構技術恢復畢業生就業率的混沌特性，本文分別采用飽和關聯維數法確定最優的嵌入維，自相關函數法確定最優的延遲時間。

1.2 最小二乘支持向量機

由于人工神經網絡經常出現一些預測結果偏差比較大的點，即出現所謂的過擬合缺陷，為了改善畢業生就業率預測結果，本文引入最小二乘支持向量機對相空間重構后的畢業生就業率數據進行建模，這是因為最小二乘支持向量機不僅不存在人工神經網絡的過擬合缺陷，建模預測性能十分優異，而且其建模效率更高。對于訓練樣本集合，在支持向量機的基礎上，最小二乘支持向量引入如下的約束條件，如式(3)。

yk[ωTφ(xk)+b]=1-ek

(3)

對如式(3)的問題，最小二乘支持向量機通過下式進行求解,如式(4)、式(5)。

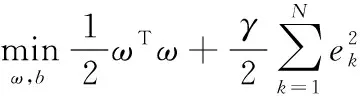
(4)

(5)

式中，γ表示正則化參數[10]。

定義拉格朗日方程，如式(6)。

(6)

式中，αk表示拉格朗日乘子。

根據如下KKT條件，得到αk和b的值，如式(7)—式(10)。

(7)

(8)

(9)

(10)

引入核函數解決非線性回歸問題，即：K(x,xi)=φ(x)Tφ(x)，最小二乘支持向量機回歸的決策形式，如式(11)。

(11)

選擇RBF核函數，如式(12)。

(12)

式中，σ2表示核函數參數。

1.3 混沌分析和最小二乘支持向量機的畢業生就業率預測步驟

(1) 收集若干年的畢業生就業率歷史樣本數據，根據時間先后進行排序，建立一維樣本集合，并對樣本數據做如下歸一化處理,如式(13)。

(13)

(2) 確定一維的畢業生就業率樣本集合的嵌入維和時間延遲，根據嵌入維和時間延遲進行相空間重構，這樣會產生一個多維的畢業生就業率數據，該數據空間變化軌跡與原始畢業生就業率數據變化軌跡相近。

(3) 初始化最小二乘支持向量機的相關參數，如正則化參數，核函數參數。

(4) 采用最小二乘支持向量機對相空間重構后的多維畢業生就業率數據進行學習，并采用10折交叉驗證法確定預測精度最高的最小二乘支持向量機建立畢業生就業率預測模型。

綜合上述可知，混沌分析和最小二乘支持向量機的畢業生就業率預測流程，如圖1所示。

圖1 混沌分析和最小二乘支持向量機的畢業生就業率預測流程

2 仿真測試析

2.1 仿真測試環境設置

為了全面分析混沌分析和最小二乘支持向量機的畢業生就業率預測效果，在相同的仿真測試環境下，選擇當前經典的畢業生就業率預測模型進行對比測試，經典模型具體為：(1) 基于ARIMA的畢業生就業率預測模型(ARIMA)；(2) 灰色系統的畢業生就業率預測模型(GM)；(3) BP神經網絡的畢業生就業率預測模型(BPNN)；(4) 沒有混沌分析的最小二乘支持向量機的畢業生就業率預測模型(LSSVM)。所有模型的測試環境，如表1所示。

表1 所有模型的測試環境設置

2.2 仿真測試的數據

選擇10所學校的畢業生就業率作為實驗對象，每所學校畢業生就業率歷史數據，如表2所示。

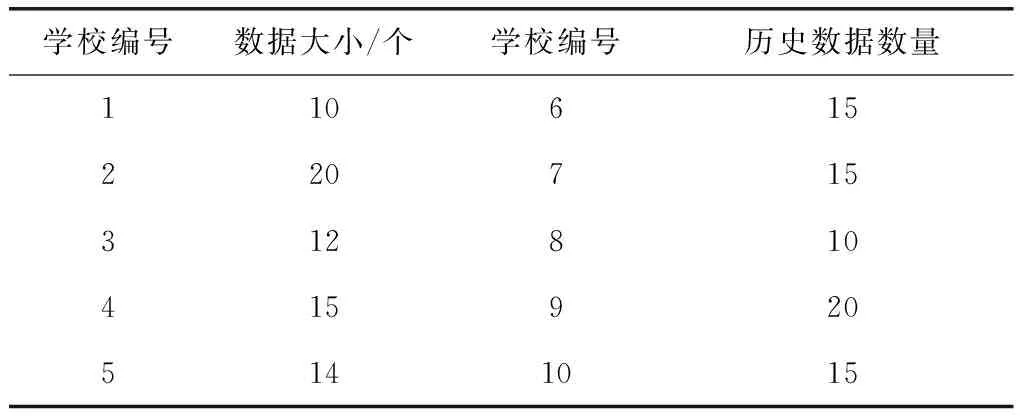
表2 仿真測試的數據

2.3 混沌分析結果

對表2的仿真測試的數據進行混沌分析，確定每一所學校的畢業生就業率數據的嵌入維數和延遲時間，如表3所示。

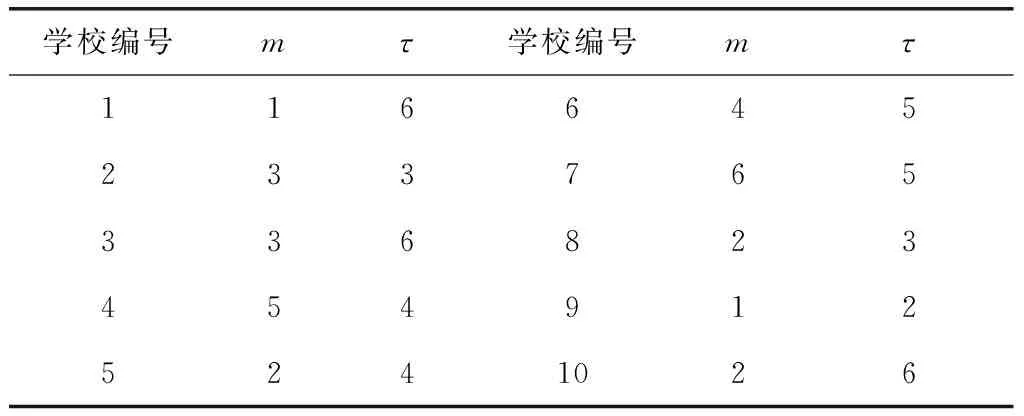
表3 嵌入維和時間延遲的確定

從表3可以看出，不同學校的畢業生就業率數據，它們的混沌特性是不一樣的，得到嵌入維數和延遲時間有一定的差別，根據嵌入維數和延遲時間對表2的畢業生就業率數據進行相空間重構，得到畢業生就業率預測學習樣本集合。

2.4 畢業生就業率預測精度對比

ARIMA、GM、BPNN、LSSVM的畢業生就業率預測精度的平均值，如圖2所示。

圖2 畢業生就業率預測精度對比

對圖2的實驗結果進行對比和分析。

(1) ARIMA、GM的畢業生就業率預測精度低于85%，這是由于ARIMA、GM屬于線性建模技術，只能描述畢業生就業率的線性變化規律，而對隨機性變化規律無法進行有效描述，使得ARIMA、GM的畢業生就業率預測誤差高于15%，超過了畢業生就業率預測的實際應用區間，無法應用于畢業生就業管理中，建模結果沒有什么實際意義。

(2) BPNN、LSSVM的畢業生就業率預測精度要高于ARIMA、GM的畢業生就業率預測精度，因為它們屬于非線性建模技術，可以描述畢業生就業率的隨機性變化規律，但是由于沒有考慮到畢業生就業率的混沌特性，使得畢業生就業率預測精度沒有超過90%，說明BPNN、LSSVM的畢業生就業率結果不理想。

(3) Chao-LSSVM的畢業生就業率預測精度高于ARIMA、GM、BPNN、LSSVM，預測精度平均值超過93%，大幅度減少了畢業生就業率預測誤差，這是因為其結合了混沌分析和最小二乘支持向量機的優點，可以對畢業生就業率變化規律進行精確建模，獲得了理想的預測結果。

2.5 畢業生就業率預測模型的執行效率對比

隨著高校畢業生人數不斷增加，執行效率也成了評價畢業生就業率預測模型的一個重要指標，采用平均建模時間(秒，s)描述畢業生就業率預測模型的執行效率，如圖3所示。

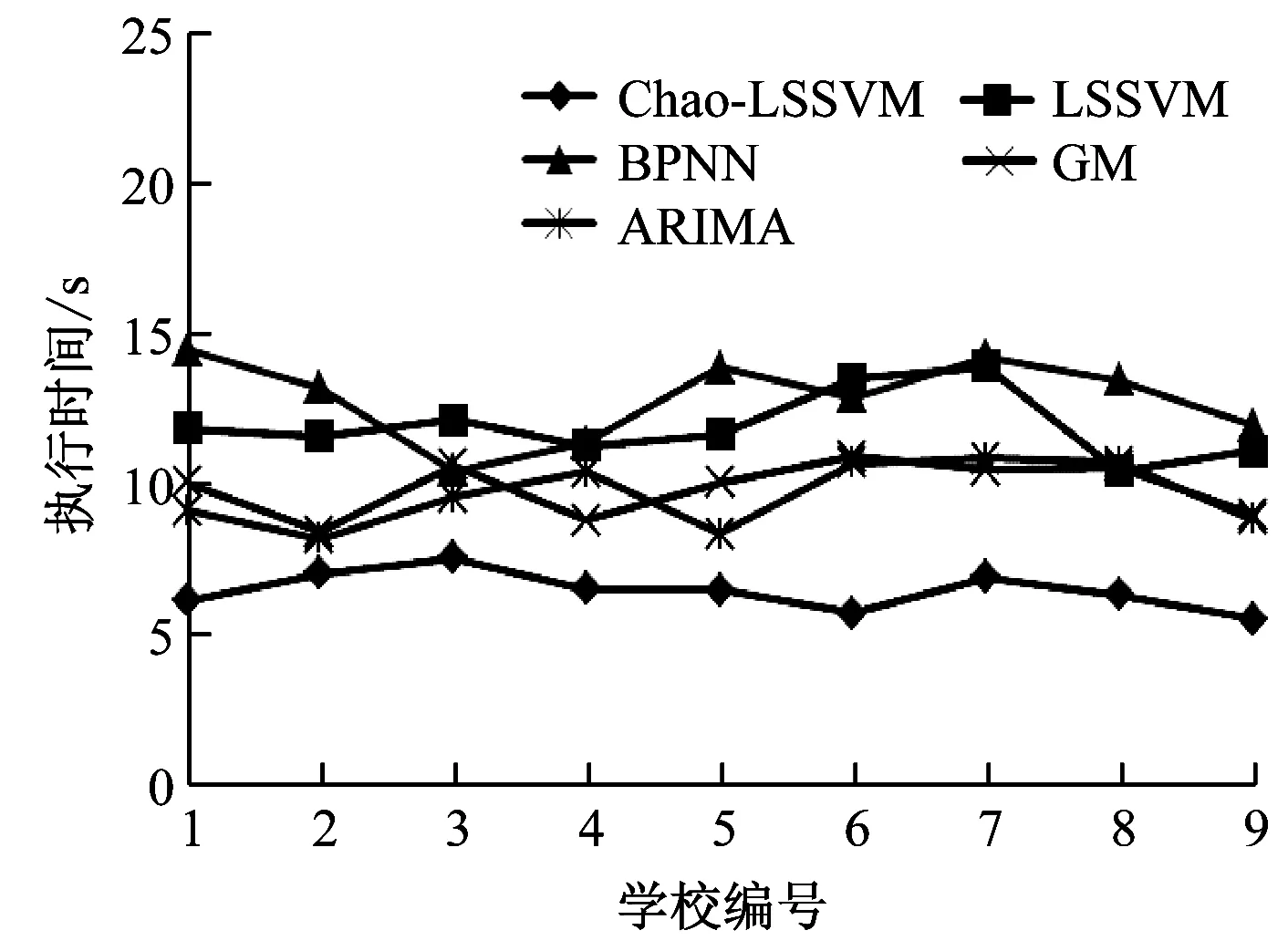
圖3 畢業生就業率預模型的建模時間對比

從圖3的平均建模時間可以知道，Chao-LSSVM的畢業生就業率預測模型的執行時間要明顯少于ARIMA、GM、BPNN、LSSVM的執行時間，這是因為Chao-LSSVM的建模速度更快，提升了畢業生就業率預測建模效率，實際應用價值更高。

3 總結

畢業生就業率預測是當前高校關注的一個重要問題，結合畢業生就業率的變化特點，設計了混沌分析和最小二乘支持向量機的畢業生就業率預測模型，并通過與當前經典畢業生就業率預測模型的對比實驗可以得到如下結論。

(1) 通過引入相空間重構將原始畢業生就業率歷史數據映射到多維空間，更好的挖掘了畢業生就業率歷史數據隱含的變化規律，有助于后續的畢業生就業率預測模型的構建。

(2) 利用最小二乘支持向量機的自適應學習能力，對混沌分析后的畢業生就業率歷史數據進行訓練，可以更好地擬合畢業生就業率變化特點，獲得了較優的畢業生就業率預測結果。

(3) 與經典畢業生就業率預測模型相比，混沌分析和最小二乘支持向量機的畢業生就業率預測精度得到了明顯的改善，同時畢業生就業率預測效率也得到了有效的提升，預測結果可以為高校就業管理人員提供有意義的參考信息。