偏轉角影響磁纖維捕集Fe 基細顆粒的數值模擬

賈中堅,刁永發,張儷安,莊加瑋,沈恒根 (東華大學環境科學與工程學院,上海 201620)

在我國絕大多數工業城市中,大氣污染物主要來源于電力、冶金、化工、建筑建材等重污染企業.其中鋼鐵冶金行業是我國大氣污染的重要來源,其煙塵具有顆粒細、吸附能力強、溫度高、陣發性強等特點[1-3].在鋼鐵冶金行業,機械過濾是較為常見的技術手段,傳統除塵方式存在“穿透窗口”,對于粒徑為0.1～1μm 細顆粒物捕集效率較低[4-5].由于顆粒物粒徑越小,比表面積越大,有毒有害物質往往比大顆粒物呈現更大的活性和毒性,因此細顆粒物對環境和人體健康危害遠高于粗顆粒物[6-7].

纖維作為組成濾料的基本單元,對濾料的過濾效率和壓力損失影響較大.傳統纖維過濾主要依靠慣性效應、攔截效應、擴散效應[8].影響纖維捕集效率的因素很多,隨著斯托克斯數(St)、攔截系數、纖維填充率的增大,捕集效率隨之增大[9-10].近年來研究表明纖維形狀也是影響捕集效率的重要因素[10-13],發現非圓形纖維捕集效率與纖維展玄比成正比[11].通過以上研究發現,傳統纖維對于亞微米級顆粒物的捕集效率較低,無法解決細顆粒物捕集存在“穿透窗口”的問題.

為了提高Fe 基細顆粒的捕集,需要引入外力場,而磁場力作為遠程力在提高微細顆粒捕集方面具有較大優勢.目前關于磁場脫除顆粒物方面的研究主要包括兩個方面,一方面是通過設置外界磁場促進顆粒間團聚,間接實現顆粒的脫除[14-16],研究表明提高增大磁通密度、顆粒質量濃度、停留時間、降低風速有利于提高顆粒去除效率[14];另一方面是通過設置磁性過濾介質直接捕集顆粒[17-20],磁性介質在外界磁場中形成高梯度磁場,其所產生的磁力遠高于只有外界磁場時,因此更加容易實現細顆粒的高效脫除[17].而磁性纖維作為磁性介質的一種,在實現Fe 基細顆粒的捕集方面具有良好效果[21-22].

關于高梯度磁場中磁性介質對顆粒捕集的研究主要包括磁性介質幾何參數以及磁場參數對捕集性能的影響.但磁場方向和顆粒的相對位置決定顆粒間相互作用力[23],而針對不同含塵氣流方向對磁性纖維捕集效率影響的研究較少.由于氣流方向決定了顆粒的慣性作用方向,而高梯度磁場中顆粒運動主要受慣性作用和磁場作用力共同影響,而當含塵氣流方向與背景磁場方向呈不同角度時,會改變Fe 基細顆粒在磁性纖維周圍的運動軌跡,從而產生不同的捕集效率.因此,有必要針對不同偏轉角(含塵氣流方向與背景磁場方向)時磁性纖維捕集Fe 基細顆粒的捕集性能進行研究.本文利用CFD-DPM在傳統纖維上通過用戶自定義函數添加磁場作用力,研究不同偏轉角時纖維捕集性能的動力學行為特征,為進一步提高磁場捕集Fe 基細顆粒提供理論指導.

1 計算模型

1.1 物理模型建立

通過對纖維濾料進行電鏡掃描,可觀察到纖維形貌如圖1.為簡化起見,可選取濾料中局部單纖維作為計算模型,纖維垂直流場方向,顆粒從進口面均勻釋放,流經纖維附近被捕集,如圖2 所示.以纖維中心為圓心,中心到上下邊界的距離為半徑的圓形區域為控制面,纖維填充率定義為纖維面積/控制面的面積,β=,該模型單纖維直徑為20μm,長度設置200μm,高度設置為100μm,經計算可得填充率為4%.

圖1 纖維濾料掃描電鏡圖Fig.1 SEM of fiber filter material

圖2 計算區域與邊界條件Fig.2 Calculation area and boundary conditions

圖3 含塵氣流方向與背景磁場方向夾角示意Fig.3 Schematic diagram of angle between airflow direction and background magnetic field direction

計算區域流場邊界條件設置如下:進口邊界條件為速度入口,出口選取為壓力出口,纖維表面設置為無滑移固體壁面,上下界面設置為對稱邊界.進口和出口處顆粒的邊界條件設置為“escape”,單纖維表面設置為“trap”.模型可簡化為二維,其中背景磁場方向為y方向,垂直背景磁場方向為x方向,規定含塵氣流方向與背景磁場方向所成的夾角(偏轉角)為α,如圖3 所示.磁性纖維在背景磁場作用下產生高梯度磁場,沿背景磁場方向在單纖維前后產生兩個引力區,在兩側形成斥力區,如圖4 所示.

圖4 磁性纖維周圍磁場示意Fig.4 Schematic diagram of magnetic field around magnetic fiber

1.2 流場模型

對通常的纖維過濾情形,濾料內部流動為低雷諾數(Re＜1)流動[24],因此本文采用層流、穩態、不可壓縮模型,其連續性方程和Navier-Stokes 方程如下[25]:

式中: ν 為流體速度, m/s;ρ 為流體密度, kg/m3;μ 為流體動力學黏度, Pa·s;p 為流體壓強, Pa.

1.3 顆粒運動方程

采用拉格朗日法對顆粒進行跟蹤,忽略顆粒間的相互作用,顆粒視為具有相同物性參數的球形粒子,根據牛頓第二定律,單個粒子運動方程[20]如下:

式中: m 為粒子質量, kg;vp為粒子速度, m/s;ρp為粒子密度, kg/m3;Fd為流體對粒子的曳力, N;Fm為磁場中粒子所受的磁力, N;Fb為粒子所受的布朗力,N;Fother為粒子受到的虛擬質量力、壓力梯度力、Basset 力、Magnus 力、Saffman 升力等作用力, N,在本文中忽略這些力.

顆粒在磁場中所受的磁力可以分解為徑向方向(Fmr)和切向方向(Fmθ),表達式如下[22]:

式中:μ0為真空磁導率, 2.256×10-6;χp為顆粒磁化率;H 為背景磁場強度, T;B 為磁性纖維感應磁場強度, T; r 為顆粒中心距離磁性纖維中心的距離, m; θ為顆粒與纖維連線與坐標軸的夾角; df為磁性纖維直徑, m;dp為顆粒直徑, m.

1.4 模型驗證

為了驗證網格數量對計算結果的影響,分別選取3.3 萬、11.7 萬、18.8 萬數量網格對不同St 數下的壓力損失進行計算,如圖5(a).經過計算發現,3.3萬、11.7 萬、18.8 萬所對應的平均壓力損失分別為1.751Pa、1.765Pa、1.767Pa,當網格數為11.7 萬、18.8萬時,兩者計算結果較為接近.從以上分析可以看出當網格數為11.7 萬時,計算結果較為準確,可排除網格數量對計算結果的影響.

單纖維捕集顆粒的捕集效率計算公式如下:

式中: Nin為進口處顆粒數;Nout為出口處顆粒數.

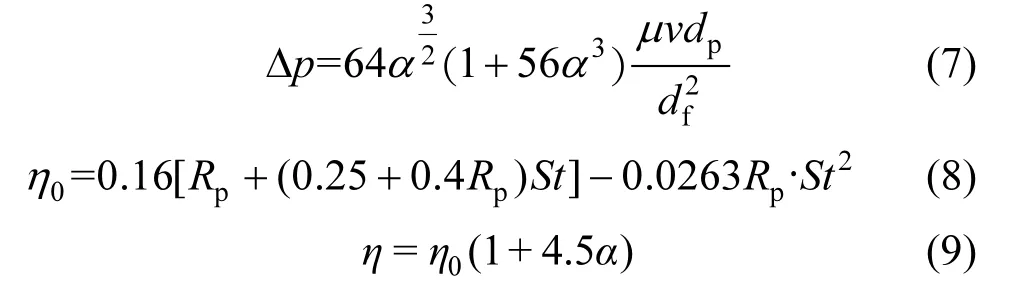
式中: η 為修正后捕集效率; η0為計算捕集效率; Rp為直接碰撞系數Rp=dp?df; St 為斯托克斯數; α 為填充率.

為了驗證單纖維對顆粒捕集模型的準確性,將計算結果與Davies 經驗公式的壓力損失與捕集效率進行對比,如圖5 所示.發現該模擬壓力損失與Davies壓力損失經驗公式(7)結果較為一致,模擬結果與計算結果平均誤差為2.29%,捕集效率計算結果與經驗公式(8)平均相對誤差為3.2%,而與修正后公式(9)計算結果平均相對誤差為14.2%,其中誤差主要是因為Davies 經驗公式只考慮了慣性碰撞與攔截效應,而模擬中考慮了擴散效應,忽略了顆粒間團聚[20,22].為了驗證磁場中顆粒的運動軌跡,模擬結果與Ying 等[26]研究結果進行對比,發現具有很好一致性.為了驗證磁場力作用下的捕集效率,將模擬結果與楊榮清實驗結果[27]對比,發現相對誤差在15%以內.綜上所述,驗證該模型計算結果的準確性與可靠性.

圖5 模型驗證Fig.5 Model validation

1.5 參數設置

模擬中主要的物性參數設置如下:

表1 數值計算采用的常用物理參數Table 1 Common physical parameters used in numerical calculation

2 結果與討論

2.1 顆粒運動軌跡

當偏轉角(含塵氣流方向與背景磁場方向)不同時,Fe 基細顆粒在磁性纖維周圍所受到的力場不同,從而影響顆粒的運動軌跡,為了研究顆粒軌跡與偏轉角的關系,對比分析當偏轉角分別為0°、15°、30°、45°、60°、75°、90°時顆粒運動,如圖6 所示.當角度為0°時,含塵氣流方向正對高梯度磁場中磁性纖維引力區,因此在纖維正對來流風向區域形成捕集區,在背風側形成較大空腔.由于引力區總是正對背景磁場方向,隨著角度的增加,捕集區域也隨之改變,當角度等于60°時,在纖維另一側開始出現捕集區域,當角度達到90°時,在沿氣流方向的纖維兩側出現相等的捕集區域.由于含塵氣流方向決定了慣性作用的方向,而顆粒運動受慣性作用與磁場力共同作用,因此來流風向影響顆粒運動軌跡進而影響顆粒捕集.

圖6 偏轉角對顆粒運動軌跡的影響Fig.6 The influence of the deflection angle on particle trajectory

2.2 磁性纖維捕集效率

2.2.1 顆粒粒徑對不同偏轉角時Fe 基細顆粒捕集效率的影響 如圖7 所示,磁性纖維相對于傳統纖維對不同粒徑Fe 基細顆粒捕集效率的增強作用明顯,尤其是對于較大尺寸的顆粒.當顆粒粒徑較小時,捕集效率

不隨角度的變化而變化,隨著粒徑的增大,捕集效率隨著角度的增大呈現出先減小后增大的趨勢,當角度為60°時捕集效率最低,當角度為0°時捕集效率最高.對于粒徑為2.5μm 的顆粒物,捕集效率受含塵氣流方向影響較為明顯,相對于粒徑較小的顆粒,由于顆粒體積越大所受到的慣性作用越強,而角度的改變直接影響顆粒所受到的慣性作用力,因此較大尺寸顆粒捕集效率易受氣流方向影響.當角度為0°時捕集效率為34.6%,而當角度為60°時捕集效率為25.3%.通過對比不同角度時捕集效率隨粒徑增長的增長速率發現,當角度較小時,捕集效率隨著粒徑增長的增長速率較高,當角度較大時,增長速率較小.

2.2.2 風速對不同偏轉角時Fe 基細顆粒捕集效率的影響 如圖8 所示,隨著風速的增加,捕集效率逐漸減小,減小速率在風速小于0.04m/s 時較大,當風速大于0.04m/s 時減小速率較小.不同風速范圍時對于角度在0°～90°時均存在最低捕集效率,當風速在0.02～0.04m/s 范圍時,最低捕集效率對應角度為45°;當風速在0.06～0.10m/s 范圍時,最低捕集效率對應角度為60°.隨著風速的增加,磁性纖維捕集Fe 基細顆粒受偏轉角影響效果更加明顯,這是因為不同氣流方向時顆粒受到的慣性力方向不同,風速越大,顆粒慣性作用越強,由于顆粒粒徑保持一定,在磁場強度一定的條件下,顆粒受到的磁場作用力不變,此時慣性效應相對磁場作用更加明顯,顆粒運動主要受慣性作用和磁場共同作用影響.

圖7 粒徑對不同偏轉角顆粒捕集效率的影響Fig.7 The effect of particle size on the trapping efficiency of particles in different deflection angles H=0.5T, B=0.05T, v= 0.04m/s

圖8 風速對不同偏轉角時顆粒捕集效率的影響Fig.8 Effect of wind speed on the trapping efficiency of particulate matter in different deflection angles H=0.5T, B=0.05T, dp= 1.0μm

圖9 磁場強度對不同偏轉角時顆粒捕集效率的影響Fig.9 The effect of magnetic field intensity on the trapping efficiency of particles in different deflection angles dp= 1.0μm, v= 0.04m/s

2.2.3 磁場強度對不同偏轉角時Fe 基細顆粒捕集效率的影響 如圖9 所示,隨著背景磁場強度、感應磁場強度的增加,捕集效率逐漸增加,增長速率呈分段增長趨勢.對于角度為0°和60°時,背景磁場強度為0.1～0.3T 范圍時增長速率明顯大于0.3～0.9T 范圍內,而對于角度為30°和90°時,背景磁場強度為0.1～ 0.5T范圍時增長速率明顯大于0.5～0.9T 時的增長速率.這是因為當磁場強度較小時,顆粒所受到的磁場力較小,此時慣性作用和磁場作用共同影響顆粒的捕集效率,增大磁場強度使得磁場所起的作用逐漸增強;當磁場強度較大時,由于慣性作用影響相對較小磁場強度時所起的作用稍有降低,從而造成增長速率減小.捕集效率隨著感應磁場強度增長的變化規律與背景磁場強度的變化規律相似.因為增加感應磁場強度和增加背景磁場強度都將造成磁性纖維周圍磁場作用力增大,雖然慣性作用不變,但對磁性纖維周圍顆粒運動影響較為明顯,磁場作用力的增加,使得更遠處顆粒向磁性纖維周圍運動,而處在磁性纖維周圍的顆粒也更難逃離,從而使得捕集效率增加.

3 結論

3.1 偏轉角(含塵氣流方向與背景磁場方向)影響磁性纖維捕集區域的位置.當角度為0°時,在纖維正對氣流方向區域形成顆粒捕集區,在背風側形成較大空腔.隨著角度的增加,捕集區域也隨之改變,當角度等于60°時,在纖維另一側開始出現捕集區域,當角度達到90°時,在沿氣流方向纖維兩側出現相等的捕集區域.

3.2 當顆粒粒徑較小時,捕集效率不隨偏轉角度的變化而變化,隨著粒徑的增大,捕集效率隨著角度的增大呈現出先減小后增大的趨勢.當角度較小時,捕集效率隨著粒徑增長其增長速率較高,當角度較大時,增長速率較小.

3.3 不同風速范圍時對于偏轉角度在0°～90°時均存在最低捕集效率.當風速在0.02～0.04m/s 范圍時,最低捕集效率對應角度為 45°;當風速在 0.06～0.10m/s 范圍時,最低捕集效率對應角度為60°.

3.4 隨著磁場強度的增加,捕集效率增長速率呈分段增長趨勢.對于偏轉角度為0°和60°時,背景磁場強度為0.1～0.3T 范圍時增長速率明顯大于0.3～0.9T 范圍,而對于角度為30°和90°時, 背景磁場強度為0.1～0.5T范圍時增長速率明顯大于0.5～0.9T 時的增長速率.