考慮儲能電站的清潔能源并網電力系統風險量化與安全效益評估

姜明軍，王文婷

（蘭州理工大學 電氣工程與信息工程學院，蘭州 730050）

0 引言

構建低碳環保、安全高效的新型電網是現代電力系統的基本特征。近年來，隨著清潔能源并網滲透率逐年增加，開發面向清潔能源發展的并網協調控制技術與消納機制成為國內外學者廣泛關注的熱點問題。在我國，受制于地區資源稟賦與設備裝設水平的綜合影響，清潔能源在實際生產、輸出過程中往往難以實現高效、穩定、持續的能量輸出。這種情況下，考慮到儲能設備易于集成、動態響應速度快與能量轉換效率高等一系列優點，研究如何發揮儲能設備對協同促進清潔能源消納的影響，實現源網儲互補控制成為解決該問題的有效途徑。

國內外學者在儲能規劃、儲能調度、儲能效益評價等方面開展了大量研究。文獻［1］兼顧儲能在全壽命周期內的動態投資流影響，提出考慮儲能系統動態全壽命周期特性的多功能應用需求規劃方法；文獻［2］在兼顧系統供電可靠性基礎上，提出面向集群劃分的網源儲多目標兩步規劃方案；文獻［3］從經濟學角度設計了考慮清潔能源隨機性的微電網日前調度與儲能優化調度模型；文獻［4］分析了儲能系統平抑清潔能源并網波動的作用，及由此帶來的削峰填谷效益；文獻［5］從經濟層面綜述了儲能系統在能源互聯網中的重要作用與商業運作模式；文獻［6］聚焦虛擬電廠分布式儲能的靈活調節策略，以提高并網收益為目的構建了優化調度方案；文獻［7］給出了儲能系統在配電系統的專項規劃模型；文獻［8］、文獻［9］給出了儲能技術在電力系統中的實際應用，并據此給出了相應的建模方法。上述文獻對儲能各項研究工作的開展側重技術經濟性方面，較少考慮儲能對降低電網運行風險、提升安全管理與控制等方面的影響。文獻［10］以抽水蓄能電站作為研究對象，給出了面向多風電場與抽水蓄能電站聯合系統的可靠性評估模型與容量可信度模型；文獻［11］給出了儲能提升高比例風電電力系統供電安全的概率評估方法。上述研究一定程度上補充了儲能系統提高清潔能源電力系統供電安全或可靠性的作用與效益評估方法，但是因為清潔能源波動與系統調度是動態校正過程，以靜態概率評估為基礎開展的儲能效益評估研究難以反映電力系統調度行為的動態時序特征。

探討儲能在小時級調度優化過程中，與常規機組協同平抑負荷與可再生能源不確定性，以改善系統調度安全性與系統發電經濟性的效益提升與量化評估問題是本文研究工作的重點。基于該研究框架，本文分析了清潔能源發電不確定性對調度過程經濟性/安全的影響，結合馬爾科夫鏈蒙特卡洛仿真（markov chain monte carlo，MCMC）［12—13］給出完整的效益量化評估方案。本文的主要貢獻包括:分析了儲能對提升電網運行安全的影響，通過量化評估清潔能源電力系統調度運行問題中的運行風險，基于技術經濟性對比，給出相應的效益評估方案，采用馬爾科夫鏈蒙特卡洛仿真實現對電網運行風險的高效求解。應該指出，盡管儲能在控制領域/靈活性評價領域也可以借助其快速充放電特性發揮調頻阻尼控制、或負荷跟蹤功能；但此類功能定位與本文描述研究內容相關度不大，因此暫時不將其納入到本文研究范疇。

綜上分析，本文的主要工作為:① 分析儲能接入對降低電網運行風險的意義；② 給出含儲能清潔能源電力系統的狀態分析模型，并在此基礎上結合馬爾科夫鏈蒙特卡洛仿真給出相應的運行風險量化評估方案；③ 基于對比分析給出儲能對提升電網運行安全的效益評價策略；④ 采用修正IEEE-6節點測試系統驗證所提方案的有效性與先進性。

1 儲能電站對提升電網運行安全必要性

儲能設備包括電化學儲能、熱儲能、抽水蓄能等，是通過在電力需求低谷時儲電，在電力需求高時放電的方式幫助電網更好地融合風電與太陽能發電的一種新技術。儲能增強了電網運行的靈活性，通過協調源-網-荷互補運行，在很大程度上促進了電網對清潔能源的消納與接納能力［6］。作為靈活、可調節的供能方式，儲能電站的全面推廣與科學論證對建設“強支撐、高抗擾、善協同”并網友好型電網具有重要意義。根據實際的應用場景不同，儲能對電網運行安全的影響體現在:

（1）儲能設備可通過其靈活的充放電特性實現能量時移，這對平抑清潔能源發電波動與不同時段的負荷需求具有重要作用。

（2）儲能設備作為外接橋接電能（這里指在外部電能消失或電源切換過程中，由外接設備提供的過渡電源），可通過提供備用容量、負荷跟蹤、系統二次調頻對電網運行發揮作用，這對應對故障狀態的緊急處置問題具有重要意義。

儲能設備的狀態轉移過程如圖1所示。

圖1 儲能設備的狀態轉換過程Fig.1 State transition process of energy storage device

在電力系統負荷低谷期作為負荷從電網汲取電能，在電力系統高峰或者清潔能源波動較劇烈時作為電源作為橋接電源配送至電網。結合儲能工作原理，給出儲能相應數學模型，即

（1）儲能在發電狀態下的上下限約束

（2）儲能在充電狀態下的上下限約束

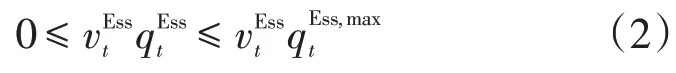
（3）儲能充電電量的上下限約束

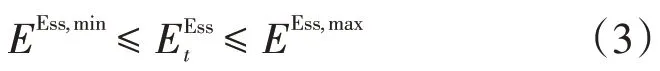
（4）儲能在放電狀態過程中的電量損耗約束

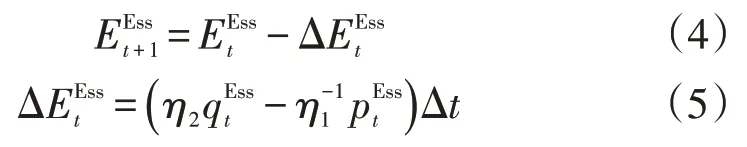
（5）儲能在不同工況下對應狀態耦合約束

2 含儲能的清潔能源并網電力系統狀態分析模型

結合當前得到的系統狀態，進行系統故障狀態分析，求解可能的切負荷情況與發電機組出力調節功率。系統狀態分析模型為

（1）系統有功功率平衡約束

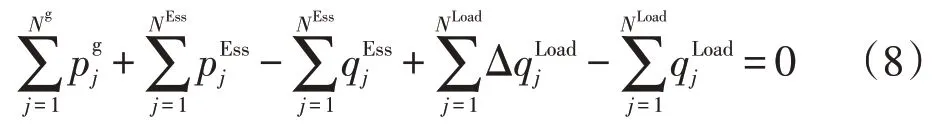
（2）電網在當前狀態下系統潮流安全約束

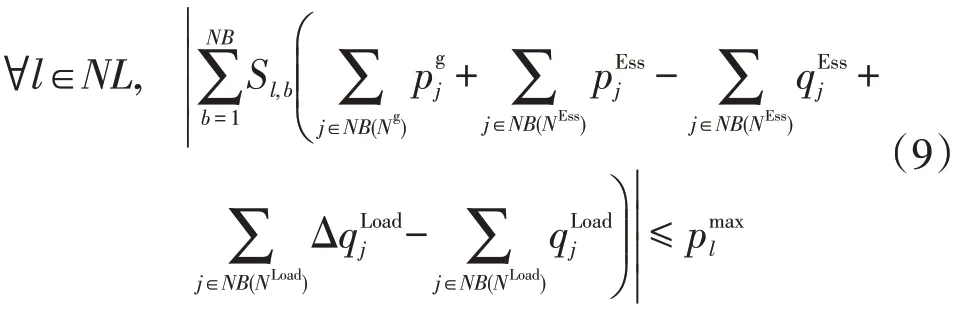
（3）經校正后的發電機出力上下限約束

（4）切負荷功率上下限約束

（5）儲能對應的約束

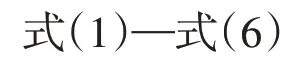
3 基于MCMC的電力系統風險量化評估

儲能設備的加入使電網運行與故障狀態下校正控制過程更為復雜，這增加了系統風險量化評估的難度。常規基于蒙特卡洛仿真開展的風險量化評估基于靜態抽樣原理，較難刻畫系統在復雜條件下故障演變與相關校正策略的影響［7］。據此，本文引入馬爾科夫鏈蒙特卡洛仿真研究儲能在清潔能源電力系統風險量化評估中的作用與影響。

MCMC是一種基于非常見概率分布的特殊抽樣策略［8］，其基本原理是:結合拒絕—接受的采樣思想，通過對通用概率分布進行采樣生成馬爾科夫序列，并使其平穩分布逼近到待研究的非常見概率分布。與常規蒙特卡洛仿真（monte carlo，MC）相比較，MCMC不僅可以實現對未知概率分布或動態隨進型概率分布的有效模擬，對高維多元概率分布函數也具有較好的采樣效率。

設隨機過程{xt,t∈T}初始狀態為x0；T為單位時間間隔t的集合；I為滿足馬爾科夫隨機過程的系統狀態的集合；f(xt)為xt所對應的概率密度分布函數，針對任意時刻的系統狀態xt滿足應無后效性條件:

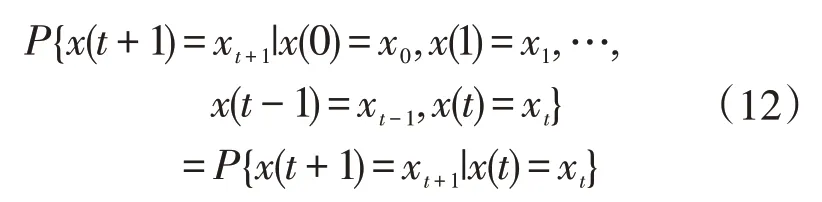
式中:{xt,t∈T}為馬爾科夫鏈，根據柯爾莫哥洛夫定理可得:當t→∞時，xt與初始狀態無關，其對應的狀態密度分布即為穩態概率分布。由于采樣所得到的馬爾科夫鏈在尚未達到收斂時，其概率密度分布并不等于穩態分布。因此評估前，需要去掉前m個采樣序 列（ 燃 燒 期 ），并 將 剩 余 采 樣 值{xj,j=m+1,m+2,…,n}作為滿足該未知概率密度分布函數f(x)對應的采樣值。此時f(x)的期望為

式（13）表示遍歷平均，遍歷定理保證了對任何一個固定的m，在t→∞時E(f(x))會逐漸趨近于f(x)的期望值，而該期望值是在x的穩態分布為f(x)的條件下得到的。

MCMC是在Metropolis-Hastings（M-H）采樣框架下，利用建議分布產生一個潛在的轉移點，并通過接受—拒絕方法決定是否轉移至該樣本點。不同的轉移（由建議分布決定）與構造（由接受分布決定）對應不同的MCMC 方法。以下采用Gibbs 采樣器給出故障狀態的采樣與分析流程［10］。

步驟1:初始化系統狀態，假設第k個系統狀態為xk={x1,k,x2,k,...,xj,k,…,xL,k}，對k+1 個系統狀態進行MCMC采樣。

步驟2:依次對系統各元件的故障/運行狀態進行隨機采樣:設第j次迭代得到的系統采樣狀態是{x1,k+1,…,xj-1,k+1,xj,k,…,xL,k} 。 其 中 ，{x1,k+1,…,xj-1,k+1}是第j-1 次迭代得到的元件采樣狀態；{xj,k,…,xL,k}是待更新的系統元件狀態。采用逆抽樣原理，隨機產生一個服從均勻分布U（0，1）的隨機數u，該元件發生故障的條件概率為

其中p′、p″的具體表達式為

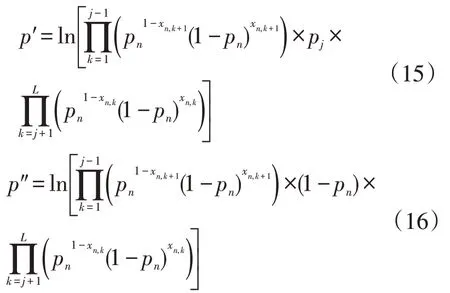
第j個元件的運行狀態判據為

如此循環迭代L次，即可得到當前系統元件的具體狀態。

步驟3:隨機生成一個服從均勻分布U（0，1）的隨機數，采用逆抽樣原理［10］求取系統狀態的狀態持續時間。

步驟4:代入狀態分析式（7）—（11），統計當前狀態切負荷情況，如產生切負荷，將其累加統計到相應的可靠性評價指標中來。所采用的可靠性指標包括:

期望缺供電量（expected energy not supplied，EENS）:即系統在給定時間區間內因發電容量短缺或電網約束造成負荷削減的期望損失電量，為

失負荷概率（lost of load probability，LOLP）:即電力系統在給定時間區間內因供求不匹配造成負荷削減的期望失負荷概率，為

缺電頻次（lost of load frequency，LOLF）:即電力系統在給定時間區間內因供求不匹配造成負荷削減的期望失負荷頻率，為

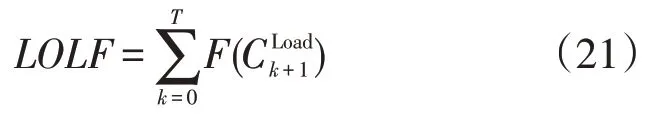
步驟5:檢驗步驟4形成的風險指標是否達到收斂預期，如果達到收斂條件，退出計算過程并輸出計算結果，否則轉步驟2。所采用的收斂性條件為

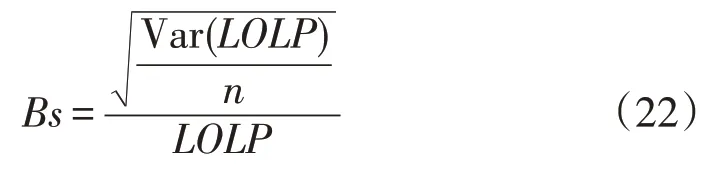
4 基于風險評估的儲能安全效益分析

為量化儲能對提升電網運行安全的影響，這里基于MCMC 風險量化評估，通過計算儲能并網前后電力系統對應的期望停電損失（具體體現在EENS指標），以及不同的對比方案下的電力系統旋轉備用情況，通過對比分析即可得到儲能電站對電網風險效益的整體改善情況。

不妨設儲能并網前后，電力系統風險評估結果依次是EENSbefore與EENSafter，此時儲能并網產生的增量安全效益為

式中:Y為切負荷懲罰系數，本文取值為30元/kWh。

儲能設備對提升電網安全效益的計算流程如圖2所示。

圖2 基于MCMC的電力系統風險評估流程Fig.2 Risk assessment process of power system based on MCMC

5 算例分析

以IEEE RTS 6-bus測試系統為例對所提模型進行有效性測試，該測試系統的具體網架拓撲結構單線圖如圖3所示。為反映清潔能源并網問題對電力系統長期運行風險的影響，根據文獻［10］，假定風電機組安裝在5 號母線上，裝機容量為50 MW。隨機抽取若干風電場景，并通過場景削減技術［11］篩選典型場景，圖4 給出了本文所采用的典型風電場景。在此基礎上，將儲能裝設在節點1上，分別在所得到的不同風電場景下開展電力系統運行風險評估，并將不同場景下得到的運行可靠性評估指標結果的期望值作為最終的評估結果。此處各可再生能源發電場景下開展的MCMC抽樣收斂系數均設置為0.5%。

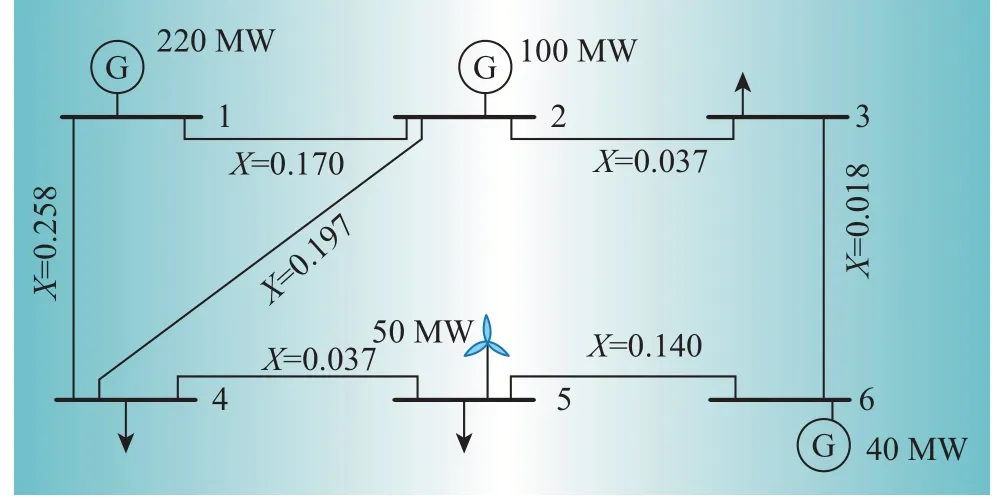
圖3 測試系統的網架結構Fig.3 Grid structure of test system

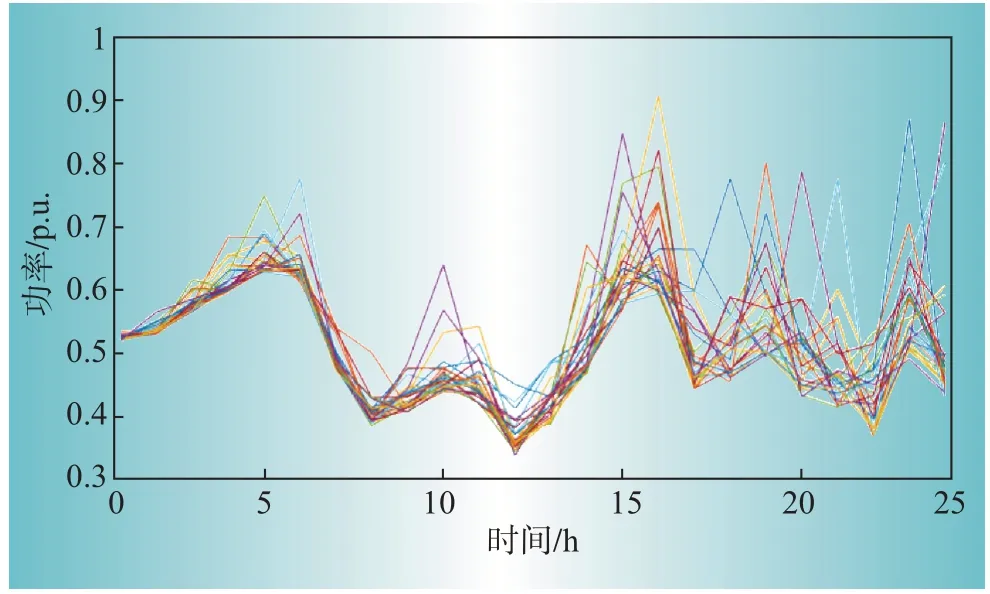
圖4 典型風電場景Fig.4 Typical scenarios of wind power

儲能投入前后電力系統運行可靠性結果的差異如表1所示。方案1為不考慮儲能接入的電力系統運行風險評估方案；方案2 為考慮儲能接入的電力系統運行風險評估方案。

由表1 可知，儲能并網后電網各類運行風險指標呈現不同程度的降低，這揭示了儲能對電網運行風險帶來的效益。其中LOLP指標較對比方案下降了9.01%；LOLF 指標較對比方案下降8.11%；EENS指標較對比方案下降了11.50%。代入式（23），由此可知儲能并網產生的增量安全效益為（1.322 0-1.305 5）×102×30=49.50 萬元/年，這顯示了將儲能裝設在電網以改善供電安全的優勢。并進一步說明，儲能電站并網對其運行方式改善最大的是電量效益，即通過靈活調節運行工況實現削峰填谷，從而避免系統切負荷情況的發生。

表1 不同方案的風險評估結果Table 1 Risk assessment results for different approaches

在此基礎上，為對比本文所提方案在儲能效益分析中的有效性，本文將方差系數設置為0.05，并對比了常規蒙特卡洛仿真與MCMC 進行風險評估的結果如表2所示。

表2 不同評估方案的計算效率對比Table 2 Comparison of calculation efficiency of different evaluation schemes

由表2 可知，與常規MC 相比較，本文所提方案計算時間縮短了40.62%。這也說明:在相同收斂系數條件下，本文方法具有更好的采樣效率，從而具備更優越的計算性能。

此外，為系統闡述儲能安裝布局對系統運行安全的影響，制作對比案例。方案2:將儲能裝設在母線5；方案3:將儲能裝設在母線1；方案4:將儲能裝設在母線6。在此基礎上對含儲能設備的清潔能源電力系統進行MCMC 風險評估，從而得到結果如表3所示。

由表3 可知，儲能裝設地點不同對電力運行的影響也各不相同。與將儲能分別裝設在電源側相比較（方案3 與方案4），儲能靠近負荷側（方案2），其對保障電力安全供電的能力相對越強。相應地，運行風險評估指標越小。究其原因在于，節點5 屬于獨立負荷節點，線路4 與線路5 任意一條停運均會導致負荷脫扣。將儲能裝設在該節點顯然能一定程度提高負荷被迫脫扣的概率與嚴重度。

表3 不同儲能裝設位置的電網風險評估指標Table 3 Grid risk assessment indicators for different ESS installation locations

6 結束語

本文以儲能對提升電力系統安全效益作為研究背景，結合馬爾科夫鏈蒙特卡洛仿真提出一套嶄新的電力系統運行風險評估方案。該方法考慮了儲能設備對電力系統短期運行的影響以及儲能電站工況轉換實際物理約束，通過建立精確有效的儲能單體數學模型及其狀態分析模型，實現了電力系統運行風險的精細化評價。最后以修正的IEEE-6 節點測試系統為例，論證了所提模型的有效性。該方法為短期時間尺度下研究儲能對提升電網安全及其效益評價提供了新思路。