細繩牽引條件下二體彈性碰撞的分析與討論

張 孟 陸 慧 吳趙龍 鐘菊花

(1 華東理工大學物理系,上海,200237)

碰撞是物質間作用的常見形式,表現為兩粒子或物體間極短時間的相互作用,碰撞過程中伴隨著動量、能量和角動量的轉化和轉移。因其涉及物理學中諸多的守恒定律,故碰撞知識點是高中和大學物理的重要內容。現有的物理學教材和文獻對兩小球的非牽引碰撞做了非常詳盡的討論[1-7],但對于細繩牽引條件下的碰撞卻鮮有文獻報道。文獻[3]以高中物理教學常用的速度關聯方法對理想剛性細繩繃直條件下的兩球碰撞問題展開了多種解法的討論,而文獻[4]從能量角度定性討論了牽引碰撞問題,但對牽引過程的動力學方程和兩物體運動狀態隨時間的演化過程沒有給出具體的定量分析。為深入研究牽引碰撞的本質規律,本文對兩小球更為一般的彈性牽引碰撞進行分析與討論,細繩牽引下碰撞過程模型如下:

如圖1所示,光滑平面上用長為x0的輕質細繩連接質量分別為m1與m2的小球,初始時細繩松弛,m1速度大小為v0,m2靜止,細繩拉緊以后,兩小球運動狀態的變化類似碰撞過程,故稱為牽引碰撞。

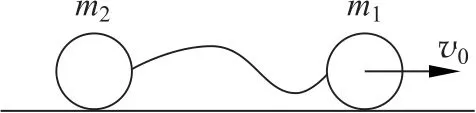
圖1 牽引碰撞示意圖

當小球和細繩均完全無彈性時,兩小球發生完全非彈性牽引碰撞,碰撞后兩小球以相同速度繼續運動[4]。然而,一般情況下小球和細繩均具有一定彈性,以下將建立諧振子模型對彈性牽引碰撞的性質進行研究。

1 模型建立

為了描述牽引碰撞過程中小球和細繩的彈性形變,首先建立簡諧振子模型代替系統中的彈性部分。該模型清晰直觀,簡化了彈性牽引碰撞的具體過程,盡管忽略了細繩的松弛狀態,但仍可以將牽引碰撞的性質闡述清楚。

如圖2所示,該諧振子模型將兩小球發生彈性牽引碰撞時未形變的部分看成質量分別為m1與m2的剛性物體,而形變部分質量很小,可看作輕質彈簧(原長為x0),并假設回復力F與形變位移x-x0成正比,又因為碰撞過程通常存在能量耗散,設耗散力f與形變速度˙x成正比[2],即

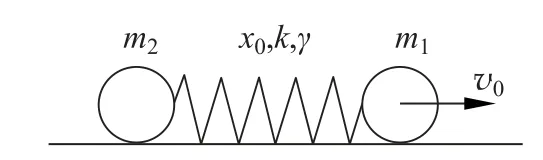
圖2 彈性牽引碰撞的諧振子模型

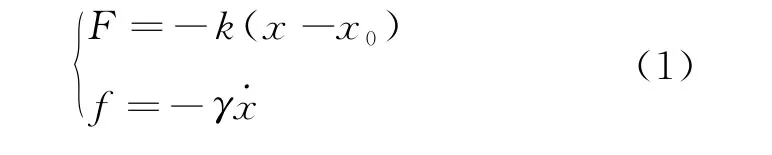
特別地,若兩小球發生完全彈性牽引碰撞,則彈簧振子形變過程中不存在能量的耗散,即γ=0,耗散力為零。除此之外,在非完全彈性牽引碰撞中,γ均不為零,且γ越大表示牽引碰撞中能量耗散越快。阻尼存在時彈性牽引碰撞的阻尼力如圖3所示。

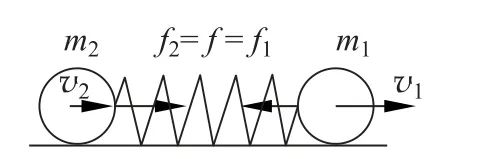
圖3 阻尼存在時彈性牽引碰撞的示意圖

為方便分析,進一步假設該模型的初始狀態為:物體m1以v0速度運動,m2靜止,且彈簧處于原長x0。以下在該模型的基礎上對完全彈性牽引碰撞與非完全彈性牽引碰撞進行分析討論,且考慮到最終要分析實驗室系中的觀察結果,故為避免參照系變換引入的麻煩,以下分析直接在實驗室系進行計算。

2 完全彈性牽引碰撞

對于兩小球的完全彈性牽引碰撞,設x1與x2分別為物體m1與m2的位置,則根據動量守恒定理與動力學方程,有

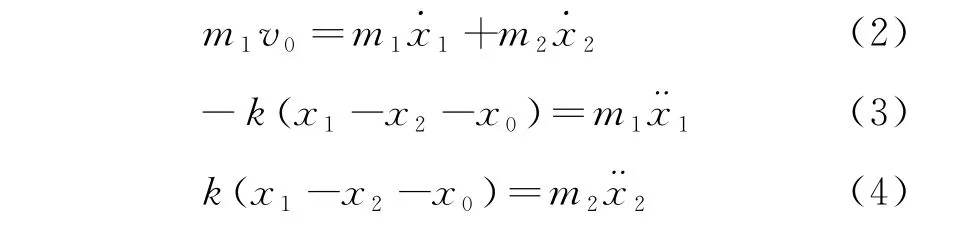
分別對式(3)與式(4)求導,并與式(2)聯立,可得

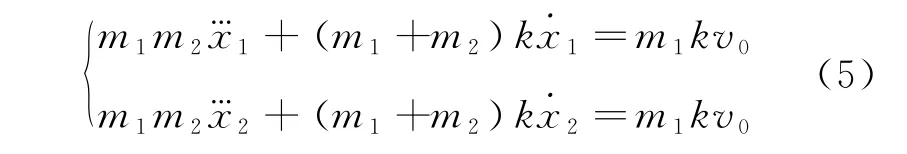
為求解式(5)的三階常系數非齊次微分方程,列出其初始條件

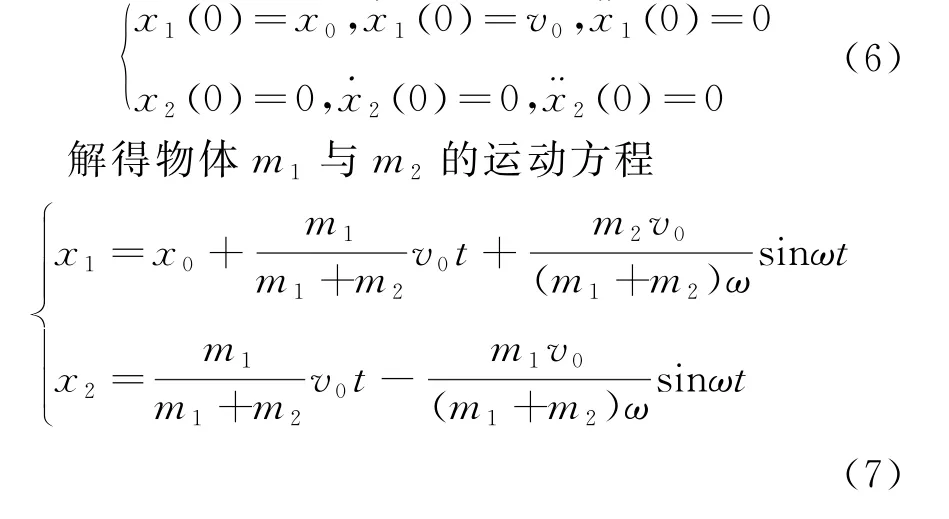
進一步計算可以得到兩物體的速度大小v1與v2以及彈簧長度x隨時間的變化關系

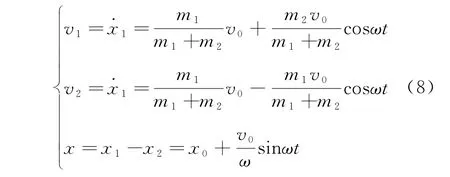
采用MATLAB對上述解析式進行數值計算和分析,給出兩小球的速度v隨時間t演化的曲線圖,其中m1=1.5kg,m2=1kg,x0=1m,v0=1m/s,k=0.6N/m。

分析式(8)并對照圖4可知,在完全彈性牽引碰撞中,兩小球的速度隨時間發生周期性變化,且諧振子的振動永不停止。速度表達式中的常數項等于質心速度,振蕩項符號相反,即動量在兩小球之間不斷地發生周期性交換;做伽利略變換后,質心系中兩物體反相位振動,因而彈簧長度以相同頻率周期變化,即能量在動能與彈性勢能之間不斷轉化。同時,系統的總動量守恒,總動能在諧振子恢復原長時守恒,滿足完全彈性牽引碰撞的要求。

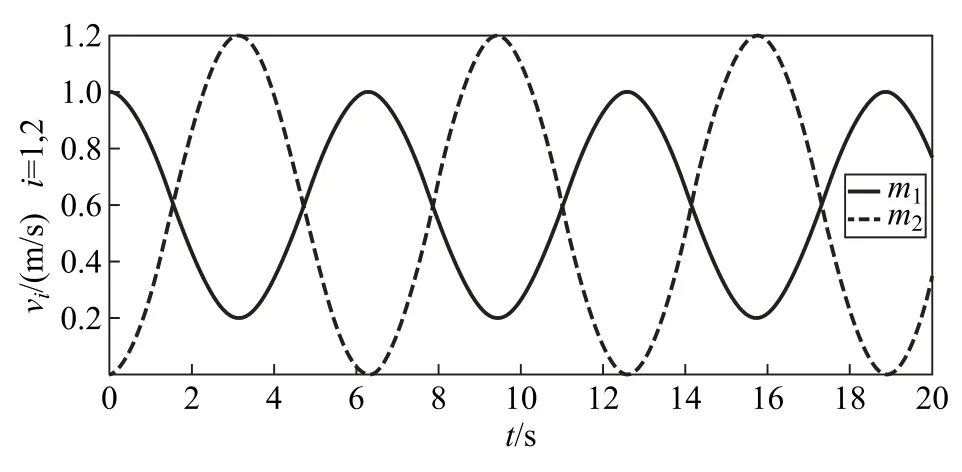
圖4 完全彈性牽引碰撞后兩物體的v-t圖

特別地,當小球和細繩完全失去彈性時,即k→∞,ω→∞,則運動方程化為

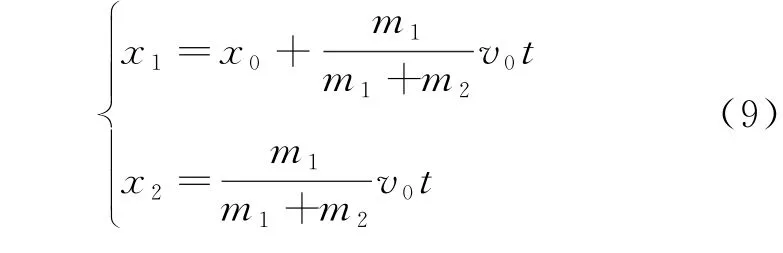
即兩小球以相同速度繼續運動,類似完全非彈性牽引碰撞。

3 非完全彈性牽引碰撞

對于非完全彈性牽引碰撞,γ≠0,則動力學方程式(3)與式(4)應修正為

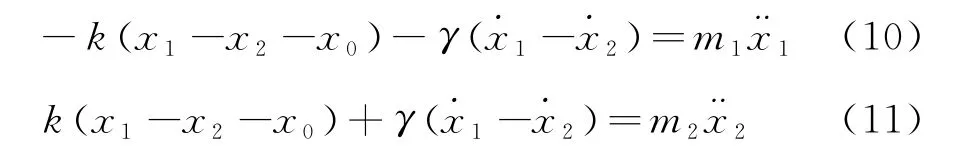
對式(2)求導可得

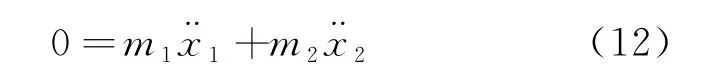
分別對式(10)與式(11)求導,并與式(2)、式(12)聯立,可得三階常系數非齊次微分方程

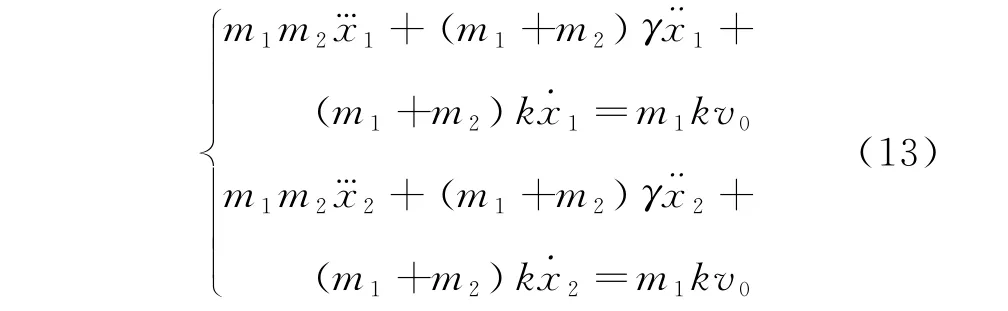
同時,初始條件修正為

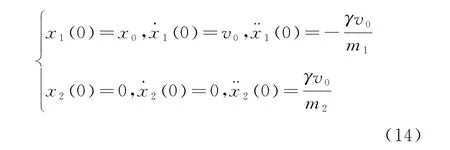
進一步計算可得

②β=ω時,解得

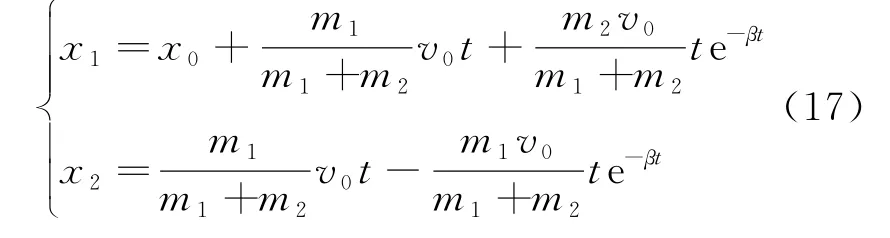
進一步計算可得

進一步計算可得

分析式(20)可知,當形變過程耗散較慢時,兩物體相對速度大小與彈簧長度衰減振蕩,經過更長時間后振蕩項才衰減為零,最終兩物體仍以相同速度運動,彈簧恢復原長。

圖5和圖6分別給出了非完全彈性牽引碰撞(β＞ω,β=ω和β＜ω)時兩物體m1和m2的運動狀態v-t圖。其中m1=1.5kg,m2=1kg,x0=1m,v0=1m/s,k=0.096N/m,γ分別為:0.83N·s/m(β＞ω),0.48N ·s/m (β=ω),0.13N·s/m(β＜ω)。

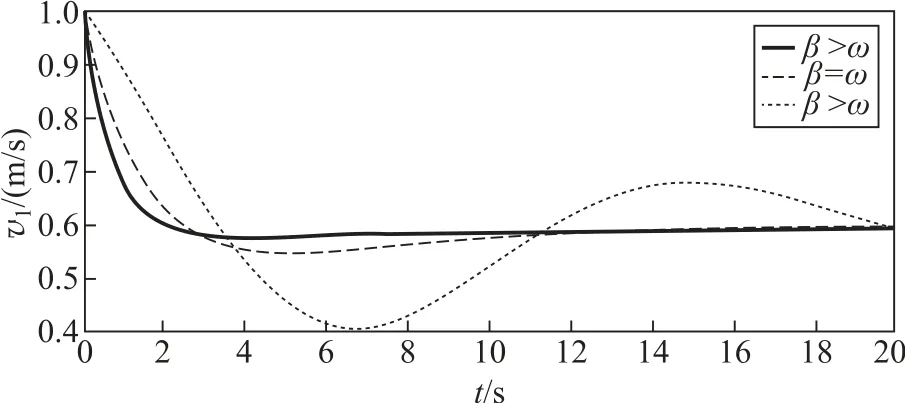
圖5 非完全彈性牽引碰撞后物體m1的v1-t圖

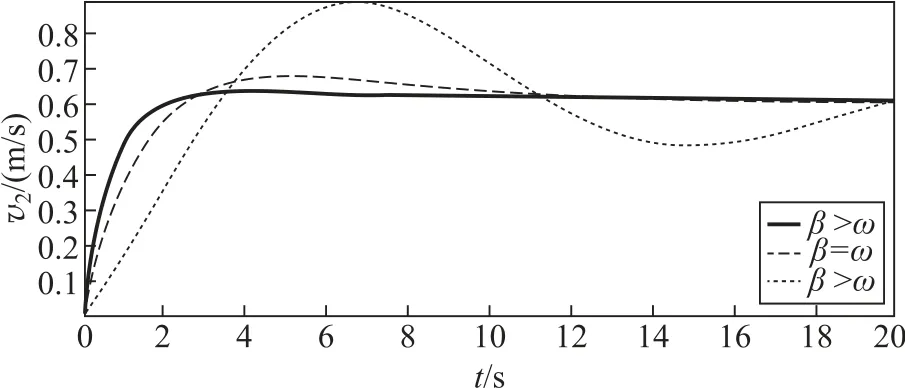
圖6 非完全彈性牽引碰撞后物體m2的v2-t圖

將圖5和圖6與式(16)、式(18)、式(20)對照可知,當形變過程耗散較快時,兩物體相對速度大小與彈簧長度單調衰減,且β＞ω時較β=ω的情況衰減得更快;當形變過程耗散較慢時(β＜ω),兩物體相對速度大小與彈簧長度振蕩衰減。經過長時間后兩物體均以相同速度運動,彈簧長度也均恢復原長。

需要指出的是,由于細繩只有伸長時才會有收縮張力,壓縮時細繩變軟,不會有拉伸的張力,所以嚴格地說,本文采取的彈簧振子模型,與細繩模型還是存在差異的。但從上面討論的結果來看,細繩模型在完全彈性牽引碰撞時兩小球也做能量不損耗的周期運動,只是每個周期內前半段與后半段運動不對稱,一段受到回復力,另一段細繩變軟不受力,兩小球會發生碰撞,作用效果類似向外的回復力;非完全彈性牽引碰撞時,阻尼力僅在細繩拉伸時存在,壓縮時同樣不受力,運動形式也與彈簧振子模型非常相似。因此,在彈簧振子模型基礎上,本文對細繩牽引條件下兩體碰撞做了有益的討論和研究。

此外,如果在質心系中考慮該問題,可以將二體問題轉化為單體問題。以質心為原點,兩小球的位置分別為與,以完全彈性情況為例,物體m1在質心系中的折合質量為,列出其相對于物體m2的動力學方程

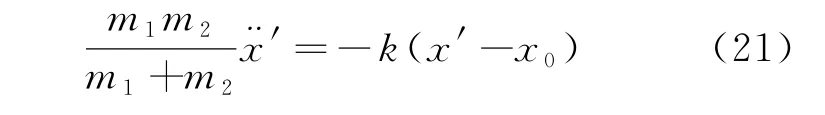
由此可以解得相對位移與相對速度

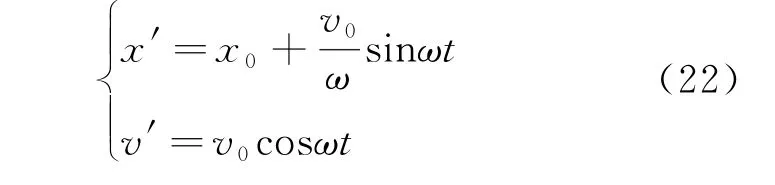
兩質點相對質心系的速度為

因為最終需要求解實驗室系中兩小球的運動,故需要根據以下方程組進行變換

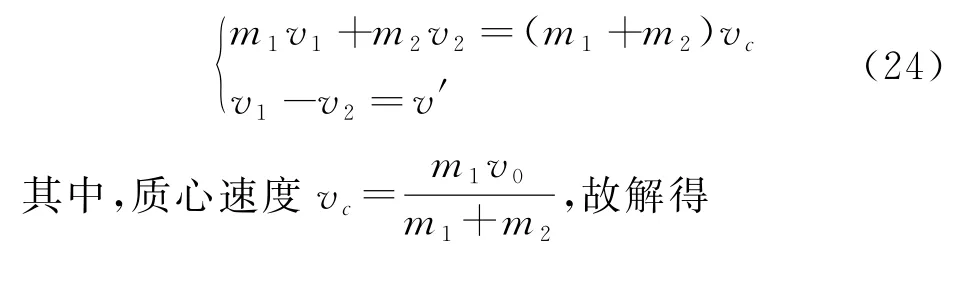
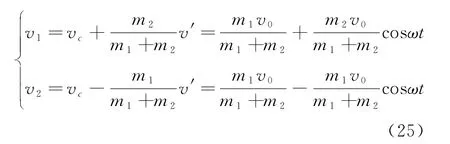
該結果與上文中在實驗室系的結論式(8)相一致。因此,如果讀者對折合質量與參照系變換較熟悉,則在質心系中計算可以相應減少數學運算的復雜度。

4 結語

通過對牽引碰撞采用諧振子模型的分析與討論,可以得到彈性牽引碰撞的具體動力學表達式和各種性質:

①兩小球發生完全彈性牽引碰撞后,總動量與總能量均不損失,且諧振子恢復原長時動能守恒。式(8)與式(9)表明,兩小球的相對速度與諧振子長度發生周期性變化,永不停止。

②兩小球發生非完全彈性牽引碰撞后,總動量不損失,但總能量減小。式(16)、式(18)與式(20)表明,當耗散力較大時,兩小球相對速度與諧振子長度不斷衰減,當耗散力較小時,兩小球相對速度與諧振子長度衰減振蕩,且最終均趨于相同的運動狀態:兩小球以相同速度運動,彈簧恢復原長。

一般情況下,碰撞總伴隨能量損失,因而非完全彈性牽引碰撞更符合實際情況。與完全非彈性牽引碰撞類似,非完全彈性牽引碰撞后兩小球以非線性變化方式也趨于以相同速度運動,故文獻[1]～文獻[4]中相關的習題解答是合理的。