對等溫條件下理想氣體伯努利方程的討論
周 越 張國鋒
(1 北京林業大學理學院,北京 100083;2北京航空航天大學物理科學與核能工程學院,北京 100191)
1 問題的提出
在普通物理教材中,對伯努利方程的討論一般僅限于理想流體的情況,即假定流體無粘性且不可壓縮。與液體相比,氣體的可壓縮性要大得多,密度可以發生顯著的變化,在流速遠低于聲速的條件下才能近似地將其視為理想流體[1]。要精確地定量分析氣體的狀態參量和流速的關系,應考慮密度變化的影響。在氣體動力學中,一般把氣體的流動視為等熵過程,即忽略氣體和外界的熱交換[2]。如果氣體與熱庫良好地接觸,膨脹和壓縮過程又進行得足夠緩慢,則氣體的溫度近似保持恒定,這時可以按等溫過程處理。
在《等溫條件下可壓縮理想氣體的伯努利方程》一文(以下簡稱《等》文)中基于能量守恒推導了等溫條件下理想氣體的伯努利方程[3],得到
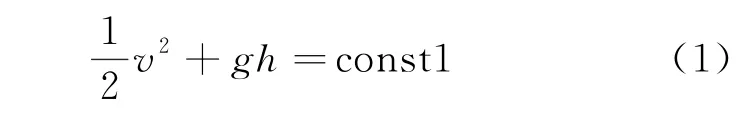
然而,式(1)的正確性是值得商榷的。理由如下:考慮理想氣體在截面漸變的水平管道內做準一維定常流動,如式(1)成立則管道內氣體的流速v將保持恒定。由質量流量守恒ρSv=const2可知,在v不變時氣體密度與管道截面積成反比;在等溫過程中,氣體的壓強又與密度成正比,顯然管道內氣體壓強的縱向分布是不均勻的。設想在管道內取一個同軸的柱體,由于柱體兩側壓強不同,柱體內的氣體必然存在加速運動,這與流速v恒定矛盾。
2 問題分析
如圖1,考慮做定常流動的理想氣體中的一個截面變化的流管,流管兩側的氣體壓強、密度、速度和截面面積為p i、ρi、v i和S i(i=1,2)。假設經過微小時間間隔Δt后a1a2之間的氣體運動到b1b2處。由定常流動的性質可知b1a2之間的氣體狀態沒有任何變化,氣體亦不可能從流管側面逸出,因此a1b1之間的體積元ΔV1和a2b2之間的體積元ΔV2中的氣體具有相同的質量Δm,在計算能量變化時只需考慮體積元ΔV1和ΔV2的能量差。《等》文中認為根據能量守恒定律,外力做功應等于ΔV1和ΔV2中氣體的機械能和內能增量,即
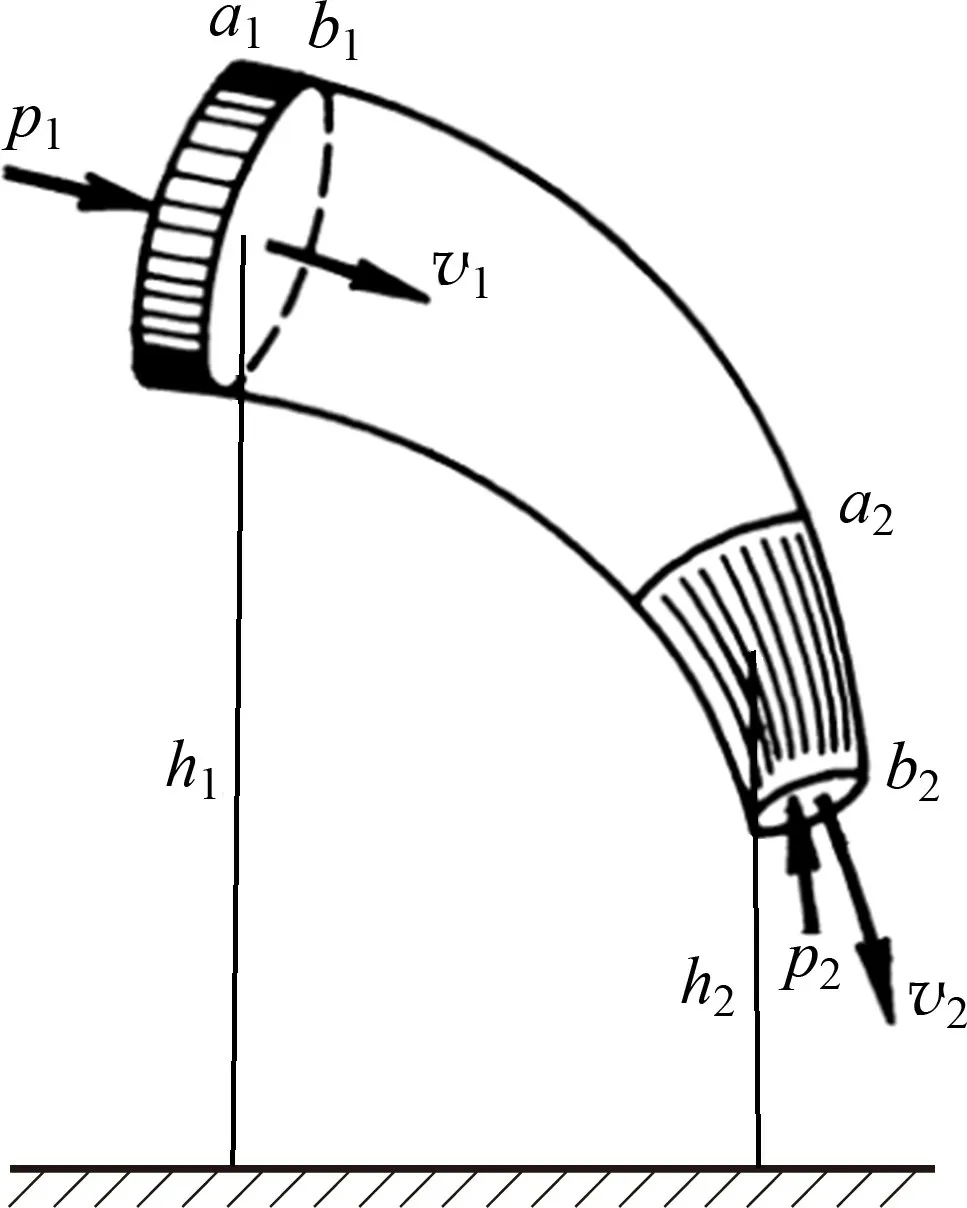
圖1 定常流動的理想氣體截面變化
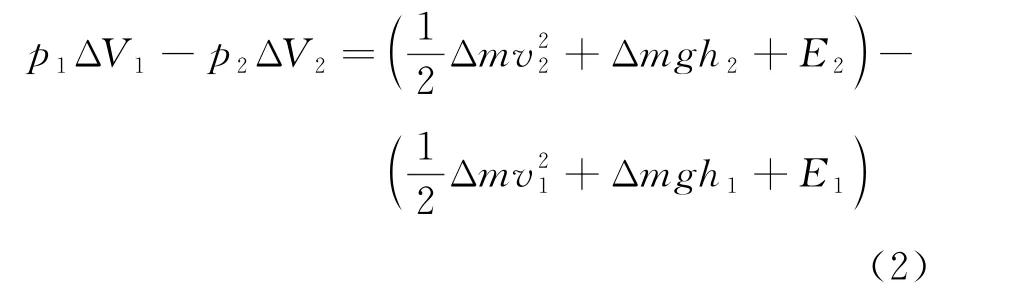
但式(2)存在兩個問題:首先,理想氣體的內能E是溫度T的單值函數,對于等溫過程,氣體的內能恒定,并不存在增量;尤其重要的是,在等溫過程中氣體與外界存在熱交換,利用能量守恒列出等量關系式時,必須將傳遞的熱量Q考慮在內,在式(2)中因遺漏這一項而導致了錯誤的結果。
3 方程的推導
下面重新推導等溫條件下理想氣體伯努利方程的表達式。如前所述,在等溫過程中理想氣體的內能不變,由能量守恒,外力做功加上流動過程中氣體吸收的熱量應等于氣體機械能的增量
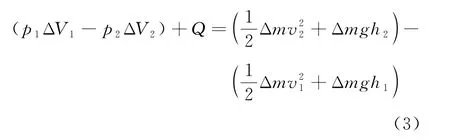
由波義耳定律p V=const3可知
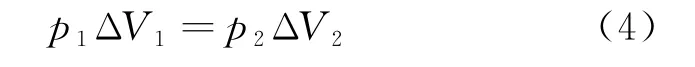
利用式(4)可將等溫過程中氣體吸收的熱量表示為
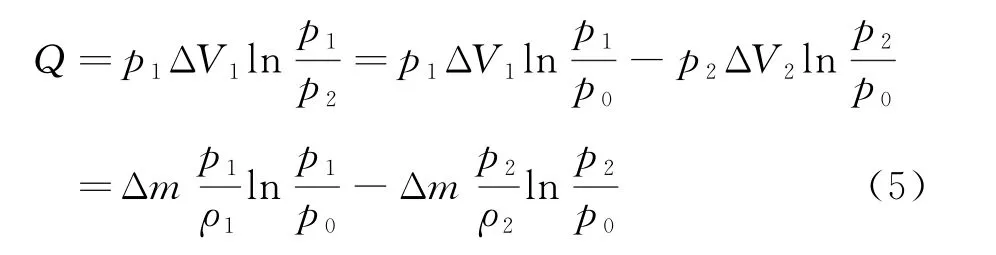
其中p0為任意常壓強。將式(4)和式(5)代入式(3)并將下標相同的項移到等號同側,可得
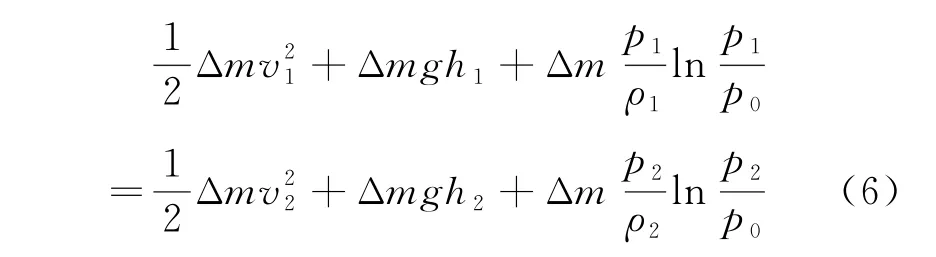
兩邊同時除以Δm,得
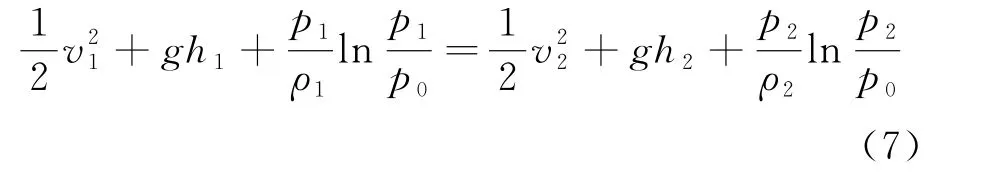
由于流管內兩個截面的位置是任意的,等號兩側應共同等于一個常量,即
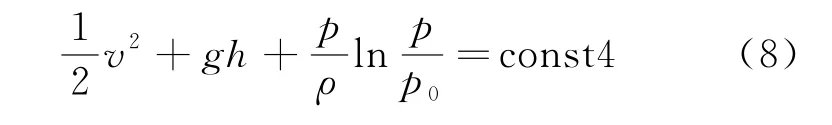
式(8)即等溫條件下理想氣體的伯努利方程。
利用伯努利方程的普遍性形式和等溫過程的物態方程也可以導出相同的結果,簡述如下。普遍形式的伯努利方程(又稱伯努利積分)為[1]
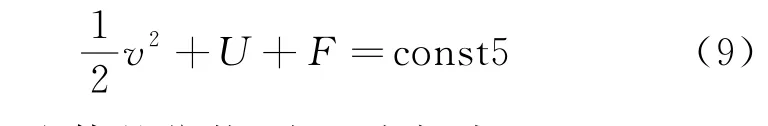
其中U為流體的位勢,在重力場中U=gh;F=為壓強的函數,具體形式由物態方程決定。對于等溫過程,將波義耳定律表示為p/ρ=const6,則
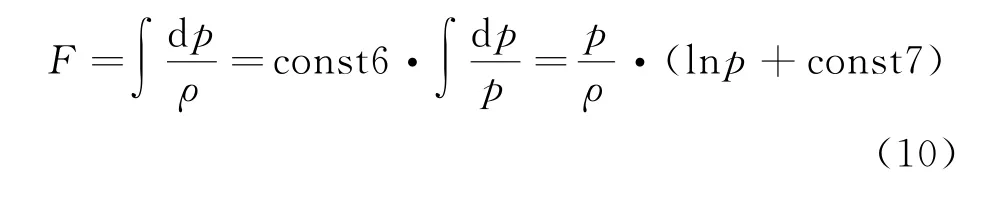
令const7=-lnp0可得
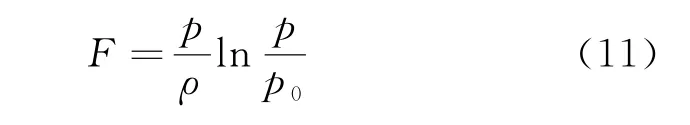
將U和F的表達式代入式(9)即得到式(8)。
利用理想氣體狀態方程
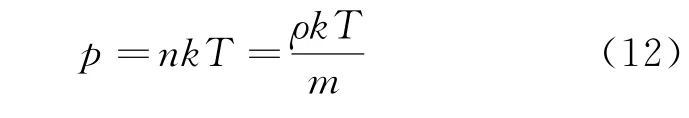
也可將式(8)等價地表示為
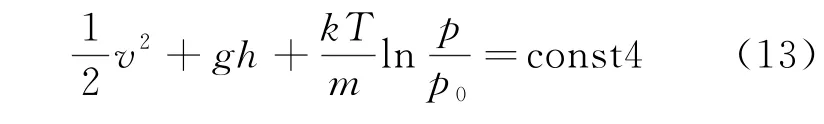
其中m為氣體分子質量,k為玻耳茲曼常量。在等溫過程中T為常量,利用式(12)可以更方便地說明流速與壓強的關系。顯然,即使在水平管道中,氣體的流速也并不恒定,而是和壓強有關,“流速大的地方壓強小”這一規律仍然成立。還應指出的是,式(8)的成立的必要條件是氣體的過程進行足夠緩慢從而和外界有充分的熱交換,這里的緩慢是就氣體的膨脹和壓縮過程而言,與流速v沒有必然關系。如果流管的截面積是緩變的,即使流速較大仍然可以按等溫過程處理。
4 結語
本文指出了《等》文在推導過程中存在的問題,并用兩種方法導出了在等溫條件下理想氣體滿足的伯努利方程,結果在形式上與理想流體的伯努利方程相近,為流線上三項之和守恒。結果還表明在高度差可忽略時流速大處壓強小這一性質對恒溫的理想氣體仍然成立。

