一種新的Glauber公式的證明方法

陶俊琦 王 蒙 程劍劍 鄭 華

(陜西師范大學物理學與信息技術(shù)學院,陜西 西安 710119)

Glauber公式在量子力學中有著十分重要的應用,特別是量子力學中的問題被轉(zhuǎn)化成算符操作后,比如利用平移算符作用在真空態(tài)上產(chǎn)生諧振子的相干態(tài)。Glauber公式給出了兩個算符之和的指數(shù)與算符指數(shù)之積的關(guān)系,它的具體表達式為

應用Glauber公式的條件是算符與算符分別與它們的對易子[]對易。由于量子力學中常見的坐標與動量算符、產(chǎn)生與湮滅算符之間都滿足Glauber公式的應用條件。因此Glauber公式是量子力學中十分重要的公式之一。對Glauber公式的證明也是非常重要的內(nèi)容。筆者通過對量子力學的學習與對大量量子力學教材和習題集的調(diào)研發(fā)現(xiàn)[1-22],對Glauber公式的證明方法主要有兩種。筆者認為這兩種方法都有其優(yōu)缺點,我們在正文中會做詳細討論。筆者在本文中通過構(gòu)造的方法,利用Baker-Hausdorff公式和算符的指數(shù)展開公式,給出了一種新的Glauber公式的證明方法。此方法不僅簡潔、簡單,同時具有思辨性,可以作為Glauber公式證明的另一種教學選擇。

1 Glauber公式常用的證明方法

量子力學教材中,第一種常用證明方法如下[2](注:不同教材和習題集的證明方法可能與下述證明方法略有不同,但本質(zhì)上屬于同一種方法)。先構(gòu)造一個含有參變量的算符指數(shù)的函數(shù)

其中λ為參變量。然后對參變量求導

利用Baker-Hausdorff公式

和算符與算符分別與它們的對易子]對易,可得

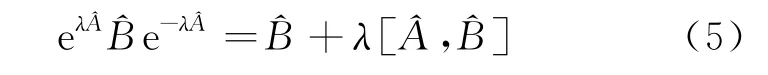
將式(5)代入式(3),可得

然后將(λ)除到式(6)左側(cè)的分母

對上式積分后得到滿足條件(0)=1的解為

在式(8)中令λ=1,即證明了Glauber公式

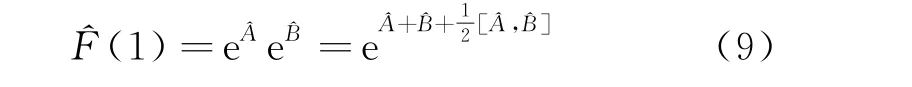
容易看出式(9)即式(1)的變體。

上述證明過程中,我們需要注意式(7)。在式(7)左側(cè)(λ)被除到了分母。(λ)是構(gòu)造的含有參變量的算符指數(shù)的函數(shù),然而與算符對應的矩陣是沒有除法的。這是筆者認為的此證明方法存在的一點瑕疵。但如果忽略式(8)的求解過程式(7),直接將式(8)代入式(6)進行驗證,此證明方法的瑕疵就消失了。

第二種常用的證明方法如下[14]。首先我們需要證明以下公式(詳細證明見參考文獻[14],在此我們就不贅述了)

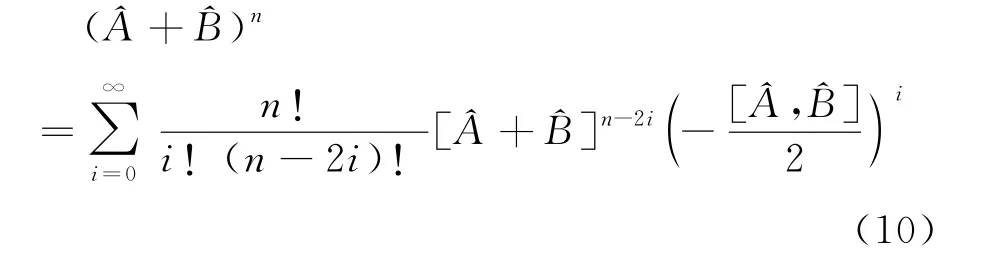
其中符號()n表示不能使用普通代數(shù)中的二項式定理進行展開,必須考慮算符的對易性質(zhì)。而符號[]n-2i表示不考慮算符與算符對易性質(zhì),可以用代數(shù)中的二項式定理展開,但算符一律寫在算符的前面。上述兩種符號相應的二次冪展開式如下

利用算符的指數(shù)函數(shù)展開,我們可以得到如下關(guān)系

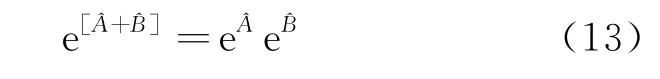
然后利用式(10)和式(13),即可直接證明Glauber公式

此證明方法非常嚴格,但需要提前證明式(10)和式(13)。如果考慮所有必須的證明過程,整個證明過程略顯復雜。

從上述兩種常用證明方法的討論中可以看出,兩種證明方法各有其優(yōu)缺點。第一種方法雖然簡潔明了,但存在一點瑕疵;第二種證明方法雖然嚴謹,但卻略顯復雜。筆者將在下文中給出了一種新的比較簡潔的Glauber公式的證明方法。

2 新的Glauber公式證明方法

利用Baker-Hausdorff公式(式(4)中令λ=1)可得

因此,可以構(gòu)造如下恒等式

將所有構(gòu)造的恒等式兩邊都乘以與其冪指數(shù)n相應的常數(shù)因子后相加并利用算符指數(shù)函數(shù)的展開式,可以得到

利用算符與算符分別與它們的對易子[]對易和式(16),可得

當算符與算符對易時,即[]=0,我們有。因此我們可以猜測,當算符與算符不對易時有

我們要求當[]=0 時,f([])=1。但f([])的具體形式是不知道的。由于我們所討論的是算符指數(shù)的運算,根據(jù)“物以類聚”的邏輯,自然的一種猜想為f([])=ex[],其中x為待定系數(shù)。式(23)可以寫為

將式(24)代入式(22)的右邊

對比最后兩行,只有當x=-時才成立。因此Glauber公式得證

3 結(jié)語

筆者對Glauber公式在量子力學教材中的兩種常用證明方法的優(yōu)缺點進行了相應的討論,并給出了一種新的證明Glauber公式的方法。該證明方法十分簡潔和簡單,只利用了Baker-Hausdorff公式和算符的指數(shù)展開公式,但需要加入一點思辨進行合理的猜想。這為學生學習證明Glauber公式提供了一種新的思路,同時對提高學生的創(chuàng)新能力也具有一定的啟發(fā)意義。