移動機器人平滑JPS路徑規劃與軌跡優化方法

黃健萌 吳宇雄 林謝昭

(福州大學機械工程及自動化學院， 福州 350116)

0 引言

隨著移動機器人被廣泛應用于農業等諸多領域，移動機器人導航技術逐漸成為研究熱點。路徑規劃是移動機器人完成導航任務的核心技術之一，其目的是讓機器人在充滿障礙物的復雜環境中找到從起點到終點的最佳無碰撞路徑[1]，通常是以規劃出的路徑最短作為優化目標。目前常用的路徑規劃方法有柵格法、人工勢場法、可視圖法等[2]，以及蟻群算法、粒子群算法等智能算法[3-4]。柵格法簡單有效，是目前使用最廣泛的一種方法。

柵格法中，Dijkstra算法[5]搜索時只考慮已花費成本，雖然能保證找到最短路徑，但會擴展大量無用節點。BFS算法采用啟發函數快速接近目標點，不考慮已花費成本，其效率高于Dijkstra，但不能保證找到最短路徑。A*算法[6]兼顧了兩者的優點，在考慮已花費成本的同時采用啟發式搜索，并能保證找到最短路徑。但A*算法規劃的路徑通常是一組曲折路徑，僅是離散空間上的最優解，與連續空間上實際最優解有較大差距。“視野線”法[7-9]常被用來對A*算法規劃的路徑進行平滑后處理，但只在后處理時使用平滑方法往往無法使路徑跨過障礙物，優化效果有限，平滑后的路徑有時仍與最優解存在較大差距。為此，Theta*算法[10]提出了任意角度規劃路徑的新思路，該方法在A*算法的基礎上，采取實時收縮父節點，即邊搜索邊平滑的策略，與采用后處理平滑的路徑規劃方法相比，能更好地接近最優解。在此基礎上許多學者進一步提出了Lazy-Theta*、Strict-Theta*、Batch-Theta*等Theta*類算法[11-13]，在效率和平滑處理等方面進行改進。由于Theta*類算法是在A*算法基礎上的改進，因此隨著柵格環境的增大，存在擴展節點急劇增加、搜索時間大幅延長的情況。文獻[14-16]提出的跳點搜索(Jump point search,JPS)算法采用了完全不同的節點擴展方式，與A*算法相比，JPS算法有效減少了需要維護的節點數量，尤其是在大柵格環境中，有效提高了尋路效率，但JPS所規劃路徑仍然只是離散空間的最優路徑。

采用柵格法規劃的路徑通常無法直接用于機器人運動，需進行軌跡優化處理。圓切線[8,17]方法雖然能生成可行軌跡，但并未考慮機器人運動的速度、慣性等物理參數。通過微分平坦[18]，多項式對各類機器人[19-20]在軌跡優化方面有著廣泛應用，相比單段多項式，多段多項式可以更好地適應復雜環境。文獻[21]利用多段高階多項式的特性將加速度相關導數作為優化目標。文獻[22-23]將多段多項式約束在安全范圍內，以避免軌跡發生碰撞。目前，主要依靠迭代獲取多段多項式軌跡優化的最優解。

本文在JPS算法的基礎上，提出一種平滑JPS(SJPS)算法。首先針對現有平滑方法的缺點提出一種路徑平滑方法，對JPS搜索規則進行修改，遍歷對稱路徑，并利用本文平滑方法對每條所得路徑進行平滑處理，再權衡長度與角度兩指標，最后對所得初始路徑用多段多項式進行軌跡優化，改進時間分配問題，加快迭代效率，并結合SJPS的特點對端點進行合理約束。

1 路徑平滑

“視野線”方法在部分情況下存在去除必要節點，留下冗余節點的問題。如圖1所示，路徑上每個柵格中心點均為路徑點，若按“視野線”方法平滑，則路徑將無改變，因為起點與轉折點連線檢查會將原本必要的節點去除。為得到穩定且良好的平滑效果，本文提出以2個目標對路徑點序列進行優化，即路徑每個折角處均在障礙物柵格的頂點上，且與路徑轉角進行接觸的障礙物位于轉角小于180°一側。

1.1 路徑單側有障礙物的情形

本文路徑平滑遵循以下步驟：

(1)將起點作為平滑路徑點的第1個點，記為qc(xc,yc)。

(2)將qc依次與后續JPS路徑點連接，直到找到連線Lm經過障礙物，對應連接路徑點qm(xm,ym)，并記錄前一條沒經過障礙物的連線Lm-1，對應路徑點qm-1(xm-1,ym-1)，并將點qm-1和qm之間的路徑離散成單個柵格移動的路徑點。若連接到了終點也未經過障礙物，則終點為最后一個平滑路徑點，結束搜索。

(3)再將點qc依次與步驟(2)中離散的路徑點(包括qm)連接，直到找到一條經過障礙物的連線作為新的Lm，對應連接點作為新的qm，前一條連線記為新的Lm-1，對應路徑點為新的qm-1。

(4)從Lm經過的障礙物柵格中，從可能頂點中找到一柵格頂點qj(xj,yj)，使點qc和qj的連線與Lm的夾角達到最大，則qj為新的平滑路徑點。將qj作為新的起始點qc從步驟(2)開始新一輪搜索。

以圖2的情況為例，首先將起點作為第1個平滑路徑點，并作為搜索起點qc，從第2個點(4,5)開始，將后續路徑點依次與qc連接，每次與qc連接的點記為qm。直到連接qc(2,3)和點(8,11)時，其連線經過障礙物，則將兩點間的路徑離散成單個柵格移動的路徑點，再將點qc依次與離散的路徑點連接。連接到點(5,8)時，兩點連線經過障礙物柵格(5，7)，記為Lm。然后選取障礙物柵格左上角頂點(4.5,7.5)作為下一個平滑路徑點，并以其為新的起始點繼續搜索。點(4.5,7.5)作為起始點搜索時，連接到終點也未經過障礙物，因此將終點作為最后一個平滑路徑點。最終產生的平滑路徑即圖2中的虛線路徑。

1.2 平滑路徑點選取

對于步驟(4)中障礙物柵格頂點的選取，使用一定的規則。如圖3所示，當經過障礙物的連線Lm非水平或垂直時，挑選連線上經過的障礙物，連線水平或垂直時，則只挑選第1個遇到的障礙物柵格。對于挑選的柵格(xobs,yobs)，每個柵格有4個頂點，但對于每次平滑路徑點搜索只有一個方向的頂點有可能被選取，延用步驟(2)中的qm-1、qc和步驟(3)中的qm標記，可能被選取的頂點應落在由qm、qc和qm-13點形成的三角形區域內。若步驟(2)中沒有按要求離散，則三角形區域將存在被遺漏的障礙物柵格。如圖4所示，頂點的選取有16種可能情況。先將點qm到點qc和qm-1方向的兩向量Vm,c和Vm,m-1叉乘判斷兩向量的順逆時針關系，再根據qm和qc連線斜率和Vm,c的朝向選擇頂點(xj,yj)

(1)

(2)

(3)

(4)

(5)

式(1)分別對應圖4中的16種情況，對應情形的向量位于哪一側則選取該側頂點。

選出各障礙物柵格頂點(xj,yj)后，將其與qc連線，并求其連線與Lm的夾角θ為

(6)

其中

V1=[xm-xc,ym-yc]

(7)

V2=[xj-xc,yj-yc]

(8)

從所有夾角中選出最大夾角所對應頂點qj作為下一個平滑路徑點和新的搜索起點qc。

1.3 路徑雙側均有障礙物的情形

當路徑雙側均有障礙物時，可能出現如圖5a所示情況。圖5a中虛線路徑為按上述規則優化后的平滑路徑，圖5b中虛線為理想平滑路徑。可知最后一個轉折處，轉折角小于180°處所在區域并無障礙物，不滿足第2個目標。這是因為尋找第3個新路徑點時，在從終點開始逐個連線進行搜索的過程中，受到了右側障礙物的干擾。

為此，在上述平滑路徑搜索步驟中增加1個局部平滑步驟。每3個連續路徑點產生一折角，從第3個新路徑點開始，每產生一個路徑點O3(x3,y3)，則設其前2個點依次為O2(x2,y2)、O1(x1,y1)，W1(W2)為O2指向O1(O3)的單位向量。如圖6所示，3點連線在障礙物一側的夾角為

θ′=α+β+γ=90°+β+γ

(9)

若該轉角θ′<180°，則有

β+γ<90°?β<90°且γ<90°

(10)

因此在圖6所示的局部坐標系下，W1(W2)總指向第三(一)象限，則2個單位向量的和向量W12(x′12,y′12)滿足

(11)

由式(11)可知，W12總指向局部坐標系第四象限，即障礙物應在象限，于是可得符合要求的轉角所對應的障礙物坐標(xp,yp)為

(xp,yp)=round((x2,y2)+W′12)

(12)

式中W′12——W12的單位向量

round()——四舍五入函數

通過上述方式可判斷O2處所在轉角小于180°一側對應柵格是否為障礙物，其他方向判斷與此同理。

(13)

式中 ceil()——往正無窮大方向取整的函數

步長s過長將導致選取平滑路徑點時遺漏障礙物。

2 平滑JPS算法

2.1 搜索規則

平滑JPS(SJPS)算法與原JPS算法相比有以下區別：

(1)終止條件。在開放列表第1次彈出終點時，SJPS不停止搜索，將第1次得到的路徑(未平滑)的長度作為約束值fz=l1，繼續擴展所有使啟發函數滿足f(n)≤fz的跳點，以遍歷已搜索路徑，直到不再有滿足要求的跳點。圖8是一個簡單的例子，圖8a為JPS路徑。在SJPS中，終點被彈出前，只有跳點1、2、3、4和起點被彈出，終點首次被彈出后將計算當前所得路徑，即圖8a路徑的長度，作為約束值fz，繼續擴展開放列表中滿足f(n)≤fz的跳點，因此跳點5將繼續被擴展。

(2)更新與記錄父節點方式。1個跳點可能被2個以上跳點所擴展，在JPS中，只記錄使啟發函數最小的跳點，舊父節點將被完全舍棄，而在SJPS中，被舍棄的父節點將被單獨保存，僅在回溯路徑時被使用，并且即使被擴展跳點已處于關閉列表仍然會進行更新。

(3)路徑回溯。在JPS中，終點被彈出后，從終點開始循環查找父節點，直到找到起點。在SJPS中，如區別(2)所述，回溯路徑時1個節點可能有多個父節點，此時將對每個父節點均進行路徑回溯。如圖8b，終點有2個父節點為跳點3和5，回溯路徑如圖8b所示兩條對稱路徑。每條回溯的路徑，均對其進行平滑處理，如圖8c所示。最后從所獲平滑路徑中，選取最理想的路徑為最終路徑，如圖8d所示。

2.2 路徑選擇

大多數路徑規劃方法都以長度作為指標進行尋找，但在一些情況下，更長一點的路徑可能會有更少的轉折和總轉角。因此，設立閾值Lz，對于每一條回溯的路徑，在平滑后記錄其長度和總轉折角。先將第1條平滑路徑作為當前路徑長度lnow和總轉折角φnow，然后遍歷其余平滑路徑長度lother和總轉折角φother進行對比，若滿足約束條件

(14)

式中w1——角度傾向權重

w2——長度傾向權重

其中之一，則將lother和φother作為新的lnow和φnow，對應路徑作為新的當前路徑，并繼續遍歷對比。最后所得當前路徑則為最終路徑。

3 軌跡優化

3.1 基于多段多項式的軌跡優化

直線路徑不利于機器人的運動，在SJPS規劃路徑基礎上利用多項式進行軌跡優化處理。將多項式各階導數作為軌跡的位置、速度(v)、加速度(a)和加加速度(j)等參數，單段多項式難以適應較為復雜的環境，因此使用多段高階多項式可以更好地在各種場景進行軌跡優化。為了能限制加速度導數，使用五次多項式。使用多段多項式平滑路徑，首先將軌跡按路徑點分段，設共分成m段。每小段路徑擬合為一多項式曲線，則對第n段路徑有

(15)

對于整條路徑，則有

(16)

式中T0、T1、…、Tm——路徑端點代表的時刻

由式(16)可知，通過求導可得任意時刻t的位置(P=f(t))、速度(v=f′(t))等參數并施加約束。結合本文平滑路徑點的特點，先約束多項式曲線經過起、止點，再限制其他路徑點只朝向與其接觸的障礙物相反的方向(如1.3節所述與W12相反的方向)

(17)

式中Pi——第i個路徑點

S——約束放寬的長度

m段多項式對應m+1個路徑點，約束的放寬對解的質量有重要影響。每個路徑點只限制了一段多項式曲線，因此需施加連續性約束，使不同段的多項式曲線在路徑點處位移、速度和加速度連續

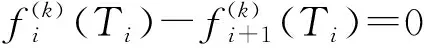
(18)

可根據需要選取最小化目標函數的導數階數，此處以最小化j為目標以增加運動平穩性，因此軌跡優化問題將轉換為如下最優化問題

(19)

該優化問題屬于QP問題。優化后的一些物理量可能超過預設值，可對優化后的時間比例乘一系數

(20)

式中M——速度等物理量預期值

2月7日，水利部與中國氣象局在京簽訂《關于加快水利和氣象發展的合作備忘錄》。雙方將加強合作與信息共享，推進水利跨越式發展，加快氣象現代化建設，促進水利、氣象事業全面協調可持續發展，共同提高國家綜合防災減災能力和水平。水利部部長、黨組書記陳雷，中國氣象局局長、黨組書記鄭國光出席簽字儀式并代表雙方簽訂備忘錄。

以此控制相關物理量的最高值，這不會影響優化的效果[24]。

優化時的軌跡存在重新碰撞障礙物的可能，可通過約束多項式端點的方式避開障礙物。如圖9所示，當某段軌跡被檢測到碰撞后，進行連線檢查，當有連線未經障礙物時，將該連線端點，及上一經過障礙物的連線的其中一個端點，3個點作為路徑點按前述方法做平滑，得到新的平滑路徑點作為軌跡的約束，使軌跡經過該點。

3.2 時間分配

上述QP問題，實際上可以看作是尋找最優時間分配問題。通常先給定一個時間分配初值，再用迭代的方法尋找最優解。對于時間初值的給定，目前有采用均速運動推算時間，即按路徑長度比例分配時間的方法[21]，雖然能收斂到最優解，但缺乏合理性，初值與最優解偏差較大，將增大迭代難度，增加運算時間。合理的時間初值可以大大減少迭代次數。

針對起止為靜止狀態的時間分配，設移動機器人從起點開始，平穩加速到最大允許速度時均速運動，接近終點時再平穩減速。若以最小化j為目標，則加速期間加速度應有一個平緩的變化率，因此借助余弦函數設加速度函數為

(21)

(22)

式中wj——期望的最大j值

vmax——最大允許速度

且從靜止加速到最大允許速度的時間為2π/wv。為使加速度不大于給定值amax，令

(23)

到達最大允許速度前的位移函數為

(24)

優化后的軌跡往往長于初始軌跡，因此將初始路徑乘一常系數ws，即s′i=wssi，并令sinit=spro1(2π/wv)，對于首段位移的時間分配，有

(25)

末段位移時間的計算與首段位移同理。對于首、末段之間位移s′i的時間分配則有

(26)

式中SFsum、SBsum——s′i之前、之后的位移

TFsum、TBsum——s′i之前、之后的累計時間

4 仿真與實驗分析

Matlab R2019b提供了ROS與導航相關工具箱，為驗證本文方法，在 I5-6300HQ型便攜式計算機上使用Matlab R2019b軟件與ROS平臺對本文算法進行仿真與實驗。

4.1 與Lazy-Theta*對比

Theta*類算法為得到更短的路徑，通常將路徑點設置于柵格頂點而非中心點。為方便對比，將SJPS的起始點在平滑前設置為當前柵格的柵格頂點，使其與Lazy-Theta*的起始點一致。此處SJPS在路徑選擇中，將Lz設為1倍柵格長度，w1、w2均設為30，啟發函數采用歐幾里得距離。Lazy-Theta*為八鄰域搜索，啟發函數同樣采用歐幾里得距離。在長寬為40×40場景隨機分布40個邊長為1.5倍柵格長度的方形障礙物，以不同精度劃分為柵格環境分別進行20次實驗并取平均值，結果如圖10所示，圖10橫坐標為橫/縱柵格數。

由圖10a可知，與Lazy-Theta*相比，SJPS的路徑長度稍短，總體較為接近。SJPS平滑性[25](總轉折角)明顯低于Lazy-Theta*。由圖10b可知，Lazy-Theta*和SJPS在低柵格精度時，搜索效率接近，隨著柵格精度提高，Lazy-Theta*的運行時間因為搜索節點大幅增加而急劇增長，而SJPS得益于跳點搜索，運行時間隨精度的提高上升較為平緩。其中柵格數為400×400時，Lazy-Theta*的平均運行時間為21.897 s，SJPS的平均運行時間為0.247 s。

4.2 與JPS對比

在長寬為40×40場景隨機分布160個邊長為1的方形障礙物并劃分為100×100柵格環境，在該環境進行的SJPS與JPS對比示例如圖11所示。

圖11b SJPS在路徑選擇中，將Lz設為1倍柵格長度，w1、w2均設為30，啟發函數兩者均為歐幾里得距離。如圖11a所示,僅在后處理對路徑進行平滑，無法使路徑跨越障礙物，除非將平滑處理變成另一意義上的路徑規劃，因而很難接近實際最優解。圖11b中，SJPS通過挑選有價值的路徑，以本文方法逐一進行平滑，再以一定方法進行路徑選取，以此可以得到更好的路徑。將障礙物數量設為160(10%障礙物)、320(20%障礙物)和480個(30%障礙物)分別進行20次實驗并取平均值，其數據如表1所示。由表1可知，與平滑后處理的JPS相比，SJPS對長度和總轉角有改善作用，運行時間增加7.06%～10.60%。對使用后處理的JPS，后處理的時間為0.8～1.2 ms。

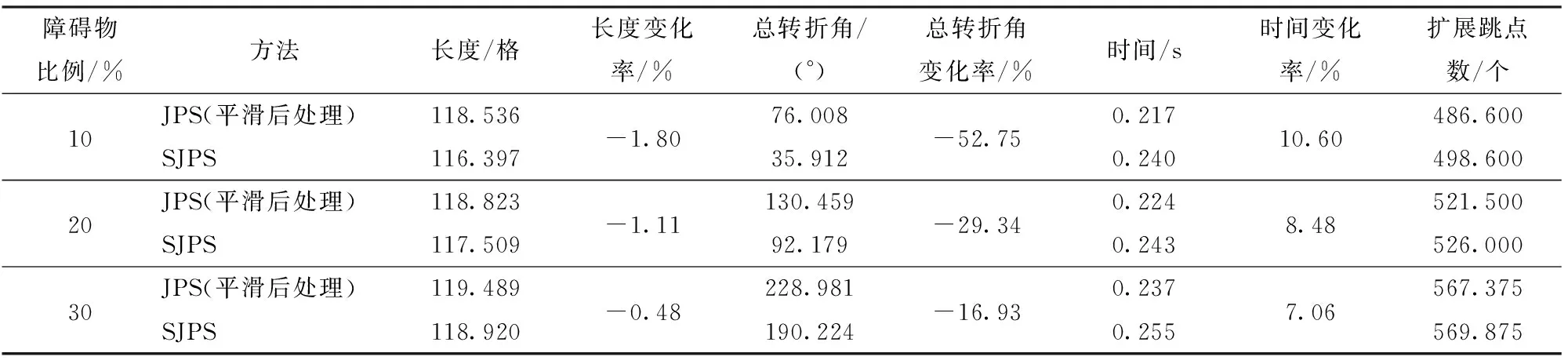
表1 100×100柵格環境下比較結果Tab.1 Results comparison in 100×100 grid environment

4.3 軌跡優化

對圖11b所得SJPS路徑進行軌跡優化，設起點和終點為靜止狀態，以柵格長度為單位，允許速度、加速度最大值分別為vmax=0.25 m/s、amax=0.25 m/s2，wj為1，ws為1.1，結果如圖11c所示。其中實線為最終優化結果，虛線為本文方法初始解(未考慮碰撞)，與最終解貼合程度較高，星號線為相同總時間下按路徑比分配時間的初始解(未考慮碰撞)，與最終解偏差較大。兩種初始解均能收斂于同一最優解。

圖11c的3種解對應規劃軌跡的速度、加速度、加加速度如圖12所示。本文方法初始解與最終解的各項參數吻合程度較好，采用路徑比分配時間初始解的方法，在首、末段軌跡帶來較大沖擊，從而影響了其他軌跡。但通過迭代，兩種初始解均獲得了同一最優時間分配，最終結果符合最小化加加速度的目標。本文所得初始解在第7次迭代接近最終解，耗時約1.2 s。按路徑比方法所得初始解，在第37次迭代收斂于同一最終解，耗時約6.5 s。

4.4 實驗驗證

使用兩輪差速移動機器人，利用Matlab與ROS對移動機器人進行聯合控制并將相關數據發送到Matlab，在如圖13a所示的環境進行實驗，基于Gmapping方法建立如圖13b所示柵格地圖，設膨化安全距離0.12 m，vmax=0.15 m/s、amax=0.15 m/s2，wj為0.5，ws為1.05，起點為(0,-0.98 m)，終點為(3.04 m,-1.54 m)。實際跟隨誤差約為0.015 m,規劃最高車速0.150 m/s,最大車速跟隨誤差約0.015 m/s。

5 結論

(1)提出一種平滑JPS路徑規劃方法，將改進后的JPS算法與本文的平滑方法相結合，對路徑增設了角度指標，以較小的長度犧牲,換取平滑性更為良好的路徑。結果表明，在不同障礙物密度環境下SJPS相對平滑后處理的JPS長度減少了0.48%～1.80%，總轉折角減少了16.93%～52.75%，搜索時間增加7.06%～10.60%。與Lazy-Theta*的對比結果表明，隨著柵格環境精度的提高，SJPS的搜索時間增加較為平緩，不會出現搜索時間急劇增加的情況，且SJPS路徑亦具有良好的平滑性。

(2)使用多段高階多項式對初始路徑進行優化，結合余弦函數提出了一種時間分配方法，可以更好地加快迭代速度，并結合SJPS的特點對多項式端點進行約束。通過仿真及實驗驗證了本文方法的可行性。