公路路基邊坡穩(wěn)定性分析及錨固優(yōu)化設(shè)計研究
高曉通
(新疆維吾爾自治區(qū)交通規(guī)劃勘察設(shè)計研究院,烏魯木齊 830006)
路基邊坡穩(wěn)定性是確保公路項目施工進度和安全運營的關(guān)鍵因素之一。 公路邊坡穩(wěn)定性易受到地形地貌、施工技術(shù)等因素影響,尤其是山區(qū)公路,往往會遇到較大規(guī)模的高填深挖,改變原有的地質(zhì)條件,可能導(dǎo)致滑坡、坍塌等地質(zhì)災(zāi)害,從而導(dǎo)致嚴(yán)重的經(jīng)濟損失及不良的社會影響。 選擇經(jīng)濟、合理、可行的邊坡防護措施,已經(jīng)成為工程技術(shù)人員需要解決的重要問題。 目前常用的路基邊坡加固方案主要有錨桿(索)框架梁、擋土墻、三維網(wǎng)植草、預(yù)應(yīng)力錨索(桿)、圬工防護等。
近年來,國內(nèi)外研究人員及工程師也通過理論公式計算、離心模型、原位監(jiān)測等措施來探討了巖土項目的錨固機理、加固效果及設(shè)計理念,并提出大量有價值的研究成果[1]。 但是,設(shè)計人員在開展公路設(shè)計任務(wù)時,仍以工程類比法為主,為了確保工程有較高的安全冗余度,設(shè)計方案一般較保守,從而導(dǎo)致工程費用過高, 故分析路基邊坡安全系數(shù)的變化機理及錨固方案優(yōu)化具有十分重要的工程意義。
1 邊坡穩(wěn)定性分析方法
1.1 極限平衡分析法
極限平衡法是公路項目中應(yīng)用最廣泛的一種路基邊坡計算方法,一般假設(shè)路基邊坡的潛在滑動面為直線或圓弧形,并根據(jù)邊坡邊界條件,對可能出現(xiàn)滑坡的若干個滑動面進行力學(xué)分析,建立土體強度和作用荷載之間的平衡條件,給出相應(yīng)的安全系數(shù)。 極限平衡法不能考慮巖土體的應(yīng)力歷史、加載-卸載過程等, 但其計算方法簡便、 計算結(jié)果可靠。 目前常見的極限平衡法一般包括瑞典條分法、畢普肖法、薩爾瑪法(SARMA)法[2]。
(1)瑞典圓弧法
瑞典條分法是假定土質(zhì)路基邊坡潛在滑動面為圓弧形,而分析巖體邊坡穩(wěn)定性時,必須是破碎或松散巖體才具備可行性,主要原因在于完整巖體邊坡的滑動面往往是折線形,與瑞典圓弧法的理論矛盾。
(2)畢普肖法
畢普肖法是對瑞典圓弧法的一種改進,同樣適用于滑動面為圓弧的土質(zhì)邊坡。 該方法是將滑坡體劃分成多個寬度相同的垂直條塊(如圖1 所示),并以滑動圓弧的圓心為力矩中心點,計算得到抗滑力矩與下滑力矩的比值即為邊坡安全系數(shù)[3]。

圖1 畢普肖法的力學(xué)分析
(3)SARMA 法
SARMA 法應(yīng)用較廣泛, 不僅能計算潛在滑動面為直線、折線、圓弧形的路基邊坡安全系數(shù),還能考慮以巖體的斷層、 節(jié)理等來劃分滑坡體的條塊,并能夠?qū)麻_展反分析,求出滑動面的粘聚力和內(nèi)摩擦角。
1.2 數(shù)值計算法
隨著計算機技術(shù)的飛速發(fā)展,數(shù)值計算法在巖土計算領(lǐng)域地應(yīng)用日益普遍, 一般包括有限元法、有限差分法、離散元法等,其中有限元法的應(yīng)用最廣泛[4]。 有限元法能用來計算巖土體的彈性、彈塑性、流變、大變形問題等,并能夠給出巖土體的應(yīng)力應(yīng)變大小和分布規(guī)律,以便于更好地分析路基邊坡的失穩(wěn)變形機制。
2 邊坡錨固機理及計算模型建立
2.1 錨固機理分析
研究成果表明,錨桿(索)加固技術(shù)可以充分發(fā)揮巖土體本身強度和潛力,控制工程變形,幾乎成為應(yīng)對公路邊坡失穩(wěn)破壞的最為經(jīng)濟、有效的措施之一。
天然狀態(tài)下的路基邊坡往往受到潛在滑動面以上巖土體切向力、滲透水及其他荷載,而其穩(wěn)定性主要是由邊坡可能滑動面巖土體的抗剪強度參數(shù)來維持[5-6]。 為了避免邊坡失穩(wěn)破壞,錨固力必須能使作用在滑動面上的所有力系保持平衡,即抗滑力矩大于下滑力矩,加固原理如圖2 所示:

圖2 邊坡錨桿加固機理

式中: f——土層的摩擦系數(shù),無量綱;
r——圓弧滑動面的半徑;
C——土層的粘結(jié)力。
由此可知,錨桿可以將滑坡推力傳遞到更深的穩(wěn)定地層中, 利用穩(wěn)定地層的錨固作用和被動抗力,使得邊坡保持穩(wěn)定狀態(tài)。 錨桿阻止滑坡體下滑主要源于潛在滑動面上錨桿與巖土體的相互作用,此時錨桿均可視作一個個約束點,每個約束點均可提供正壓力和上提力,前者可以阻止滑坡體與穩(wěn)定巖土體分離,后者可以阻止滑坡體的下滑。 當(dāng)這些約束點的數(shù)目、位置和強度布置合理時,才能夠充分發(fā)揮錨桿的錨固作用,使邊坡保持穩(wěn)定狀態(tài)。
2.2 邊坡計算模型建立
(1)邊坡地質(zhì)概況
依托項目為某山區(qū)公路,沿線地質(zhì)條件較為復(fù)雜,可能存在較多高陡路基邊坡。 路基邊坡的巖體基本都是強風(fēng)化泥質(zhì)粉砂巖, 完整性和穩(wěn)定性較差。 同時,根據(jù)區(qū)域地質(zhì)資料,場區(qū)處于相對較穩(wěn)定的地質(zhì)環(huán)境,場地土屬中硬土,無地震作用下的可液化地層,地震基本烈度為Ⅵ度,路基邊坡巖體的設(shè)計物理力學(xué)參數(shù)建議值見表1:
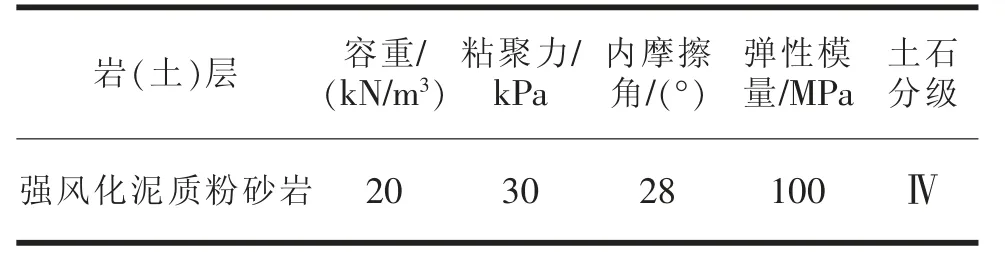
表1 強風(fēng)化泥質(zhì)粉砂巖計算參數(shù)
(2)計算模型
路基邊坡高度為20 m,分兩級(每級10 m)開挖,每級設(shè)2 m 平臺,坡腳為60°。 邊坡模型尺寸如圖3 所示:

圖3 邊坡計算模型
FLAC3D 軟件可以用cable 單元來模擬全長粘結(jié)錨桿結(jié)構(gòu)及其與巖體之間的接觸面,但應(yīng)當(dāng)將錨桿結(jié)構(gòu)進行簡化處理,即將錨桿視作理想的兩節(jié)點直線單元,且直線段的截面及材料參數(shù)完全相同。
3 支護參數(shù)對邊坡穩(wěn)定性影響分析
在確定設(shè)計參數(shù)、建模、劃分網(wǎng)格、設(shè)置邊界條件等工作完成之后,對邊坡穩(wěn)定性開展驗算,得到了天然狀態(tài)路基邊坡的安全系數(shù)為0.98,小于《公路路基設(shè)計規(guī)范》(JTG D30-2015)的規(guī)定值1.2,故需要進行加固處理。 路基邊坡加固應(yīng)按照“強腳固腰”原則[7],采用全長粘結(jié)錨桿對一級和二級邊坡進行防護,錨桿布置間距、長度對邊坡穩(wěn)定性的影響分析如下。
3.1 錨桿間距的影響
在錨桿長度(12 m)和錨桿傾角(15°)不變前提下,將錨桿布置在圖4 所示位置,各個位置相應(yīng)的高度分別為1 m、3 m、5 m、7 m、9 m、11 m、13 m、15 m、17 m、19 m。

圖4 錨桿布置位置示意圖
利用FLAC3D 得到了錨桿在邊坡不同位置處的軸力大小及相應(yīng)的安全系數(shù),見表2:

表2 錨桿軸力和安全系數(shù)計算結(jié)果
計算結(jié)果表明,隨著錨桿軸力的增加,錨桿的錨固效果變好,安全系數(shù)也不斷增大,且兩者之間基本呈線性正相關(guān)的關(guān)系。 這樣就可以利用錨桿軸力的差值來間接分析多根錨桿在不同布設(shè)間距下的錨固效果及其對邊坡安全系數(shù)的影響。
3.2 錨桿長度的影響
在錨桿長度縱向間距(2 m)和錨桿傾角(15°)不變的前提下,將錨桿按表3 來布置,分析長度分別為6 m、9 m、12 m、15 m、18 m、21 m 的錨桿加固下的邊坡安全系數(shù)變化規(guī)律。
計算結(jié)果表明, 當(dāng)邊坡錨桿加固長度小于15 m時,隨著錨桿長度的增加,邊坡安全系數(shù)也逐漸增大,但兩者之間為非線性正相關(guān);當(dāng)邊坡錨桿加固長度大于15 m 時, 邊坡穩(wěn)定性增長不明顯, 錨桿加固長度18 m 相對于15 m,邊坡的安全系數(shù)僅提高了1.21%,可以忽略不計;當(dāng)邊坡錨桿加固長度大于18 m 時,增加錨桿加固長度反而會導(dǎo)致邊坡的安全系數(shù)降低。

表3 錨桿軸力和安全系數(shù)計算結(jié)果
4 結(jié)語
(1)邊坡穩(wěn)定性分析方法主要有極限平衡法和數(shù)值計算法,前者包括瑞典圓弧法、畢普肖法、SARMA法等,后者包括有限元法、有限差分法、離散元法等;
(2)錨桿能傳遞滑坡推力傳遞到更深的穩(wěn)定地層中,使得邊坡保持穩(wěn)定狀態(tài),錨桿可視作一個個約束點,為滑坡體提供正壓力和上提力。 當(dāng)這些約束點的數(shù)目、位置和強度布置合理時,才能夠充分發(fā)揮錨桿的錨固作用;
(3)隨著錨桿軸力提高,錨桿地錨固效果變好,安全系數(shù)也持續(xù)增大,且兩者之間基本呈線性正相關(guān)關(guān)系;
(4)當(dāng)邊坡錨桿加固長度大于15 m 時,邊坡安全系數(shù)增加很小, 當(dāng)邊坡錨桿加固長度大于18 m時,邊坡穩(wěn)定性反而降低。 因此,從技術(shù)和經(jīng)濟兩方面來分析,該邊坡的錨桿加固長度可取15 m。

