匯流環底板動態特性分析*

文 廣，程 明,張學蓉，唐先春，蔣辛輝，李 航

(1.成都工業學院 智能制造學院，四川 成都 611730；2.成都無線電專用設備廠(國營633廠)，四川 成都 611730)

0 引 言

作為匯流環的重要零部件之一，底板主要承受來自于上方的壓力。除了底板外，匯流環內部還裝有環芯等轉動部件。由于零件的加工及裝配等工序中存在無法避免的誤差等原因，匯流環在工作時，包括底板在內的各零部件會承受一定的隨機振動載荷，因此，在進行匯流環結構設計時，有必要對包括底板在內的零部件進行動態特性分析。進行動態特性分析的方法有很多，常見的有試驗法和仿真分析法，其中，仿真分析法由于其低成本、操作方便等原因，在結構動態特性分析領域有著廣泛的應用。文獻[1]～[4]分別以某精密機床、某頂驅傳動系統的齒輪軸大齒輪、某小型電動汽車的輪轂和某叉車驅動橋橋體為研究對象，利用有限元軟件Ansys Workbench對其進行了模態分析，獲取了結構的模態振型和固有頻率等參數。文獻[5]為了研究某電動輪自卸車車架的靜動態特性，開展了多工況下的動強度、剛度和模態分析。文獻[6]則利用有限元軟件Ansys對某桁架式門機的靜動態特性進行了分析，獲取了結構的前六階固有頻率和振型。文獻[7]采用ADAMS軟件對某角接觸球軸承在不同徑向載荷、軸向載荷、角加速度條件下的加速過程進行了仿真。筆者使用有限元軟件Ansys對某匯流環底板結構的動態特性進行分析，獲取結構的模態固有頻率、振型及簡諧響應曲線，為該底板及匯流環整體的結構優化提供了數據參考。

1 匯流環底板結構示意及有限元模型

底板是匯流環的重要零部件之一，安裝在匯流環底部，其結構示意如圖1所示。該底板由鋁制成，其材料特性參數如表1所列。

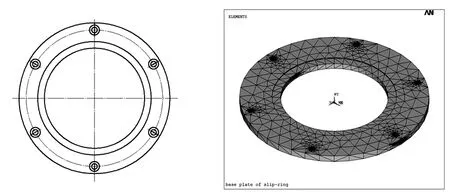
圖1 匯流環底板結構示意圖 圖2 匯流環底板有限元模型

表1 匯流環底板材料特性參數

基于匯流環底板的結構示意圖，在忽略底板上的倒角等較小結構后，按照有限元建模的思路，建立其有限元模型。整個底板結構采用Solid 187 實體單元模擬，實體模型建立后，選用自由網格劃分方式對其進行網格劃分，離散后的有限元模型如圖2所示，該模型共有49 075個單元，81 952個節點。

2 匯流環底板自振特性分析

文中主要利用Ansys軟件的模態分析模塊來開展匯流環底板的自振特性分析，根據有限元理論，模態分析主要用于獲取結構的固有頻率和振型等自振特性參數。該底板的動力學方程可以用下式來描述[8]：

(1)

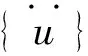
底板的模態分析采用蘭斯索斯法，分析結束后，提取底板結構的前六階模態固有頻率如表2所列及各階模態振型如圖3所示。

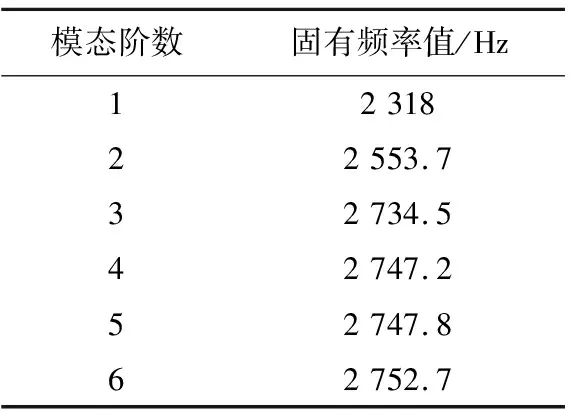
表2 底板模態固有頻率

圖3 底板模態振型圖

從圖3可以看出，該匯流環底板的前六階模態振型主要表現如下：第一階模態振型主要表現為底板中間部位的上下起伏振型，第二至第六階振型均表現為底板結構整體的扭曲振型。

3 匯流環底板諧響應分析

利用有限元軟件Ansys的諧響應分析模塊，對該匯流環底板結構進行簡諧振動分析。考慮到該底板前六階模態固有頻率最大值為2 752.7 Hz，因此，將外界激勵載荷頻率設置為0～2 760 Hz，間隔為10 Hz，激勵載荷的大小保持不變，即為階躍載荷，載荷施加位置如圖4所示。分析后，提取底板結構上部分關鍵節點的位移幅值響應曲線，如圖5所示。

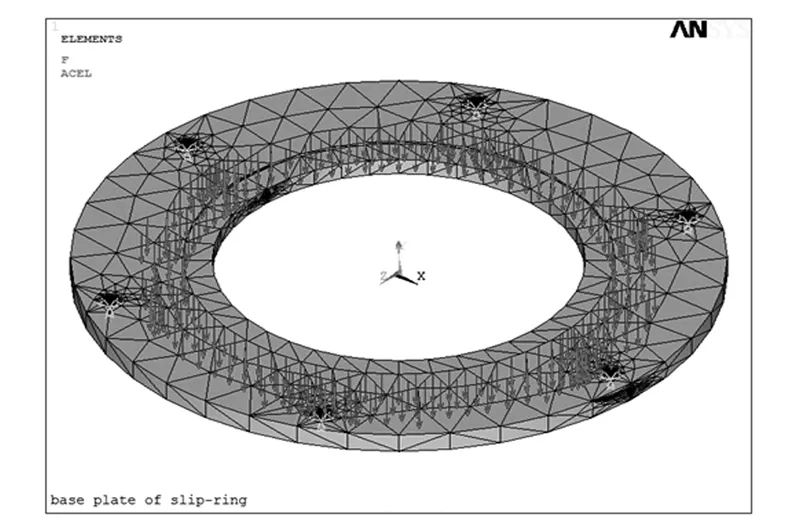
圖4 加載后的底板有限元模型

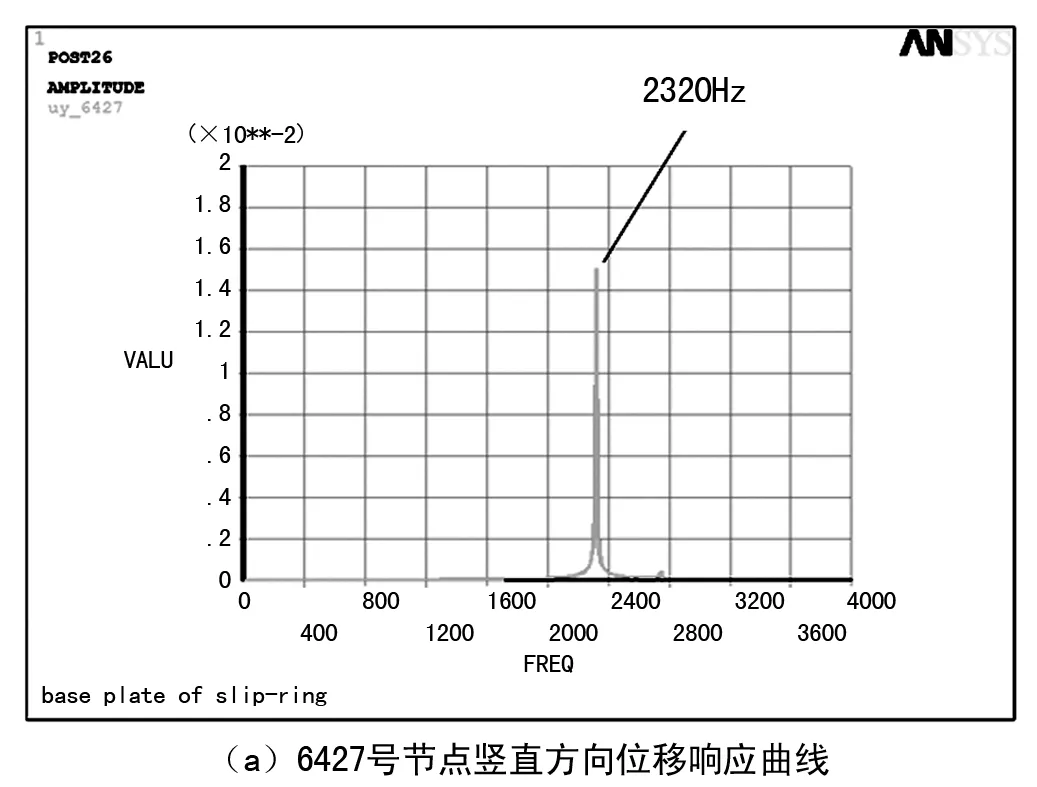
圖5 底板關鍵節點位移響應幅值曲線

從圖5可以看出，所有關鍵節點的位移響應幅值均在激勵載荷頻率約為2 320 Hz時，達到了最大，該激勵頻率和底板結構的第一階模態固有頻率值接近，因此，可以認為在該底板結構的前六階模態中，其第一階模態對其自身的動態特性影響最大。

4 結 論

利用有限元軟件對某匯流環底板結構進行動態特性分析，借助模態分析模塊和諧響應分析模塊分別獲取了底板結構的模態固有頻率、振型及位移響應曲線。通過計算分析取得如下主要結論。

(1)該匯流環底板結構的前六階模態固有頻率分別為：2 318、2 553.7、2 734.5、2 747.2、2 747.8、2 752.7 Hz。

(2)該底板結構的前六階模態振型主要表現如下：第一階模態為底板結構中間部位的上下起伏振型，其余各階振型均表現為底板整體的扭曲振型。

(3)該底板結構在激勵載荷頻率約為2 320 Hz時，其位移響應幅值達到最大，底板結構的第一階模態對其動態特性影響較大。