分數階不確定R?ssler 混沌系統的自適應滑模同步
毛北行,王東曉
(鄭州航空工業管理學院數學學院,河南鄭州450015)
混沌系統的同步控制廣受關注[1-4]。近年來,針對分數階混沌同步問題的研究不斷深入,并取得了一系列研究成果[5-9]。例如,文獻[10]研究了超混沌分數階Bao 系統的反饋同步;文獻[11]研究了一類分數階不確定Victor-Carmen 混沌系統的自適應滑模同步控制;文獻[12]基于比例積分滑模方法研究了分數階不確定超混沌Bao 系統的同步。在實際應用中,模型的不確定性、被控對象的結構變化、測量誤差以及外部擾動等均會影響系統的性能,因此,須考慮這些因素造成的影響。例如,文獻[13]研究了具有有界外擾和不確定項的分數階超混沌金融系統滑模同步的4種方法。R?ssler 混沌系統的同步亦廣受關注。例如,文獻[14]研究了基于back-stepping 方法對超混沌R?ssler 系統的控制與同步;文獻[15]研究了雙時滯R?ssler 系統的分支分析與混沌控制;文獻[16]研究了基于曲率指數的耦合混沌系統的完全同步分析。受上述結論啟發,筆者利用自適應滑模控制方法,研究了帶有模型不確定性和外擾的R?ssler混沌系統的同步問題,得到分數階不確定R?ssler 混沌系統取得適應滑模同步的充分條件,所得結論說明不確定R?ssler 混沌系統在一定條件下取得了自適應滑模同步。最后,用數值仿真實驗對結論進行了檢驗。
1 主要結果
定義1[17]Caputo 分數階導數定義為

以分數階R?ssle 混沌系統
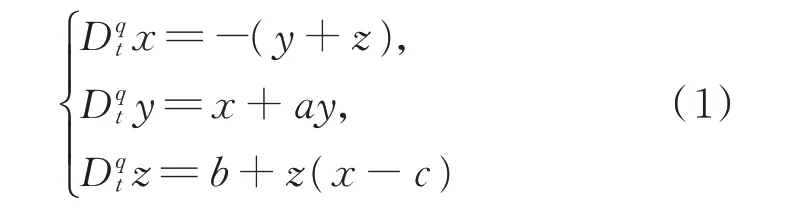
為主系統,當a=0.2,b=0.2,c=5.0,q=0.92 時,系統的時域波形圖和相平面圖分別如圖1 和圖2 所示。
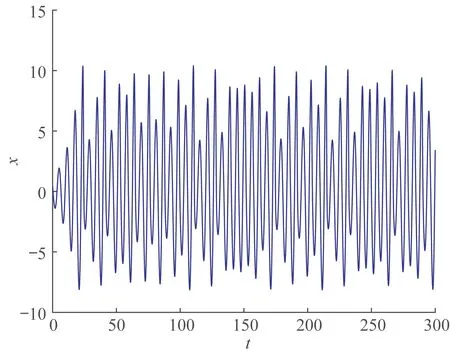
圖1 系統的時域波形圖Fig.1 Time domain of the system
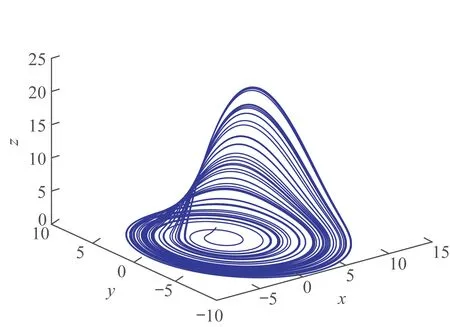
圖2 系統的相平面圖Fig.2 Phase plane of the system
從系統為
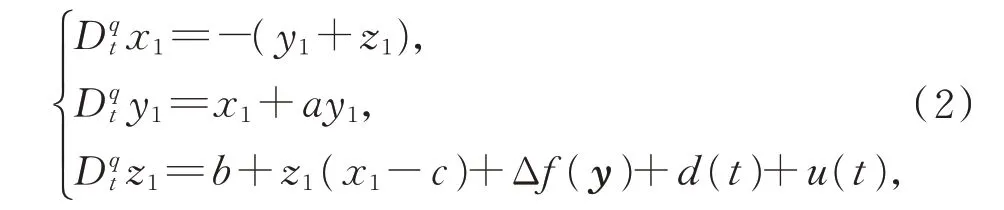
其中,不確定項Δf(y),y=[x1,y1,z1]T,d(t)為外擾,u(t)為控制器。定義
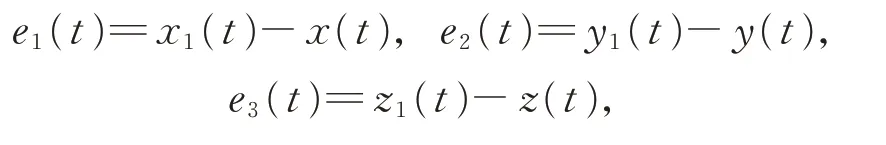
得到誤差方程:
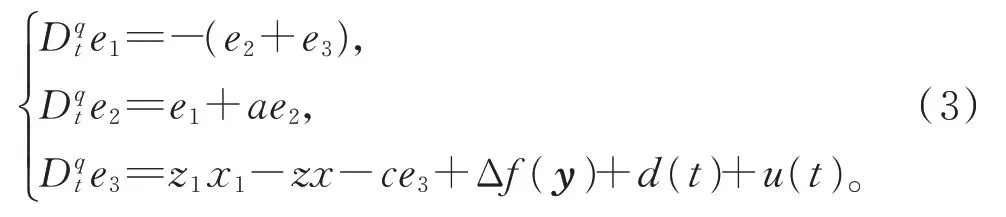
假設1假設不確定項Δf(y)和外部擾動d(t)有界,即存在未知參數m,n>0,使得
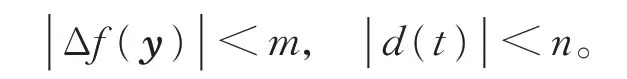
引理1[18]若x(t)為連續可微函數,則有
引理2[18]設其中,y1(t),y2(t)∈R 具有連續一階導數,若存在常數k>0,使 得有界,且其中,Eα,1(·)表 示 雙 參 數Mittag-Leffler 函 數,則y1(t)具Mittag-Leffler 穩定且
定理1在假設1 條件下,設計滑模面s=設計控制器
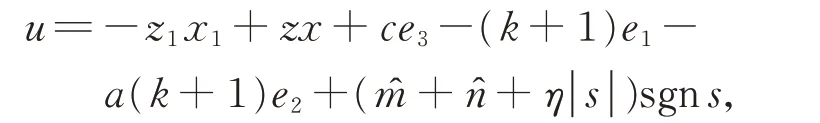
其中,?分別為m,n的估計值,η>0。則式(1)和式(2)適應滑模同步。
證明滑模面上由式(3)第1 個方程,得?(e2+e3)=ke2。
進一步得到e3=?(k+1)e2,對式(3)第2 個方程兩邊同求q階微分,得到因 為所 以利 用 Laplace 變 換 ,記E2(s)=L(e2(t)),則有
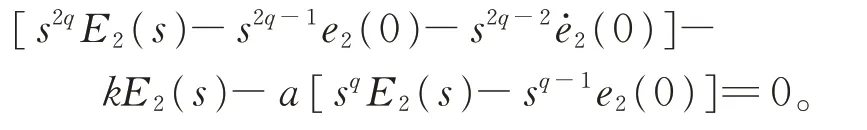
由Laplace 終值定理,有
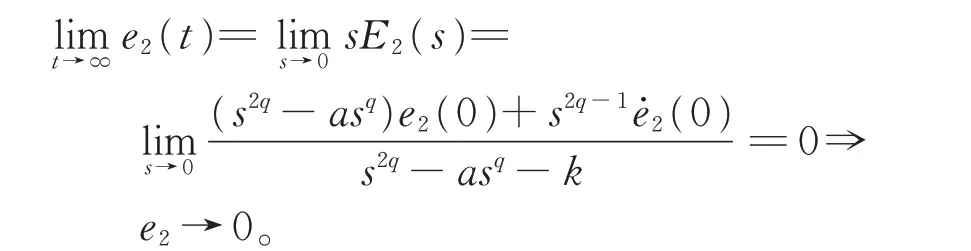
由 于e3=?(k+1)e2?e3→0,且e2→0 ?,將 其 代 入 式(3)第2 個 方 程,有=e1+ae2?e1→0。
所以,定義的滑模面具有穩定性。
下證滑模面的可達性。

由引理2,有s→0。
以整數階R?ssle 混沌系統
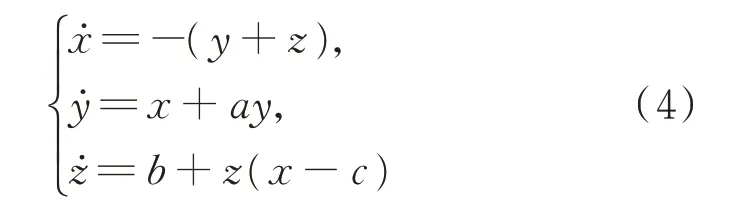
為主系統,從系統為

定義
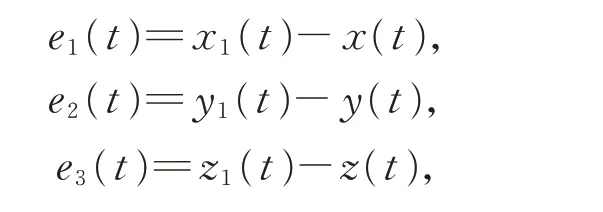
得誤差方程
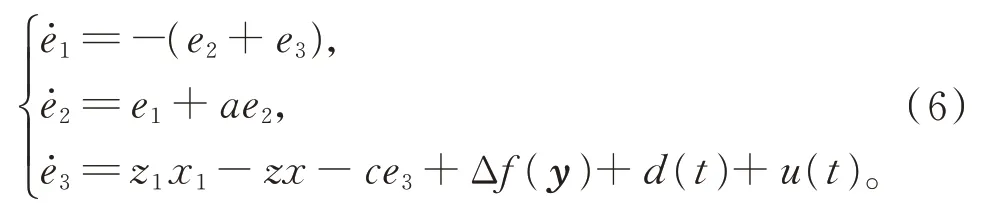
引 理3(Barbalat’s)[19]若 函 數f(t) 在[0,+∞)上一致連續,且廣義積分存在,則其中,f(t)為一致連續函數。
定理2在假設1 條件下,設計滑模面s=設計控制器
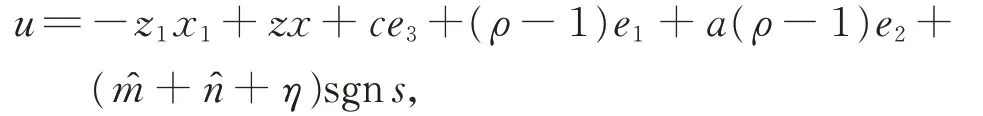
其中,?分別為m,n的估計值,η>0。則式(4)和式(5)適應滑模同步。
證 明滑 模 面 上即?(e2+e3)=?ρe2,進一步得到e3=(ρ?1)e2,對式(6)第2 個 方 程 求 一 階 微 分,得 到因為所 以以e2(t)為變量,則其特征值由于ρ<0,所以又由于混沌系統軌跡有界,所以|e2(t)|必有界,從而必 有C1=0。 否 則,若C1≠0 ?e2無 界,易 得由 于e3=(ρ?1)e2?e3→0, 將代入式(6)第2 個方程,得到e1→0。
所以,定義的滑模面具有穩定性。
下證滑模面的可達性。
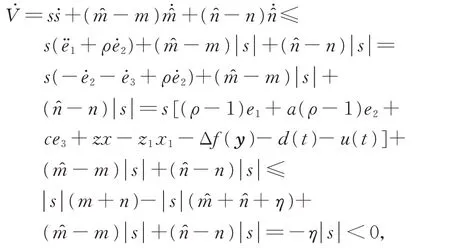
證畢!
2 數值仿真
以MATLAB 仿真程序對上述系統進行數值仿真,選取初始值及系統參數為
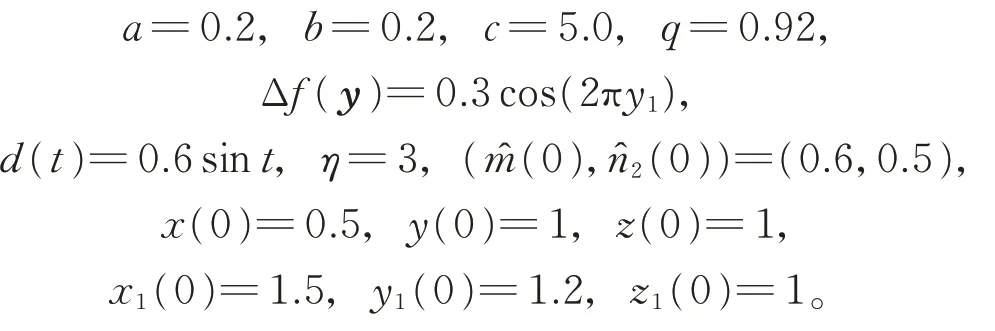
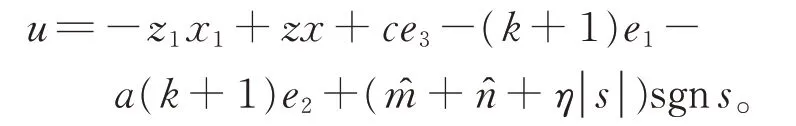
在定理2 中,設計滑模面
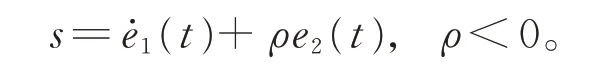
在定理1 中,設計適應律
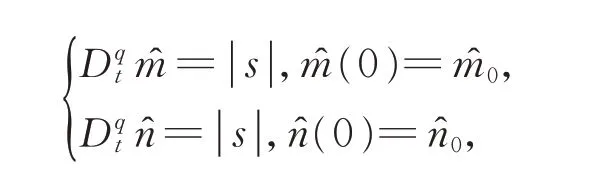
在定理2 中,設計控制器
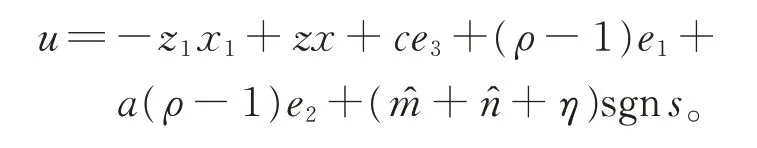
在定理2 中,設計適應律
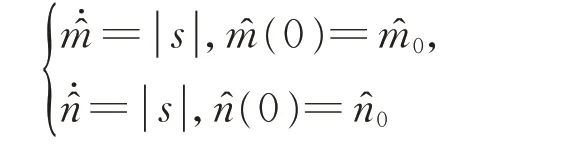
定理1 和定理2 的誤差分別如圖3 和圖4 所示,由圖3 和圖4 知,初始時刻誤差相差較大,距離原點較遠,隨著時間的推移,誤差逐漸趨于一致,趨向坐標原點,表明系統取得了滑模同步。
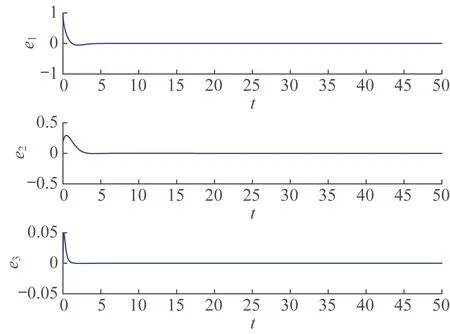
圖3 定理1 的誤差Fig.3 Errors in theorem 1
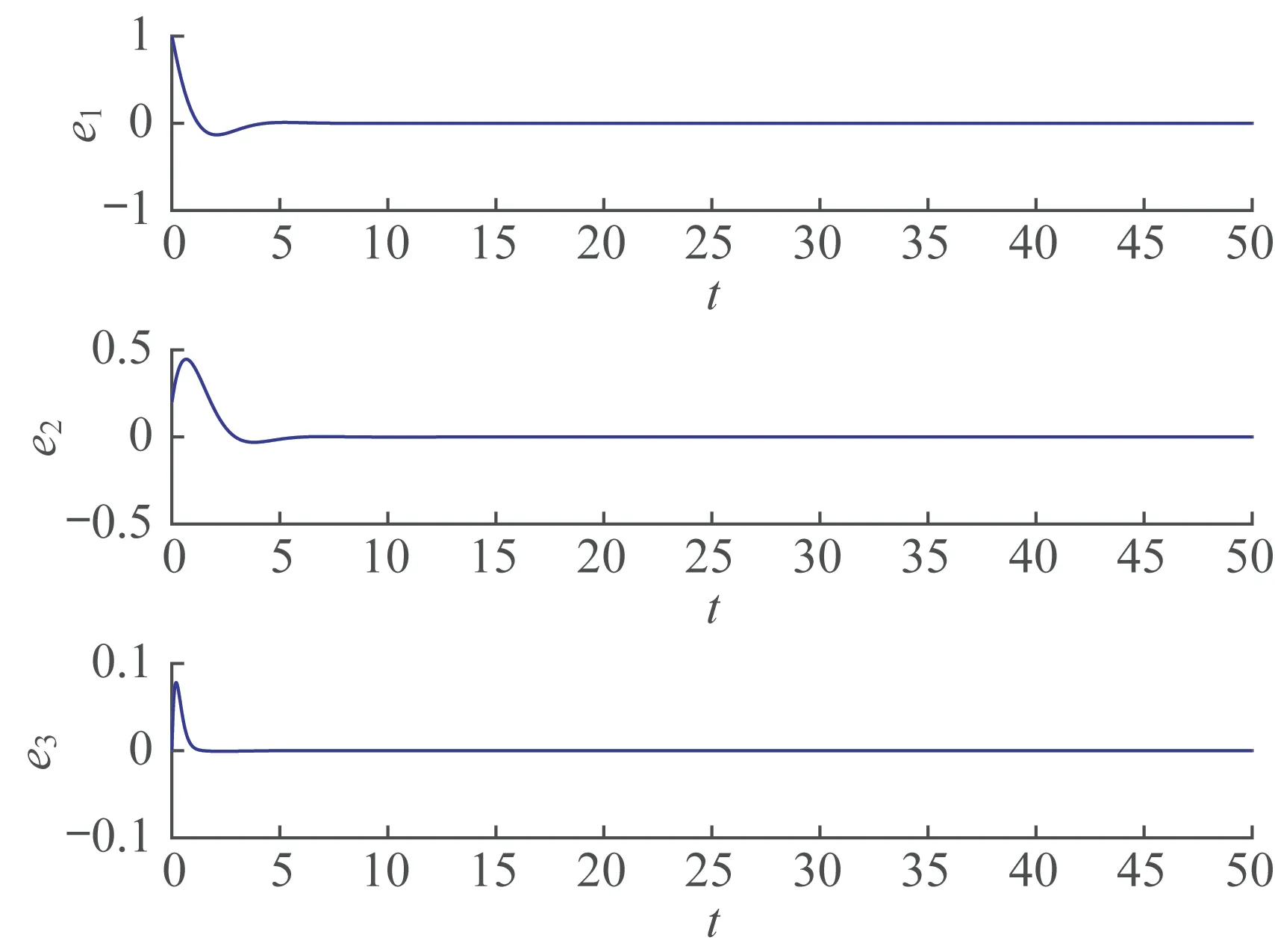
圖4 定理2 的誤差Fig4 Errors in theorem 2
3 結 論
研究了具有模型不確定性和有界外部擾動的分數階不確定R?ssler 混沌系統的自適應滑模同步問題。通過構造適當的滑模面、控制器和適應律,得到分數階不確定R?ssler 混沌系統的自適應滑模同步的充分條件。本文方法不僅適用于分數階混沌系統,而且可平推至整數階系統。

