一類不確定半無限多目標優化問題的魯棒逼近最優性

莫曉慶,孫祥凱

(重慶工商大學 經濟社會應用統計重慶市重點實驗室,數學與統計學院,重慶 400067)

設T為非空無限指標集,fi:n→(i=1,2,…,m)和gt:n→(t∈T)是局部Lipschitz函數,考慮下列半無限多目標優化問題：

半無限多目標優化問題(MP)在數學物理、工程設計、經濟管理、合作博弈等領域應用廣泛,目前已取得許多研究成果[1-5]. 但在處理實際問題時,由于測量等因素的影響,很難保證問題(MP)的目標函數或約束函數中所含數據的精確性. 因此,含有不確定性信息的多目標優化問題研究得到廣泛關注. Chuong[6]借助變分分析工具和廣義凸性假設,研究了非光滑魯棒多目標優化問題Pareto有效解的最優性條件和對偶性定理; Fakhar等[7-8]借助一類極限次微分和一些合適的廣義凸性假設條件,研究了一類約束函數帶有不確定信息的多目標優化問題的最優性條件、對偶性定理及鞍點定理; Lee等[9]借助共軛函數的上圖技巧通過引入一類新的閉性條件,刻畫了不確定半無限多目標優化問題的魯棒最優性條件和Wolfe型魯棒對偶性；Chen等[10]借助一類約束標量化方法,刻畫了不確定多目標優化問題的有效解及弱有效解的魯棒最優性條件；Sun等[11]借助一類標量化方法和廣義凸性假設,刻畫了一類非光滑非凸多目標優化問題的魯棒逼近Pareto有效解的充分最優性條件、Wolfe型魯棒對偶性及魯棒鞍點定理. 但上述研究主要針對不確定多目標優化問題的魯棒有效解展開,而針對含有不確定參數的半無限多目標優化問題的魯棒逼近擬Pareto弱有效解的研究尚未見文獻報道.

考慮問題(MP)的不確定參數模型:

其中:ui∈Ui(i=1,2,…,m)和vt∈Vt(t∈T)為不確定參數,Ui?m(i=1,2,…,m)和Vt?q(t∈T)為不確定集合;fi:n×m→(i=1,2,…,m)和gt:n×q→(t∈T)為局部Lipschitz函數. 本文若無特殊說明,記

本文借助魯棒優化方法刻畫問題(UMP)的魯棒逼近擬Pareto弱有效解的必要和充分最優性條件. 首先引入問題(UMP)的魯棒對應模型:

然后通過引入一類新的廣義凸性假設條件并借助文獻[12]引入的魯棒型次微分約束規格分別刻畫問題(UMP)的魯棒逼近擬Pareto弱有效解的必要和充分最優性條件,所得結果推廣并改進了已有文獻的結果.

1 預備知識

(T)∶={μT=(μt)t∈T|μt=0,t∈T,僅有有限個μt≠0};

設φ:n→為實值函數,若對任意的x∈n,存在正數L及x的開鄰域N(x),使得對任意的y,z∈N(x),均有|φ(y)-φ(z)|≤L‖y-z‖,則稱函數φ為局部Lipschitz函數. 對任意的d∈n,局部Lipschitz函數φ在x∈n處單邊方向導數定義為

φ在x∈n處關于方向d∈n的Clarke方向導數定義為

若對任意的d∈n,φ′(x,d)存在,且φ′(x,d)=φc(x,d),則稱φ在x∈n處為正則的.φ在x∈n處的Clarke次微分?cφ(x)定義為

?cφ(x)∶={ξ∈n|φc(x,d)≥〈ξ,d〉,?d∈n}.

顯然,若φ為凸函數,則Clarke次微分?cφ(x)退化為經典的凸次微分,即

關于Lipschitz函數的其他概念和性質可參見文獻[13].

定義1[13]設D?n是非空子集,x∈D,則集合D在x處Clarke法錐定義為

Nc(D,x)∶={ξ∈n|〈ξ,v〉≤0,?v∈TD(x)},

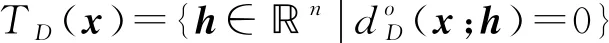
注1[13]顯然,若D?n是非空凸子集,x∈D,則Clarke法錐Nc(D,x)退化為凸分析中經典的法錐N(D,x),即N(D,x)∶={ξ∈n|〈ξ,y-x〉≤0,?y∈D}.

命題1[13]設D?n是非空子集,x∈D. 若φ:n→在x處是局部Lipschitz的,且φ在x∈D處取得最小值,則0∈?cφ(x)+Nc(D,x).

命題2[13]若函數φi:n→(i=1,2,…,m)在n處是局部Lipschitz的,則

命題3[13]若函數φi:n→(i=1,2,…,m)在n處是局部Lipschitz的,則函數在n處是局部Lipschitz的,且

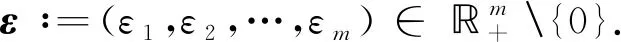
定義2問題(UMP)的魯棒可行集定義為F∶={x∈n|gt(x,vt)≤0,vt∈Vt,t∈T}.

注2若不確定集Ui(i=1,2,…,m)和Vt(t∈T)均為單點集,則問題(UMP)的魯棒可行集退化為問題(MP)的可行集,即F0∶={x∈n|gt(x)≤0,t∈T}.

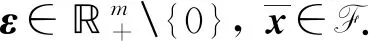
1) 若不存在x∈F,使得

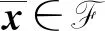
2) 若不存在x∈F,使得

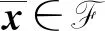
注31) 若定義3中2)的不確定集合Ui(i=1,2,…,m)為單點集,且T為有限集,則問題(UMP)的魯棒Pareto弱有效解退化為文獻[7]中定義1.1的魯棒弱有效解.

2) 若問題(UMP)的目標函數為實值函數,即m=1,則其魯棒ε-擬Pareto弱有效解退化為文獻[12]中單目標半無限優化問題(P)的魯棒ε-擬最優解.

3) 類似地,本文也可引入問題(UMP)的其他魯棒逼近擬Pareto有效解,如魯棒逼近擬Pareto真有效解. 因為其他類型的魯棒有效解可類似處理,故本文僅研究問題(UMP)的魯棒ε-擬Pareto弱有效解.

2 魯棒ε-擬Pareto弱有效解的必要最優性條件

參考文獻[12]引入的一類魯棒型次微分約束規格及合理的假設條件,下面建立問題(UMP)的魯棒ε-擬Pareto弱有效解的必要最優性條件.

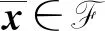
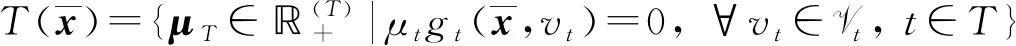
不失一般性,本文假設問題(UMP)的目標函數fi:n×m→(i=1,2,…,m)滿足如下假設條件[14]:

(H1) 對任意的(x,ui)∈n×Ui(i=1,2,…,m),fi(x,ui)是上半連續的;

(H2) 對任意的ui∈Ui(i=1,2,…,m),函數x∈nfi(x,ui)是局部Lipschitz的,并且是正則的;

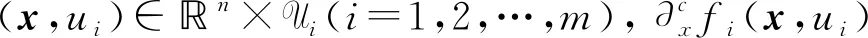
命題4[14]設函數fi:n×m→(i=1,2,…,m)滿足假設條件(H1)～(H3),Ui(i=1,2,…,m)是m上的緊凸集,且fi(x,·)在Ui上是凹函數. 則對任意的x∈n,有

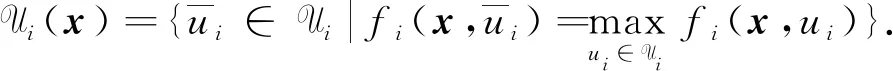
為簡單,記λ∶=(λ1,λ2,…,λm)∈m.

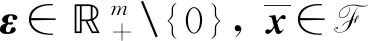
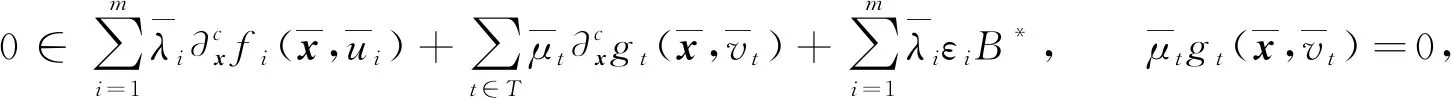
(1)

(2)

證明: 對任意的x∈F,記函數

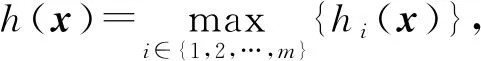
從而

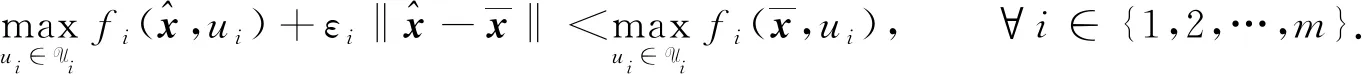
(3)

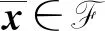
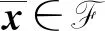
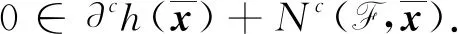
(4)

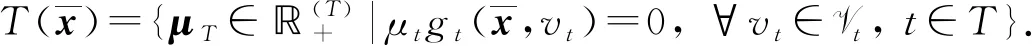
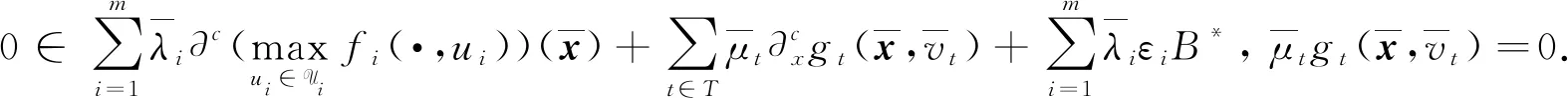
(5)

又由命題4可知

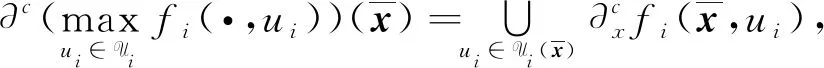
(6)

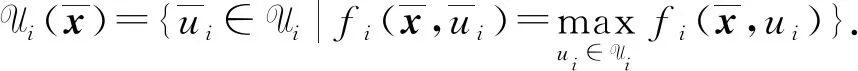
定理1刻畫了問題(UMP)的魯棒ε-擬Pareto弱有效解的必要條件.

若ε=(0,0,…,0),則有如下關于問題(UMP)的魯棒Pareto弱有效解的必要最優性條件.

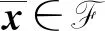
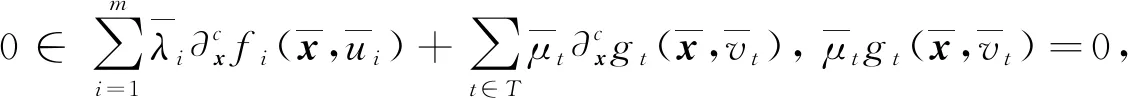
(7)

(8)

3 廣義凸性假設與充分逼近最優性條件

下面借助一類新的廣義凸性假設條件,給出問題(UMP)的魯棒ε-擬Pareto弱有效解的充分最優性條件. 為簡單,記f∶=(f1,f2,…,fm),g∶=(g1,g2,…,gt).

受文獻[7-8]啟發,先引入下列ε-偽擬廣義凸性的假設條件.

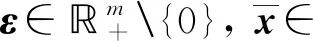
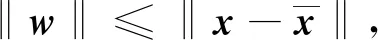
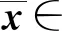
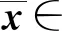
下述定理給出了問題(UMP)的魯棒ε-擬Pareto弱有效解的一類充分最優性條件.

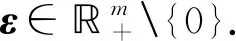
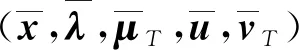
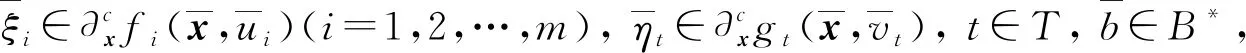
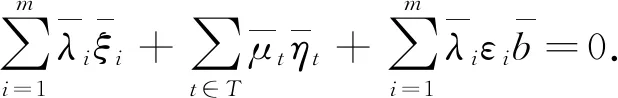
(9)

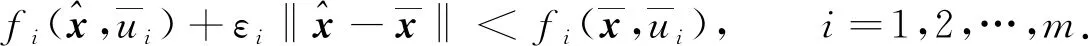
(10)

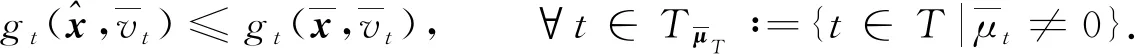
(11)

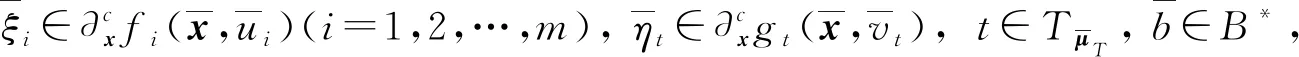
從而

若ε=(0,0,…,0),則有如下關于問題(UMP)的魯棒Pareto弱有效解的充分最優性條件.

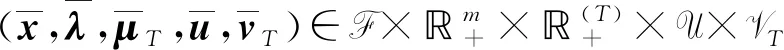
綜上所述,本文從魯棒優化的角度出發,借助一類新的魯棒型次微分約束規格和廣義凸性假設,研究了一類目標函數和約束函數均帶有不確定信息的非凸非光滑半無限多目標魯棒逼近擬Pareto弱有效解的最優性條件. 所得結果可為解決實際問題中不確定優化模型提供一定的理論參考.