一類參數曲線的積累平均弧長參數化方法*
賀詩濤,申立勇
(中國科學院大學 數學科學學院,北京 100049)
*“第23屆計算機輔助設計與圖形學學術會議(CAD&CG 2020)”推薦論文.
計算機輔助幾何設計(簡稱CAGD)[1]利用計算機強大的計算能力解決幾何設計問題,研究自由型曲線曲面. 而找到既適合計算機處理,又能有效滿足形狀表示與幾何設計要求,且便于形狀信息傳遞和產品數據交換形狀描述的數學方法,是CAGD的核心問題. 為清楚表達自由型曲線曲面,Ferguson[2]率先將參數多項式引入了CAGD. Schoenberg[3]提出了樣條函數[4-5]用以解決連接問題,但曲線曲面形狀控制的難題仍待解決. Bézier方法[6]更強調幾何直觀,并在解決整體形狀控制方面有重大突破,但仍存在連接問題和局部修改問題. B樣條方法[7-15]在保留Bézier方法優點的基礎上成功解決了局部控制問題和參數連續性的連接問題,但在處理圓錐曲線和初等解析曲面時只能給出通常不合要求的近似表示. 為解決該問題,Forrest[16]先給出了有理Bézier形式的圓錐曲線,之后Versprille[17]提出了有理B樣條方法. 非均勻有理B樣條(簡稱NURBS)方法將有理與非有理Bézier曲線曲面、有理與非有理B樣條相統一,不僅保留了非有理B樣條的優點,還具有精確表達二次曲線曲面的功能. Sederberg等[18-19]提出了T樣條方法,對B樣條曲面進行了改進.
參數化在CAGD中具有重要作用. 設計者希望使用的參數化方法能盡量反應被插曲線或用數據點所構造曲線的性質. 此外,當給定控制頂點生成一條k次非均勻B樣條曲線時,由于通常節點矢量未知,因此還需確定節點矢量中具體的節點值,同樣要求參數化方法. 目前常用的參數化方法有均勻參數化、弦長參數化、向心參數化[20]和福利參數化. 本文提出積累平均弧長參數化法的一般框架,基于局部參數二次多項式插值和光順性的約束準則,給出3種具體的積累平均弧長參數化法,并通過實例說明在給定約束準則進行局部插值后,其所賦予局部插值曲線的性質可從局部傳遞到整體,使得全局插值曲線在同一約束準則下的目標函數值小于弦長參數化和向心參數化的目標函數值.
1 理論框架
積累平均弧長參數化法可視為對弦長參數化的一個改進,將以直代曲的方法改進為以曲代曲,從而增加了一定的自由度,需要約束條件確定局部參數值. 約束條件不同使得積累平均弧長參數化法也不同. 這一特點使積累平均弧長參數化法靈活性較強,可根據實際需求自主選擇相鄰兩點間曲線弧的構造方法,而目前已有的4種參數化方法都沒有該特性. 一般地,對于平面上n個互異數據點Pi(xi,yi)(i=0,1,2,…,n),積累平均弧長參數化方法步驟如下:
1) 確定局部參數多項式插值曲線的次數m;
2) 選取合適的約束條件,以l個點為一組計算出數據點的局部參數和局部插值曲線在相鄰兩點間的弧長,即按P0,P1,…,Pl-1;P1,P2,…,Pl; …;Pn-l+1,Pn-l+2,…,Pn的順序討論,l由m和約束條件確定;
3) 根據局部插值曲線在相鄰兩點間弧長的平均值計算全局參數.
由上述步驟可知,當插值點較多時,該理論框架對應的問題是一個多參數非線性優化問題,一般方法求解該類問題的效率較低. 因此本文應用局部傳遞到整體的思路,給出一種基于局部求解,然后逐步積累弧長均值的方法. 先不斷利用局部插值求出局部最優解,得到局部參數,然后將相鄰兩點間全部弧長的均值進行累積以求得全局參數,將此作為全局最優解的一個近似. 由實例計算可見,該近似解能使得全局插值曲線由約束條件決定的目標函數值小于傳統參數化方法,如弦長參數化和向心參數化所對應的目標函數值,表明本文算法有效. 由于參數二次多項式曲線非常簡單,因此本文給出的3種具體的積累平均弧長參數化法都基于局部參數二次多項式插值,區別在于約束條件的選取.
1.1 三點二次插值長度最短約束
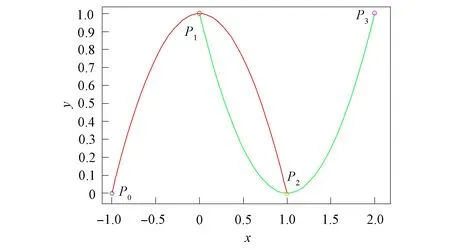
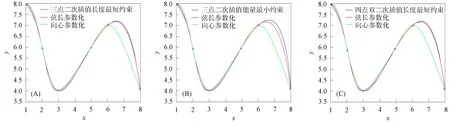
設平面上有3個互異數據點Pi(xi,yi)(i=0,1,2),過上述3點構造參數二次多項式插值曲線P,設其局部參數分別為0,u1,1,其中0 (1) 將式(1)寫成分量形式為 (2) (3) 記 則可將式(2)和式(3)簡化為 x=Au2+Bu+x0, (4) y=Cu2+Du+y0. (5) 由于u1是變量,當其取值在0~1區間變化時,二次參數多項式插值曲線P也會發生變化,因此為確定取值,需要一個約束. 在實際應用中,通常會遇到符合要求的曲線不唯一的情形. 為找到一條最符合要求的曲線,需給出一些約束準則. 考慮到波動劇烈的曲線通常相對較長,因此為選擇波動小、更平直的曲線,可從曲線長度最短出發構造約束準則. 基于此,可令u1的取值使參數二次多項式插值曲線的目標函數值最小,目標函數為 為討論方便,記被積函數為 (6) Q1=(2Au+B)2+(2Cu+D)2. 易見E1是以u1為自變量的一元函數. 求使E1達到最小的u1值,即為求E1的最小值點. 根據給定的約束準則,對Pi,Pi+1,Pi+2三點作局部參數二次插值并求出目標函數E后,可用如下算法計算: 步驟1) 在(0,1)上使用遺傳算法(GA),求出最小值Emin; 步驟4) 若Eval1=Emin,Eval2>Emin,則ui+1=ua,并輸出ui+1; 若Eval1>Emin,Eval2=Emin,則ui+1=ub,并輸出ui+1; 若Eval1=Emin,Eval2=Emin,則: 最小值點的存在性可由物理背景說明,當最小值點不唯一時,可選取離估計值最近的一定精度的最小值點. 從而求得給定精度的最小值點,即u1的局部參數. 根據局部參數利用積累平均弧長參數化法求出其全局參數. 設Pi的全局參數為ti(i=0,1,2),則 t0=0,t1=t0+l1,t2=t1+l2, 其中l1,l2分別表示參數二次多項式插值曲線P在點P0與P1、P1與P2間的弧長,即 下面考慮平面上有4個數據點的情形. 設平面上有4個互異數據點Pi(xi,yi)(i=0,1,2,3),過點P0,P1,P2做參數二次多項式插值曲線Pa,記為Pa(xa,ya). 設P0,P1,P2的局部參數分別為0,u1,1,其中0 (7) 仿照三點情形求u1的值. 根據弧長公式分別計算Pa夾在P0和P1間的弧長l1及P1和P2間的弧長l21. 對于后三點,仿照前面的討論重復操作. 過點P1,P2,P3做參數二次多項式插值曲線Pb,記為Pb(xb,yb). 設P1,P2,P3的局部參數分別為0,u2,1,其中0 (8) 易求出u2的值,從而Pb唯一確定. 根據弧長公式分別計算Pb夾在P1和P2間的弧長l22及P2和P3間的弧長l3. 下面根據數據點的局部參數求全局參數. 注意與三點情形相比的不同: 在數據點P1和P2間有兩段參數二次曲線弧,它們通常并不重合,也不會有相等的弧長. 一種方法是舍去其中一段弧,只保留另一段弧,然后完全按照三點的情形計算全局參數,但這兩段弧是用不全相同的3個數據點生成的,它們包含的數據點信息不全相同,如果舍去其中一段弧的弧長,則會浪費一個數據點的信息. 另一種方法是在局部插值過程中,避免相鄰兩點間出現兩段弧,如假設平面上有5個數據點,令Pa插值于數據點P0,P1,P2,而Pb插值于數據點P2,P3,P4,這樣相鄰兩點間總只有一段參數二次曲線弧,但這種方法對數據點的數量有一定要求,只有在數據點個數可表達成2n+3的形式時才能使用,使得該方法有較大的局限性. 因此,需找到一種更合適的方法能同時使用l21和l22,從而不會發生信息丟失的問題,也不會因為數據點的個數問題產生局限性. 最簡單的方法是用l21和l22的算術平均值代替其中某一段弧的長度,從而可得計算數據點全局參數的公式為 (9) 最后考慮平面上(n+1)個數據點的情形,其中n>3,這種情形的做法和四點情形完全相同. 設平面上有(n+1)個互異數據點Pi(xi,yi)(i=0,1,2,…,n). 首先仿照上述方法,利用長度最短的約束準則計算插值于P0,P1,P2的參數二次多項式曲線,并分別計算夾在P0和P1間的弧長l1及P1和P2間的弧長l21;然后對下面的3個相鄰數據點進行相同操作,分別計算夾在P1和P2間的弧長l22及P2和P3間的弧長l3. 以此類推,以相鄰3個數據點為一組,利用長度最短的約束準則計算插值于Pi,Pi+1,Pi+2的參數二次多項式曲線,并分別計算夾在Pi和Pi+1間的弧長li+1,2及Pi+1和Pi+2間的弧長li+2,1,其中i=2,3,…,n-1. 最后利用積累平均弧長的方法計算數據點的全局參數,公式為 (10) 下面給出以能量最小作為約束準則的方法,其來源于樣條的應變能. 在僅改變約束準則的條件下,積累平均弧長參數化法的步驟幾乎與三點二次插值長度最短約束方法完全一致,因此這里只考慮四點情形. 設平面上有4個互異的數據點Pi(xi,yi)(i=0,1,2,3),過點P0,P1,P2做參數二次多項式插值曲線Pa,記為Pa(xa,ya). 設P0,P1,P2的局部參數分別為0,u1,1,其中0 使用能量最小約束準則,令u1的取值使得插值于P0,P1,P2的參數二次多項式插值曲線能量最小,從而求得唯一的插值曲線Pa,目標函數為 其中ka是插值曲線Pa的曲率,ds是弧微分. 將目標函數寫為 根據曲率公式和弧微分公式,可計算得到Q1的表達式為 采用數值積分方法計算E1,然后根據三點二次插值長度最短約束算法計算u1的值. 從而分別計算出Pa夾在P0和P1間的弧長l1及P1和P2間的弧長l21. 對于P1,P2,P3,可類似求出滿足約束準則的u2值,然后根據弧長公式分別計算出Pb夾在P1和P2間的弧長l22及P2和P3間的弧長l3. 于是可得計算數據點全局參數的公式為式(9). 首先考慮四點的情形. 設平面上有4個互異數據點Pi(xi,yi)(i=0,1,2,3),過點P0,P1,P2做參數二次多項式插值曲線Pa. 設P0,P1,P2的局部參數分別為0,u1,1,且滿足0 過點P0,P1,P2做參數二次多項式插值曲線Pb. 設P1,P2,P3的局部參數分別為0,u2,1,且滿足0 (11) 由于式(11)等號右邊的兩個積分都是非負的,因此可知E取最小值時,這兩個積分分別取最小值. 利用三點二次插值長度最短約束算法分別求出u1和u2的值,即可根據積累平均弧長計算全局參數. 當數據點增多時,可以相鄰四點為一組進行類似討論. 例如,當數據點數為5時,可仿照上述方法得到全局參數的計算公式為 (12) 針對6個及以上互異點的全局參數計算公式為 (13) 與三點二次插值方法相比,四點雙二次插值改變了相鄰兩點間局部插值曲線段的數量,從而在表達式上呈現出加權平均的形式,即得到了與三點二次插值方法不同的全局參數. (A) 弦長參數化,向心參數化,三點二次插值長度最短約束; (B) 弦長參數化,向心參數化,三點二次插值能量最小約束;(C) 弦長參數化,向心參數化,四點雙二次插值長度最短約束.圖1 例1中點在不同參數化和約束條件下的多項式插值曲線Fig.1 Polynomial interpolation curves of points in example 1 under different parameterizations and constraints 下面通過實例計算將上述3種具體的積累平均弧長參數化法與弦長參數化法、向心參數化法進行比較,以說明新參數化方法的優勢. 例1設平面上有4個數據點:P0(1,6),P1(2,4),P2(2.5,3.5),P3(5,8). 做插值于這4個點的參數多項式曲線,結果如圖1所示. 由圖1可見,長度最短約束的積累平均弧長參數化曲線與弦長參數化曲線相近. 長度最短約束的目標函數并非弧長公式,從而導致雖然向心參數化的曲線弧長最短,但在此約束準則下目標函數值最大. 在給定約束準則進行局部插值后,其賦予局部插值曲線的性質可從局部傳遞到整體,使得全局插值曲線在同一約束準則下的目標函數值小于弦長參數化和向心參數化的目標函數值,對比結果如下:對例1中的點分別進行弦長參數化、向心參數化及三點二次插值長度最短約束下的積累平均弧長參數化法所得長度最短約束目標函數值分別為14.352,20.144,13.997;對例1中的點分別進行弦長參數化、向心參數化及三點二次插值能量最小約束下的積累平均弧長參數化法所得能量最小約束目標函數值分別為1.738,3.922,1.616;對例1中的點分別進行弦長參數化、向心參數化及四點雙二次插值長度最短約束下的積累平均弧長參數化法所得長度最短約束目標函數值分別為14.352,20.144,13.997. 由上述對比結果可見,約束準則所賦予的局部性質確實從局部傳遞到了全局插值曲線,在該約束準則下計算出的全局插值曲線的目標函數值與弦長參數化和向心參數化相比有明顯降低. 例2根據如下有序數據點集做參數三次樣條插值曲線: {(1,8),(2,6),(3,4),(5,6),(6,7),(8,4)},結果如圖2所示,圖2中“°”表示數據點. (A) 弦長參數化,向心參數化,三點二次插值長度最短約束; (B) 弦長參數化,向心參數化,三點二次插值能量最小約束;(C) 弦長參數化,向心參數化,四點雙二次插值長度最短約束.圖2 例2中點在不同參數化和約束條件下的多項式插值曲線Fig.2 Polynomial interpolation curves of points in example 2 under different parameterizations and constraints 由圖2可見,目標函數值小的性質仍可由局部傳遞到整體,對比結果如下:對例2中的點分別進行弦長參數化、向心參數化及三點二次插值長度最短約束下積累平均弧長參數化法所得長度最短約束目標函數值分別為15.704,23.929,7.821;對例2中的點分別進行弦長參數化、向心參數化及三點二次插值能量最小約束下的積累平均弧長參數化法所得能量最小約束目標函數值分別為7.085,50.689,5.932;對例2中的點分別進行弦長參數化、向心參數化及四點雙二次插值長度最短約束下積累平均弧長參數化法所得長度最短約束目標函數值分別為15.704,23.929,8.763. 例3根據如下有序數據點集做參數三次樣條插值曲線: {(0,10),(2,10),(3,10),(5,10),(6,10),(8,10),(9,10.5),(11,15),(12,50),(14,60),(15,85)},結果如圖3所示,圖3中“°”表示數據點. (A) 弦長參數化,向心參數化,三點二次插值長度最短約束; (B) 弦長參數化,向心參數化,三點二次插值能量最小約束;(C) 弦長參數化,向心參數化,四點雙二次插值長度最短約束.圖3 例3中點在不同參數化和約束條件下的多項式插值曲線Fig.3 Polynomial interpolation curves of points in example 3 under different parameterizations and constraints 由圖3可見,3種積累平均弧長參數化法生成的插值曲線都與弦長參數化法生成的插值曲線幾乎重合,但目標函數值卻有較大差異,對比結果如下:對例3中的點分別進行弦長參數化、向心參數化及三點二次插值長度最短約束下的積累平均弧長參數化法所得長度最短約束目標函數值分別為85.479,419.640,26.606;對例3中的點分別進行弦長參數化、向心參數化及三點二次插值能量最小約束下的積累平均弧長參數化法所得能量最小約束目標函數值分別為3 915.396,1 166.199,42.341;對例3中的點分別進行弦長參數化、向心參數化及四點雙二次插值長度最短約束下的積累平均弧長參數化法所得長度最短約束目標函數值分別為的85.479,419.640,26.607. 與傳統的參數化方法相比,積累平均弧長參數化法通過局部二次插值引入了額外的自由度,可利用約束準則或其他方法賦予局部插值曲線某種性質,從而使局部插值曲線的性質傳遞到全局插值曲線上. 這種方法可以使設計者根據需求設計參數化方法,并得到具有所需性質的全局插值曲線. 而無論是弦長參數化還是向心參數化方法均無主動設計的空間,其忽略了不同研究者對插值曲線的性質可能有不同的需求,而自身又無法保證能生成最優的曲線. 本文方法給出了一種解決該問題的思路,但本文目標只把一個性質從局部傳遞到整體而非多個,因此求得的并非全局最優解,而為其一個近似解,該近似解能達到全局插值曲線的目標函數值小于弦長參數化和向心參數化結果的目標. 圖4 質點從P0到P3路徑示意圖Fig.4 Schematic diagram of particle’sroutes from P0 to P3 設平面上有4個數據點,質點從P0出發,依次經過P1,P2,最終到達P3. 將數據點的全局參數視為質點從P0運動到Pi所經過的路程. 此時問題轉化為求質點從Pi運動到Pi+1的路程. 圖4為質點從P0到P3路徑示意圖. 由圖4可見,平面上存在4個互異數據點及一個直角坐標系. 在具體問題中需明確坐標系和數據點的坐標,這里為便于說明,只給出其示意圖,不考慮點在給定坐標系中的具體坐標. 首先,考慮質點從P0運動到P1的路程. 由于質點的實際運動路徑未知,所以需構造一條連接P0和P1的特殊路徑,并用其長度對實際路程進行近似. 弦長參數化中用連接P0和P1線段的長度進行近似,該方法簡單,但實際上質點不能恰好做直線運動,所以誤差相對較大. 考慮用參數二次曲線弧的長度對實際路程進行近似,這種方法不會帶來高次插值的問題及過大的計算量,同時也能體現路徑的彎曲. 注意到質點在到達點P1后將會經過點P2,因此可考慮利用P2構造一條從P0到P1的參數二次多項式曲線弧,并做出某種限制使該弧唯一,即得到了所需的特殊路徑,如圖4中紅色曲線所示. 對于質點從P0運動到P1,質點經過P2這一事件發生于未來,因此本文用質點從P0運動到P1這一段運動的未來信息構造質點從P0運動到P1的一條特殊路徑以及相應的路程. 考慮質點從P1運動到P2的路程. 注意到質點在經過P2后將會到達P3,從而可利用數據點P3,即質點從P1運動到P2這段運動的未來信息構造一條特殊路徑,如圖4中綠色曲線所示. 質點在到達P1前曾經過P0,可利用數據點P0,即質點從P1運動到P2的這段運動的過去信息構造一條特殊路徑,如圖4中紅色曲線所示. 本文可進一步認為局部參數值之間有關聯,即質點的過去運動狀態和未來運動狀態有關聯. 這種思路可用于四點雙二次插值的積累平均弧長參數化法. 于是得到了從P1到P2的兩條特殊路徑. 本文可要求質點沿紅色或綠色的曲線運動,用這段曲線的弧長對P1到P2的實際路程進行近似. 該方法會丟失一個數據點的信息. 從物理角度看,這樣做會丟失質點運動狀態的信息. 為對質點的實際運動路程做更精確的近似,需要更多質點運動狀態的信息. 考慮如下問題: 假設有大量質點從P0出發運動到P1,則有些質點可能會沿紅色路徑運動到P2,而其他質點會沿綠色路徑運動到P2. 即質點從P1運動到P2所選擇的路徑是一個隨機現象,其樣本空間元素個數為2. 而質點從P1運動到P2的路程可視為一個隨機變量,該變量為離散隨機變量,因此可從概率論的角度考慮問題. 當質點選擇紅色、綠色路徑的概率已知時,則可根據兩種顏色的曲線夾在P1,P2間的弧長計算出質點從P1運動到P2的路程的期望,將其作為質點從P1運動到P2的實際路程的近似值. 上述分析表明,這兩條路徑的重要程度對質點是相同的,質點選擇兩條路徑中任意一條的概率均為1/2. 于是可計算出質點從P1運動到P2的路程的期望等于兩段弧長的算術平均值. 若質點選擇兩條路徑中任意一條的概率不相等,例如,質點沿路程長的路徑運動的概率小,或質點沿能量大的路徑運動的概率小. 則此時從表達式上看,應對相鄰兩點間的全體曲線弧的長度計算加權平均,而非算術平均. 質點從P2運動到P3的討論類似于從P0運動到P1,差異在于后者以P0為起點,在其之前并無數據點,即無法使用質點過去運動狀態的信息; 前者以P3為終點,在其后無數據點,即無法使用質點未來運動狀態的信息. 從物理的角度看,這3種方法在思想上沒有本質區別,針對于不同的需求提出不同的約束需求,例如,數控機床(CNC)軌跡規劃中在本文的能量最小約束下可具有更好的加工進給速度. 此外,對于其他數據點個數的情形,物理解釋也相同. 對于計算不位于兩端的數據點的全局參數,關鍵是首先構造多條特殊路徑,然后計算弧長平均值或路程期望,用其對實際弧長或路程進行近似. 綜上所述,本文給出的3種積累平均弧長參數化方法都按積累平均弧長參數化法的一般框架給出,無論是參數多項式插值還是參數三次樣條插值,均可得到在所選約束準則下比弦長參數化和向心參數化目標函數值更小的結果. 本文只對低次參數多項式插值和參數三次樣條插值在不同參數化方法下求得的目標函數值進行了對比. 本文給出的參數化方法雖在算例中可使目標函數值小于弦長參數化和向心參數化的結果,但也存在一些示例使得積累平均弧長參數化法計算得到的目標函數值大于弦長參數化或向心參數化的結果. 對這些示例進行計算表明,積累平均弧長參數化給出的全局參數較接近弦長參數化給出的參數,并且由于前者給出的全局參數總不小于后者在對應點給出的參數,使得前者得到的全局參數可被視為對后者的一個參數增加的擾動. 若積累平均弧長參數化給出的目標函數值與幾種方法中目標函數最小值相差較小,則可從數值誤差方面進行分析.
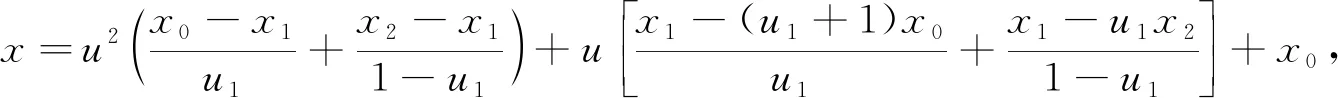



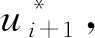


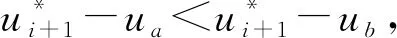


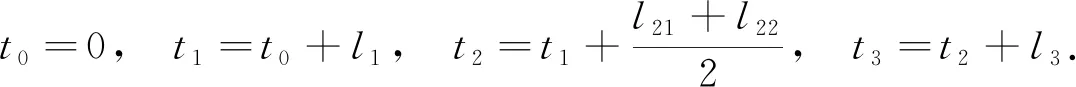
1.2 三點二次插值能量最小約束
1.3 四點雙二次插值長度最短約束



2 實例計算

3 物理解釋