微振動主動隔振系統的研究綜述*

易思成,王金海,劉志剛,張 泉,楊斌堂,孟 光

(1.上海大學 機電工程與自動化學院，上海 200444；2.上海交通大學 機械系統與振動國家重點實驗室，上海 200240；3.上海航天控制技術研究所，上海 201109)

0 引 言

精密加工和測量、空間遙感和觀測等技術的發展對機械裝置的精度提出了更高的要求，一般需要達到微納尺度。然而，外部環境或者裝置內部的微幅振動會造成超精密機床[1]、坐標測量儀[2]、光學顯微鏡[3]等儀器的精密度和準確度嚴重下降。在航天器上，斯特林制冷機、反作用飛輪、太陽能帆板的驅動機構等裝置容易產生隨機和諧波擾動，影響在軌運行航天器的定位和指向精度。對此，應該采用主動或者被動振動控制方法，盡可能消除或隔離機械系統外在與內在的各種干擾，使系統高效穩定地運行，以增強機械系統對微振動的抗干擾能力[4]。

和其他主動控制系統類似，主動隔振系統由被控對象、驅動器、控制器等環節等組成，各環節相互關聯，共同決定了系統的執行精度和運動特性。因此，有必要全面總結和分析主動隔振系統關鍵組成部分的研究成果，為研制新型高精密隔振系統提供理論依據和設計指導。

當前，研究人員越來越多地采用智能材料驅動器(典型的有壓電和磁致伸縮式)作為微振動隔振系統的執行單元。然而，智能材料的遲滯給隔振系統的控制和實現帶來了挑戰，如何對微振動隔振系統的遲滯進行表征和控制成為當前的研究熱點。

筆者在微振動隔離系統的設計和實現、遲滯系統的建模和補償等方面積累了一些理論基礎和技術方法，并取得了一定的研究成果[5-8]。基于上述經驗和國內外最新研究成果，本文圍繞微振動隔離標準、隔振系統的構型設計、驅動器的選擇與設計、系統模型的建立、振動主動控制方法等內容對微振動主動隔振領域的研究進行綜述，并預測該領域的發展趨勢。

1 微振動及其隔離標準

微振動通常指的是頻率集中在1 Hz～1 kHz的微米或者亞微米幅度的機械振動或者干擾[9]。不同性能和用途的精密儀器對所允許干擾的幅度和帶寬不同，需要設定一套標準評價微振動隔離是否有效。

精密儀器所允許的振源速度標準如圖1所示。

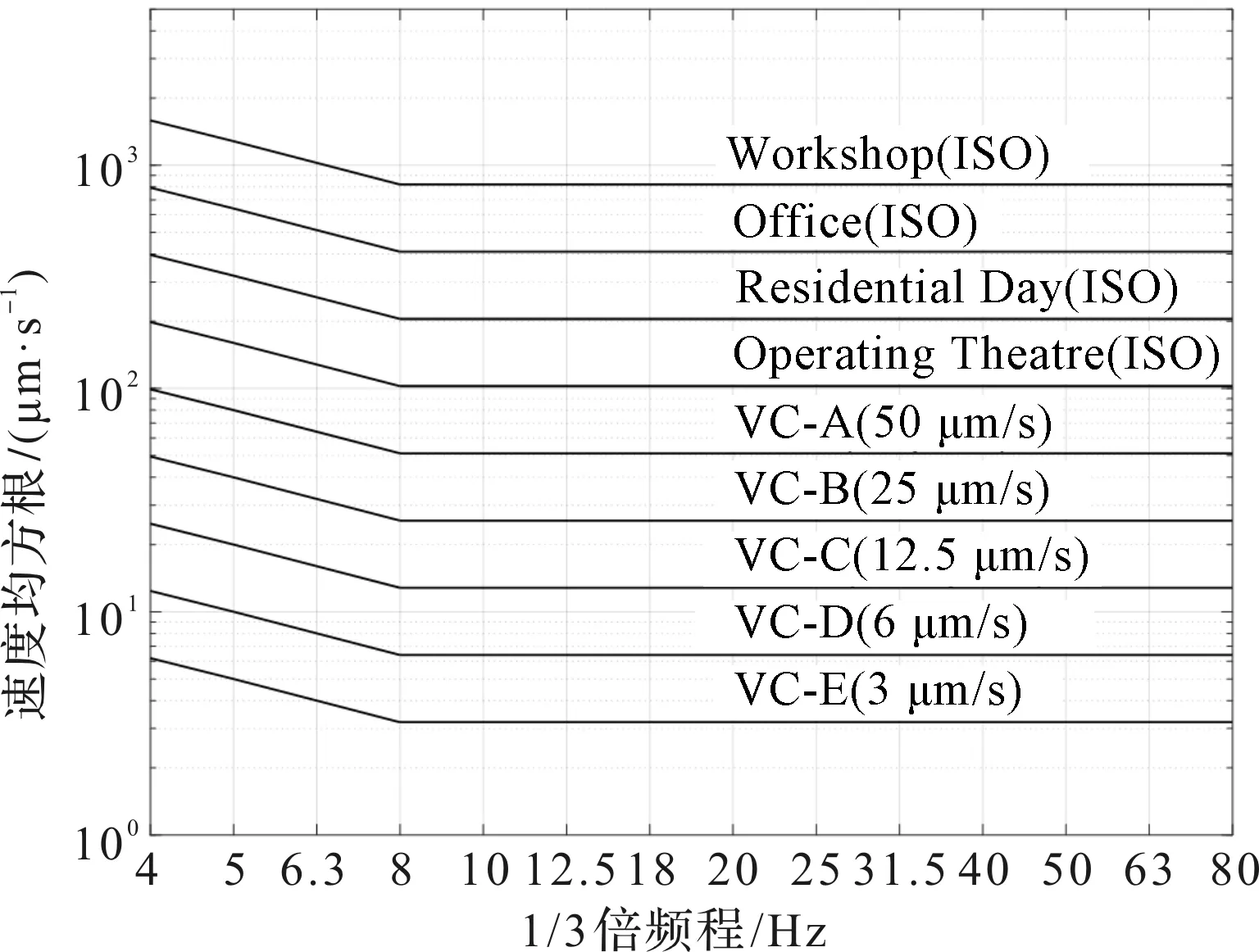
圖1 精密儀器所允許的振源速度標準曲線

由圖1可知：在ISO (international standards organization)準則的基礎上引入振動標準曲線(vibration criterion, VC)，描述一定帶寬范圍內不同工況下微振動允許值，圖的橫軸為三分之一倍頻程，縱軸為速度均方根[10]；從VC-A到VC-E準則，振動允許值越來越小，其中VC-A準則應用于光學顯微鏡，而VC-E準則適用于長距離、微小目標的激光跟蹤定位系統。

2 隔振系統的構型設計

2.1 單軸隔振系統

單軸隔振系統可用于抑制單方向的微振動干擾，主要分為直接主動式和主被動一體式。直接主動式的基本原理是利用驅動器產生的作動力抵消微振動源引起的干擾力[11,12]。

主被動一體微振動隔振系統的原理簡圖以及頻域內振動傳遞率曲線[13]如圖2所示。

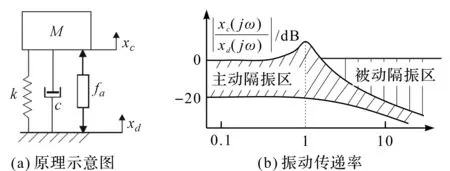
圖2 單軸隔振系統及振動傳遞率c—被動阻尼；k—被動剛度；fa—主動力

其中：被動剛度用于抑制中高頻振動干擾，主動力用于隔離低頻振動干擾[14-16]。

2.2 多軸隔振系統

為解決多維微振動干擾的問題，研究人員開發了能實現空間多維運動的多軸隔振系統。平臺大多基于并聯結構[17]。在多個驅動器的共同作用下，傳遞到負載平臺的多維干擾能被隔離。例如3軸微振動隔離平臺用于隔離兩個轉動和一個平動干擾[18]，或者3個移動干擾[19]；6軸微振動隔離平臺用于隔離空間任意方向的干擾，最為典型的是“立方體”構型的Stewart隔振系統。

Stewart的示意圖及幾何構型如圖3所示。

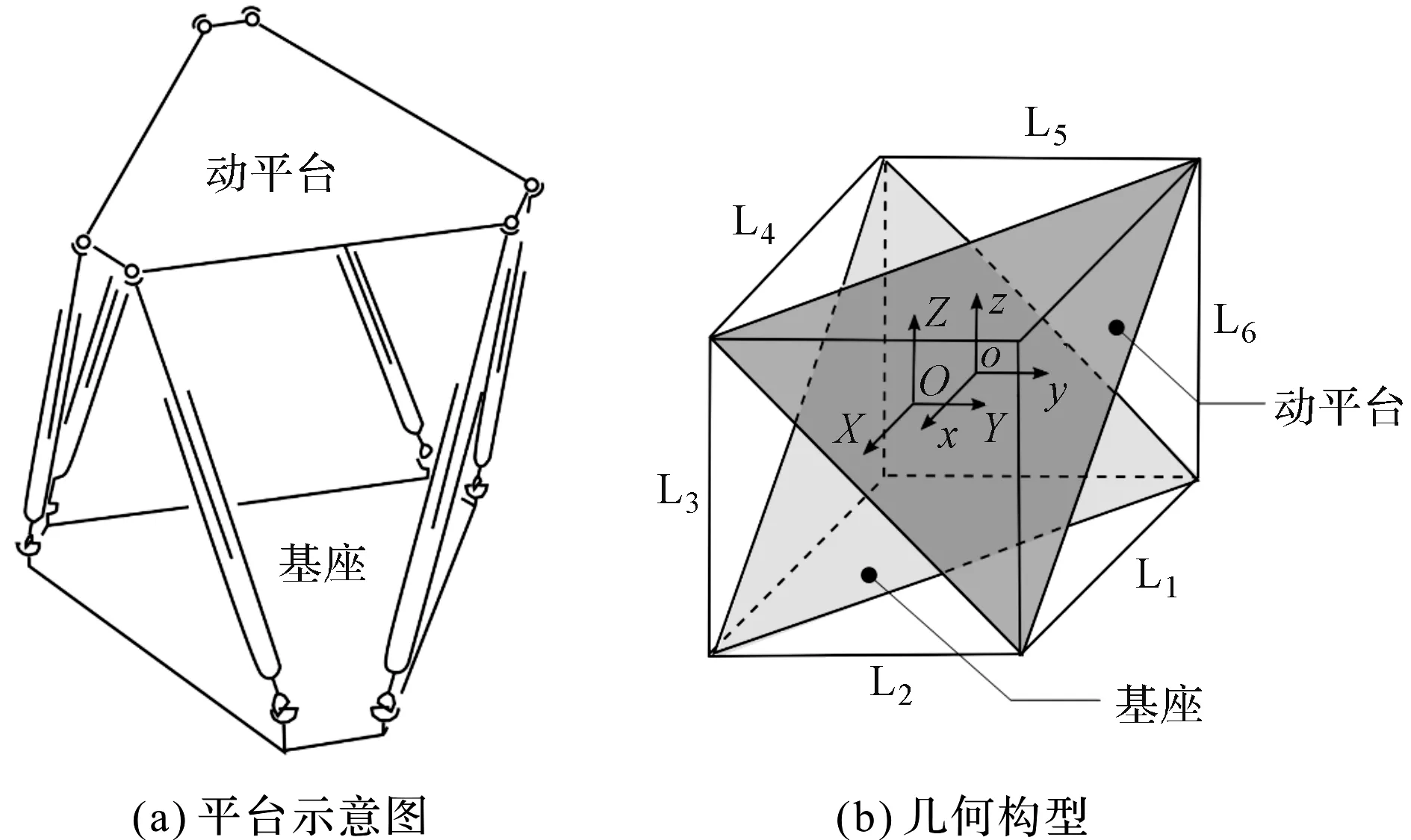
圖3 立方體構型Stewart平臺

該平臺由6個驅動器組成，整體結構緊湊，輸出精度高、承載能力強、動態特性好[20]。

ABU等[21]設計的Stewart隔振平臺如圖4所示。

圖4 ABU等設計的Stewart隔振平臺

該平臺的每條支鏈由1個音圈電機和1個力傳感器組成，12個加速度傳感器分兩組布置在基座和動平臺上。

3 驅動器的設計與選擇

盡管利用具有高精密性能的傳統驅動器(如液壓、氣壓或者電磁式)可以實現微振動干擾的控制，然而傳統驅動裝置復雜的結構限制了其廣泛的應用。隨著材料、生物、化學等學科和機械學科的交叉發展，基于智能材料的微振動隔振系統已成為當前技術研究的熱點。典型的智能材料有壓電、超磁致伸縮、記憶合金、磁流變/電流變、高分子聚合物等。智能材料驅動器能夠克服傳統驅動器結構中間隙、摩擦、磨損等的不利影響，提升系統的精度、可靠性和響應速度。

下面主要對靜電、電磁、壓電、超磁致伸縮、高分子聚合物驅動器在微振動隔振領域的應用進行闡述：

(1)靜電

為解決陀螺儀對外界高頻振動敏感的問題，DEAN等[22]在平行靜電極板的基礎上開發了結構精巧、驅動傳感集成度高的陀螺儀隔振裝置。該隔振裝置集成了靜電式速度傳感器、靜電驅動器和反饋電路。無反饋控制時，隔振裝置的品質因子為150 dB；而應用反饋控制后，隔振裝置的品質因子減小到60 dB。

(2)電磁

電磁式驅動器的輸出力是交變磁場中線圈和永磁體相互作用產生的洛倫茲力。電磁驅動器在振動控制領域有著廣泛的應用，其優點在于成本低、帶寬大、容易控制。音圈電機(voice coil actuator，VCA)是一種特殊形式的電磁式驅動器，具有結構簡單、體積小、響應快等優點。PREUMONT[23]研制了行程為±0.7 mm的音圈電機式微振動隔振系統。在音圈電機中，有一類剛度小、能有效隔離高頻微振動干擾的“軟驅動器”。在Honeywell公司研制的振動隔離和抑制系統(vibration isolation and suppression system，VISS)，其音圈驅動器的截止頻率低至1 Hz[24]。磁懸浮隔振是一種比較新穎的電磁式隔振方法，具有可靠性高、使用壽命長等優點。HOQUE等[25]在傳統隔振系統中引入磁懸浮隔振技術，采用主動控制策略實時調節磁懸浮的懸浮力。

(3)壓電

壓電驅動器具有響應快、輸出精度高、易加工等優點[26]。PETITJEAN等[27]設計了由壓電驅動器、力傳感器和被動隔振單元組成的主被動一體式單自由度隔振系統。為解決航天器有效載荷的振動控制問題，VAILLON等[28]介紹了一種壓電疊堆式的主動隔振單元，實驗結果表明：利用該隔振單元，由動量輪產生的諧波微振動干擾減小了30 dB～40 dB。為隔離較大幅值的微振動干擾，BADEL等[29]設計了帶有放大機構的壓電驅動器，并提出了遲滯補償和PI反饋復合控制方法。GARCIABONITO等[30]設計了一種用于振動控制的帶有液壓放大機構的壓電驅動器。

(4)超磁致伸縮

超磁致伸縮材料(giant magnetostrictive material, GMM)在外加磁場作用下會產生應變和應力，例如含有稀土元素Terfenol-D合金的磁致伸縮系數可達1 500×10-6到2 000×10-6，其最大伸縮量是常規磁致伸縮材料的數十倍。ZHANG等[31]依據啄木鳥頭部結構設計了仿生式主動隔振系統，該系統由大功率磁致伸縮驅動器、空氣彈簧、基座以及橡膠層等組成。

需要說明的是，由于音圈電機、壓電驅動器和磁致伸縮驅動器的結構緊湊，它們一般被用作多自由度微振動隔振系統的主動單元。

(5)高分子聚合物

聚合物又稱高分子化合物，是一類能將光、電或磁等物理能轉換為機械能的新型智能材料，常見的有介電彈性體和壓電聚合物。介電彈性體(dielectric elastomer, DE)是電活性聚合物的一種，其優點在于應變大、能量密度高、效率高、響應快且加工制造方便等。SARBAN等[32]詳細描述了管狀介電彈性體驅動器的研制過程，設計了自適應前饋控制器，并將其用于微振動控制。實驗結果表明：利用該方法，可使5 Hz和10 Hz的單頻微振動干擾能分別減小66 dB和23 dB。

(6)驅動器的性能比較

雖然驅動器的形態多樣、原理不同，但可利用一些性能指標來衡量和評估它們的使用性能。歸納起來，這些指標大致分為3類：幾何和物理參數(如運動形式、體積、質量等)、靜態參數(如行程、最大驅動力、剛度、精度、效率等)、動態參數(如固有頻率、帶寬、被動阻尼等)。根據任務需求和應用場合的不同，設計或選用符合要求的驅動器是研制主動微振動隔振系統的重要環節。

在主動隔振系統中，驅動器輸出性能需要滿足的必要條件是其作動行程必須大于等于外界微振動激勵的位移[33]。

典型驅動器的行程和最大輸出力如圖5所示。

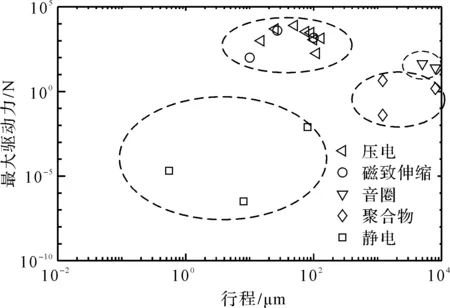
圖5 驅動器的靜態輸出特性比較

圖5中包括壓電驅動器[34,35]、磁致伸縮驅動器、音圈電機[36,37]、高分子聚合物[38]、靜電驅動器[39,40]。由圖5可知：壓電驅動器和超磁致伸縮驅動器可用于抑制大負載的低幅振動；音圈電機能隔離幅度較大的振動并具有較強的帶載能力；靜電驅動器的輸出功率較?。唤殡姀椥泽w驅動器能對幅度較大的微振動進行抑制，但靜態輸出力不大。

除了行程和最大輸出力等靜態性能外，隔振系統自身的固有頻率也是重點分析的對象。一般而言，壓電和超磁致伸縮驅動器的固有頻率較高，而電磁、靜電和介電彈性體驅動器的固有頻率適中。

4 系統模型的建立

4.1 結構動力學建模

一般利用集中參數模型對隔振系統進行描述，該模型由集中質量、集中剛度和集中阻尼組成，分布載荷等效在集中質量上。有限元模型也是隔振系統的常用建模方法之一，可使用有限元商業軟件對隔振系統進行動力學分析。需要說明的是，有限元模型計算量大，如要進一步應用于主動控制，必須對原始模型進行縮減。

針對集中參數模型或有限元模型，通過動力學建模方法可得到系統的動力學模型[41]。常見的動力學建模方法如圖6所示。

圖6 動力學建模方法

LIU等[42]根據牛頓-歐拉法建立了8支鏈隔振系統的動力學模型，并在此基礎上分析了系統的結構參數對動力學響應的影響。

振動傳遞率是微振動隔振系統重要的性能評價指標，其定義為隔振后運動或力的幅值與隔振前的比值，通常表示為頻譜函數。微振動隔離平臺傳遞率的求解方法包括傳遞矩陣法、阻抗法、頻響函數綜合法。PREUMON等[43]利用傳遞矩陣對Stewart隔振平臺的底座和上平臺之間的關系進行了表征，根據Forbenius范數，將多自由度系統的傳遞矩陣等效為單自由度形式的傳遞矩陣，進而求得振動傳遞率。

針對主被動一體的隔振系統，KIM等[44]利用阻抗矩陣定量描述系統的物理特性，接著將阻抗矩陣轉化為狀態方程，為設計反饋控制器提供了理論支持。傳遞函數在微振動主動控制系統設計中應用較為廣泛。YEN等[45]建立了多自由度壓電式主動隔振裝置的傳遞函數，利用解耦策略對傳遞函數矩陣進行了對角化，通過實驗驗證了變換模型的有效性，最后設計了離散式的滑模控制器。

需要說明的是，隔振系統的基座是微振動干擾的直接受體，當基座相對于平臺的柔性較大時，需要將柔性變形引入系統的結構動力學方程[46]。

4.2 驅動器遲滯建模

驅動器是微振動隔振系統中產生力和運動的單元。在對隔振系統的靜態和動態性能進行分析時，應當考慮驅動器的輸出特性。驅動器將其他形式的能量轉化為機械能，因此基于能量的轉換、調控和傳遞的過程，可對驅動器進行多物理場建模。例如，利用靜電能和機械能的轉換對靜電式驅動器進行建模，利用電場能和機械能的轉換對壓電式驅動器進行建模。

接下來，將對智能材料驅動器的建模方法進行歸納和總結。

在小位移條件下，智能材料驅動器的位移輸出可近似認為是線性的，此時可利用材料的線性本構方程建立驅動器的輸入輸出模型。壓電材料和磁致伸縮材料的本構關系具有相似性。KAMESH等[47]利用本構方程建立了集成傳感單元的壓電作動器的多場耦合模型。

雖然基于智能材料的驅動器在主動微振動控制中應用廣泛，但在大變形條件下，材料的遲滯非線性對控制器的設計提出了挑戰。遲滯指的是材料具有記憶性，當輸入作用于系統時，它的輸出表現為一定的滯后。為預測系統輸出或補償遲滯非線性，研究人員對遲滯進行了理論建模，例如物理法、唯象法等，前者根據驅動器的物理機理進行建模，后者根據驅動器輸入輸出的幾何關系進行建模。

常見的遲滯建模方法如圖7所示。

圖7 遲滯建模方法

限于篇幅，文中只對微振動主動控制研究中常用的幾種遲滯建模方法進行綜述：

(1)Jiles-Atherton模型

Jiles-Atherton(J-A)模型主要用于磁致伸縮驅動器的建模。早期的J-A模型是一種基于能量的靜態磁滯模型。后來JILES和SABLIK等學者對該模型進行了擴充和修正，使修正后的模型能夠描述磁化強度和磁致伸縮的耦合效應，極大地擴展了J-A模型的使用范圍[48]。

(2)Bouc-Wen模型

BOUC于1971年首次提出了一種遲滯的半物理建模方法，WEN在1976年對該模型進行了改進，形成了Bouc-Wen模型[49，50]。廣義的Bouc-Wen模型的表達式如下：

(1)

式中：v—遲滯系統的輸入；z—遲滯系統的狀態變量；A,β,α—描述遲滯環的形狀參數。

在壓電驅動器中，通常認為n=1。

ZHANG等[51]將線性本構方程和式(1)所示的Bouc-Wen模型結合，構建了磁致伸縮驅動器的非線性本構模型，并通過實驗證明，利用該模型能有效擬合驅動器的遲滯曲線。

(3)Preisach模型

Preisach模型是一種經典的遲滯算子模型。連續形式的Preisach模型的數學表達式如下：

(2)

式中：u(t)—模型的輸入；y(t)—模型的輸出；γαβ[u(t)]—矩形算子；P(α,β)—權函數；α,β—描述矩形算子形狀的參數。

根據輸入信號方向的不同，矩形算子γαβ的取值為-1或1。PASCO等[52]對比了基于線性本構方程和基于Preisach模型的壓電驅動器的遲滯建模方法，發現后者的建模精度更高。

(4)Prandtl Ishilinskii模型

Prandtl Ishilinskii (PI)模型是由Preisach模型發展而來的，它的基本元素為Play算子(間隙算子)或者Stop算子。Play算子的表達式如下：

(3)

Stop算子的表達式如下：

er[v](t)=

(4)

式中：v(t)—算子的輸入；fr(t)—Play算子的輸出；er(t)—Stop算子的輸出；fr(0)—Play算子的初始輸出；er(0)—Play算子的初始輸出；r—描述算子形狀的參數(也稱為閾值)；t-—當前時間的前一時刻。

Play算子和Stop算子的關系可以表示為：

fr[v](t)+er[v](t)=v(t)

(5)

在分段單調連續輸入函數作用下，基于Play算子的PI模型可以表示為：

(6)

式中：p(r)—密度函數(由實驗測得的系統輸入輸出數據辨識得到)；q—大于零的常數。

當閾值r較大時，PI模型的輸出衰減較快，為方便計算，R通常取為∞。

相比于Preisach算子，PI算子的優點在于結構簡單、逆算子有解析解、便于實時控制。KUHNEN[53]推導并分析了PI算子的逆模型，并通過逆算子的補償實現了磁致伸縮驅動器的精密定位。盡管PI算子有以上優點，但是它無法表征非對稱遲滯環，對此研究人員提出改進的PI算子來解決該問題[54,55]。筆者[56]利用多項式改進的PI模型，對磁致伸縮微振動隔振平臺中的驅動器進行了遲滯建模。

(5)遲滯率相關改進模型

上述提到的物理或者唯象建模方法只對靜態遲滯現象是有效的。當遲滯系統輸入信號的頻率增大時，原有靜態遲滯模型無法描述遲滯系統的動態效應。因此，一些學者對率相關遲滯建模方法進行了研究與探討。

綜上所述，遲滯物理模型對驅動器設計提供了理論依據，但這類模型比較復雜且精度有限。而遲滯唯象模型是以實驗數據為基礎，能較為精確地對驅動器遲滯環的形狀進行描述，同時利用遲滯唯象模型還可設計基于遲滯逆的前饋控制器。

5 振動主動控制方法

微振動主動控制方法包括反饋控制、前饋控制、反饋和前饋結合的復合控制等。針對控制目標(微振動)和控制對象(微振動隔振系統)的特點，研究人員也設計了一些新型控制器。

5.1 反饋控制方法

利用PID控制可抑制微振動干擾引起的系統響應。欲使PID控制效果更優，需增大控制環節的增益，但這會引起控制器失穩。為此，JAENSCH等[57]對隔振系統的機械結構進行了改進，提高了系統運動穩定性，同時探究了高增益(特別是高積分增益)對系統穩定性的影響，為控制器的參數調節提供了理論依據。

在主動微振動控制中，常見的反饋量包括加速度、速度、位移或者力。“天棚阻尼”法是一種行之有效的振動控制方法，其基本原理是利用被隔對象的絕對速度設計微振動反饋控制器。YOSHIOKA等[58]通過位移反饋和絕對速度反饋對6自由度隔振系統進行了控制。

基于力傳感的反饋在微振動控制中應用廣泛[59]，主要原因在于：(1)即使基座或敏感負載存在柔性，利用基于力傳感的反饋控制也能保證隔振系統的穩定性；(2)微重力環境中低頻加速度較難檢測，此時可采用力傳感進行閉環控制。

GENG等[60]利用局部力反饋控制器調節驅動器的等效阻抗，使之與隔振系統的機械阻抗相等，從而最大程度地抑制了微振動干擾。在其他一些應用場合中，載荷的振動對基座的影響也應該予以考慮。HAUGE等[61]對這些影響進行了分析，發現產生該問題的原因是多軸隔振系統的耦合效應，并利用改進的控制器提升了6軸隔振系統的工作性能。

5.2 前饋控制方法

對于反饋控制，構造主動控制律僅需隔振系統的輸出信號。若微振動干擾信號已知且是確定的，那么可以利用該先驗知識設計前饋控制器。由于微振動干擾信號和振動傳遞通道的參數是時變的，在工程應用中，常采用自適應前饋方法補償振動傳遞通道的時變動態。

最為典型的自適應前饋控制器是基于有限脈沖響應(finite impulse responses，FIR)的濾波x最小均方控制器(filtered-x least mean square, FxLMS)[62]。

FxLMS算法的基本框圖如圖8所示。

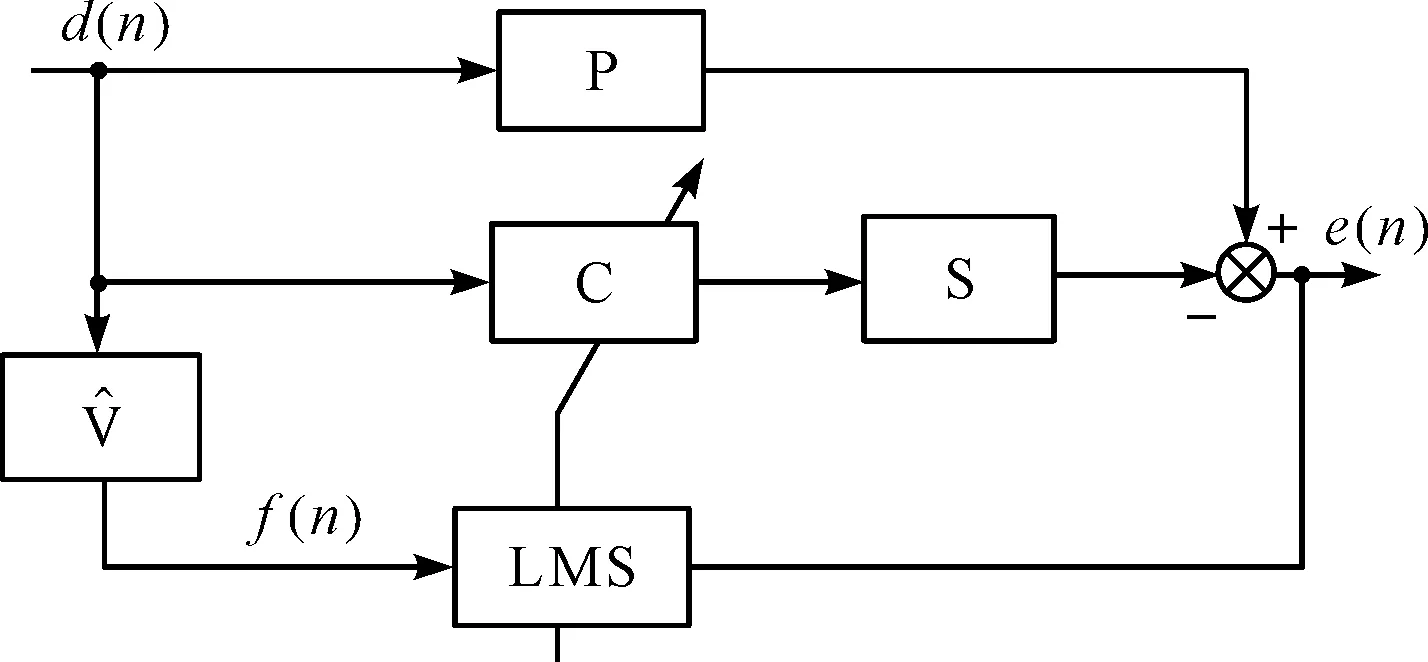
圖8 FxLMS控制算法的框圖P—初級通道；S—次級通道；C—控制器；次級通道的辨識模型；e(n)—隔振系統的輸出信號。其中：用FIR濾波器予以表示。

在此基礎上，也衍生出了一些其他形式的自適應前饋控制器，例如基于無限脈沖響應(Infinite impulse response, IIR)的濾波μ最小均方(filtered-μ least mean square, FuLMS)控制器，基于FIR的濾波最小均方(filtered-least mean square，FLMS)控制器[63]。筆者[64]對傳統的FxNLMS算法進行了改進，依據多項式改進PI模型，對磁致伸縮微振動隔振系統的非對稱遲滯進行了補償控制。

5.3 復合控制方法

反饋控制和前饋控制各有優缺點。為提高微振動隔振系統的性能，研究人員提出了反饋與前饋結合的復合控制方法。

反饋控制和前饋控制的特性比較如表1所示。

表1 振動反饋和前饋控制的比較

筆者[65]利用PI反饋和FIR前饋復合控制對噪聲干擾下的原子力顯微鏡(atomic force microscopy, AFM)的探針振動進行了主動控制，實驗結果表明：控制器能有效減少窄帶和寬帶噪聲導致的AFM掃描圖像的條紋和畸變。WANG等[66]利用力反饋和自適應前饋協同控制對多維微振動進行了主動控制。實驗結果表明：利用自適應前饋控制器能對多頻簡諧干擾進行抑制；而利用基于主動阻尼的力反饋控制器能對有限寬帶內的隨機微振動干擾進行抑制。

5.4 新型控制方法

由于主動隔振系統的模型復雜、具有多個控制目標以及受到外界干擾的影響，在某些情況下，利用傳統控制方法無法實現預期的微振動隔離效果，因此人們對新型控制方法[67]進行了探索和研究，例如魯棒控制、自適應控制、預測控制、模糊控制、滑模控制等。

若隔振系統有模型不確定性，或者存在外部擾動，則閉環反饋控制系統可能出現不穩定。對此，研究人員基于魯棒理論設計了具有魯棒穩定性的控制器。

控制器的結構框圖如圖9所示。

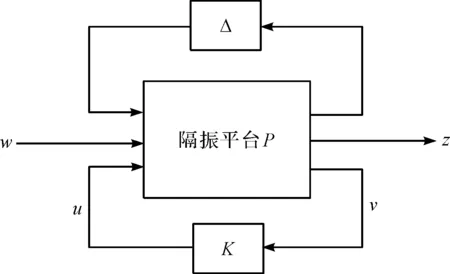
圖9 模型不確定性系統的魯棒控制Δ—模型不確定性；K—控制器；w—外界干擾；u—控制輸入；v—反饋信號；z—系統輸出

針對系統模型不確定性、多控制目標，OOMEN等[68]設計了基于H∞范數在線估計的魯棒控制器，對多維微振動干擾進行抑制。根據魯棒控制理論，利用H2控制可以保證系統的名義性能，利用H∞控制可以提高系統在參數不確定或高頻模態未建模時的魯棒穩定性。MELEIS等[69]設計了H2/H∞復合控制器，并通過實驗分析了其在微重力隔振系統上的有效性。為提高控制器的實時性，對H2/H∞控制器進行了降階處理。除了H2和H∞控制外，μ綜合控制也在微振動主動隔振系統中得到了應用。μ綜合控制的基本原理是對隔振系統的結構奇異值進行最優化，這樣即使隔振系統的剛度和阻尼在一定范圍內變化，隔振系統仍具有良好的魯棒穩定性和魯棒性能。

當隔振系統的模型參數或者周圍環境特征緩慢變化時，利用自適應算法調節控制器的參數，能實現微振動的有效控制。ZUO等[70]提出了自適應模型趨近控制方法，不同于傳統的模型參考自適應控制方法，它的控制目標是模型的狀態變量而不是跟蹤誤差，控制器中的參考模型是5.1節中提到的“天棚模型”。考慮到柔性梁在旋轉過程中彈性模量和轉動慣量會發生變化，LI等[71]設計了一種輸出力矩能自動調節的自適應控制器。魯棒自適應控制器結合了魯棒控制和自適應控制的優點，既能應對隔振系統的模型參數不確定性問題，又能解決系統中未知的非線性問題。SUN等[72,73]將魯棒自適應控制方法應用于電液驅動的主動懸置系統。

考慮到主動懸置系統在運行過程中有效負載的質量會發生變化，LI等[74]利用Takagi-Sugeno模糊方法建立了系統的模糊模型，當系統的載荷質量變化時，該模型的輸出也會隨之變化；在模糊模型的基礎上，作者設計了滑?？刂破?，使得系統的狀態變量在特定的滑模平面上變化。

6 研究展望

6.1 驅動傳感一體式隔振系統

在一些應用場合中，受到結構尺寸的限制以及使用環境的影響，驅動器不能較好地和外部傳感器兼容。基于自傳感技術的微振動隔振平臺是一種較為理想的解決方案。這種技術在反饋量易自檢的驅動器中比較常見，如靜電、壓電[75-77]和電力[78]驅動器。基于MEMS的驅動傳感一體化隔振系統具有體積小、功率密度高等優點，應用前景廣泛。

6.2 振動能量回收

微振動的主動控制是通過驅動器主動耗散微振動干擾產生的能量。從提高能量利用率的角度出發，可采用能量循環裝置對外界振動能量進行回收和利用，實現驅動器的能量供應[79,80]。隨著能量回收技術的發展，滿足綠色節能要求的隔振裝置會受到更多的關注。

6.3 控制方法的發展

微振動隔振系統是一種復雜的機械裝置，存在時變、非線性、耦合(包括多物理場、剛柔、多自由度耦合等)等綜合性動力學問題，采用傳統的控制方法很難解決這些問題。因此，基于模型在線辨識的自適應控制，基于智能算法/模型的神經網絡控制[81]、模糊推理控制[82]和多變量魯棒控制等技術將得到更充分的研究。

7 結束語

本文圍繞微振動及其隔離標準，主動微振動隔離平臺的構型、驅動、建模、控制等內容進行展開，對近年來微振動主動隔振系統的研究成果進行了綜述；介紹了微振動隔離的標準，指出基于絕對速度均方根的振動標準曲線是評判微振動隔離效果的標準之一；闡述了單軸主動隔振系統的基本原理和多軸主動隔振系統的應用場合，重點說明了基于Stewart構型的六自由度微振動隔離平臺；總結了常見的微振動隔振系統的驅動器，重點論述了智能材料(壓電和超磁致伸縮)驅動器在微振動隔振系統中的應用；歸納了微振動主動隔振系統的結構動力學建模方法、驅動器的遲滯建模方法；基于前饋、反饋、復合以及其他新型控制原理，對微振動隔振系統的主動控制方法進行了論述。

最后，本文圍繞驅動傳感一體化、振動能量回收、新型振動控制方法等內容，對微振動主動隔振系統的研究進行了展望。