模切刀架軸承的軸向預(yù)緊力優(yōu)化研究*
葉 超,徐旭松,*,劉艷旭,朱敏浩
(1.江蘇理工學(xué)院 機(jī)械工程學(xué)院,江蘇 常州 213001;2.江蘇麒浩精密機(jī)械股份有限公司,江蘇 寶應(yīng) 225800)
0 引 言
模切刀架屬于圓壓圓模切機(jī)中最為重要的部件,其工作質(zhì)量的好壞直接影響到最終模切成品的優(yōu)劣。用戶對(duì)模切機(jī)刀輥運(yùn)動(dòng)的穩(wěn)定性、可靠性和模切精度要求越來越高,因此在設(shè)計(jì)階段,就需對(duì)模切刀架進(jìn)行受力計(jì)算、強(qiáng)度和剛度的校核。
張慶山等[1]對(duì)模切刀輥進(jìn)行了靜、動(dòng)態(tài)分析,從減小模切刀輥的質(zhì)量入手,對(duì)軸進(jìn)行了結(jié)構(gòu)優(yōu)化設(shè)計(jì);張平格等[2]運(yùn)用Workbench軟件對(duì)模切刀輥送紙機(jī)構(gòu)中的曲柄滑塊部分進(jìn)行了優(yōu)化分析,為確保運(yùn)動(dòng)平穩(wěn)性提供準(zhǔn)確、可靠的技術(shù)參數(shù);廖昌城[3]從模切刀輥結(jié)構(gòu)入手討論了影響模切刀輥的使用壽命和保證其正常工作的因素,提出并設(shè)計(jì)了刃尖與砧輥表面保持“零間隙”的措施和合理結(jié)構(gòu);郭鐵能[4]等通過建立軸承內(nèi)圈離心膨脹力和溫升的熱位移模型,并利用Timoshenko理論建立了主軸模型,研究了軸承過盈狀態(tài)下的動(dòng)力學(xué)特性;于清煥等[5]針對(duì)復(fù)雜的空間環(huán)境,建立了軸承靜力學(xué)預(yù)緊模型,分析了多因素下軸承預(yù)緊力的變化規(guī)律[6]。
以上研究均是對(duì)所建模型進(jìn)行的結(jié)構(gòu)假設(shè)和基于理論的結(jié)構(gòu)優(yōu)化,對(duì)于研究結(jié)果并沒有一個(gè)合理的驗(yàn)證,且未考慮實(shí)際裝配中的軸向預(yù)緊力對(duì)模型的影響。
本文以圓壓圓模切刀架的上刀輥為研究對(duì)象,將軸承預(yù)緊力代入剛度計(jì)算式中,以軸承的軸向剛度和作用在套圈上的力作為設(shè)計(jì)變量,利用Workbench響應(yīng)曲面優(yōu)化方法找出最佳預(yù)緊剛度,為尋找最佳的軸承預(yù)緊力提供依據(jù)。
1 過盈狀態(tài)下軸承徑向、軸向剛度計(jì)算
圓壓圓模切機(jī)有上、下兩輥,即切割用的上刀輥和壓配用的下砧輥,上刀輥和下砧輥軸承位零件完全相同。
弧切上刀輥模型結(jié)構(gòu)如圖1所示。
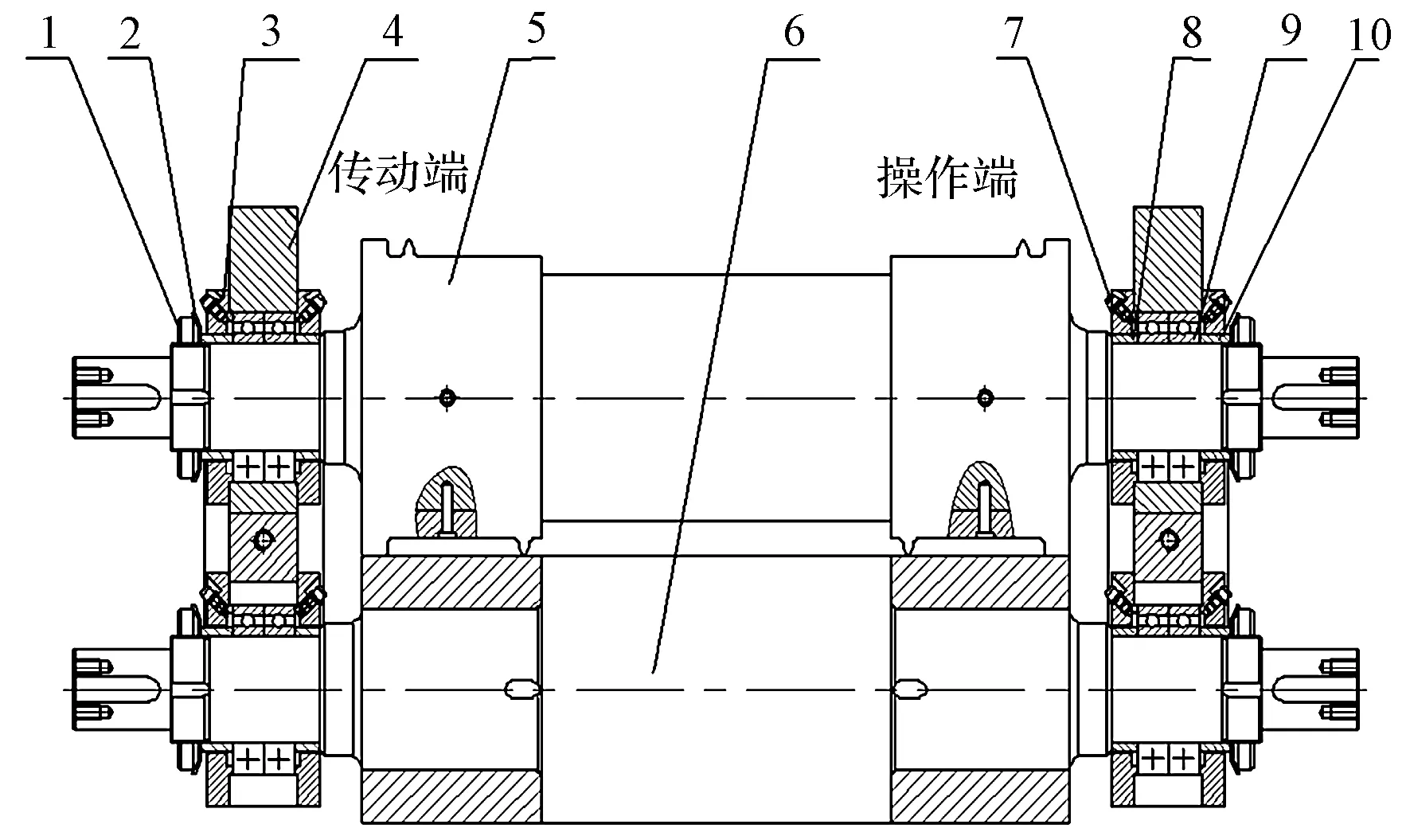
圖1 弧切上刀輥模型結(jié)構(gòu)1—圓螺母;2—止動(dòng)墊圈;3—軸承端蓋;4—軸承座;5—硬質(zhì)合金刀具;6—下砧輥;7—油杯;8—內(nèi)套筒;9—6012軸承;10—外套筒

因只研究軸承過盈狀態(tài)下的上刀輥的靜、動(dòng)態(tài)特性,此處取內(nèi)圈和軸頸的配合過盈量的范圍-0.013 mm~0 mm,外圈和軸承座的配合過盈量范圍-0.018 mm~0 mm。已知配合過盈量范圍,可計(jì)算出內(nèi)圈溝道徑向位移和外圈溝道徑向位移之和(δe+δi)的范圍[7]為0~0.028 mm,其對(duì)應(yīng)的最小過盈狀態(tài)和最大過盈狀態(tài)的初始接觸角分別為10.11°和17.77°。
軸承技術(shù)參數(shù)如表1所示。
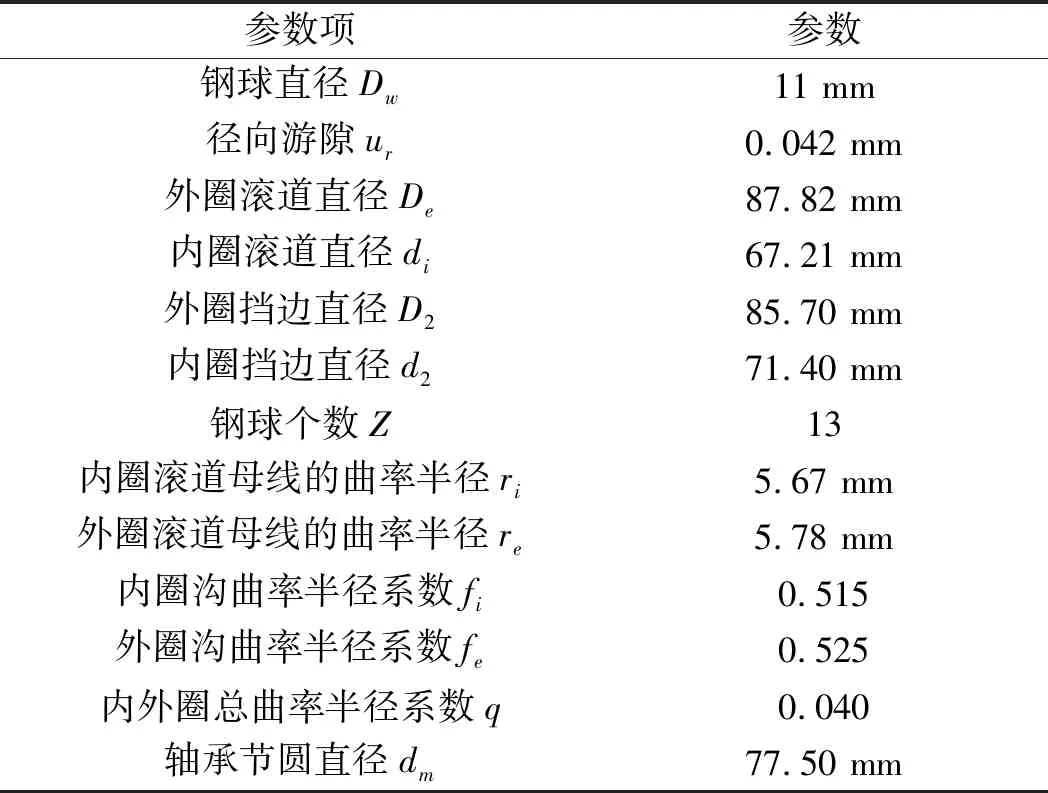
表1 軸承技術(shù)參數(shù)
對(duì)于徑向游隙大于零的深溝球軸承,在徑向位移和徑向變形的影響下,滾動(dòng)體的載荷分布位置與軸承的徑向平面成一定角度,此時(shí)作用在鋼球上的載荷使得鋼球與滾道接觸點(diǎn)處公法線和徑向平面也呈一定角度;由于不考慮軸承發(fā)熱和離心力對(duì)計(jì)算結(jié)果的影響,可認(rèn)為負(fù)荷極限角與過盈狀態(tài)下的接觸角相等[8],因而有:
(1)
(2)
式中:α—初始過盈狀態(tài)下的接觸角;ψ1—負(fù)荷極限角;ε—非常小的數(shù);Kn—鋼球與套圈之間總負(fù)荷變形常數(shù),其值與配合過盈量下的接觸角有關(guān);Jr(ε)—負(fù)荷分布徑向積分;n—接觸系數(shù),球軸承取n=1.5;δmax—配合過盈量下鋼球的最大接觸變形,mm;Fr—徑向載荷,N;μr—軸承游隙,mm;Z—滾動(dòng)體數(shù)。
此時(shí)軸向預(yù)緊接觸角α1與徑向預(yù)緊下的初始過盈狀態(tài)下的接觸角α的關(guān)系為:
(3)
式中:Fa—作用在軸承蓋上螺栓的預(yù)緊力,N;Z—滾動(dòng)體數(shù);Dw—滾動(dòng)體直徑,mm;q—總曲率半徑系數(shù)。
將已知接觸角和徑向、軸向力代入公式可得軸承徑向和軸向剛度分別為:
(4)
(5)
式中:α—初始過盈狀態(tài)下的接觸角;α1—實(shí)際軸向預(yù)緊力下的接觸角;Z—滾動(dòng)體數(shù);Kr—徑向剛度,N/mm;Ka—軸向剛度,N/mm;Dw—滾動(dòng)體直徑,mm;Fa—作用在軸承蓋上螺栓的預(yù)緊力,N。
將最小和最大過盈狀態(tài)下算得的徑向力Fr代入式(4),將實(shí)際軸向預(yù)緊力Fa=8 500 N代入式(5),則有:
(1)在最小過盈狀態(tài)下:
Kr=18 101.77 N/mm,Ka=174 123.47 N/mm;
(2)在最大過盈狀態(tài)下:
Kr=30 498.95 N/mm,Ka=219 022.20 N/mm。
2 軸向預(yù)緊力的校核
過盈量的不同會(huì)導(dǎo)致接觸狀態(tài)的不同,過盈狀態(tài)下的極限接觸角計(jì)算公式為[9]:
(6)
式中:na—與接觸點(diǎn)主曲率差函數(shù)F(ρ)有關(guān)的系數(shù);α—初始過盈狀態(tài)下的接觸角;∑ρ—主曲率和函數(shù);α2—受載后的極限接觸角;θ—擋邊邊緣球心連線與徑向平面的夾角。
取內(nèi)、外圈算出數(shù)值的較小值作為極限接觸角[10],代入下式可計(jì)算出極限軸向載荷:
(7)
式中:Fa max—極限軸向載荷,N。
根據(jù)軸承的已知參數(shù),查得θe=36.17°,θi=51.75°,最小過盈狀態(tài)下的α=10.11°,nae=3.03,nai=4.15;最大過盈狀態(tài)下的α=17.77°,nae=3.03,nai=4.12。算得在最小過盈狀態(tài)下,α2=21.15°,軸向極限負(fù)荷Fa max=6 247.79 N;在最大過盈狀態(tài)下,α2=23.61°,軸向極限負(fù)荷Fa max=4 113.18 N。
軸承端蓋預(yù)緊情況如圖2所示。

圖2 軸承端蓋預(yù)緊
車間實(shí)際裝配時(shí),對(duì)軸承端蓋施加的軸向預(yù)緊力為8 500 N,明顯大于計(jì)算出的極限軸向預(yù)緊力。過大的軸向預(yù)緊力會(huì)對(duì)軸承的接觸狀態(tài)產(chǎn)生影響,不僅會(huì)降低軸承的壽命,還會(huì)降低整個(gè)結(jié)構(gòu)的運(yùn)動(dòng)精度;另外,實(shí)際軸向預(yù)緊力大于極限軸向預(yù)緊力會(huì)增加機(jī)構(gòu)的不穩(wěn)定性,上刀輥極有可能會(huì)發(fā)生共振,刀口位置很容易發(fā)生崩裂,從而對(duì)生產(chǎn)切割產(chǎn)生影響。因此,有必要對(duì)軸向預(yù)緊力進(jìn)行優(yōu)化。
3 有限元建模
3.1 模型簡(jiǎn)化
為了便于有限元模型的計(jì)算和分析,需要對(duì)圖1的上刀輥模型進(jìn)行簡(jiǎn)化[11]:
(1)硬質(zhì)合金刀具和輥軸通過螺釘固定,可將刀具與輥軸視為同等密度材料,將刀具作為輥軸的附加分布質(zhì)量集中等效到輥軸單元模型上;
(2)將深溝球軸承視為彈性支撐,分別在徑向軸承接觸線和軸向軸承位端面與端面接觸線處用彈簧單元代替軸承,將其角剛度忽略,僅考慮軸向剛度和徑向剛度。
3.2 模型建立與有限元分析
上刀輥結(jié)構(gòu)模型如圖3所示。

圖3 上刀輥結(jié)構(gòu)模型
根據(jù)上述簡(jiǎn)化原則,筆者利用3D軟件Solidworks對(duì)上刀輥結(jié)構(gòu)進(jìn)行了有限元建模。為方便分析軟件的計(jì)算,需對(duì)結(jié)構(gòu)的倒角、微小圓孔等特征進(jìn)行處理,再導(dǎo)入ANSYS Workbench中。
上刀輥網(wǎng)格劃分模型如圖4所示。

圖4 上刀輥的網(wǎng)格劃分模型
此處,筆者采用Mesh工具對(duì)上刀輥結(jié)構(gòu)進(jìn)行網(wǎng)格劃分,兩處圓螺母螺紋處采用四面體網(wǎng)格,網(wǎng)格單元設(shè)置為6 mm,對(duì)整體使用自動(dòng)網(wǎng)格劃分,除圓螺母螺紋處外,其他網(wǎng)格單元設(shè)置為8 mm。
上刀輥材料參數(shù)如表2所示。

表2 上刀輥材料參數(shù)
上刀輥所受到的約束:軸承對(duì)刀輥軸的約束;上刀輥繞Z軸以500 r/min的旋轉(zhuǎn)速度轉(zhuǎn)動(dòng)。
軸承模擬示意圖如圖5所示。
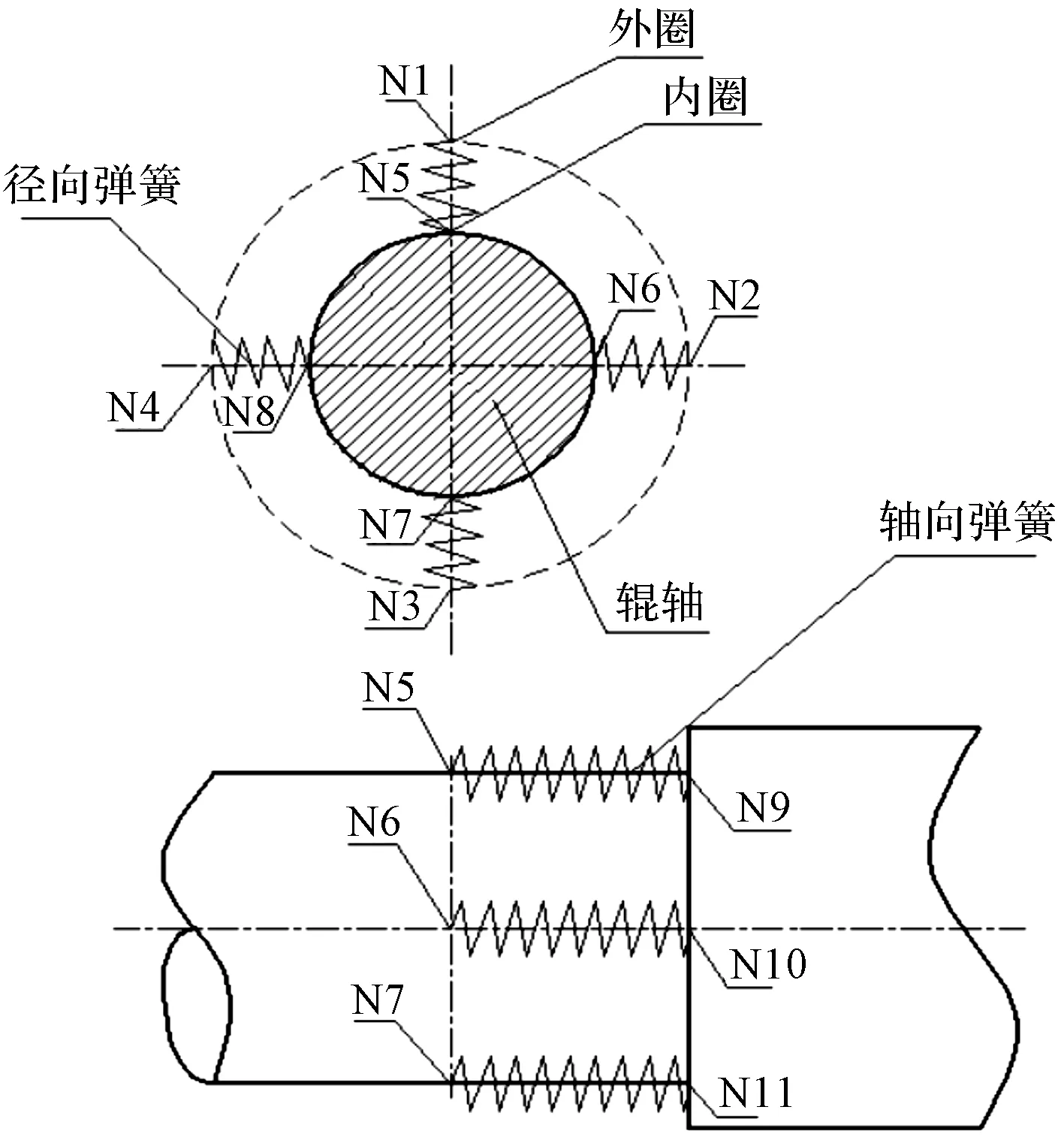
圖5 軸承模擬示意圖
軸承在高速運(yùn)轉(zhuǎn)時(shí),根據(jù)簡(jiǎn)化規(guī)則考慮軸承只具有徑向和軸向剛度,因此,在軸承位的軸向和徑向分別用4個(gè)壓縮彈簧單元來模擬軸承。N1~N12為模擬軸承時(shí)定義在徑向接觸線處與軸向端面,以及軸向端面與端面接觸線處的遠(yuǎn)程點(diǎn)。對(duì)于預(yù)應(yīng)力的模態(tài)分析來說,阻尼對(duì)結(jié)構(gòu)固有頻率的影響很小,故不考慮阻尼的影響,設(shè)置阻尼為零。
彈簧作為體對(duì)地連接,參考點(diǎn)作為固定點(diǎn),移動(dòng)點(diǎn)設(shè)為定義在輥軸軸承位處的遠(yuǎn)程點(diǎn),固定端徑向彈簧N1、N2、N3、N4完全固結(jié),N5、N6、N7、N8僅釋放其軸向轉(zhuǎn)動(dòng)自由度;游動(dòng)端N1、N2、N3、N4完全固結(jié),N5、N6、N7、N8僅限制其X、Y方向的轉(zhuǎn)動(dòng)自由度。對(duì)于軸向彈簧,其移動(dòng)點(diǎn)對(duì)應(yīng)于徑向彈簧內(nèi)圈上的點(diǎn),點(diǎn)與點(diǎn)之間剛性耦合,使得它們之間連接的面或線相互作用[12];一端配置2個(gè)軸承,模擬后通過4個(gè)彈簧均布在軸承位周圍,整體剛度也需均布在彈簧上。
在最小過盈狀態(tài)下,每個(gè)徑向彈簧剛度為9 050.90 N/mm,每個(gè)軸向彈簧剛度為87 061.70 N/mm,同時(shí)作用在每個(gè)軸向彈簧上的力為1 500 N。
最小過盈狀態(tài)下的仿真結(jié)果如圖6所示。

圖6 最小過盈狀態(tài)下的仿真結(jié)果
由圖6的仿真結(jié)果可知:最大變形出現(xiàn)在軸承固定端,最大應(yīng)力處于軸承約束處;一階振型的固有頻率為205.16 Hz,根據(jù)臨界轉(zhuǎn)速與頻率的關(guān)系可知n=60f(n—轉(zhuǎn)速,r/min;f—頻率,Hz),則上刀輥的一階臨界轉(zhuǎn)速為12 309.60 r/min,遠(yuǎn)大于上刀輥的工作轉(zhuǎn)速500 r/min,因此,在最小過盈狀態(tài)下上刀輥不會(huì)發(fā)生共振;
在最大過盈狀態(tài)下,每個(gè)徑向彈簧剛度為15 249.50 N/mm,每個(gè)軸向彈簧剛度為109 511.10 N/mm,作用在軸向彈簧上1 500 N力。
最大過盈狀態(tài)下的仿真結(jié)果如圖7所示。

圖7 最大過盈狀態(tài)下的仿真結(jié)果
由圖7的仿真結(jié)果可知:最大變形依然出現(xiàn)在軸承固定端,最大應(yīng)力出現(xiàn)在軸承約束處;一階振型的固有頻率為234.88 Hz,則一階臨界轉(zhuǎn)速為14 092.80 r/min,遠(yuǎn)大于上刀輥的工作轉(zhuǎn)速500 r/min。因此,在最大過盈狀態(tài)下,上刀輥也不會(huì)發(fā)生共振;
在最小和最大過盈狀態(tài)下,實(shí)際軸向預(yù)緊力滿足結(jié)構(gòu)的振動(dòng)條件,卻不滿足極限軸向預(yù)緊力的條件;過大的軸向預(yù)緊力會(huì)對(duì)軸承的接觸狀態(tài)產(chǎn)生影響,不僅會(huì)降低軸承的壽命,還會(huì)降低整個(gè)結(jié)構(gòu)的運(yùn)動(dòng)精度[13],因此,還需要對(duì)軸向預(yù)緊力進(jìn)行優(yōu)化。
4 軸向預(yù)緊力優(yōu)化
4.1 優(yōu)化變量選擇
最小過盈狀態(tài)優(yōu)化前初值及取值范圍如表3所示。

表3 最小過盈狀態(tài)優(yōu)化前初值及取值范圍
最大過盈狀態(tài)優(yōu)化前初值及取值范圍如表4所示。

表4 最大過盈狀態(tài)優(yōu)化前初值及取值范圍
在最小和最大過盈狀態(tài)下的仿真結(jié)果中,最大變形和最大應(yīng)力均發(fā)生在軸承約束處,因此以最大變形和最大應(yīng)力作為輸出參數(shù);在上刀輥的材料及結(jié)構(gòu)尺寸不變的情況下,使用軸向剛度和施加在軸向彈簧上的力為輸入?yún)?shù),對(duì)上刀輥進(jìn)行響應(yīng)曲面優(yōu)化設(shè)計(jì),優(yōu)化的目標(biāo)是尋找最佳預(yù)緊力,使得最大變形和最大應(yīng)力最小,同時(shí)使得一階臨界轉(zhuǎn)速遠(yuǎn)大于工作轉(zhuǎn)速。
4.2 優(yōu)化結(jié)果
基于響應(yīng)曲面優(yōu)化的方法,筆者對(duì)上刀輥軸向剛度進(jìn)行優(yōu)化,優(yōu)化后各項(xiàng)數(shù)值發(fā)生了相應(yīng)的變化。
最小過盈狀態(tài)優(yōu)化前后參數(shù)值對(duì)比如表5所示。
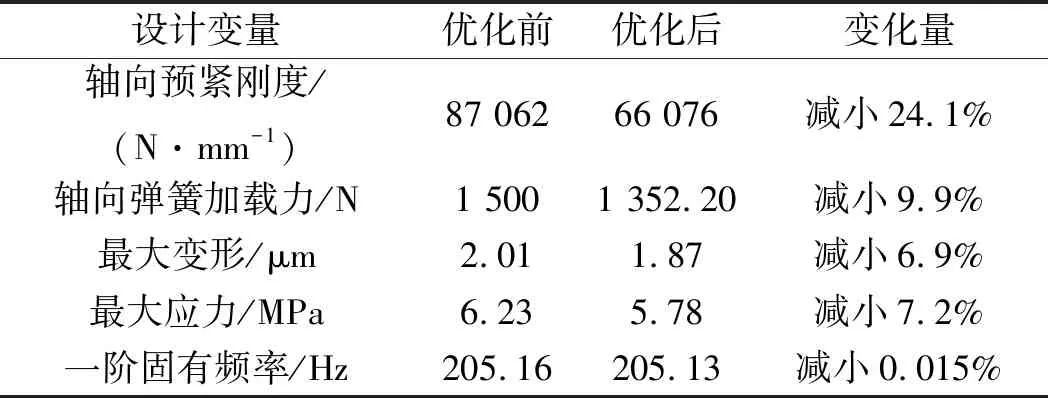
表5 最小過盈狀態(tài)優(yōu)化前后參數(shù)值對(duì)比
由表5可以看出:最小過盈狀態(tài)下優(yōu)化后的軸向預(yù)緊剛度已小于最小過盈狀態(tài)下的軸向極限剛度,相對(duì)于優(yōu)化前減小了24.1%,最大變形減小6.9%,最大應(yīng)力減小7.2%,一階固有頻率比優(yōu)化前減小0.015%,在給定的工作轉(zhuǎn)速下,上刀輥并不會(huì)產(chǎn)生共振。
最大過盈狀態(tài)優(yōu)化前后參數(shù)值對(duì)比如表6所示。

表6 最大過盈狀態(tài)優(yōu)化前后參數(shù)值對(duì)比
由表6可以看出:最大過盈狀態(tài)下優(yōu)化后的軸向預(yù)緊剛度已小于最大過盈狀態(tài)下的軸向極限剛度,相對(duì)于優(yōu)化前減小35.2%,最大變形減小5.1%,最大應(yīng)力減小5.1%,一階固有頻率比優(yōu)化前減小0.008 5%,在給定的工作轉(zhuǎn)速下,上刀輥并不會(huì)產(chǎn)生共振;
相比于優(yōu)化前不合理的軸向預(yù)緊剛度,優(yōu)化后的軸向預(yù)緊剛度均處于安全范圍內(nèi),對(duì)于上刀輥的影響大大減小。
優(yōu)化后的剛度范圍為66 076 N/mm~70 960 N/mm,預(yù)緊剛度與預(yù)緊力的關(guān)系[14]如下式:
(8)
式中:α—初始配合過盈量下的接觸角;α3—優(yōu)化后的接觸角。
將優(yōu)化后剛度范圍值代入式(8)中,可計(jì)算出接觸角α3的值,然后代入任一式中可得軸向端蓋預(yù)緊力的范圍為3 823.09 N~6 143.25 N;
同時(shí),優(yōu)化后軸向彈簧加載力(即套圈力)為5 408.80 N,則最佳的軸承預(yù)緊力范圍為9 231.89 N~11 552.05 N。
5 可靠性分析
六西格瑪技術(shù)主要是運(yùn)用概率分析的方法來評(píng)估產(chǎn)品設(shè)計(jì)的可靠性。此處筆者利用ANSYS Workbench中的Six sigma analysis模塊來評(píng)估優(yōu)化后軸向預(yù)緊力的可靠性。在最小過盈狀態(tài)下的理論剛度最小,最大等效應(yīng)力是最大的,要保證在最小和最大過盈狀態(tài)之間實(shí)際裝配的軸向剛度所造成的應(yīng)力值小于這個(gè)數(shù),那么取最小過盈狀態(tài)優(yōu)化前的最大等效應(yīng)力為可靠性指標(biāo)。
最小過盈狀態(tài)下最大等效應(yīng)力的累積分布函數(shù)如圖8所示。
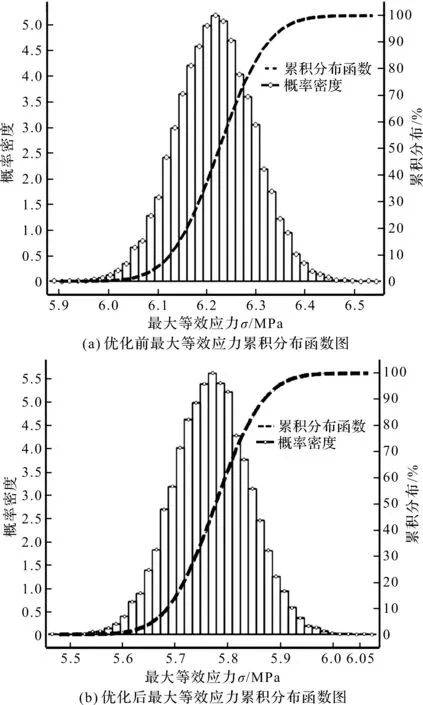
圖8 最小過盈狀態(tài)下最大等效應(yīng)力累積分布函數(shù)圖
圖8是在最小過盈狀態(tài)下優(yōu)化前后分別進(jìn)行10 000次隨機(jī)抽樣后所得分布柱狀圖,其輸出的結(jié)果最大等效應(yīng)力的柱狀圖并沒有較大的間隙和跳躍,柱狀圖分布良好,因此,其模擬次數(shù)已足夠。
最小過盈狀態(tài)優(yōu)化前最大等效應(yīng)力參數(shù)概率表如表7所示。
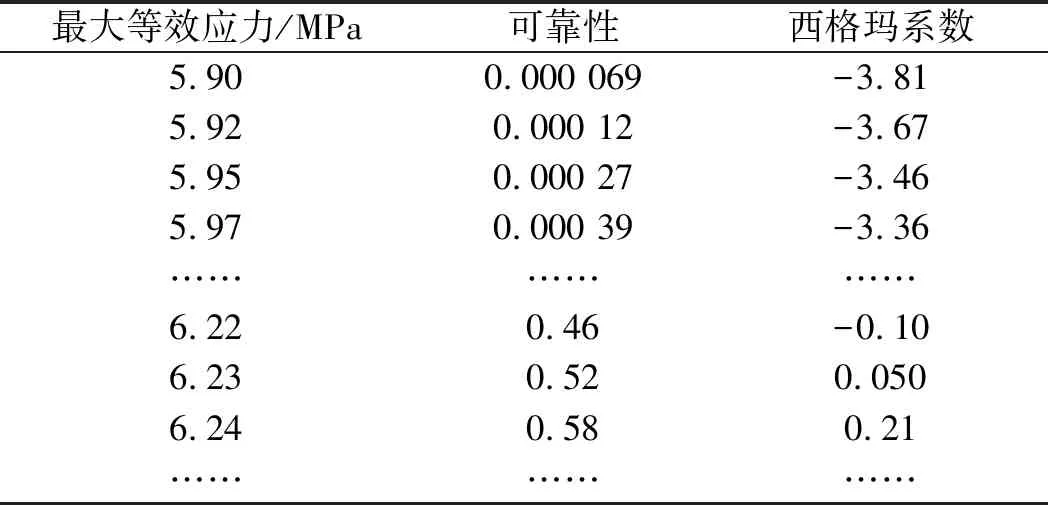
表7 最小過盈狀態(tài)優(yōu)化前最大等效應(yīng)力參數(shù)概率表
由表7可知,優(yōu)化前最大等效應(yīng)力為6.23的可靠度為52%。
最小過盈狀態(tài)優(yōu)化后最大等效應(yīng)力參數(shù)概率表如表8所示。

表8 最小過盈狀態(tài)優(yōu)化后最大等效應(yīng)力參數(shù)概率表
由表8可知,優(yōu)化后最大等效應(yīng)力6.23的可靠度達(dá)99%,因此在最小過盈狀態(tài)下優(yōu)化可行。
最大過盈狀態(tài)下最大等效應(yīng)力的累積分布函數(shù)如圖9所示。
圖9是在最大過盈狀態(tài)下優(yōu)化前后分別進(jìn)行10 000次隨機(jī)抽樣后所得分布柱狀圖,其輸出的結(jié)果最大等效應(yīng)力的柱狀圖并沒有較大的間隙和跳躍,柱狀圖分布良好,因此,其模擬次數(shù)已足夠。
最大過盈狀態(tài)優(yōu)化前最大等效應(yīng)力參數(shù)概率表如表9所示。


圖9 最大過盈狀態(tài)下最大等效應(yīng) 力累積分布函數(shù)圖

表9 最大過盈狀態(tài)優(yōu)化前最大等效應(yīng)力參數(shù)概率表
由表9可知,優(yōu)化前最大等效應(yīng)力為6.23的可靠度為98%。
最大過盈狀態(tài)優(yōu)化后最大等效應(yīng)力參數(shù)概率表如表10所示。

表10 最大過盈狀態(tài)優(yōu)化后最大等效應(yīng)力參數(shù)概率表
由表10可知,優(yōu)化后最大等效應(yīng)力6.23的可靠度達(dá)99%。由此可見,在最大過盈狀態(tài)下所作的優(yōu)化也是可行。
6 結(jié)束語
本文對(duì)模切刀架上刀輥的軸承在配合過盈狀態(tài)下的極限軸向預(yù)緊力進(jìn)行了理論計(jì)算,判斷出實(shí)際裝配預(yù)緊力大于軸承的軸向預(yù)緊力極限;采用ANSYS Workbench仿真軟件,對(duì)上刀輥軸承的軸向預(yù)緊力進(jìn)行了優(yōu)化和可靠性驗(yàn)證。
根據(jù)驗(yàn)證結(jié)果可知:在滿足極限軸向載荷的條件下,刀輥在最小和最大過盈狀態(tài)下的軸向剛度分別減小了24.1%和35.2%,最大等效應(yīng)力分別減小了7.2%和5.1%,最大變形分別減小了6.9%和5.1%;在實(shí)際裝配時(shí),軸向預(yù)緊力保持在9 231.89 N~11 552.05 N之間,模切刀架裝配返工的拆卸次數(shù)顯著減少。

