基于遺傳-粒子群混合優(yōu)化算法的拆卸序列規(guī)劃方法研究*

王玉鑫，任 帥

(中國民航大學 航空工程學院，天津 300300)

0 引 言

為確保使產(chǎn)品具有良好的維修性，并且保證新產(chǎn)品在投入運營后，可以正確地使用和維修，制造商應開發(fā)并提供正確、合理、詳盡、便于使用的新產(chǎn)品運行文件，后勤保障分析國際程序規(guī)范(S3000L)明確要求產(chǎn)品在設計階段應該考慮在運營階段和報廢階段的拆解，這要求在技術(shù)出版物中必須有相關(guān)拆解流程，即需要進行拆卸序列規(guī)劃(disassembly sequence planning，DSP)。

進行拆卸序列規(guī)劃在設計階段有助于提高產(chǎn)品的維修性，且可對技術(shù)出版物進行有效驗證；在運營階段或報廢階段也可以有效地在工程中提高工作效率，降低維修成本。

拆卸序列規(guī)劃的目的是生成零件或者部件的拆卸順序，以使得在維修工作中達到?jīng)Q策者的“最佳目標”，此最佳目標一般指拆卸成本最小、拆卸收益最大、對環(huán)境污染最小等要求，其好壞程度對于產(chǎn)品維修活動的有效性和經(jīng)濟性有著直接的影響[1]。

DSP問題本質(zhì)上可以抽象為一個排列組合的優(yōu)化問題，隨著產(chǎn)品零件數(shù)量的增加，拆卸序列的數(shù)量會呈指數(shù)型增長，即組合爆炸現(xiàn)象[2]。因此，DSP問題的求解將會是DSP問題的關(guān)鍵。對此，國內(nèi)外大量學者對其進行了深入研究，比如蟻群算法[3-5]、人工蜂群算法[6，7]、遺傳蝙蝠算法[8]等。

蟻群算法經(jīng)改進后具有良好的收斂性；人工蜂群算法起步較晚，在該問題的應用也較少，其同樣可在保證種群多樣性的前提下實現(xiàn)算法的快速收斂；雖鮮有人將蝙蝠算法用于拆卸序列規(guī)劃問題，但經(jīng)改進的遺傳蝙蝠算法的收斂性和收斂速度也優(yōu)于遺傳算法(GA)。TSENG Y J[9]等提出了一種基于粒子群算法(PSO)的閉環(huán)裝配與拆卸序列規(guī)劃的綠色裝配序列規(guī)劃模型，但是未考慮在通過粒子群迭代后的序列優(yōu)先關(guān)系；同樣地，張秀芬[10]在通過粒子群算法對拆卸序列進行尋優(yōu)中也未考慮新一代的序列是否滿足拆卸優(yōu)先約束；在后續(xù)研究中，張濟濤等[11]提出了基于量子遺傳算法的拆卸序列規(guī)劃模型，對該問題進行改進，其結(jié)論為迭代次數(shù)減少，可較快得出最優(yōu)解；然而其方法在每次迭代之后對所得出序列進行檢驗，若序列滿足優(yōu)先約束，則進入下一步，否則重新進行迭代。本質(zhì)上看，迭代次數(shù)要遠高于其所得次數(shù)，其迭代次數(shù)的減少并不可靠。因此，以上研究雖然可以有效地得出較優(yōu)的拆解序列，但是在其算法的迭代過程中或是未考慮優(yōu)先約束，或是迭代速度過慢。

基于此，為提高拆卸序列規(guī)劃的效率，在工程中更快、更精準地得出最優(yōu)解，本文根據(jù)產(chǎn)品零件的裝配約束關(guān)系，通過拆解優(yōu)先圖來表達拆解對象，并提出一種基于遺傳-粒子群混合優(yōu)化算法(GA-PSO)；最后以液壓泵作為算例，來驗證算法的可行性及優(yōu)越性。

1 產(chǎn)品拆卸優(yōu)先圖建模

1.1 拆卸優(yōu)先圖建立

本文所涉及的拆卸序列規(guī)劃主要是完全拆卸，其目標函數(shù)一般為時間最短，所以選用較簡單的拆卸優(yōu)先圖進行表達，若為選擇性拆卸則不適用。

拆卸優(yōu)先圖可以簡單有效地表達產(chǎn)品的拆卸優(yōu)先約束關(guān)系[12]，拆卸優(yōu)先圖如圖1所示。

圖1 拆卸優(yōu)先圖

圖1中，A、B、C、D、E、F分別表示該產(chǎn)品的組成構(gòu)件，有向箭頭代表約束關(guān)系，表示各部件優(yōu)先約束關(guān)系，如F→A表示在拆卸A之前，必須先拆卸F。

不同于之前研究的表達，本文所采用的拆解優(yōu)先圖使用分層表達，A為第0層，B、C為第一層，D為第二層，E為第三層，F(xiàn)為第四層。分層表達便于對序列進行“合規(guī)化處理”，“合規(guī)化處理”即為對隨機序列進行處理使其滿足優(yōu)先約束。

1.2 模型的數(shù)學描述

DSP為離散組合優(yōu)化問題，基于拆卸優(yōu)先圖模型，可將此問題描述為：

產(chǎn)品可拆卸單元為N個，每次僅能拆卸其中一個，所求序列應該滿足拆卸優(yōu)先關(guān)系，并且每個頂點都需遍歷且只能遍歷一次。

A-F按1-6進行排列，拆卸優(yōu)先矩陣R如下式所示：

(1)

其中，Rrc—矩陣R的第r行第c列位置的數(shù)值，

Rrc=

4即為拆卸優(yōu)先矩陣層數(shù)。

通過搜索優(yōu)先矩陣可以將隨機序列進行合規(guī)化處理，合規(guī)化處理流程圖如圖2所示。

圖2 合規(guī)化處理流程圖

M—拆卸優(yōu)先矩陣層數(shù)

對于完全拆卸序列規(guī)劃，其總拆卸操作時間一致，由于總時間=總拆卸操作時間+操作換向時間+變換工具時間，則可以將目標函數(shù)看作換向次數(shù)及工具變換次數(shù)的函數(shù)。該目標函數(shù)即可作為算法中的適應度函數(shù)。

(1)拆卸工具變換次數(shù)如下式所示：

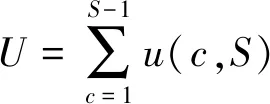
(2)

(2)拆卸方向變換次數(shù)如下式所示：

(3)

2 GA-PSO混合優(yōu)化算法

2.1 算法原理及模型映射

2.1.1 算法1 (粒子群算法)

粒子群算法采用群體進化，通過適應度函數(shù)評價每個粒子的好壞，模擬鳥群飛行覓食行為，集體協(xié)作尋找最優(yōu)解。將鳥群作為一個粒子群，每只鳥作為G維空間的一個粒子，其代表問題的一個可行解，具有位置和速度兩個屬性。

粒子位置坐標即為解向量，可通過適應度函數(shù)對其進行評價，各粒子可以通過自身所經(jīng)歷的位置、最佳位置和全局最佳位置提供的信息，在解空間內(nèi)不斷更新，尋找最優(yōu)解[13]。個體最優(yōu)解為粒子本身所經(jīng)歷的最佳位置，全局最優(yōu)解為種群所經(jīng)歷的最佳位置。

傳統(tǒng)的連續(xù)性尋優(yōu)規(guī)則一般如下：

G維空間粒子i的信息可表示為：

位置信息如下：

xi=(xi1,xi2,…,xiG)

(4)

速度信息如下：

vi=(vi1,vi2,…,viG)

(5)

根據(jù)個體最優(yōu)解和全局最優(yōu)解進化，速度更新如下：

(6)

位置更新如：

(7)

2.1.2 算法2 (遺傳算法)

解決拆卸序列規(guī)劃問題可直接采用零件或者操作編號進行編碼，通過選擇算子對各染色體進行選擇以得到父代染色體，再通過交叉、變異算子[14-16]。對種群染色體進行迭代尋找最優(yōu)解。

傳統(tǒng)的遺傳算法中，選擇算子一般選用輪盤賭選擇法。具體方法為將每個粒子被選擇的概率設定為該粒子的適應度所占種群總適應度的大小，若適應度越小越好，則通過各個粒子適應度與種群總適應度的差值之間的比值來確定。例如：3個粒子適應度為1、4、5，則總適應度為10，3個粒子被選擇概率的比值為9 ∶6 ∶5，三者被選擇的概率分別為0.45、0.3、0.25。

交叉算子一般是隨機確定一個或幾個交叉點的位置，然后將兩個染色體的基因進行交換，從而選擇兩個新的個體。

變異算子一般是隨機選擇某染色體的某個位置，在其可變范圍內(nèi)進行按一定規(guī)則隨機變化。

2.2 遺傳-粒子群混合優(yōu)化算法

粒子群算法多適用于連續(xù)組合優(yōu)化問題[17]，通過PSO求解DSP這種離散問題，需通過以下方法將其進行對應。

在產(chǎn)品模型基礎上，產(chǎn)生多個粒子，每個粒子由1-N的自然數(shù)組成，即可構(gòu)成一個粒子群：

(1)粒子的位置：對應拆卸序列；

(2)粒子的速度：前人將速度取值空間定為0,1來代表至下一代粒子元素是否發(fā)生變動。但是，通過此方式進行粒子的移動會產(chǎn)生不合規(guī)的粒子，需要再對粒子進行合規(guī)劃處理。因此，本文取消粒子群中的速度概念；

(3)粒子的適應度：對應拆卸成本函數(shù)，其值越小，序列越佳。

遺傳算法在求解DSP問題時同樣需要進行改進，傳統(tǒng)的交叉、變異算子可能導致從原本合規(guī)的父代染色體得到不合規(guī)的子代染色體。因此，要重新設計交叉及變異算子：

(1)交叉是GA更新和探索解空間的關(guān)鍵操作。傳統(tǒng)的交叉算子可能會導致序列錯誤，比如FEDBAC與FECDBA在第3個點交叉則產(chǎn)生FECBAC與FEDDBA。

為保證基因的完整性，將使用優(yōu)先選擇交叉方式進行交叉[18]，優(yōu)先保存交叉算子如圖3所示。

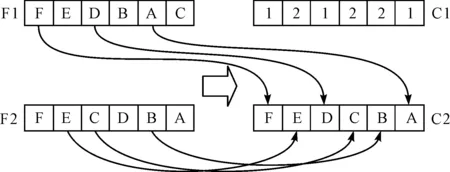
圖3 優(yōu)先保存交叉算子F1—父代1；F2—父代2；C1—子代掩碼，C2—子代

步驟如下：①隨機生成序列C1，該序列為1-2的隨機排列，長度與染色體長度相同；②C1中第一個數(shù)字是1，則C2第一個基因從F1的第一個基因提取，并刪除F1與F2中的該基因；③第二個數(shù)字是2，則C2從父代2的第一個染色體提取，并刪除F1與F2的該基因；④重復以上步驟即可得出新染色體C2；

(2)變異算子。不同于傳統(tǒng)變異算子，變異算子不能簡單地選取任意兩點進行置換，原因是交換后的染色體可能不能滿足優(yōu)先約束，合規(guī)化處理后可能與變異前相同，變異無效。對其進行改進，任取兩點將兩點間所有基因倒序排列，再經(jīng)過合規(guī)化處理后變異有效的概率較高。

由于粒子群算法種群中一旦產(chǎn)生相對較優(yōu)的粒子，則粒子都會朝著該粒子進化，若該粒子并非全局最優(yōu)，且全局最優(yōu)的方向與此粒子的方向相反，則粒子將無法找到全局最優(yōu)解，使得其局部搜索能力較強。在對求解質(zhì)量要求不高時，該算法可高效求得高質(zhì)量的解，但并非最優(yōu)解。因此，隨著PSO算法的不斷更新迭代，種群多樣性必然減少，易陷入局部最優(yōu)，從而得到局部最優(yōu)解。

另外，拆卸序列規(guī)劃問題是離散型數(shù)值尋優(yōu)問題，且其序列順序已被約束，這容易導致初始種群本身很可能已散落在局部最優(yōu)解附近，以致無法尋找到全局最優(yōu)解，從而得不出最優(yōu)序列。遺傳算法通過變異可提高其全局搜索性，將遺傳算法與粒子群算法進行結(jié)合，可以增強粒子群算法的全局搜索能力。

稱之為覆蓋粒規(guī)則(xi)B→Dk的置信度,其中|·|指一個集合的基數(shù)。如果conf((xi)B→Dk)=1,則(xi)B→Dk稱為一條確定性規(guī)則;否則稱之為一條可能性規(guī)則。

因此，本研究提出了GA-PSO混合的優(yōu)化算法。

遺傳-粒子群混合優(yōu)化算法流程圖如圖4所示。

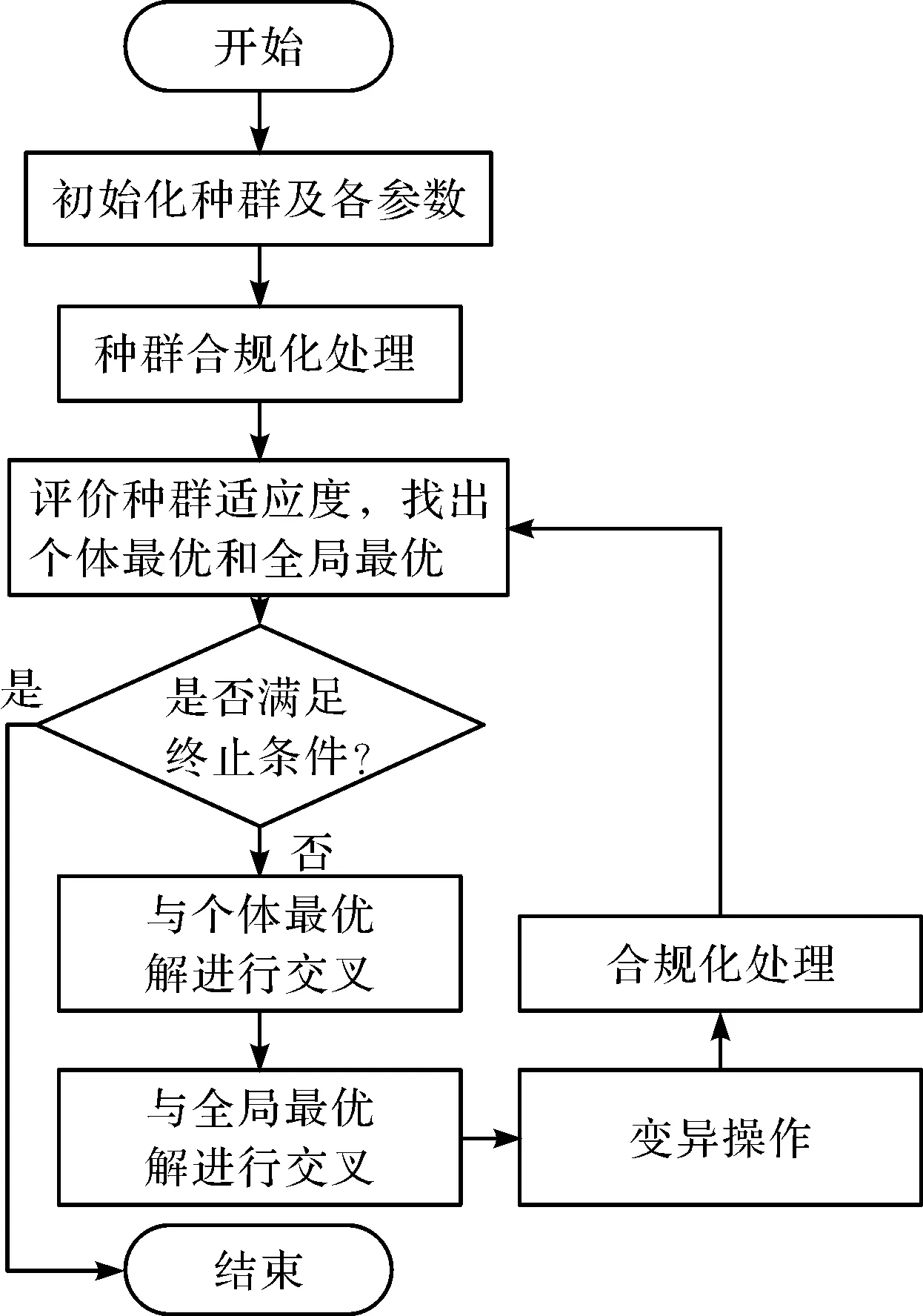
圖4 遺傳-粒子群混合算法流程圖

步驟一：設定算法基本參數(shù)，如種群數(shù)量，交叉、變異概率，粒子維度，約束矩陣，各零件拆卸的操作方向及工具信息，生成初始種群；

步驟二：對初始種群進行合規(guī)化處理；

步驟三：計算適應度，找出個體和全局最優(yōu)；

步驟四：判斷是否滿足終止條件，條件一般設定為迭代次數(shù)或者達到所要求的適應度值，若達到終止條件則結(jié)束迭代，未達到則進行步驟五；

步驟五：各個粒子先后與個體最優(yōu)解和全局最優(yōu)解進行優(yōu)先保存交叉操作，得到新的子代；

步驟七：對變異后的染色體再進行合規(guī)化處理，返回步驟三。

本文所提的混合算法主要是從用遺傳算法來模擬粒子群算法的角度出發(fā)，重構(gòu)遺傳算法交叉及變異算子。從宏觀上來看,其行為是粒子群算法；從微觀來看，其行為是遺傳算法，從而構(gòu)成遺傳-粒子群混合算法。

3 算例驗證及分析

本文所用適用于產(chǎn)品拆卸序列規(guī)劃的GA-PSO混合優(yōu)化算法由MATLAB(R2018A)編程實現(xiàn)，電腦配置為：Inter(R)Core(TM)i7- 4710MQ CPU@2.5GHz，在Windows 8系統(tǒng)下運行，算法參數(shù)主要有粒子長度lenchrom，種群數(shù)量swarmsize，最大迭代次數(shù)maxgen和約束矩陣R。

以文獻[19]中的液壓泵為例，筆者對該產(chǎn)品進行分析。該液壓泵模型包括20個最小拆卸單位。

液壓泵拆卸優(yōu)先圖模型如圖5所示。

圖5 液壓泵拆卸優(yōu)先圖

液壓泵拆卸單元信息表如表1所示。

表1 液壓泵拆卸單元信息表

算法訓練過程如圖6所示。

圖6 算法訓練過程

各算法結(jié)果對比如表2所示。

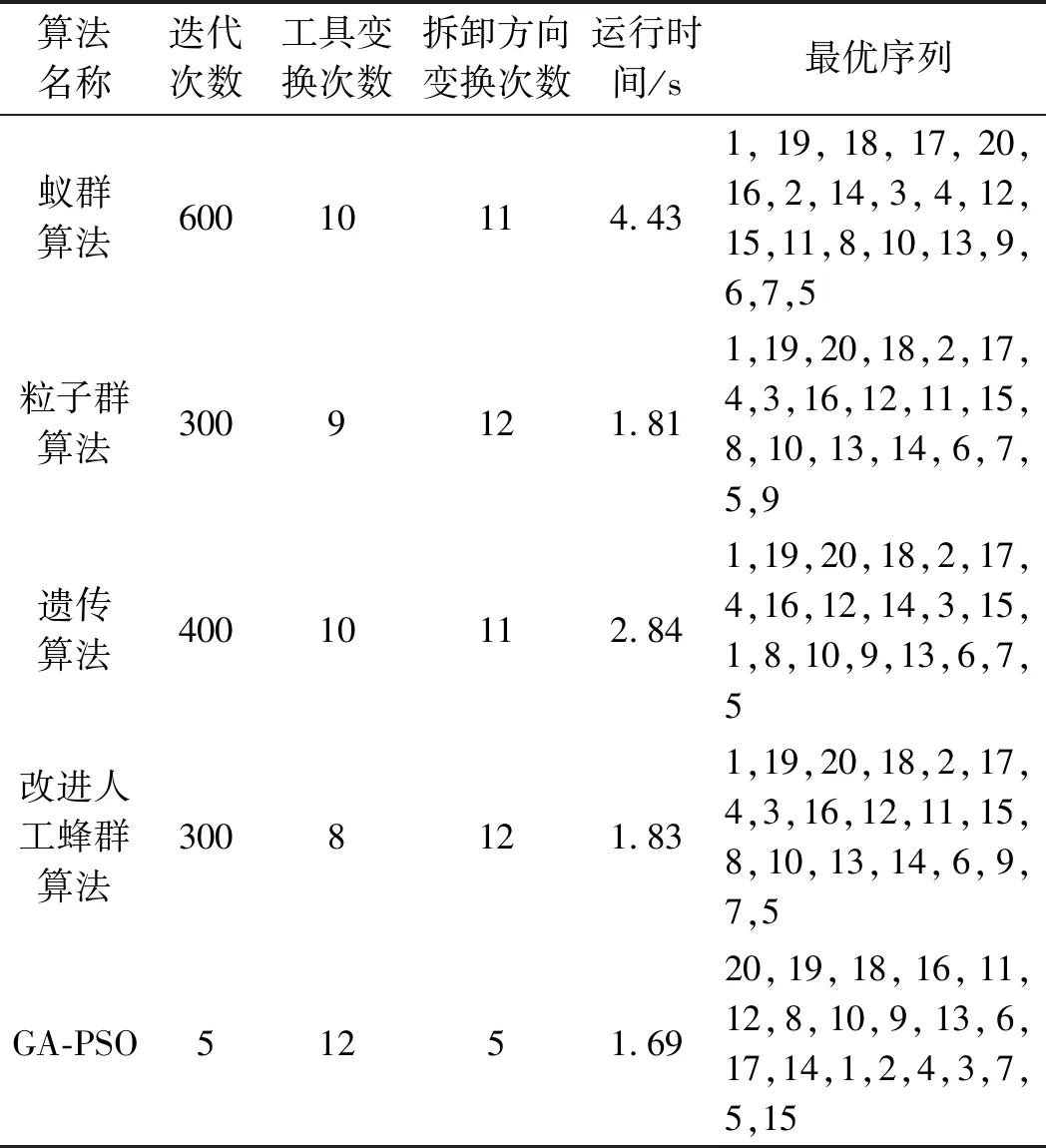
表2 各算法結(jié)果對比

由表2可知：5種算法均能得到近似最優(yōu)解，但GA-PSO算法更為優(yōu)異：蟻群算法、粒子群算法、遺傳算法、改進人工蜂群算法所得最優(yōu)解適應度分別為21、21、21、20。

與以上4種算法相比，一方面，GA-PSO算法所得最優(yōu)解適應度為17，其解更優(yōu)；另一方面，對比迭代次數(shù)與運行時間，GA-PSO的迭代次數(shù)遠遠小于以上幾種算法，且運行時間與以上算法相比較短。

綜上所述，本文提出的GA-PSO算法與其他算法相比更具優(yōu)越性。

4 結(jié)束語

DSP問題作為維修前所必須解決的問題，組合優(yōu)化極具挑戰(zhàn)性。其一是由于其在進行排列中，存在著優(yōu)先約束，使得模型的建立和算法的實現(xiàn)更加困難；其二是隨著裝配體可拆卸零件數(shù)量的增長，其排列組合將呈爆炸式增長，所以在建立模型和其求解算法時，要充分考慮這一現(xiàn)象。

本文通過拆卸優(yōu)先圖建立拆卸模型，并采用約束矩陣將模型表達為數(shù)學形式，不同于之前的研究，無需不斷對約束矩陣進行迭代更新，將其作為約束運用于后續(xù)算法，可以方便地對序列進行合規(guī)調(diào)整；運用優(yōu)先保存交叉方式和倒序式變異，對遺傳算法進行了優(yōu)化，再將遺傳算法與粒子群算法相結(jié)合，改進了粒子群算法的易陷入局部最優(yōu)的缺點。

最后，筆者以液壓泵作為算例，驗證算法的可行性及優(yōu)越性，結(jié)果證明了其具有較好的全局搜索能力以及較快的收斂速度。

在今后的研究中，筆者將著手大型裝備的多人協(xié)作拆卸序列規(guī)則；同時，此算法只適用于單人完全拆卸，筆者會在將來的研究中做進一步完善。