基于RMSprop的粒子群優(yōu)化算法
張?zhí)鞚桑钤悖椪垼顗衄?/p>
(武漢大學(xué) 計算機學(xué)院,湖北 武漢 430072)
0 引 言
粒子群算法(particle swarm optimization,PSO)[1]是由Kennedy和Eberhart提出的一種結(jié)構(gòu)簡單、收斂速度快的進(jìn)化算法。在粒子群算法中,每個解都表示為種群的一個飛行粒子,根據(jù)歷史最優(yōu)和全局最優(yōu)更新當(dāng)前位置。粒子群算法的優(yōu)點在于收斂速度快、尋優(yōu)能力強、算法簡單易實現(xiàn)。但粒子群算法容易出現(xiàn)收斂過早、陷入局部最優(yōu)的現(xiàn)象。為了解決此缺點,近些年學(xué)者提出了很多改進(jìn)思想。一類是融合其它算法提高,利用其它算法的優(yōu)勢提高其尋優(yōu)能力。文獻(xiàn)[2]中將分群策略、混沌優(yōu)化算法與粒子群算法結(jié)合,改善了算法易陷入早熟的問題。文獻(xiàn)[3]中將基于PID控制器的控制理論思想和粒子群算法結(jié)合,能夠讓粒子群算法在收斂中調(diào)整搜索方向以擺脫局部最優(yōu)。另一類是改進(jìn)算法本身,文獻(xiàn)[4]提出基于近鄰粒子交流的粒子群算法;文獻(xiàn)[5]提出了基于自適應(yīng)高斯分布的簡化粒子群算法,使用自適應(yīng)調(diào)節(jié)策略強化局部搜索能力;文獻(xiàn)[6]提出了自適應(yīng)慣性權(quán)重的粒子群優(yōu)化算法,利用粒子聚集度、迭代次數(shù)來動態(tài)改變慣性權(quán)重,以此來平衡局部尋優(yōu)能力和全局尋優(yōu)能力;文獻(xiàn)[7]提出了改進(jìn)后的自適應(yīng)慣性權(quán)重粒子群算法,利用神經(jīng)網(wǎng)絡(luò)中神經(jīng)元的非線性函數(shù)建立數(shù)學(xué)模型,提高了算法的穩(wěn)定性和收斂速度;文獻(xiàn)[8]將混沌優(yōu)化算法和粒子群算法結(jié)合,提出了一種在搜索過程中動態(tài)修正的混沌動態(tài)權(quán)值粒子群優(yōu)化算法。不同策略的改進(jìn)算法都在一定程度上提高了粒子群的收斂速度,但還是避免不了在粒子后期尋優(yōu)的過程中,隨著粒子差異性減小,收斂速度下降,無法跳出局部最優(yōu)的情況。
粒子群算法屬于優(yōu)化算法一個分支,而經(jīng)典優(yōu)化算法在近年取得了更多的發(fā)展和應(yīng)用。在機器學(xué)習(xí)[9]領(lǐng)域,經(jīng)典的梯度下降[10]算法是求解最優(yōu)化問題中最典型的方法。隨機梯度下降算法(stochastic gradient descent,SGD)源于1951年Robbins和Monro提出的隨機選擇一個或者幾個樣本的梯度替代總體梯度,從而降低了計算復(fù)雜度。后續(xù)改進(jìn)策略包括經(jīng)典動量算法(classical momentum,CM)、Nestero梯度算法(Nesterov’s accelerated gradient,NAG)[11]、Adam(adaptive moment estimation)[12]和Nadam(Nesterov-accelerated adaptive moment estimation)[13]等。文獻(xiàn)[14]將Adam算法優(yōu)化思路與粒子群位置更新相結(jié)合,提出了Adam和PSO結(jié)合的混合算法AdamPSO,使用Adam方法拓展求解空間進(jìn)行多一步搜索,提高了粒子群算法的收斂速度。因此,我們可以借鑒經(jīng)典優(yōu)化算法中的思想來改進(jìn)和拓展粒子群算法。
本文則是借鑒了在機器學(xué)習(xí)梯度下降算法中,學(xué)習(xí)率自適應(yīng)變化的思想。與粒子群算法中慣性權(quán)重的設(shè)置相結(jié)合,提出了一種自適應(yīng)慣性權(quán)重的粒子群算法(RMSPSO)。根據(jù)每個粒子每個維度的迭代變化設(shè)置恰當(dāng)?shù)膽T性權(quán)重,提高粒子的局部和全局搜索能力。通過選取對比算法在經(jīng)典的測試函數(shù)進(jìn)行驗證比較分析,結(jié)果表明本文提出的RMSPSO在大部分情況下取得了更好的結(jié)果,加快了收斂速度的同時還保持了更高的精度。
1 粒子群算法和RMSprop算法
1.1 粒子群算法
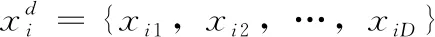
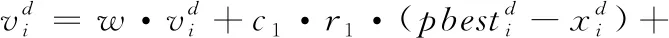
(1)
(2)
其中,ω是慣性權(quán)重系數(shù),慣性權(quán)重決定了粒子歷史飛行速度對當(dāng)前飛行速度的影響程度。c1是粒子在其歷史搜索中找到的最優(yōu)值的權(quán)重系數(shù),通常設(shè)為2;c2是粒子在群體搜索中找到最優(yōu)值的權(quán)重系數(shù),通常設(shè)為2,c1和c2通常稱為加速度常數(shù)。r1和r2是(0,1)范圍內(nèi)的兩個隨機分布值。
基本粒子群算法流程見表1。

表1 粒子群算法流程
1.2 RMSprop算法[15]
在機器學(xué)習(xí)中,學(xué)習(xí)率的選擇對最終的結(jié)果有很大的影響。太小的學(xué)習(xí)率會導(dǎo)致收斂緩慢,太大的學(xué)習(xí)率會導(dǎo)致波動增大,妨礙收斂到最優(yōu)解。目前可采用的方法是在訓(xùn)練過程中調(diào)整學(xué)習(xí)率的大小,如模擬退火[16]算法:預(yù)先定義一個迭代次數(shù)m,每迭代m次便減小學(xué)習(xí)率,或者當(dāng)適應(yīng)值函數(shù)低于一個閾值便減小學(xué)習(xí)率,然而迭代次數(shù)和閾值需要提前定義,因此無法適應(yīng)數(shù)據(jù)的特點。
在SGD和Nesterov Momentum[17]中,對于所有參數(shù)使用相同的學(xué)習(xí)率。AdaGrad算法[18,19]的思想是:每一次更新參數(shù),不同參數(shù)使用不同的學(xué)習(xí)率。如式(3)和式(4)所示。其中α是學(xué)習(xí)率,默認(rèn)值為0.001。εt是為了防止分母為0的參數(shù),默認(rèn)值為1e-6
(3)
(4)
AdaGrad在實際使用中發(fā)現(xiàn),從訓(xùn)練開始累計梯度的平方會導(dǎo)致學(xué)習(xí)率過早的減小,使得訓(xùn)練提前結(jié)束。
RMSprop為了克服AdaGrad的缺點,只累計過去w窗口大小的梯度,采用指數(shù)加權(quán)平均,如式(5)所示,ρ是指數(shù)加權(quán)參數(shù),一般取0.9
(5)
該算法更新下一位置采用式(6)所示,其中α是學(xué)習(xí)率,默認(rèn)值為0.001,εt是為了防止分母為0的參數(shù),默認(rèn)值為1e-6
(6)
RMSprop相當(dāng)于計算之前所有梯度平方對應(yīng)的平均值,可緩解AdaGrad算法學(xué)習(xí)率下降較快的問題。
2 RMSprop算法在粒子群算法上的應(yīng)用
2.1 基于RMSprop算法的粒子群算法
(7)
針對粒子群算法存在的這個問題,我們借鑒RMSprop算法的思想,提出了一種基于RMSprop算法的自適應(yīng)慣性權(quán)重取值策略。自適應(yīng)慣性權(quán)重能夠根據(jù)不同粒子不同維度的搜索信息而提供合適的取值,因此可以得到更快的收斂速度和更好的求解精度。
gij=gbesti-xij
(8)
隨著迭代次數(shù)的增加,每個粒子i都趨向群體最優(yōu)位置,則粒子i的梯度gij逐漸減小。因此,我們采用指數(shù)加權(quán)平均,采用式(9)更新當(dāng)前維度的梯度和累加∑[g2]t。ρ是加權(quán)系數(shù),取值為(0,1)之間
(9)
最后,按照式(10)更新粒子i維度j上的慣性權(quán)重ωij,其中α和β是調(diào)節(jié)系數(shù),α取值為(90,100),β取值為(0.4,0.5)
(10)
從粒子群中的某些維度的粒子來看,在迭代過程中某些粒子當(dāng)前維度全局最優(yōu)gbestj到xij的距離gij較大,粒子這一維度的慣性權(quán)重ωij就相對較大,有利于粒子探索更多區(qū)域;某些粒子當(dāng)前維度全局最優(yōu)gbestj到xij的距離gij較小,粒子這一維度的慣性權(quán)重ωij則相對較小,有利于局部挖掘。
從粒子群的粒子群體來看,在粒子群算法初期,粒子當(dāng)前維度全局最優(yōu)gbestj到xij的距離gij較大,計算的慣性權(quán)重ωij較大,有利于粒子全局探索;在粒子群算法末期,粒子當(dāng)前維度全局最優(yōu)gbestj到xij的距離gij較小,計算的慣性權(quán)重ωij較小,有利于局部挖掘,找到最優(yōu)解。從而該策略保證了粒子群的多樣性和收斂性。
2.2 算法流程
改進(jìn)的粒子群算法與基本的粒子群算法流程相似,只是在基本粒子群算法的基礎(chǔ)上,對慣性權(quán)重進(jìn)行自適應(yīng)更新,具體的算法流程見表2。

表2 RMSPSO算法流程
3 數(shù)值實驗和對比分析
為了驗證基于RMSprop算法的粒子群算法RMSPSO的收斂性能。本文選取了經(jīng)典的數(shù)值優(yōu)化函數(shù)進(jìn)行了實驗驗證,包括單峰函數(shù)、多峰函數(shù)和組合函數(shù)。同時與經(jīng)典PSO算法GPSO、經(jīng)典改進(jìn)算法LPSO、基于CAS理論的粒子群優(yōu)化算法DAPSO[20]、基于自適應(yīng)高斯分布的簡化粒子群算法IPSO3進(jìn)行對比實驗。
3.1 實驗條件及結(jié)果
數(shù)值優(yōu)化問題引入了10個數(shù)值優(yōu)化測試函數(shù)。分別是經(jīng)典的測試函數(shù)Sphere函數(shù)和Ellipsoid和CEC 2013測試函數(shù)集中的6、12、13、18、21、23、24、28號函數(shù)。分別記為f1、f2、f3、f4、f5、f6、f7、f8、f9、f10。 其中f1和f2是單峰函數(shù),f3、f4、f5、f6是多峰函數(shù),f7、f8、f9、f10是組合函數(shù)。以完整檢測算法的收斂速度、脫離局部最優(yōu)的能力和在較小梯度下的收斂能力。測試函數(shù)的定義、取值范圍和最優(yōu)解詳見表3。
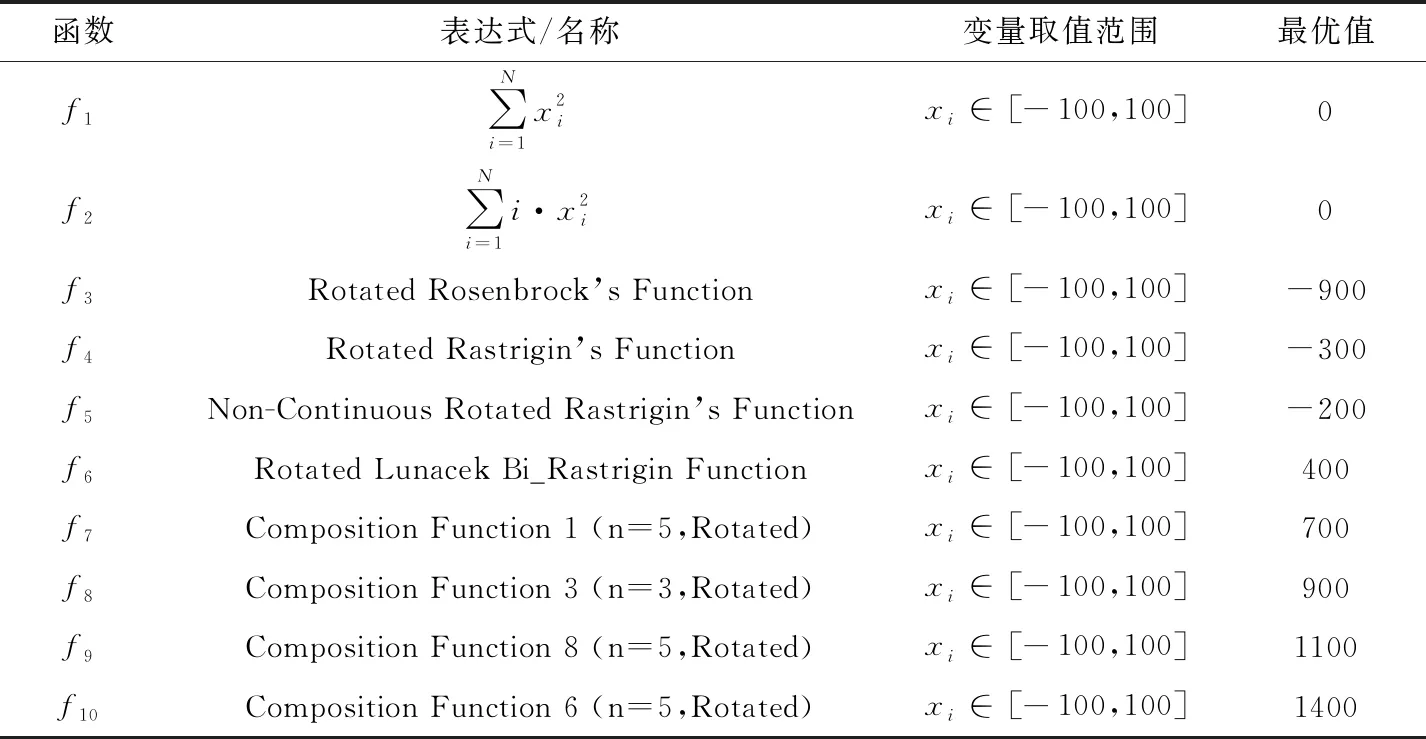
表3 數(shù)值優(yōu)化測試問題
在本節(jié)中,將RMSPSO算法和GPSO、LPSO、DAPSO、IPSO3進(jìn)行比對實驗。所有實驗的粒子種群為20,每個函數(shù)的最大迭代次數(shù)為5000。PSO慣性系數(shù)ω從0.9到0.5隨代數(shù)衰減,加速度常數(shù)c1和c2設(shè)置為2.0。LPSO的參數(shù)φ和χ采用默認(rèn)參數(shù)2.01和0.729 844。對測試函數(shù)分別在30維和50維進(jìn)行測試,每個函數(shù)獨立運行50次,記錄實驗結(jié)果的平均值和方差。
3.2 實驗結(jié)果分析
為了更加清晰、直觀觀察改進(jìn)后的粒子群算法 RMSPSO 的收斂效果,通過10個測試函數(shù)的實驗仿真圖來比較RMSPSO、GPSO、LPSO、DAPSO和IPSO3這5種不同粒子群算法的收斂情況。如圖1~圖3所示。
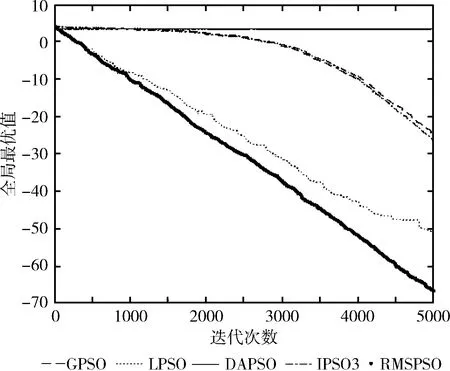
圖1 f1測試函數(shù)維度=30
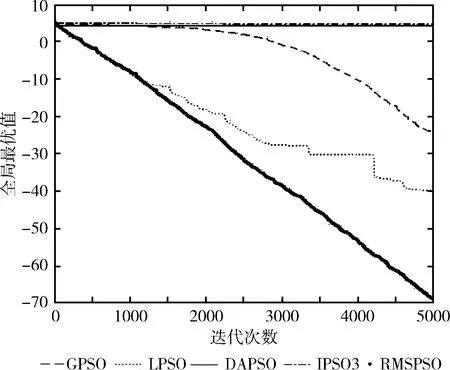
圖2 f2測試函數(shù)維度=30

圖3 f3~f10測試函數(shù)維度=30
圖1和圖2反映了單峰函數(shù)f1和f2在30維度上的實驗對比結(jié)果。通過實驗結(jié)果可以明顯發(fā)現(xiàn),RMSPSO相比GPSO、DAPSO和IPSO3可以在算法早期維持更高收斂速度,在迭代完成后,收斂精度大幅度提高。在迭代中后期,RMSPSO相比LPSO尋優(yōu)能力更強。可以得出RMSPSO在單峰函數(shù)上尋優(yōu)精度大幅提高,在算法前期、中期和后期始終保持更高的收斂速度,算法尋優(yōu)效果大幅增強。
圖3反映了多峰函數(shù)f3、f4、f5、f6和組合函數(shù)f7、f8、f9、f10在30維度上的實驗比對結(jié)果。
可知在多峰函數(shù)f3、f4、f5、f6上RMSPSO相比GPSO、LPSO、DAPSO和IPSO3大多取得了更好的收斂精度。充分說明了RMSPSO解決某些多峰函數(shù)的優(yōu)越性,跳出局部最優(yōu)能力更強。可知在復(fù)雜的組合函數(shù)f7、f8、f9、f10上RMSPSO相比GPSO、LPSO、DAPSO和IPSO3上大多也取得了更好的收斂精度,也充分說明了RMSPSO解決某些組合函數(shù)的優(yōu)越性,解決復(fù)雜函數(shù)能力更強。
算法多次運行的最優(yōu)解均值和最優(yōu)解方差是衡量算法性能的重要指標(biāo)。將GPSO、LPSO、IPSO3、DAPSO和RMSPSO分別在30維度和50維度的10個測試函數(shù)上運行50次,取平均最優(yōu)解和最優(yōu)解方差,運算結(jié)果見表4。
由表4可以看出,分別在30維度和50維度在測試函數(shù)f1~f10上執(zhí)行50次數(shù)值實驗后得到的平均值和平均方差中,30維度下RMSPSO最優(yōu)解均值取得了8個最優(yōu),最優(yōu)解方差取得了5個最優(yōu);在50維度下RMSPSO最優(yōu)解均值取得了8個最優(yōu),最優(yōu)解方差取得了7個最優(yōu)。在非最優(yōu)解的情況下,RMSPSO計算的結(jié)果與最優(yōu)解相差較小。因此可以充分支持本文提出的算法在單峰問題、多峰問題和組合問題上大部分能夠取得較好的實驗結(jié)果。與GPSO、DAPSO和IPSO3相比,結(jié)果有較大提升。在少數(shù)測試函數(shù)上,與LPSO不相上下。由此可以驗證本文提出的賦予粒子自適應(yīng)權(quán)重的改進(jìn)PSO算法增強了粒子在迭代過程中的尋優(yōu)能力,加快了算法的收斂速度,提高了算法的收斂精度。
從整體的實驗效果上看,本文提出的改進(jìn)算法RMSPSO在單峰、多峰、組合等數(shù)值優(yōu)化問題上都具備一定的適應(yīng)性。從實驗統(tǒng)計結(jié)果中平均值可以分析得出,本文提出的改進(jìn)算法RMSPSO在大部分測試函數(shù)的多個維度上可以取得更優(yōu)的計算結(jié)果,這充分說明了本文對每個粒子每個維度設(shè)置自適應(yīng)慣性權(quán)重提高了粒子的尋優(yōu)能力,從而更易跳出局部最優(yōu)找到更優(yōu)值,提高了算法的收斂能力和計算精度。從實驗統(tǒng)計結(jié)果中5個算法運行的最優(yōu)解方差可以分析得出,本文提出的改進(jìn)算法RMSPSO在具備更好的收斂能力的同時,計算結(jié)果方差更小,計算結(jié)果更加穩(wěn)定,這充分說明了本文提出的RMSPSO具備更佳的魯棒性。
4 結(jié)束語
在粒子群算法中,速度由慣性權(quán)重乘以上一代速度加上到局部最優(yōu)和全局最優(yōu)的距離更新而來,其中慣性權(quán)重ω隨迭代次數(shù)遞減。而在機器學(xué)習(xí)梯度下降算法Momentum引入了動量的概念,下一梯度由學(xué)習(xí)率乘以歷史梯度加上當(dāng)前梯度更新而來。可以發(fā)現(xiàn)兩種算法具有一定的相似性,而基于Momentum改進(jìn)算法RMSprop是一種自適應(yīng)學(xué)習(xí)率方法。因此,本文將RMSprop的自適應(yīng)學(xué)習(xí)率的設(shè)置策略與粒子群算法相結(jié)合,提出了一種自適應(yīng)慣性權(quán)重的粒子群算法RMSPSO。根據(jù)每個粒子每一維度上位置的變化設(shè)置合適的慣性權(quán)重,因此在每一代中不同粒子和不同維度的慣性權(quán)重都不同。相比原始粒子群算法,結(jié)合自適應(yīng)慣性權(quán)重的粒子群算法能夠根據(jù)粒子各個維度上的變化設(shè)置慣性權(quán)重,提高了粒子的尋優(yōu)能力。實驗結(jié)果表明,本文提出的改進(jìn)算法RMSPSO在單峰、多峰、組合數(shù)值優(yōu)化問題多數(shù)可以得到比粒子群算法GPSO、改進(jìn)粒子群算法LPSO、DAPSO和IPSO3更好的結(jié)果。這說明本文提出的改進(jìn)算法RMSPSO在提高粒子尋優(yōu)能力和加快算法收斂速度和精度上有明顯的效果。本文只是將自適應(yīng)慣性權(quán)重設(shè)置策略應(yīng)用于傳統(tǒng)粒子群算法,后續(xù)工作將著重于研究將自適應(yīng)慣性權(quán)重設(shè)置策略和其它粒子群優(yōu)化算法相結(jié)合,進(jìn)一步驗證本文提出改進(jìn)策略的普適性。

表4 粒子群算法在30維和50維的f1~f10測試函數(shù)上的實驗結(jié)果

