基于核主成分分析的超多面體數據描述方法
陳宇晨,何毅斌,戴喬森,劉 湘
(武漢工程大學 機電工程學院,湖北 武漢 430205)
0 引 言
標注出正常數據中的異常數據的問題稱為異常檢測[1],通常檢測任務中只有一類樣本充分采集,而另一類欠采樣[2-4],目前處理這一類特殊問題最常用的方法為基于數據描述的方法[5]。基于數據描述的方法主要指支持向量數據描述法及在其基礎上改進和補充的方法,這些改進和補充的方法包括:利用現代優化方法對懲罰項系數和核寬度參數優化[6,7],對核方法采用擴展策略[8]以及組合多種核方法[9,10],使用其它距離表示方式代替歐式距離[11,12]等,然而這些方法無論怎樣改進和補充,均無法改變其本質是通過在高維空間中訓練一個超球體支撐域來描述數據,若訓練樣本在線性空間中極度不符合超球體時,將會產生較大分類誤差。
為了給數據描述類方法提供另一種支撐域形狀,在訓練樣本不適合使用支持向量數據描述方法時有更多的方法選擇,本文提出一種基于核主成分分析超多面體數據描述的方法,該方法首先使用核方法對訓練樣本進行非線性映射,再利用非線性映射后樣本的主成分信息構造超多面體分類器,解決了主成分分析僅能對數據線性表示的局限,實現對樣本的異常檢測。與支持向量數據描述法相比,超多面體具有更多的訓練參數,在某些分布下,超多面體比超球體支撐域的描述更加符合訓練樣本。
1 多面體數據描述模型建立
1.1 問題描述及模型評價方法
異常檢測問題往往可以得到大量的正常數據,異常數據出現的概率非常低,然而異常數據一旦產生,且未被正確識別將會造成很大的不良影響[13,14]。通常對未標記錯誤的數據進行監督學習會產生不錯的模型,但數據中若混有錯誤標記的數據往往降低模型精度,因此本文主要對擁有標記樣本以及標記樣本中混有異常數據的情況建模,即對樣本進行監督學習。
由于樣本的不平衡性,以準確率作為評價標準的方法并不適用此類問題,對于這類問題需要同時考慮第一種誤差和第二種誤差。預測結果和真實結果的混淆矩陣見表1。

表1 混淆矩陣
定義精確率為P、召回率為R計算公式分別如下所示
(1)
F1分數定義為準確率與召回率的加權平均
(2)
精確率P代表正確被檢索的占所有實際被檢索到的比例,召回率R代表正確被檢索的占所有應該檢索到的比例,F1分數為兩者的調和平均數,F1分數越大,表示分類正確的數量越多,當F1分數為1時,表示分類完全正確[15]。
1.2 多面體數據描述模型建立
N維空間中的一組數據可以由y1…y2N,共2N個超平面形成的超多面體支撐域完全包圍,其中
(3)
式中:wi——超平面的法向量,bi——超平面的常數項。
每個yi可視為一個線性分類器,且總存在兩個不同的超平面擁有相同的法向量wi,分別將其稱為下界分類器與上界分類器,對于新的樣本點xi,若其屬于正常類,應滿足
(4)
二維空間中一組樣本的平行四邊形支撐域如圖1所示。

圖1 二維空間四邊形支撐域
圖1中y2、y4為下界分類器,y1、y3為上界分類器,4個分類器組合成為一個平行四邊形,當新的樣本點xi落在四邊形內部時則判定其為正常樣本,反之則為異常樣本。
對高維空間每個下界分類器ym,若已知法向量wm,bm的值可以通過以下約束優化問題求解
(5)
式中:xi——某個樣本點,εi——松弛變量,C——自定義量。
與ym對應的上界分類器yn,其法向量與上界分類器的wm相同,常數項bn的值可以通過以下約束優化問題求解
(6)
由于無法保證用于訓練模型的數據全為正常樣本,為減少異常樣本的影響可以調整式(5)、式(6)中εi以及C的值。
調整C的值對分類器的影響如圖2所示。

圖2 調整參數C的影響
圖2為組一維數據,數據多集中在中央,中間的密度很大,向兩側密度逐漸降低,密度很低的點為異常樣本的可能性大,通過逐漸減小C,越來越多的低密度點被排除,即起到了排除訓練數據中異常樣本的作用。
若認為用于模型訓練的樣本中有較多異常樣本,可將C設定較小,反之則給C較大的值。
2 主成分分析及模型簡化
對法向量wi的選擇直接影響模型,本文使用主成分分析方法計算法向量wi,主成分分析法主要用于提取數據的主要特征,利用數據協方差矩陣的特征向量作為法向量wi,wi包含了數據間的相關信息,利用此作為法向量,得到的超多面體恰好符合數據各個方向的變化趨勢。
2.1 主成分分析
主成分分析的主要思想是將空間中一組具有相關性的數據,使用其協方差矩陣的特征向量組成的基,表示原數據的坐標,消除數據間的相關性,也可將數據投影到部分特征向量組成的子空間中,實現數據的降維[16]。
主成分分析方法可以通過下面的步驟實現:
(1)計算數據每個特征的平均值μ=(μ1…μn);
(2)利用平均值μ計算數據的協方差矩陣
(7)
(3)對協方差矩陣進行特征值分解
∑=QΛQ′
(8)
其中,Q為特征向量組成的矩陣,Λ為特征值組成的對角矩陣;
(4)數據投影到N個特征向量構建的子空間
Xnew=QX
(9)
2.2 模型簡化
假設特征向量組成的矩陣為:Q=(Q1,…,Qn),分別利用Qi作為模型的法向量wi,將空間中所有的數據投影到以Qi為基的一維子空間中,此時所有的數據退化為標量,訓練的參數為超平面的平移量b′m,對下界分類器,b′m的值可以通過以下約束優化問題求解
stxi+εi>b′m
εi≥0
(10)
對應上界分類器平移量b′n通過以下約束優化問題求解
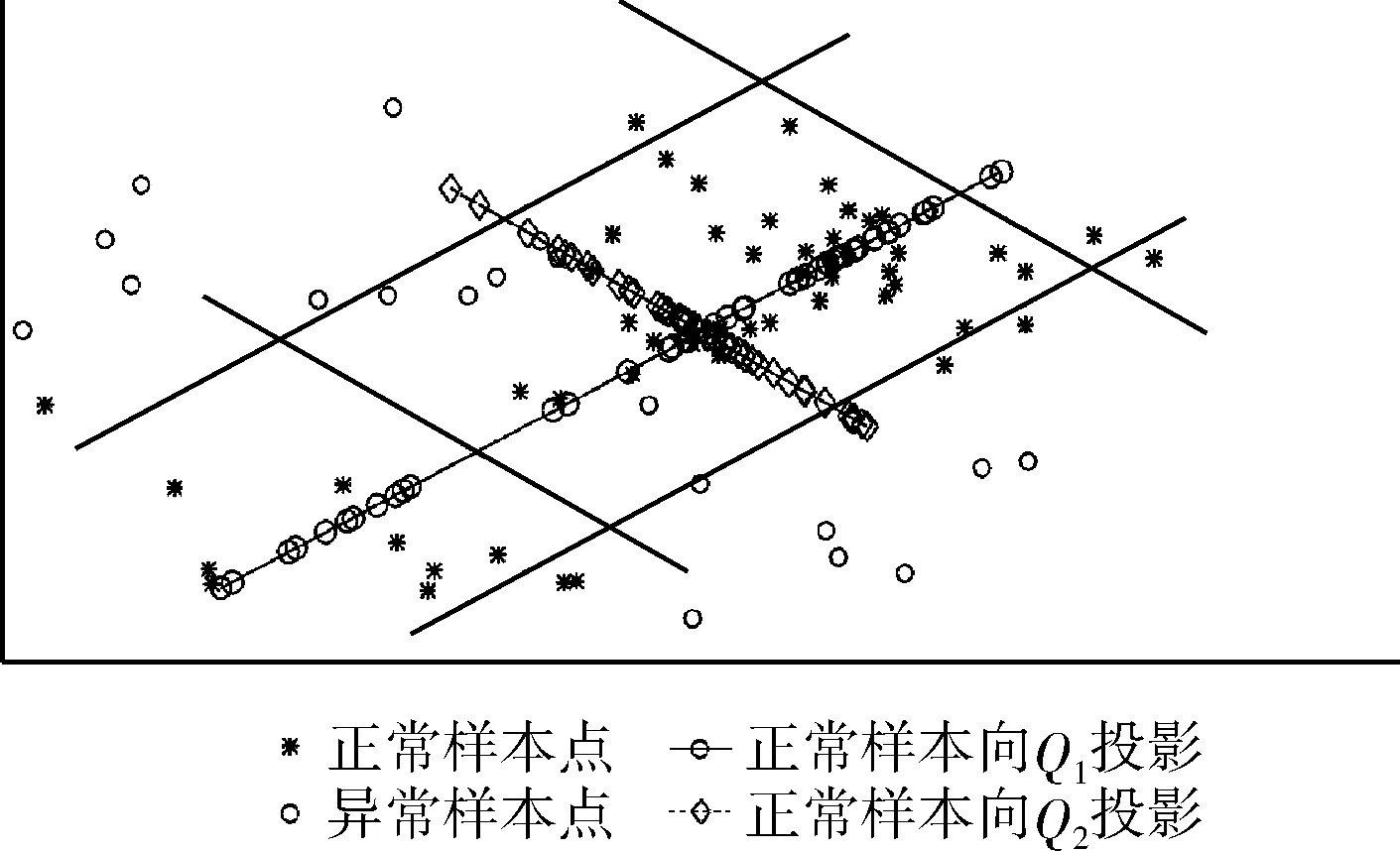
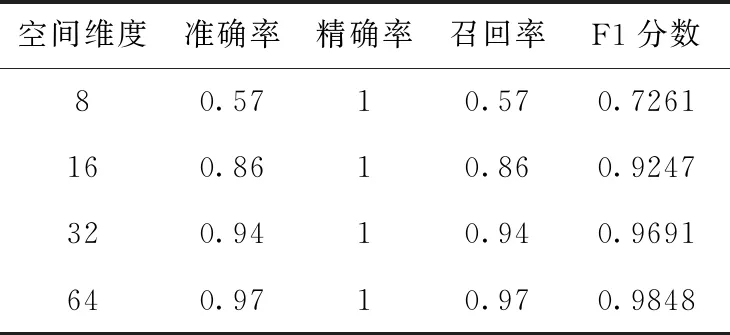
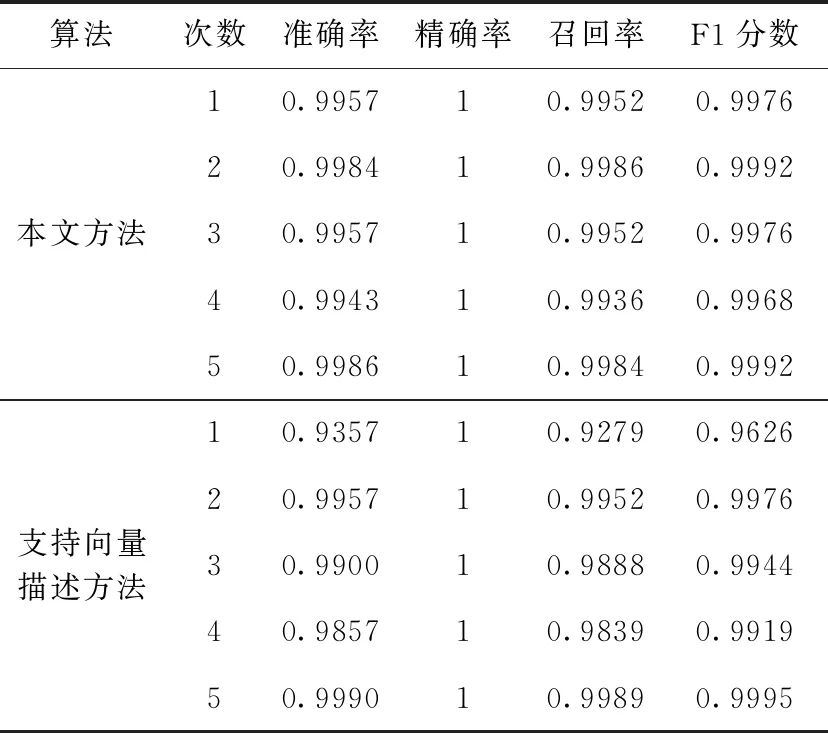
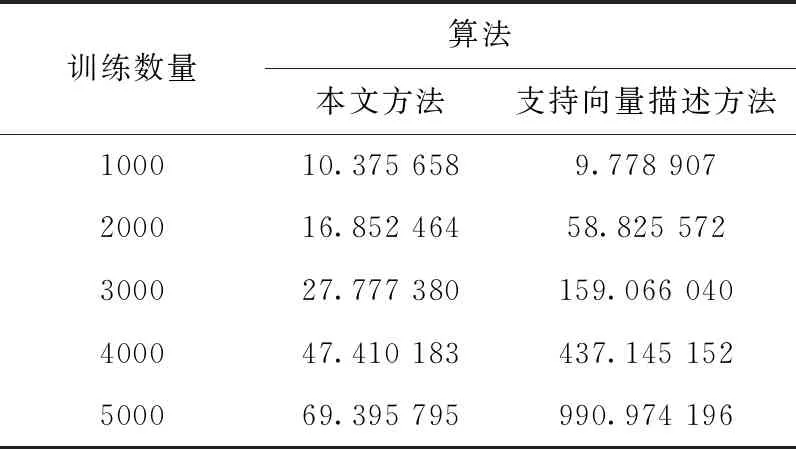
stxi-εi εi≥0 (11) 上式與式(5)、式(6)相比,約束優化問題的求解難度降低。 二維空間一組數據,協方差矩陣特征向量為Q=(Q1,Q2),數據向每個特征向量的投影及支撐域如圖3所示。 圖3 主成分方法訓練支撐域 圖3中,使用主成分法將數據分別投影到基為Q1和Q2的一維子空間中,并訓練簡化后的約束優化模型,得到的平行四邊形支持域可以很好描述原數據,表明利用主成分的方法簡化以及求解模型的有效性。 簡化后的約束優化模型的平移量b′m、b′n與原模型的常數項bm、bn間的關系滿足 (12) 式中:Qi——模型的法向量,但是由于式中絕對值的影響,導致了bm、bn均會求解出雙值,為了避免在高維空間中對多個結果的討論,所以采用將新數據投影到其特征向量為基底的線性空間中判斷其是否為正常數據的策略,而不是顯式求解出2N個超平面的方程。 主成分分析簡化模型求解,并計算出法向量wi,但因為其線性特性,往往無法處理非線性數據,導致這類數據最后得到的支撐域判決效果很差,一組以異或方式分布的數據及其向特征向量投影及支撐域如圖4所示。 圖4 非線性可分數據的支撐域 圖4中,兩種數據不可被線性分離,以一種異或狀態分布,使用主成分分析法建立平行四邊形支撐域導致了大量異常數據被誤分類。 為了解決這個問題,在主成分分析的基礎上引入核方法,核方法以一種非線性映射的方式將數據投射到一個高維的特征空間里,不僅改變了數據的維度,而且使數據的某一特征得到保留甚至強化得到更好的分類效果[17]。 設Φ(·)為向高維空間的映射,對協方差矩陣的特征分解可以表示為 (13) 式中:x——數據矩陣,μ——數據矩陣特征的均值,ωi——Φ(X)Φ(X)′的特征向量,λi——特征值。 核主成分分析的一個重要定理表明:空間中的任一向量都可以由該空間的所有數據線性表示,將特征向量ωi利用數據集合Φ(X)線性表示 ωi=Φ(X)α′ (14) 式中:α——線性組合的系數向量。 將式(14)帶入式(13),在等號兩側同時左乘Φ(X),得到 Φ(X)′Φ(X)Φ(X)′Φ(X)α=λiΦ(X)′Φ(X)α (15) 式中:Φ(X)′Φ(X)用中心化的Gram矩陣Kc代替,即 (16) 由于矩陣Kc為正定對稱矩陣,所以存在逆矩陣,上式可進一步簡化為 Kcα=λiα (17) Kc可用Gram矩陣K表示 Kc=K-KE-EK-EKE (18) 式中:E——所有元素均為1/n的Rn×n的矩陣。 計算Gram矩陣常用的核函數包括:線性核函數、多項式核函數、高斯核函數,其表達式分別為 (19) 式中:p、σ——核的大小,屬于自定義量。 一般情況下,高斯核是合理的首選。第一,對比線性內核,非線性內核映射數據進入一個更高維空間,可以處理類別標簽和屬性之間的非線性的關系,第二,超參數的數量會影響模型選擇的復雜性,而多項式內核的超參數多于高斯核,最后,高斯核將向量間的內積映射到0-1之間,而多項式核可能將向量內積映射到無窮。 (20) 將上文異或條件下的數據利用核主成分分析投影到新的二維平面上,其中核函數選擇高斯核函數,新數據的位置和訓練的支撐域如圖5所示。 圖5 核主成分分析得到的坐標及支撐域 利用核主成分分析將異或狀態數據中正常數據投影到不同的高維線性空間中并訓練模型,再將異常數據帶入模型測試,其準確率、精確率、召回率以及F1分數見表2。 表2 各維度下各項指標 圖5和表2表明在高維線性空間,異或分布的數據各項指標均值均較高,說明了核方法的有效性,將線性不可分的數據在高維空間下變的可分,訓練出了有效的超多面體支撐域。 核主成分分析超多面體數據描述方法的步驟如圖6所示。 圖6 核主成分分析超多面體數據描述方法步驟 本文采用mulcross數據集進行實驗,該數據集共有235 930組正常數據及26 214組異常數據,每個數據包括4個特征,其分布特征如圖7所示。 圖7 數據分析盒須圖 圖7表示了數據集每個特征的數據分布范圍、數據的中位數、上四分位數和下四分位數以及異常數據值。 使用matlab 2015b測試本文方法,dd_tools工具箱構造支持向量描述方法。從數據集的正常數據中不放回抽取5000組正常數據作為訓練集,再從剩余包含正常和異常數據的數據中抽取1000組數據作為測試集,改變空間維度,記錄空間維度數及準確率、精確率、召回率、F1分數,結果見表3。 表3 本文算法各維度下分項指標 表3表明空間維度選擇4以上時可以得到不錯的分類效果,因此本文實驗中的空間維度選擇4維。 重復上述方法抽樣5次,使用本文算法及支持向量描述方法利用同樣的數據訓練模型、測試模型,本文算法使用粒子群算法求解約束優化,兩種方法均選用高斯核函數,結果見表4。 表4 兩種算法分類指標結果 表4表明在所有訓練數據均為正常時,本文的方法與支持向量描述方法都可以得到非常好的分類效果,且精確率均為1,說明分類時沒有犯第二類錯誤,即沒有將異常數據分類為正常數據,驗證了本文方法的有效性。 當在選擇訓練集數據時,不放回的抽取N組異常數據以及5000-N組正常數據作為訓練集,再從剩下的數據中抽取1000組作為測試集數據,當N取不同值時兩種算法各項指標結果見表5。 表5 加入異常數據后兩種算法分類指標結果 將表5繪制為折線圖比較兩種方法,折線如圖8所示。 表5和圖8表明兩種方法的精確率均為1,分類結果均沒有發生第二類錯誤,有效防止了第二類錯誤產生的不良后果,本文的方法除精確率以外的各項指標會隨著異常數據混入的越來越多而下降,但即使在數據中混入10%的異常數據,依然可以得到較好的分類結果,在數據中混入2%的異常數據時,準確率依然可以達到0.945,F1分數達到0.9717,實驗結果上看混入異常數據的情況下本文方法各項指標高于支持向量描述方法,驗證了本文方法的穩定性。 圖8 兩種算法混入異常數據時各項分類指標 為了比較本文的方法與支持向量數據描述方法的時間差異,取訓練集的數量為1000~5000,取樣間隔為1000,記錄每次訓練的時間,結果見表6。 表6 兩種算法時間比較/s 表6表明當訓練數據的數量較少時,支持向量描述方法的訓練時間略少于本文的方法,但隨著訓練數據的增加,支持向量描述方法需要的訓練時間也隨之迅速增長,當訓練數量達到5000時,本文法的訓練時間不到支持向量描述方法的1/10。 將該方法與支持向量描述方法應用到ODDS數據集中的thyroid數據集(共3772組數據,數據維度為6,93組離群數據),wbc數據集(共278組數據,數據維度為30,21組離群數據)、vomels數據集(共1456組數據,數據維度為12,50組離群數據)、ecoli數據集(共336組數據,數據維度為7,9組離群數據)中,兩種方法的各項指標如圖9所示。 圖9 4種不同數據集兩種方法測試 圖9表明4種不同數據集測試下本文方法的效果均好于支持向量數據描述方法,利用更多的數據集再次驗證了本文方法在異常檢測中的可行性和有效性。 本文研究了基于核主成分分析的超多面體數據描述方法,用于解決數據中正常異常樣本分布不均勻的情況下的異常檢測問題,與支持向量數據描述方法相比較,本文方法不再局限于使用超球體對數據進行描述,而是為數據描述類的方法提供了另外的支撐域形狀。通過實驗發現,當訓練數據中的樣本量增多時,本文方法的時間復雜度并不會急劇上升,在一些數據集上可以得到比支持向量描述更好的分類效果,即使訓練數據中混有部分異常數據時也具有一定的穩定性。
3 核方法下的超多面體非線性描述
3.1 主成分分析的局限性
3.2 核主成分分析
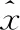



4 實例分析





5 結束語

