基于L2,1-范數距離的約束相似矩陣的聚類算法

張 要，馬盈倉，楊小飛，朱恒東，楊 婷

(西安工程大學 理學院，陜西 西安 710600)

0 引 言

在過去的幾十年中，大量的聚類方法得到了廣泛的發展，并取得了令人矚目的成就[1,2]。文獻[3,4]將聚類分析的方法分為以下幾類：基于密度的聚類、劃分法聚類、基于網格的聚類、基于模型的聚類、層次法聚類、基于圖論的聚類。

近些年來，聚類算法得到廣泛的研究。學者們也發現：在聚類算法中相似度矩陣的構建是重要而基礎的，對聚類結果起決定性作用[5]。所以學者們紛紛圍繞如何構建更好的相似度矩陣展開研究。

經典譜聚類[6]算法使用了傳統的高斯核函數來構造相似矩陣；文獻[7]為消除噪聲的影響，從數據自身特性出發來構造相似度矩陣，提出了一種基于自然最近鄰相似圖的譜聚類算法(NSG-SC)；文獻[8]利用歐式距離將數據集劃分為若干個子集，計算其協方差，并利用設定閾值來剔除交叉點，用剔除交叉點后的新數據集來學習相似度矩陣，最后用K-Means對特征分解后的相似度矩陣進行聚類，提出了基于局部協方差矩陣的譜聚類算法。文獻[9]在經典譜聚類的基礎上進行改進，在無向圖數據構成鄰接矩陣的基礎上，利用SimRank計算數據集的相似度矩陣，提出了一種基于SimRank的譜聚類算法；文獻[10]提出了一種自適應模糊聚類算法(AFCM)，AFCM算法中構造的觀察矩陣、判斷矩陣和集合劃分可以自動確定合適的聚類數，為得到更好的圖像分割效果，采用核距離作為相似性度量；文獻[11]提出了區間模糊譜聚類圖像分割方法，該方法通過區間模糊隸屬度構造的區間模糊相似性測度來學習相似度矩陣，并通過規范切圖譜劃分準則對圖像進行劃分，得到最終的圖像分割結果；文獻[12,13]提出構建一種無參數相似圖，即密度自適應鄰域(DAN)，它結合了距離、密度和連通性信息，反映了數據集的局部特征。

文獻[14]利用距離指數變換函數和稀疏化算法構建了分塊對角矩陣以重新解釋樣本之間的相似度；文獻[15]根據核參數和共享近鄰點的個數計算所有樣本點之間的相似度并進行聚類。文獻[16]通過改進傳統譜聚類中的度量方式，用基于傳遞距離的度量方式度量樣本間相似性；文獻[17]利用密度差來調整樣本點之間的相似度構造新的相似矩陣函數；文獻[18]運用共享近鄰來度量不同數據之間的相似程度，并利用兩數據點間的主動約束信息找到他們的關系；文獻[19]利用有向連接矩陣作為新的相似性度量方法；文獻[20]提出一種以HowNet語義詞庫和BTM主題建模為基礎的相似度計算方法，將兩者進行線性組合，綜合考察文本的相似性。文獻[21]運用冪高斯核函數來求解不同數據點間的相似性，但該算法比較依賴先驗信息，沒有先驗信息的話，就難以找到合適的參數來調節鄰域尺度。

然而，許多改進后的算法仍是基于平方歐式距離來學習相似度矩陣的，如Fuzzy K-Means(FKM)[22]、CLR_W[23]、CAN[24]等。眾所周知，雖然使用平方歐式距離較為方便，但卻不如L2,1-范數距離更具有魯棒性[25]。二次損失函數對異常值不具有魯棒性。為了克服這個缺點，應該用一個對異常值不敏感的二次損失函數來代替，例如L2,1-范數。

關于算法的魯棒性問題，CSCA算法使用了基于L2,1-范數距離的目標函數。基于“L2,1-范數”距離，它不是平方的，通常用于誘導稀疏性，與平方歐式距離相比，離群值對聚類結果帶來的影響更小。考慮到用L2,1-范數距離代替平方歐式距離可以減小離群值對聚類結果帶來的影響，但同時也對噪聲比較不敏感。所以，本文對相似度矩陣的施加平方的約束。并且本文在優化算法上采用K鄰近法來消減噪聲帶來的影響。最后在學習相似度矩陣的過程中，約束相似度矩陣的拉普拉斯矩陣的秩，因為這種約束，所以也能起到直接聚類的效果。并且本文對合成數據集和一些真實數據集進行了實證研究，來驗證本文提出的方法。本文所希望的實驗結果是——本文給出的通過約束基于L2,1-范數距離的相似度矩陣的聚類方法，在大多數情況下都優于其它相關的聚類方法。

1 新模型的建立與求解

1.1 已有模型

經典譜聚類算法[26]的基本思想是，距離較遠的兩個點之間的邊權重值較低，而距離較近的兩個點之間的邊權重值較高，不過這僅僅是定性，而譜聚類則需要定量的權重值。所以，譜聚類利用樣本點間的距離得到的相似度矩陣S來學習鄰接矩陣W。關系式是使用廣泛使用的自調高斯方法來構造親和矩陣(σ的值是自調的)[26]

(1)

在學得鄰接矩陣W后，經典譜聚類算法會通過解決問題(2)來進行數據處理

minTr(FTLWF)s.t.FTF=I

(2)

最后，大多數譜聚類算法[27]通過在F上運行K-Means算法，來獲得最終的聚類結果。但K-Means對F要求很高，這使得聚類性能不穩定。

在文獻[23]中給出了CLR_W的初始數據圖的學習方法，目標函數為

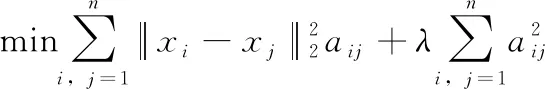
(3)

文獻[28]是學習一個數據-錨點二部圖(其中邊的權重表示對應的數據與錨點的相似度)，并基于二部圖完成快速聚類的。其目標函數為

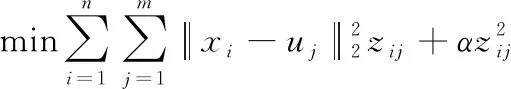
(4)

可以發現，無論譜聚類、CLR_W、CAN，還是K-Means都是基于平方歐式距離的聚類，從而會出現不夠魯棒性的問題。本文為了減小離群值對聚類結果帶來的影響，采用更具有魯棒性的L2,1-范數距離來進行初始數據圖的學習。

1.2 L2,1-范數

關于矩陣的L2,1-范數在文獻[29]中作為旋轉不變的L1-范數首次引入，并給出了L2,1-范數的定義。L2,1-范數也被用于多標簽特征選擇[30]和Group Lasso[31]。

在文獻[32]中指出，L2,1-范數對于行來說具有旋轉不變性，其中R是任意的旋轉矩陣。并將L2,1-范數推廣到Lr,p-范數

(5)

式中：M∈Rn×m；mi表示矩陣M的第i行向量；mij表示矩陣M的第i行，第j列的元素。

而對于向量mi來說

(6)

1.3 確立相似度矩陣

考慮到利用相似度矩陣的平方，來約束相似度矩陣，可以放大不同數據點間的相似度差異；同時，采用K鄰近法，也可以一定程度上消減噪聲對聚類結果的影響。

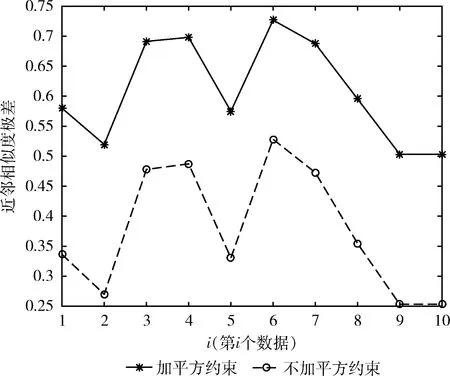
圖1 是否加平方約束對相似度差異的影響

從圖1中可以看出，實線始終在虛線的線上方，這說明對相似度矩陣加以平方的約束，可以放大不同數據點間相似度的差異，從而能夠更好的對數據點進行聚類。

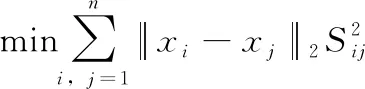
(7)

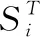
1.4 確立目標函數

由于該算法學得的相似度矩陣S是非負的，所以如果可以直接學習到恰好具有c個連接分量的結構化圖，就可以不使用離散化步驟。在文獻[28]指出，若相似度矩陣S是非負的，則歸一化拉普拉斯矩陣LS有如定理1所示的重要性質。

定理1[28]歸一化拉普拉斯矩陣LS的特征值為0的重數等于與S所對應的圖中連通分量的數目。

所以，本文對學得的相似度矩陣的拉普拉斯矩陣施加約束條件：rank(LS)=n-c，從而得到聚類算法的目標函數

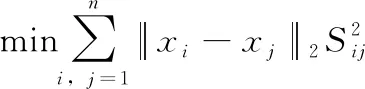
(8)

式中：LS表示S的拉普拉斯矩陣，且LS∈Rn×n。

1.5 求解目標函數

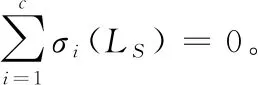
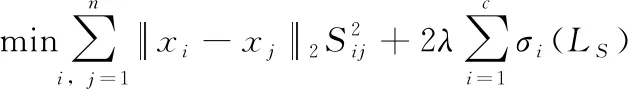
(9)

根據Ky Fan定理[33]，可得

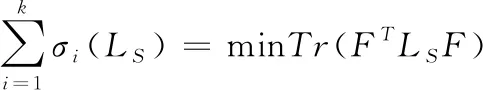
(10)

所以式(9)可以寫成

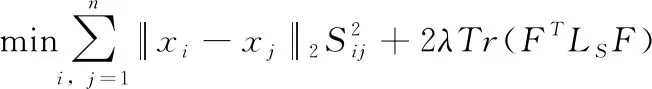
(11)

相對于式(8)而言，式(11)較容易解決。如果固定S，那么式(11)等價于

min2λTr(FTLSF)s.t.FTF=I

(12)

這里F的符合約束條件的F的最優解，就是LS矩陣的前c個最小特征值組成的特征向量。當然，在這可以用K-Means去處理F的最優解，這樣也能得到聚類結果。

根據拉普拉斯矩陣的性質

(13)

式中：fi與fj分別表示F的第i行與第j行的向量。

如果F被固定，那么式(11)可以轉化為

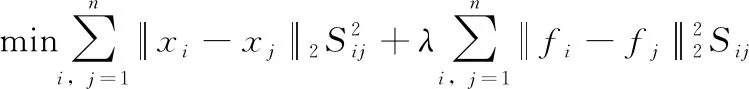
(14)

(15)

由于式(15)對于不同的i之間是相互獨立的，所以對于每個i，式(15)都可以寫成

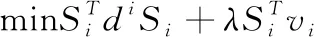
(16)

式中：vi是矩陣V的第i行向量，di是距離矩陣D的第i行向量寫成的對角矩陣，即

(17)

利用拉格朗日乘子法，可以將式(16)寫成

(18)

式中：α與βi均是拉格朗日因子，且有α≥0、βij≥0。

關于式(18)，對Si求偏導，并令導函數的值為0，可得

(19)

對每個i而言，可以將式(19)寫成

(20)

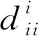
根據KKT條件[34]可知Sijβij=0，所以式(20)可以寫成

(21)

從而計算出

(22)

其中

(23)

從而，可以定義函數gi(α)

(24)

gi(α)=0

(25)

因此，α的值是函數gi(α) 的根。需要注意的是，gi(α) 是一個分段線性單調遞增的函數，因此用牛頓迭代法可以很容易地求出根。計算α后，由式(22)得到式(14)的最優解。

CSCA具體算法如下：

輸入： 特征矩陣F，聚類數c，足夠大的λ，近鄰參數k。

輸出： 聚類結果y。

(1)計算數據點間的距離矩陣D。

(2)初始化特征矩陣F。

(3)對距離矩陣D的每行排序。

(4)設置迭代。

for j=1,2,…,n do

定義相似度矩陣S∈Rn×n。

(5)更新新相似度矩陣S。

for i=1,2,…,n do

找出，第i個數據點的k近鄰。

找出，k近鄰所對應的vij。

對每個i，根據求解式(16)來更新相似度矩陣的Si。

end for

(6)更新特征矩陣F。

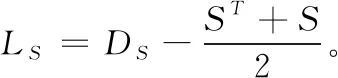
(7)設置跳出迭代條件，并用二分法調節參數λ的值。

(8)通過求圖的連通分支直接得到聚類結果y。

end for

2 實驗與結果

為體現本文所提出的聚類算法CSCA的可行性，選取了經典聚類算法：K-Means算法、RCut算法、NCut算法；經典子空間聚類算法：SR算法、LRR算法；以及經學者改進的算法：CLR_W算法、CAN算法，作為對比算法。并且采用準確率(Accuracy，ACC)、標準化互信(norma-lized mutual information，NMI)[35]等多種評價指標對聚類結果進行評價。

在參數方面，由于K-Means算法的不穩定性，對于 K-Means 算法、SR算法、LRR算法，采用運行10次取最大值的方法。對于RCut算法和NCut算法，實驗使用了廣泛使用的自調高斯方法來構造親和矩陣(σ的值是自調的)。對于CLR_W算法與 CAN算法，實驗使用了文獻[23]中給出的初始數據圖的學習方法，而CLR_W算法與CAN算法中的參數λ是自調的。對于CSCA算法中的參數λ與近鄰參數K，其中參數λ是自調的，近鄰參數K的取值為3～10。

在實驗環境方面，本文所有的實驗相關環境為：Microsoft Windows7系統，處理器為：Intel(R) Core(TM) i5-4210U CUP @ 1.70 GHz 2.40 GHz，內存：4.00 GB，采用編程軟件為：Matlab R2016a。

2.1 人工數據集實驗

在人工數據集的實驗上，采用人工雙月數據集進行實驗。人工雙月數據集是由2個集群構成的數據集，其中每個集群包含200個2維數據點為樣本。雙月構成的圖形如圖2(a)所示。噪聲百分比設置為0.1。近鄰參數K設置為9。實驗的目標是在學習相似矩陣的同時，通過約束相似矩陣的拉普拉斯矩陣的秩，使相似矩陣中剛好有2個連通分量。用CSCA進行了測試，取得了較好的效果。在圖2(a)中，數據的原始圖呈現雙月狀，讓連線的寬度表示兩個對應點的親和力。從圖2(b)中可以很容易地觀察到本文提出的聚類算法CSCA的有效性。

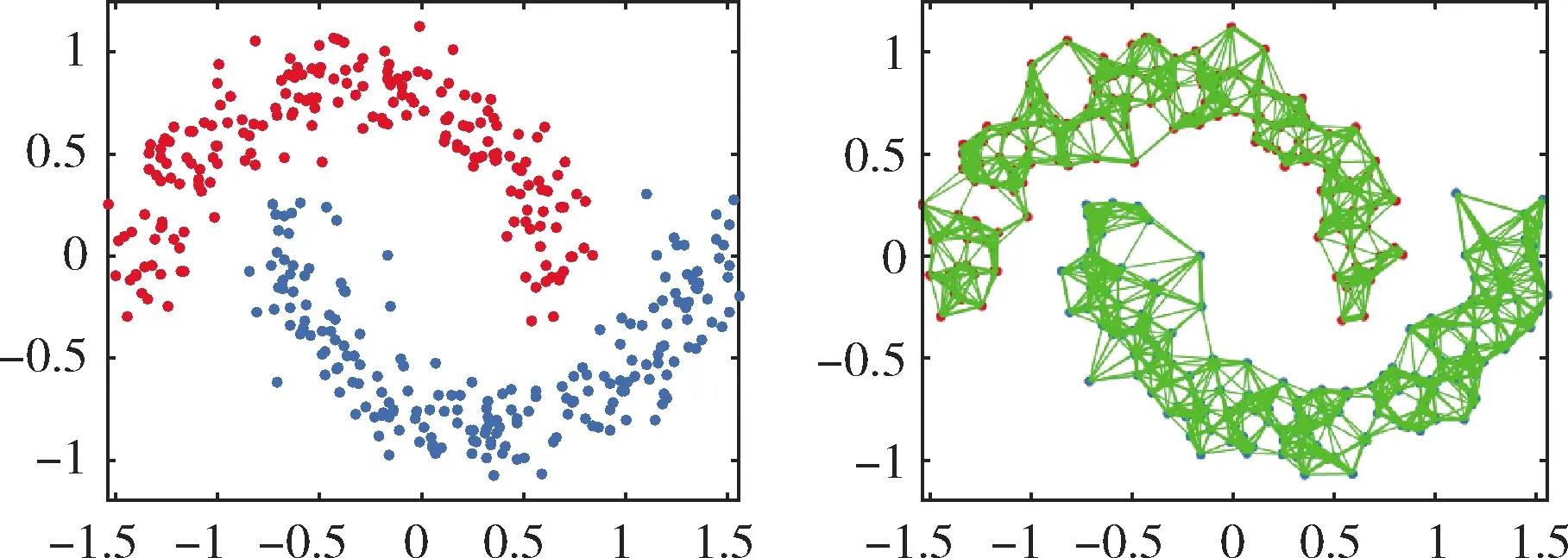
圖2 雙月數據原始圖像與聚類結果

此外，實驗還采用人工螺旋數據集Spiral進行實驗。人工數據集Spiral是由3個集群構成的數據集，其中每個集群包含104個2維數據點為樣本。Spiral構成的圖形如圖3(a) 所示。噪聲百分比設置為0.1。近鄰參數K設置為3～8。在圖3(a)中，可以看出數據呈現螺旋狀，由3條點線螺旋組成，每條線為一個集群。圖3(b)則是聚類算法CSCA的聚類結果。

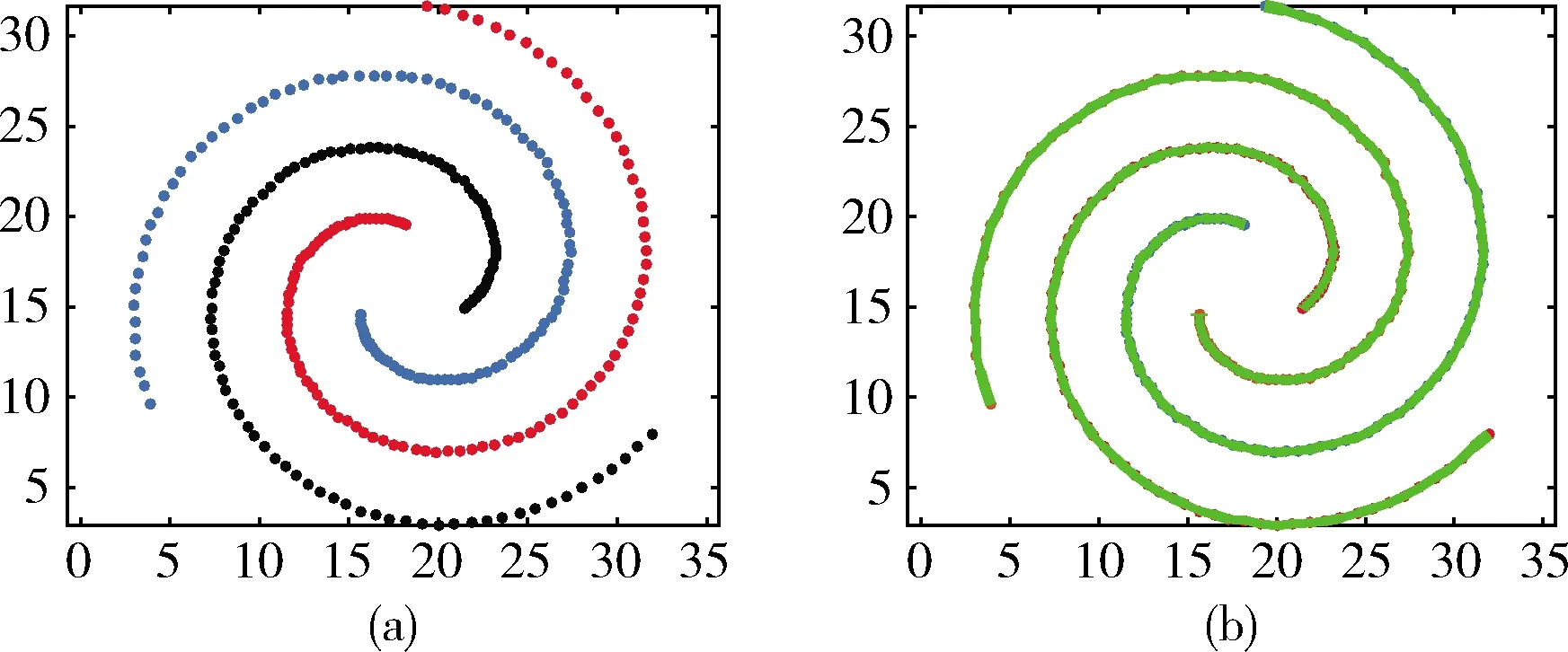
圖3 Spiral原始數據與聚類結果

同時本文還分析了，在雙月數據集與Spiral數據集上，近鄰參數K的取值對準確率的影響。結果如圖4、圖5所示。從圖中可以看出，近鄰參數K的取值只有在一定范圍時，聚類效果才能達到最好。一般為3～8。

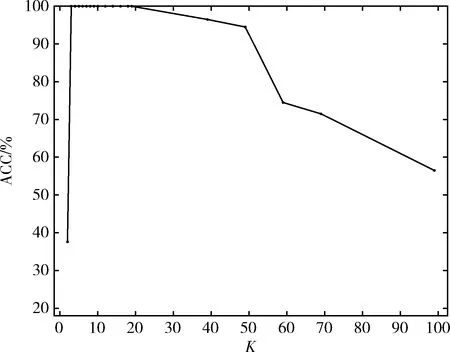
圖4 CSCA算法下近鄰參數K對雙月數據聚類結果的影響

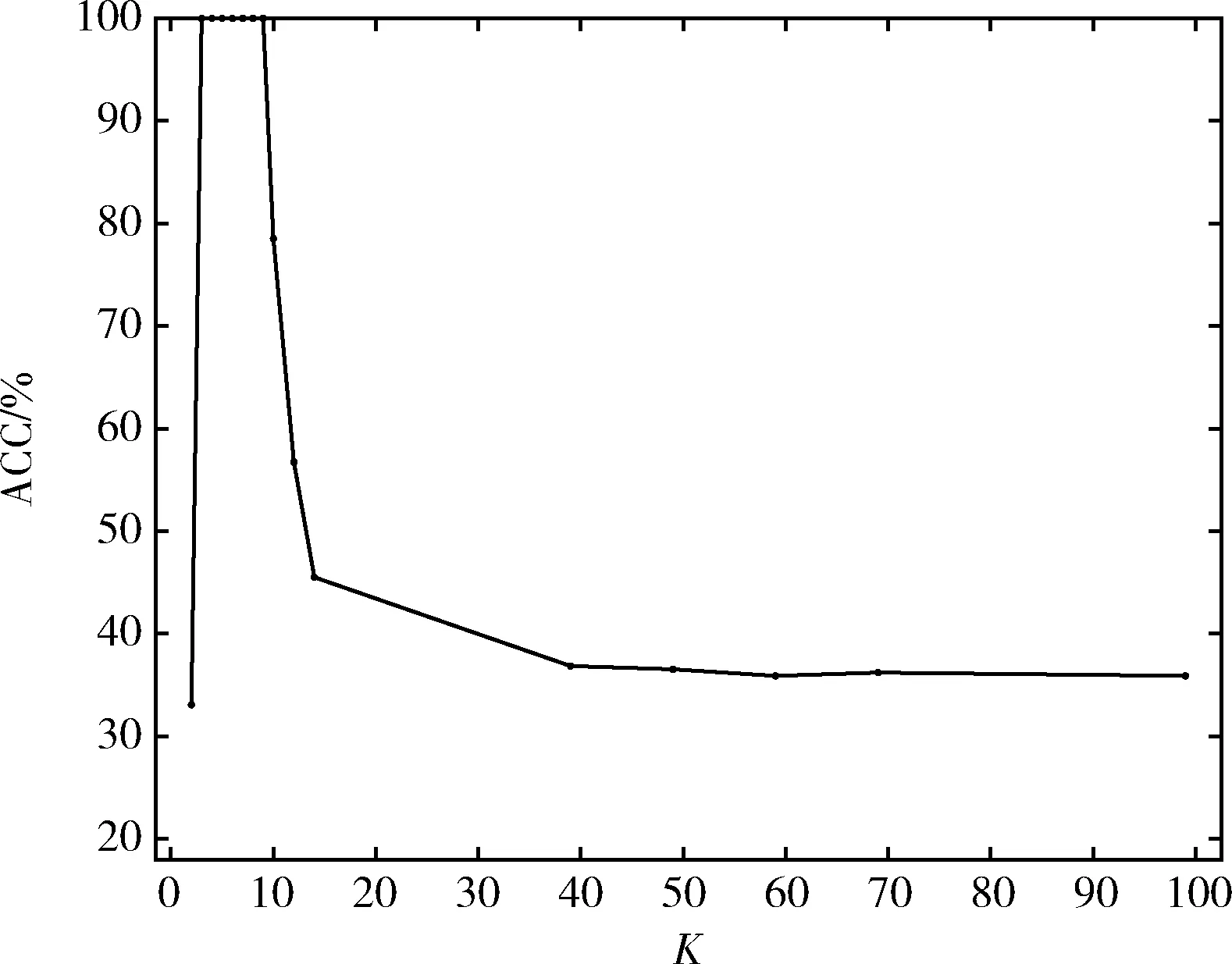
圖5 CSCA算法下近鄰參數K對Spiral 數據聚類結果的影響

2.2 人臉數據庫(ORL)聚類

ORL包含40個不同人的面部圖片，每一個都有10張不同的圖片。這些照片是在不同的時間拍攝的，并改變了光線、面部表情和面部細節。所有的圖片都是在暗色均勻的背景下拍攝的，支架處于直立、正面的位置(可以容忍一些側面的運動)。每個圖片的分辨率大小為92×112。

實驗使用了ORL人臉數據庫中的前20個人的人臉圖片，共200張圖片，并把每張圖片轉換為10 304維的數據進行實驗。實驗結果如圖6所示，并給出CLR_W的結果，如圖7所示，可以發現CSCA的實驗結果明顯優于CLR_W。

圖6 CSCA對人臉數據集的聚類結果(ACC=88.50%)

圖7 CLR_W對人臉數據集的聚類結果(ACC=77.00%)

2.3 真實數據集

在針對真實數據集的實驗中，采用了6個真實數據集Yeast、Abalone、MSRA25、USPSdata20(http://www.pudn.com /Download/item/id/3945155.html)、Iris、Lung上進行實驗，前兩個是UCI機器學習庫中的生物信息學數據集。它們含蓋了高維與低維、多樣本與少樣本以及多類別與少類別等各種真實數據集的特點。6個真實數據集的參數見表1。

在真實數據集上的實驗結果見表2、表3，其中加粗的數據表示結果最好，加下劃線的次之。表2顯示的是各數據集下不同算法的ACC對比；表3顯示的是各數據集下不同算法的NMI對比。在真實數據集的實驗結果上顯示，對于不同的真實數據集，聚類算法CSCA在大多數情況下是優于其它算法的。所以，這也驗證了聚類算法CSCA的有效性。

表1 真實數據集信息

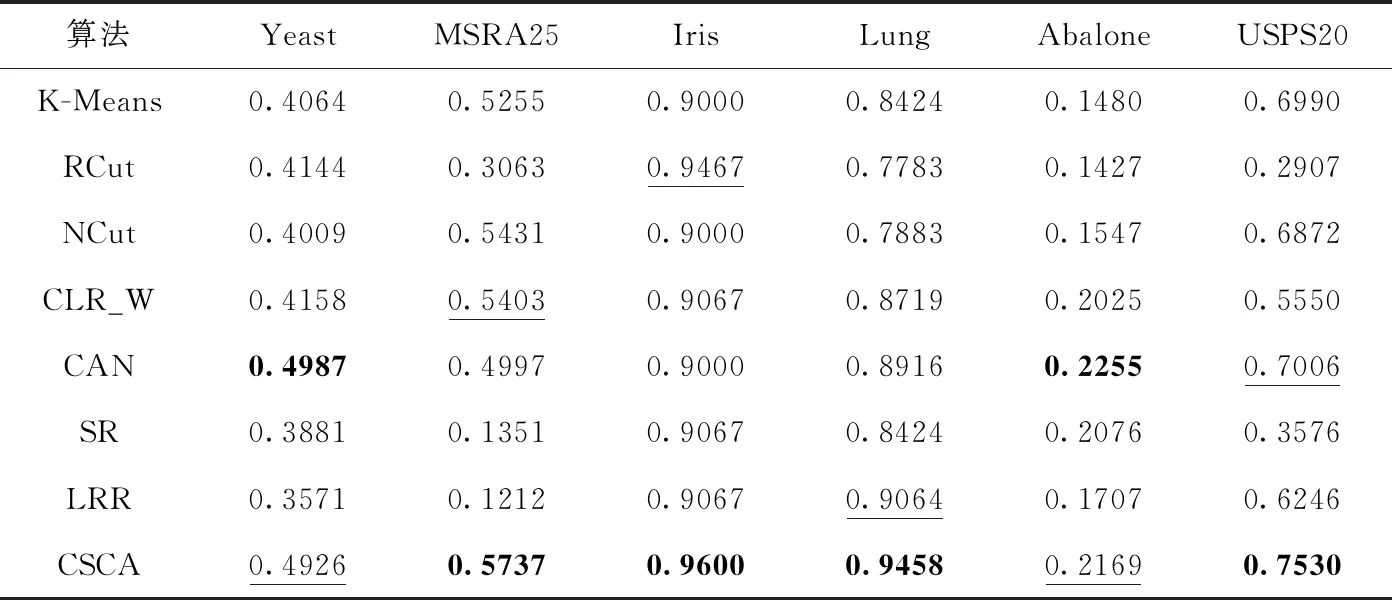
表2 各數據集下不同算法的ACC對比

表3 各數據集下不同算法的NMI對比

3 結束語

CSCA算法是L2,1-范數距離來學習相似度矩陣的，從而增加聚類算法的魯棒性，引導相似度矩陣的稀疏性；并用平方約束相似度矩陣；通過對相似度矩陣的拉普拉斯矩陣施加秩的約束，來實現聚類的。也可以利用K-Means對F進行聚類，得到聚類結果。該算法與對比算法相比，在大多數情況下，結果是優于對比算法的，該算法在多個數據集上的實驗結果也能說明這一點。但是由于近鄰參數K值的選取，是人為選取的，且對含有噪聲的數據集的聚類結果影響較大。從而使得該算法具有一定的局限性，所以接下來本文將對于如何消減噪聲的影響做進一步的改進。一方面，可以用其它消減噪聲的影響的方法來代替K近鄰，或者進一步的改進近鄰參數K值的選取方法，使其在實驗不同的數據集時使其能夠自動調整；另一方面，可以選取合適的正則項，對相似度矩陣施加正則化，或者引入合適的半監督學習方法，來學得更好的相似度矩陣。