基于馬爾可夫跳變神經網絡的采樣同步控制研究

田佳萍，謝立典，王春柱，王嘉偉，葛超

（1.華北理工大學人工智能學院，唐山063210；2.石家莊海山實業發展總公司，石家莊050200；

3.火箭軍綜合訓練基地學兵訓練一隊，唐山064000）

研究馬爾可夫模型的神經網絡采樣控制的主從同步問題。在零輸入策略的框架下，提出一種新型的可變采樣隨機切換采樣數據控制器。基于Lyapunov函數方法，構造適當的Lyapunov-Krasovskii函數（LKF）充分利用有關實際采樣模式的可用信息。使用凸組合技術和自由權矩陣的積分不等式，得出一些充分條件。通過求解線性矩陣不等式（LMI），可獲得相應的采樣數據控制器。給出的數值算例說明該方法的有效性和優勢。

采樣控制；馬爾可夫跳變；LMI；神經網絡

0 引言

如今，由于神經網絡已廣泛用于各個領域，例如信號處理、圖像處理、模式識別、優化和關聯存儲設計等，因此，神經網絡受到了廣泛的關注[1-2]。對于控制界來說，神經網絡的吸引力在于它們可以完全近似復雜的非線性映射關系，并且它們可以學習并適應不確定系統的動態特性。以這種形式，將神經網絡引入控制系統是控制學科發展的必然趨勢。近年來，與神經網絡有關的穩定性分析已被深入研究，并獲得了很多成就[3-4]。

隨著對神經網絡問題的研究，神經網絡同步控制問題逐漸被發現和廣泛研究。神經網絡的同步控制處于神經網絡的穩定性之下。為了保持主從系統的同步狀態，設計了合適的控制器。神經網絡的主從同步已逐漸成為必不可少的研究領域。近年來，已經提到了許多重要的主從同步方法，例如脈沖控制[5]、固定控制[6]、輸出反饋控制[7]、自適應控制[8]和采樣數據控制[9]。

得益于計算機技術的進步和對其的深入研究，在過去的幾十年中，采樣數據控制系統引起了越來越多的興趣。一些文獻[10-11]報告了許多基本結果。為了同步，被采樣的數據僅需要關于采樣時刻的系統狀態的信息，其方法的特點是減少了傳輸的信息并提高了控制效率。使用采樣數據控制實現神經網絡同步時，選擇采樣周期是一個重要的問題。更長的采樣間隔將帶來更低的通信信道占用，更少的信號傳輸以及更少的驅動控制器信號[12-13]。采用了一種新的LKF和線性矩陣不等式（LMI）技術來研究動態網絡采樣數據的同步控制。因此，設計具有更長采樣周期的同步控制器尤為重要。

在另一個研究前沿，眾所周知，馬爾可夫跳躍系統是一種有限模式操作的特殊動力學系統，由于其在許多動力學模型中的潛在應用，在過去的幾十年中一直引起越來越多的研究關注[14]。在文獻[15]中研究了具有輸入振幅約束的不確定Markovian跳躍神經網絡的有限時間同步控制。文獻[16]研究了具有時變間隔和時滯的Markovian跳躍廣義神經網絡的耗散穩定性分析問題。總結已有文獻，對采樣數據神經網絡系統的馬爾可夫跳躍研究具有重要意義。

1 模型建立和問題描述

1.1 基于丟包的神經網絡采樣的同步控制系統的模型構建

我們構建的神經網絡模型如下：

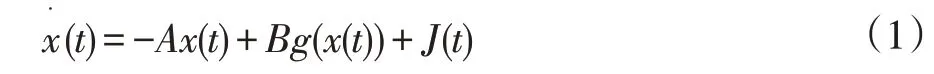
其 中 x(t)=[x1(t)，x2(t)，…，xn(t)]T表 示 狀 態 向 量。A=diag{a1，a2，…，an}表示的正定對角矩陣，其中Ai＞0；B=(bij)n×n表示連續的權重矩陣；J(t)=[J1(t)，…，Jn(t)]T為常數的輸入向量；g(x(t))=[g1(x1(t))，g2(x2(t))，…，gn(xn(t))]T表示神經元的激活函數。

假設g(?):Rnh→Rnh是屬于扇區[σ-i，σ+i]，i=1，2，…，nh的非線性函數。也就是說，非線性函數g(?)滿足以下條件[29]：

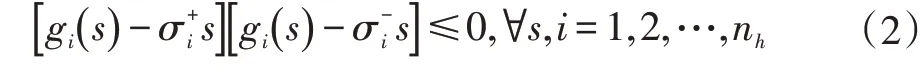
在完全概率空間中，我們設{r(t)，t≥0}是一個右連續Markov鏈。它描述了t時間模式的演化，取有限狀 態 空 間G={1，2，…，N}中 的 值，其 生 成 元γ=(γij)，( i ，j∈G)由下式給出：

結合上述，具有馬爾可夫跳變的神經網絡主系統被表示為：

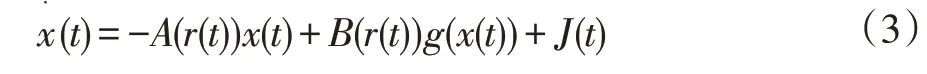
對應的從系統表示為下列形式：

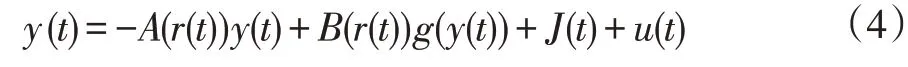
其中，u(t)=Ke(tk)表示基于采樣時刻tk的控制輸出，K為待求解采樣數據控制器的增益矩陣。

結合上述主從系統，令e(t)=y(t)-x(t)，可以得到如下的誤差系統：

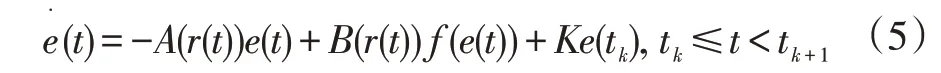
當s∈R且s≠0時，函數fi(s)滿足以下條件：

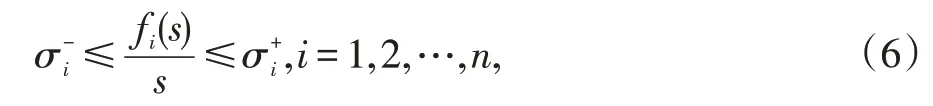
1.2 相關定義和引理

2 定理

在這部分，我們將找到一種方法求解控制器矩陣K。為了簡化矩陣表達式，我們給出以下定義：

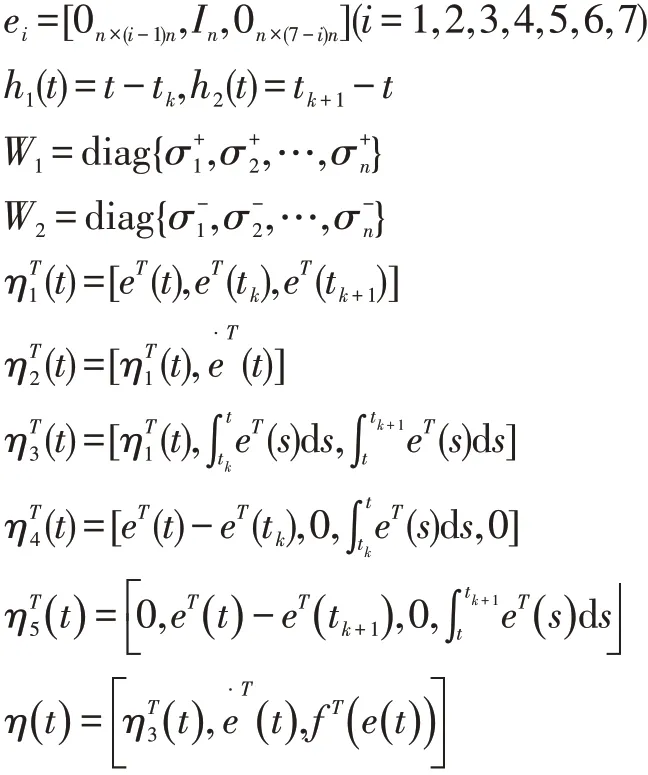
對于給出的參數值h＞0，?1＞0，?2＞0，誤差系統

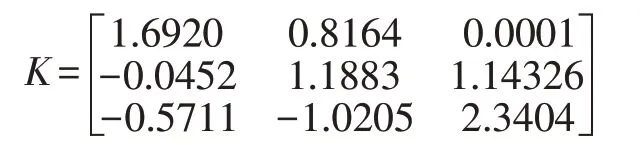
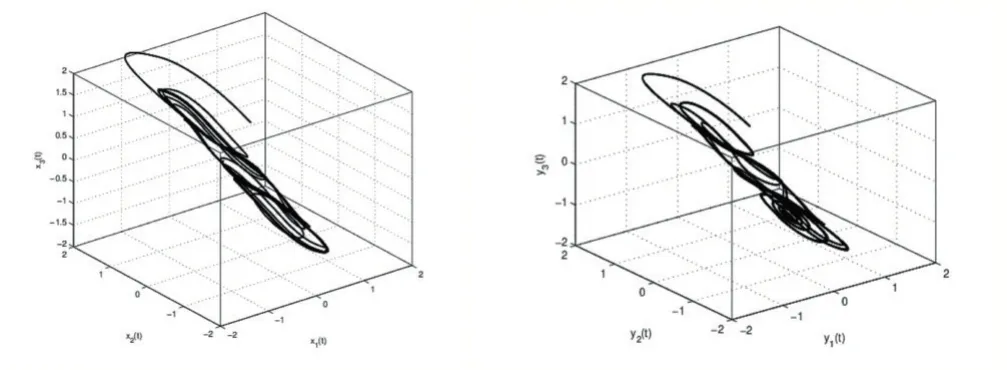
圖1 神經網絡主從系統的狀態反應

利用得到的上述增益K，控制器u(t)的對應關系如圖2所示，誤差狀態e(t)如圖3所示。由圖3可知，狀態變量的變化趨勢最終趨近于0，這也驗證了我們方法的有效性和可行性。

圖2輸出控制曲線u（t）

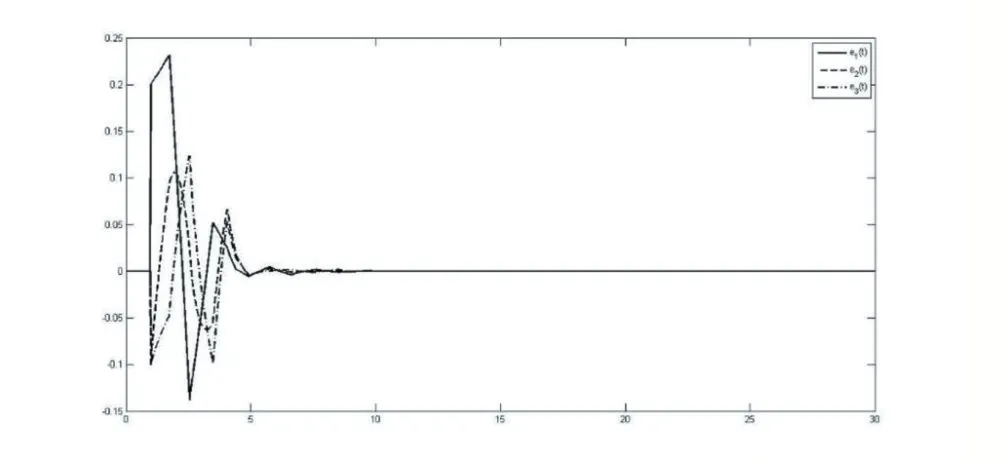
圖3 含有控制輸入的誤差系統的狀態響應

4 結語

在本文中，我們提出了一種新的馬爾可夫跳躍神經網絡的隨機切換采樣數據控制方案。通過零輸入法的框架，伯努利分布模型已用于建模。與相關文獻相比，馬爾可夫過程更為通用和實用。為了充分利用各種可用信息，構造了一個新的增強LKF來分析相應的錯誤系統。基于Wirtinger不等式，獲得了一些較不保守的條件來保證主從系統的同步。此外，可以通過求解LMI來合成采樣數據控制器增益矩陣，該矩陣取決于最大允許的采樣周期。最后，一個數值算例表明了該方法的有效性和優點。