深部巷道直墻半圓拱形鋼管混凝土支架承載性能分析①

陳 斌， 左宇軍，2，3， 王 劍， 孫文吉斌， 鄭祿璟， 林健云

(1.貴州大學 礦業學院,貴州 貴陽550025； 2.喀斯特地區優勢礦產資源高效利用國家地方聯合工程實驗室,貴州 貴陽550025； 3.貴州省非金屬礦產資源綜合利用重點實驗室,貴州 貴陽550025； 4.中南大學 資源與安全工程學院,湖南 長沙410083)

近年來,德國、加拿大、澳大利亞、中國以及南非等國家的許多金屬礦和煤礦開采深度已超千余米,有的金屬礦山開采深度甚至超三千米,資源開采轉向深部開采［1-2］。 在轉入深部開采后,受“三高一擾動”等復雜條件作用,巷道圍巖處于與淺部開采不同的非線性地質力學環境中,其中以高地應力影響最為顯著［3］。受高地應力、(極)軟巖等復雜地質條件影響,出現了大量深部難支護巷道。 承載能力較低的一般金屬支架不能有效控制深部高應力巷道的變形［4-5］。 我國常用的深部高應力軟巖巷道支護方式為U 型鋼支架＋錨網噴聯合支護,已取得較好的支護效果和大量的研究成果,但在轉向更深的開采條件時也表現出承載強度不足、U 型鋼自身結構缺陷、截面受力不合理等缺點［1］。

為解決深部高應力軟巖巷道的難支護問題,持續有人嘗試新觀念、新工藝以及新材料,最具代表性的當屬采用鋼管混凝土支架。 該結構的工作狀態是:外部鋼管與內部混凝土相互共同作用,形成“力的共生”現象［6-7］,使鋼管混凝土支架具有較高的承載力。 在巷道支護中,直墻半圓拱形斷面是最常用的斷面形狀,具有諸多優點,但目前鋼管混凝土支架的設計應用多集中在圓形和橢圓形斷面［8］,而對直墻半圓拱形斷面結構研究較少。

為了推動直墻半圓拱形鋼管混凝土支架在深部高應力巷道中的應用,本文在現有鋼管混凝土支架的研究基礎上,對鋼管混凝土支架的承載力進行計算和分析,進一步通過ANSYS 軟件建立三維耦合模型,得到不同側應力系數下支架的變形情況,綜合研究兩類支架的支護效果,為解決深部高應力軟巖巷道支護難題提供技術依據。

1 工程概況

貴州某礦區270 中段巷道斷層、節理裂隙發育,部分節理已呈張開狀態,圍巖整體較破碎,穩定性較差。在270、290 中段進行取坑內鉆取芯工作,采用RQD(巖石質量指標分類)進行巖體質量評價,由于礦山使用坑內鉆探礦,巖芯為圈定礦體的探礦巖芯,分為礦體下盤、礦體和礦體上盤3 部分,鉆孔巖芯RQD 值分別為29.37%、30.23%和41.92%,所以巖體整體破碎,穩定性不好,根據巖石RQD 分類標準,巖石質量呈“差”等級。 結合現場調查的圍巖裂隙程度和巖石質量指標評價,最后將巷道圍巖定義為穩定性較差的Ⅳ級巖體［9］。

2 支架承載力理論計算

2.1 U 型鋼支架承載力計算

通過文獻［10］可知,隨著測應力系數逐步增大,U型鋼支架支撐力逐漸減小。 而深部巷道的典型特征是水平應力高于垂直應力,某些深部巷道的側應力系數甚至超過1.5。 因此,在深部高水平應力巷道中采用U型鋼支架支護無法達到需要的支護效果。

2.2 鋼管混凝土支架承載力計算

鋼管混凝土支架選取Φ194 mm × 8 mm 的20＃無縫鋼管灌注C40 核心混凝土,其斷面形狀和大小與U型鋼支架保持一致。

2.2.1 鋼管混凝土短柱承載力計算

鋼管混凝土短柱的軸壓承載力Nx計算公式為［6］:

式中Nx為鋼管混凝土短柱的承載力；Ac為核心混凝土的橫截面積；fc為核心混凝土抗壓強度,fc＝26.8 MPa。 套箍指標θ 表示外部鋼管對核心混凝土套箍約束程度,,其中As為鋼管的橫截面積,fs為鋼管的屈服強度,鋼管和混凝土核心的參數見表1 ～2。 計算可得:Nx＝2 798.72 kN。

表1 鋼管參數

表2 混凝土參數

2.2.2 鋼管混凝土支架承載力計算

壓彎組合是鋼管混凝土支架在實際承載過程中的受力狀態,考慮長細比和偏心率的綜合作用,支架的承載能力為:

式中N0為支架的極限承載能力；φ 為極限承載能力的折減系數,受長細比以及偏心率的綜合影響,取φ ＝0.78［5］。計算得:N0＝2 183 kN。

通過對比可知,理論計算得出的鋼管混凝土支架的承載力遠大于U 型鋼支架。 從理論計算結果來看,在高應力巷道中采用鋼管混凝土支架支護是更優選擇。

3 數值試驗分析

3.1 力學模型建立與邊界約束

數值計算模型以某礦區270 中段實際工程地質條件為背景,依據巖體力學相關理論,一般取巷道寬度的3～5 倍作為巷道開挖后的應力調整范圍［11］,聯系巷道工程實際尺寸,采用ANSYS 有限元軟件建立圍巖與支架耦合模型,巷道圍巖模型尺寸為32 m ×32 m ×3 m,整個模型分為兩部分:圍巖體和支架。 固定約束整個數值計算模型的底部,限制前后面的法向位移,模型頂部和側面逐步施加壓力。 根據深部礦山圍巖裂隙程度,將圍巖質量劃分為5 個等級,選取的參數與不穩定的Ⅳ級巖體相似［9］,結合270 中段實際地質情況和相關資料［12］,U36 型鋼以及圍巖參數如表3～4 所示。 在整個數值模擬過程中,由于不能將所有影響巷道穩定性的因素都考慮進去,因此對所做模擬進行以下必要假定:①將圍巖體視為連續均質、各向同性的力學介質；②在計算的過程中圍巖體不產生滑移；③假定支架與圍巖體之間完全接觸。

表3 U36 型鋼參數

表4 圍巖參數

3.2 數值試驗結果及分析

不同側應力系數條件下進行數值試驗,在鋼管混凝土支架上選取32 個監測點,U 型鋼支架上選取24個監測點,如圖1 所示。

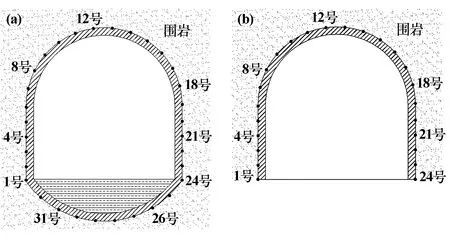
圖1 監測點模型

在深部巷道中水平應力對巷道圍巖體穩定性的影響比垂直應力更為顯著。 在支架間距1.0 m、側應力系數分別為1.0、1.5、2.0 條件下進行模擬,得到鋼管混凝土支架和U 型鋼支架的變形情況如圖2 ～3 所示。 由圖2～3 可知,隨著側應力系數增大,支架的最大變形量也隨之增大。 主要受力為虛線部分。

圖2 不同側應力系數下鋼管混凝土支架變形云圖

圖3 不同側應力系數下U 型鋼支架變形云圖

提取鋼管混凝土支架和U 型鋼支架監測點在不同側應力系數下的變形量,繪制曲線,如圖4 ～5 所示。圖4 中當側應力系數為1.0 時,鋼管混凝土支架底角與頂拱的變形量相差較大,反底拱的變形量較小且往底拱中心方向變形量逐漸減小,但整體變化不大。 說明此時頂底拱受力較小,而底角的受力較大。 隨著側應力系數逐漸增大,頂底拱的變形量也隨之增加；底角的變形量增幅較小,變形量均在6～7 mm 之間；反底拱中心處的變形量大于兩端。 從7 ～18 號監測點可看出,側應力系數為2.0 時頂拱的拱形最為凸顯,此時頂拱受力超過底角,變為整個支架受力最大的部分。 反底拱中心處的受力逐步增大,最后大于兩端受力。 支架底角應力變化不大,但應力較高,主要原因是底角部位容易產生應力集中。 應對其底角部位進行監測觀察,防止其首先變形破壞,從而影響支架的整體承載能力。 側應力系數逐漸增大,但鋼管混凝土支架底角變形量增幅較小,表明其在深部高水平應力巷道中有良好的適用性。

圖4 不同側應力系數下鋼管混凝土支架變形折線圖

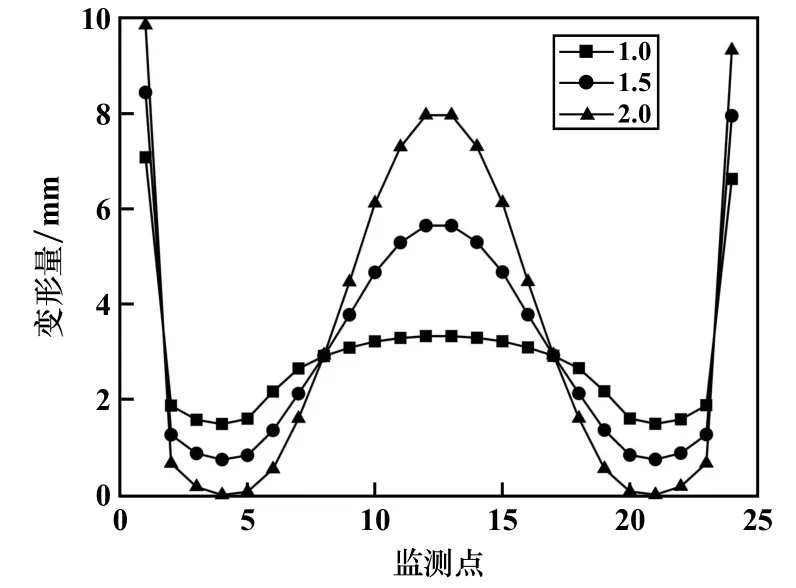
圖5 不同側應力系數下U 型鋼支架變形折線圖

圖5中當側應力系數為1.0 時,U 型鋼支架頂拱變形量較小且遠小于底角的變形量,此時與頂拱相比底角的受力較大。 側應力系數逐步增大時,支架頂拱和底角的變形量隨之增加,從7 ～18 號監測點可看出,側應力系數為2.0 時頂拱的拱形最凸顯。 其中,在同一側應力系數時,底角的變形量始終大于頂拱,且為支架整體的最大值。 表明底角所受應力是整個支架受力的最大部位。 因此,U 型鋼支架的腿部會最先遭到變形破壞,從而影響支架的整體承載能力,這也是U 型鋼支架不適用于深部高水平應力巷道的原因。

在相同側應力系數下提取鋼管混凝土支架的前24 個監測點和U 型鋼支架的全部監測點,繪制曲線,如圖6 所示。 當側應力系數為1.0 時,除1 號監測點U型鋼支架變形量差值稍大外,兩類支架在各監測點的變形量基本相等。 隨著側應力系數增加,鋼管混凝土支架底角的變形量變化較小；而U 型鋼支架底角的變形量急劇增加,遠大于鋼管混凝土支架底角的變形量,兩類支架其他監測點變形量基本保持相同。 其中,當側應力系數為2.0 時,鋼管混凝土支架頂拱的變形量大于底角,而U 型鋼支架頂拱的變形量始終小于底角。 進一步表明,與鋼管混凝土支架相比,U 型鋼支架腿部是其最薄弱的部位,在深部高水平應力巷道中使用時會首先遭到破壞,不適合在水平應力較高的巷道中采用。

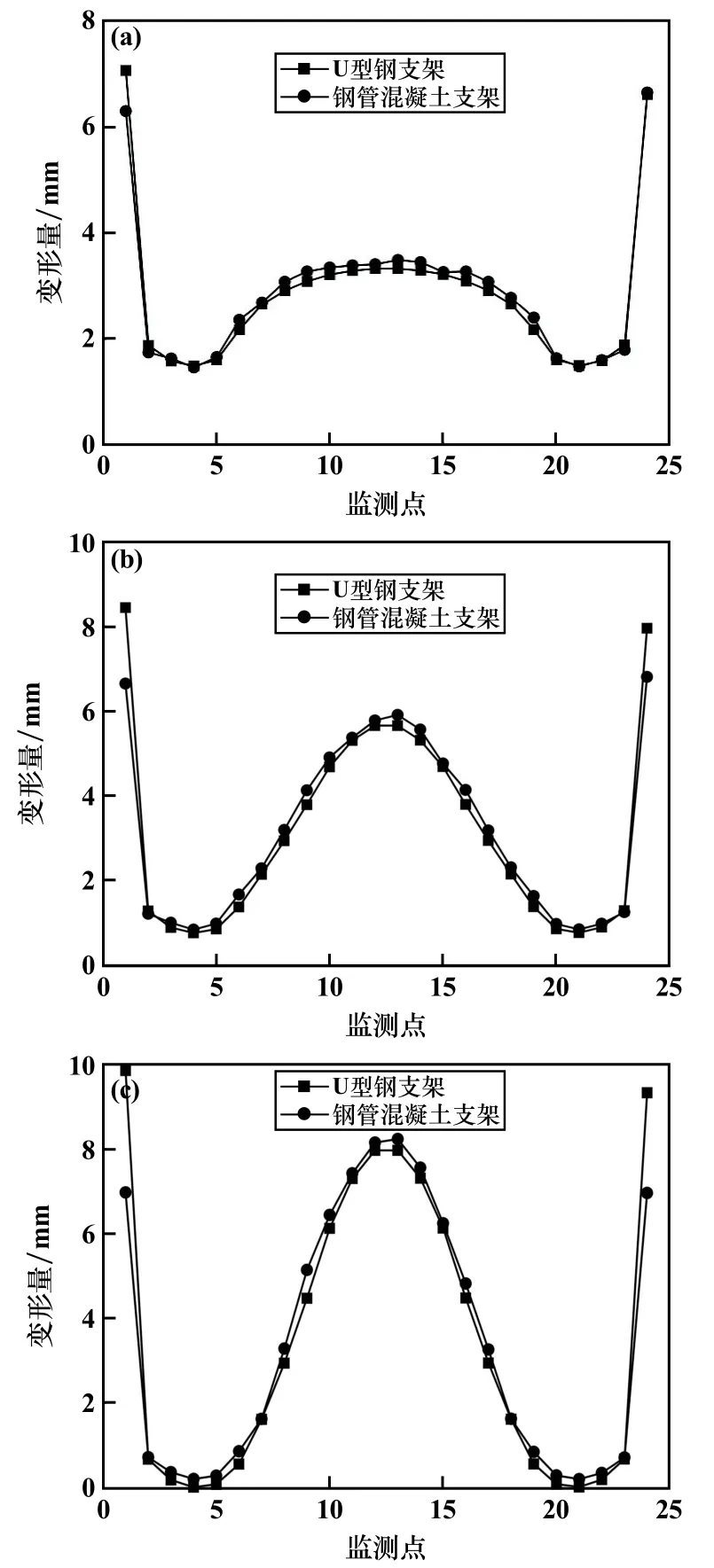
圖6 相同側應力系數下兩類支架變形折線圖

4 結 論

1) 理論分析結果表明,鋼管混凝土支架的承載力遠大于U 型鋼支架。 受U 型鋼支架自身結構影響,隨著側應力系數增加,U 型鋼支架的承載力呈降低趨勢。

2) 數值模擬結果表明,當側應力系數為2.0 時支架變形量達到最大,鋼管混凝土支架和U 型鋼支架的最大變形量分別為9.136 4 mm 和13.046 0 mm,最大變形量位置分別在頂拱和底角處；隨著側應力系數增大,鋼管混凝土支架底角變形量增幅較小且低于U 型鋼支架,U 型鋼支架腿部最先遭到破壞,而鋼管混凝土支架整體承載性能良好。

3) 相比于U 型鋼支架,直墻半圓拱形鋼管混凝土支架承載性能優越,在解決深部高水平應力巷道圍巖穩定性問題中有良好的潛力。