直角切削6061-T6鋁合金剪切區力學行為及微觀結構演化預測

周滔,何林,2,*,田鵬飛,杜飛龍,3,吳錦行

1. 貴州大學 機械工程學院,貴陽 550025 2. 六盤水師范學院 礦業與土木工程學院,六盤水 553000 3. 貴州大學 現代制造技術教育部重點實驗室,貴陽 550025

機械加工屬于典型的基于熱力耦合的塑性變形過程,并伴隨材料的微觀結構演變。過去幾十年發展起來的基于物理的解析方法為理解機械加工過程奠定了堅實的基礎,但是早期的解析性模型(如Merchant[1]、Hill[2]和Lee[3])在模擬切削過程中的切屑變形涉及的力學行為時,大多沒有考慮金屬材料的微觀結構性能,而切削過程中金屬材料的力學行為與微觀結構緊密相連。近年來,大量包含微觀結構的材料模型[4-5]被成功開發和應用,甚至擴展到高應變、應變率和高溫變形過程[6-7],所以當前研究切削過程中微觀結構演化并將其嵌入到預測加工理論模型已經成為可行。

為了將微觀變形與宏觀力學行為聯系起來,很多研究人員做了相關的建模工作。如Pan等[5]提出在Johnson-Cook(JC)方程中考慮晶粒長大的影響,并將其代入Oxley模型中迭代計算切削力,模型提高了預測精度。金屬材料在高溫塑性變形時,變形機制主要表現為擴散,當切削溫度相對于熔點較低時,變形機制主要有位錯和孿生。為了更好地描述切削加工這類冷加工大變形條件下的材料行為,有很多基于金屬位錯機制的材料模型(Dislocation Density-based Material model, DDM)被開發利用,Bammann等[8]考慮應變率、溫度和損傷建立了一個基于位錯密度的材料模型。Guo等[9]預測切屑形貌時,發現與JC模型相比,Bammann-Chiesa-Johnson (BCJ)模型更為準確。Follansbee和Kocks[10]建立了一個基于熱無關應力和熱應力的粘塑性模型,且考慮了初始晶粒尺寸的影響。Ding和Shin[11]基于位錯的增殖和湮滅過程有效地預測了切削AISI 52100 steel的切削力、切削溫度和切屑厚度。Liu等[4]驗證了考慮位錯拖拽的統一材料模型在大范圍內的切削力預測準確性。這些基于物理的材料模型在預測性能上的改進使得它們比非物理動機的唯象學模型更有吸引力。

建立微觀結構演化過程與切削條件之間的關系是金屬加工過程建模的另一個挑戰。6061-T6鋁合金具有中等強度、良好的抗腐蝕性、可焊接性,氧化效果較好,廣泛應用于要求有一定強度和抗腐蝕性高的工業結構件[12],例如航天固定裝置、電器固定裝置及自動化機械零件等。Ding等[7]采用Estrin等[13]開發的基于位錯密度的材料模型模擬了6061-T6鋁合金切屑在直角切削過程中的晶粒細化。Arisoy和?zel[14]結合平均晶粒的計算方法提出了車削Ti-6Al-4V時的晶粒尺寸演化有限元模型,結果表明,再結晶晶粒對材料在主剪切區的力學行為有顯著影響,從而導致了切屑的分段,這甚至可以用于揭示鈦合金鋸齒狀切屑[15]的形成機理。Jafarian等[16]使用再結晶機制模擬了直角切削Inconel718的微觀結構變化,其中考慮晶粒尺寸的流動應力模型正確反映了材料力學行為。以上研究中,在考慮微觀結構演化對材料的力學行為影響時,大多是基于有限元法(Finite Element Method, FEM)實現。相對于FEM的微觀結構演化預測,解析模型為加工過程建模提供了一種簡便的方法,具有較高的計算效率,可以顯式地計算加工過程中材料的熱力耦合響應。

綜上所述,本研究的目的是結合金屬材料微觀結構中位錯變形機制和預測加工理論,建立一種能描述主剪切區(Primary Shear Zone, PSZ)力學行為和模擬微觀結構演化過程特征的解析模型。首先將位錯密度材料模型與等分模型和非等分模型結合,構建了剪切區應力場和溫度場分布的計算流程,提出了切屑微觀結構(位錯密度和晶粒尺寸)演化解析模型,然后使用透射電子顯微鏡結合選區電子衍射對直角切削6061-T6鋁合金的切屑塑性變形狀態進行觀測,對等分模型和非等分模型的切削力預測結果進行了驗證,通過混合等分模型和非等分模型給出的應變場和溫度場,預測了剪切區微觀結構演化過程,實驗結果證明了所建立模型的可行性。

1 位錯密度材料模型

切削剪切區的大塑形應變累積導致的位錯運動會使切屑材料發生晶粒細化,如圖1 所示,本文在描述剪切區力學行為時,為了模擬切屑形成過程中的晶粒細化過程,采用基于位錯密度的材料模型。

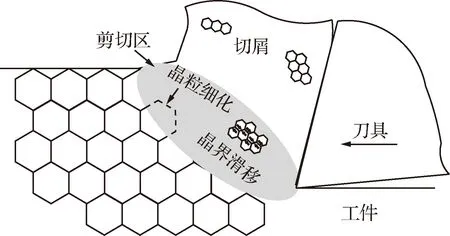
圖1 剪切區晶粒細化Fig.1 Grain refinement of shear zone

為了反映切削過程中剪切區力學行為,建立切屑內位錯密度和晶粒尺寸的演化模型,引入由Estrin等[13]建立的位錯密度材料模型,該模型由胞壁和胞內兩部分組成,在塑性變形過程中形成位錯胞結構,分為胞內位錯ρc和胞壁位錯ρw,其中胞壁位錯又由統計位錯ρws和幾何必需位錯ρwg組成,每一種位錯的演化遵循不同的計算方法,ρc、ρws和ρwg的微分方程為

(1)

(2)

(3)

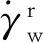
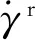
(4)

(5)

通過位錯胞壁體積分數、位錯密度和晶粒尺寸之間的關系,可以得到表達式分別為

(6)

ρtot=f(ρws+ρwg)+(1-f)ρc

(7)

(8)

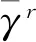
在建立的解析模型中,通過考慮位錯密度來計算金屬材料的流動應力,以此確定力學性能,通過Taylor因子M進一步定義了流動應力σ和分解剪應力τr的關系

τr=σ/M

(9)

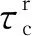
(10)

(11)

式中：G為剪切模量；1/m為應變速率敏感參數；a為常數在0.25到0.5之間。“混合”材料的整體性能由τr來定義,其根據式(12)的兩“相”混合規則得到

(12)

其中,n和m與溫度有關,m=A/T,n=B/T,A和B為常數,T為溫度。

2 基于熱力耦合的切削力預測

在預測切削力時,解析模型和有限元數值方法得到了廣泛的應用,雖然有限元具有高精度和多功能等優點,但是需要花費更多的時間來模擬。Oxley預測加工理論基于對材料變形的實驗觀察,在平面應變和穩態切削條件的假設下可以實現計算效率高且精確的預測,同時建立起直角切削輸入變量(材料特性、刀具幾何形狀和切削條件)與輸出變量(變形區的溫度、切屑幾何形狀、切削力等)之間的理論關系。

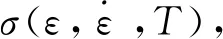
通過圖2所示剪切區和刀具-切屑接觸區的平衡關系可以求解出各切削力分量和切屑厚度t2,如式(13)～式(18)所示:

Fc=FRcos(λ-α)

(13)

Ft=FRsin(λ-α)

(14)

Ff=FRsinλ

(15)

Fn=FRcosλ

(16)

(17)

t2=t1cos(φ-α)/sinφ

(18)

式中：φ為剪切角；α為刀具前角；λ為摩擦角；t1為未變形切屑厚度；w為切削寬度；Fc和Ft為切屑形成力在切削方向和垂直于切削方向上的分量；Ff為刀具-切屑界面的摩擦力；Fs為剪切面上的切削力；FN和Fn分別為剪切面和刀具-切屑界面的法向力；FR為Ff和Fn的合力；Fc和Ft的合力為-FR；θ為FR與AB的夾角；KAB表示剪切面平均流動應力。已知剪切面上的剪切應力和刀具-切屑界面的摩擦角,在給定刀具幾何形狀和切削條件下,可以預測直角切削過程中的切削力。

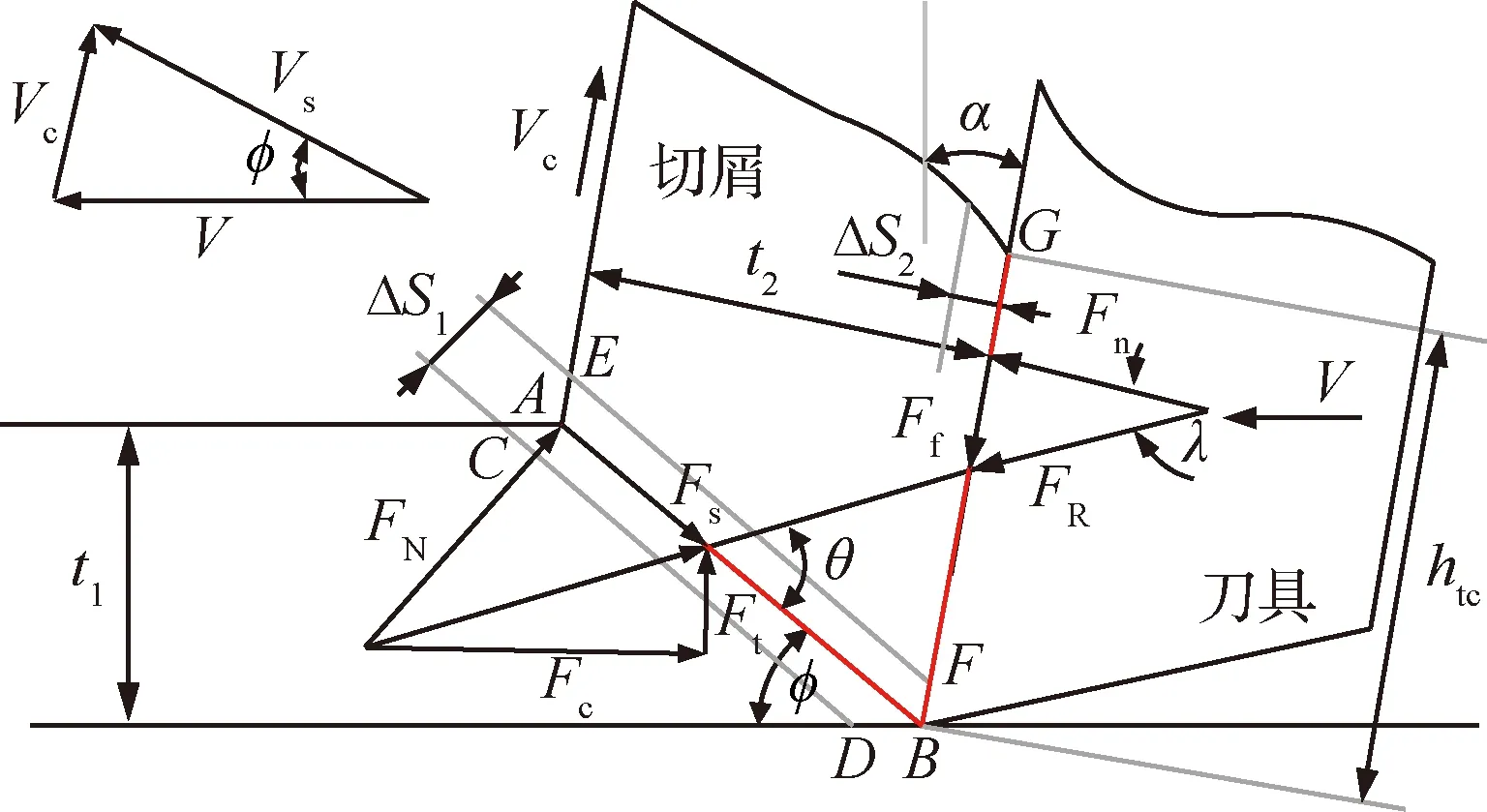
圖2 直角切削幾何關系Fig.2 Geometric relations of orthogonal cutting

假設從A到B的任意質點在切削方向x和垂直于切削方向y上的速度和位移增量分別為

(19)

(20)

式中：V為切削速度；ΔS1為第一變形區厚度。

Oxley模型[18]中剪切區材料流動速度分量和平均剪應變速率之間的關系為

(21)

將式(19)和式(20) 代入式(21),可得平均剪應變速率表達式

(22)

剪切角φ確定后,根據von Mises應力屈服準則,剪切區的AB處等效應變和等效應變率為

(23)

(24)

假設所有的變形都發生在剪切平面上,在剪切平面上工件材料變成了切屑,初始切削速度為V的工件材料,隨著切削速度的增加,會突然向切屑轉變,速度的這種突然變化沿剪切面產生了速度不連續,即所謂的剪切速度,通過圖2的速度矢量關系圖可以計算切屑材料流動速度Vc和剪切面的材料流動速度Vs:

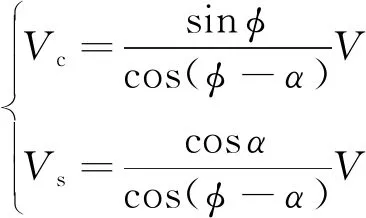
(25)

切削時的摩擦角計算公式為λ=θ+α-φ,可以得到摩擦系數μ=tanλ,根據Oxely理論,圖2中的剪切角φ和夾角θ滿足以下關系：

(26)

修正的應變率常數C0考慮了材料應變的影響[19],其表達式為

(27)

式中：COxley為第一變形區剪切帶長寬比；AJC、BJC和nJC為JC本構參數。

由于剪切應力與溫度有關,因此需要迭代計算AB的溫度,直到達到穩態。根據Boothroyd溫度模型[20],平均溫度的表達式為

(28)

式中：Tr為室溫,η為總剪切能轉換為焓的比例,分析中取0.9[20]；ρ為工件材料的密度；Cw為工件材料的比熱。其中熱量分配系數β計算[21]如下

β=

(29)

(30)

式中：Kw為熱傳導系數；R0為無量綱熱系數。

圖2中靠近刀尖位置處的B點的正應力σ′N可結合剪切面的平均流動應力得到

(31)

分析第二變形區時,通常假設刀具-切屑界面的塑性變形區域的厚度為常數：ΔS2=δt2,δ為第二變形區厚度與切屑厚度之比。因此,得到刀具-切屑界面的等效應變和等效應變率為

(32)

(33)

式中：刀具-切屑接觸長度htc根據剪切面的力矩平衡公式求出

(34)

假設刀具-切屑界面應力均勻分布,得到刀具-切屑界面應力τint和B點的應力σN表達式為

(35)

刀具-切屑界面的平均溫度Tint表示為

Tint=Tr+ΔTsz+ψΔTM

(36)

(37)

(38)

式中：Ψ為修正系數,取為0.6[20]；ΔTM為切屑中的最大溫升；ΔTc為切屑中的平均溫升；ΔTsz為第一變形區溫升。

基于熱力耦合的切削力預測模型中,求解剪切區溫度時,先在給定的初始溫度下,確定剪切區的流動應力,然后根據流動應力使用式(28)更新剪切面的溫度,并替換為初始啟動溫度,開始新的計算,這個過程不斷重復,直到起始溫度和計算溫度之間的差值小于給定值0.1 ℃,根據三個迭代條件[21](刀具-切屑界面處的應力平衡、刀尖處的應力平衡和切削力Fc最小原則)確定剪切角φ和變形區應變率系數COxley和δ,輸出切削力。

由于切削過程中的變形具有典型的高應變、高應變速率和高溫的特點,在之前修正的Oxley模型中,剪切區和切屑中相應的平均流動應力采用Johnson-Cook本構方程表示：

(39)

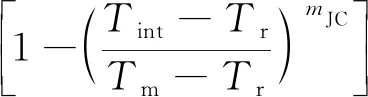
(40)

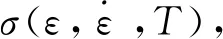
在計算切屑形成力時,假設刀尖是完全鋒利的,而實際加工過程中刀尖通常設計為具有一定半徑的圓弧以提高刀具壽命,此時刀尖與已加工表面接觸產生犁削力。如圖3所示,采用Waldorf等[22]提出的滑移線場模型用來預測由于刀尖鈍圓作用產生的犁削力。

如圖3所示,扇形區的角ηplow、θfan和γplow由幾何和摩擦關系得

BC=Rfan/sinηplow

(41)

ηplow=0.5arccosμplow

(42)

(43)

(44)

式中：μplow為摩擦因子,取為0.99[23]；ρplow指刀刃半徑re導致未加工凸起部分與水平面的夾角,設置為10°[23]；扇形區扇形半徑Rfan計算公式為

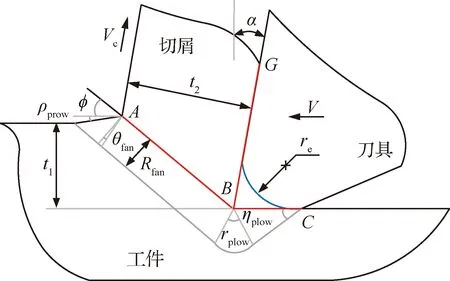
圖3 犁削滑移線模型Fig.3 Model of slip-line field for plowing

(45)

已知剪切角和剪切面的流動應力,用式(46)和式(47)可求得犁削力。犁削力被分解為沿切削方向的犁削力Pc和垂直于切削方向的犁削力Pt：

Pc=KABwBC[cos(2ηplow)cos(φ-γplow+ηplow)+

(1+2θfan+2γplow+sin (2ηplow))·

sin(φ-γplow+ηplow)]

(46)

Pt=KABwBC[(1+2θfan+2γplow+sin(2ηplow))·

cos(φ-γplow+ηplow)-cos(2ηplow)·

cos(φ-γplow+ηplow)]

(47)

總切削力由切屑形成力和犁削力疊加而成。在切削方向上的總切削力Fx和垂直于切削方向的力Fy表示為

(48)

3 非等分剪切區建模

在Oxley的預測加工理論中,解決了材料塑性變形過程中加工硬化和熱軟化的影響,然而,應變、應變速率和溫度都是根據平均值計算的。雖然這些參數的分布對描述介質連續流動是必不可少的,但Oxley模型沒有考慮到這些參數的分布。該部分以前一節的預測為基礎,對剪切區應力場和溫度場分布進行了預測,如圖4所示,在非等分剪切區(Unequal division shear zone, UDS)的框架下,建立了一種基于唯象的非線性剪切應變率分布模型。

研究人員從落刀實驗分析中發現,剪切帶被AB分成兩個不等的區域,其中下區域(CD到AB)比上區域(AB到EF)寬。Astakhov等[24]得出,在較寬的下區域和較窄的上區域,剪切應變速率隨速度的演化呈現不同的變化趨勢。

根據Pang[21]的研究,以剪切區質點位置ys

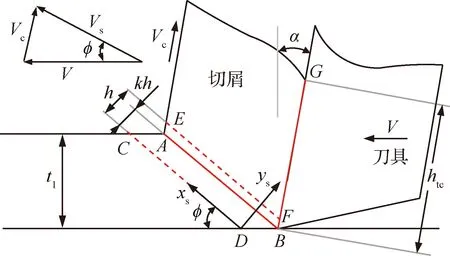
圖4 非等分剪切區模型Fig.4 Unequal division shear-zone model

和剪切區厚度h表示的四階多項式曲線可以描述剪切應變率在主剪切帶的分布

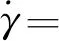
(49)

其中需要確定的系數為D1、E1、F1、d1、e1、f1[21]。

由圖4分析可知,若k定義為變形區下半部分占總厚度的比例,則主剪切區速度場和剪切應變率場的邊界條件為

1) 初始剪切區被AB(ys=kh)不均勻地分為寬區和窄區。

2) 塑性變形量取決于垂直主剪切帶的距離ys。

3) 在主剪切區的AB處切向速度為零(Vxs|ys=kh=0)。

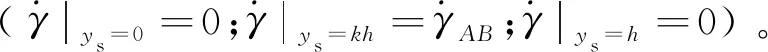
5) 由于材料顆粒以恒定的速度向主剪切區移動,在到達下邊界CD之前,速度和相應的剪切應變率的變化率為零,同樣,通過上邊界EF后,顆粒的應變率再次下降到零。假設應變率分布由光滑的可微曲線來表示,則在CD和EF邊界,需要有一極薄的緩沖帶,剪切應變率相對于ys的梯度為零。此外,假定曲線的可微性導致剪切應變率相對于ys的梯度在AB上也為零,剪切應變率達到最大值,即

(50)

通過以上分析,可以得到剪切區剪切應變率和速度分布如式(51)和式(52)所示:

(51)

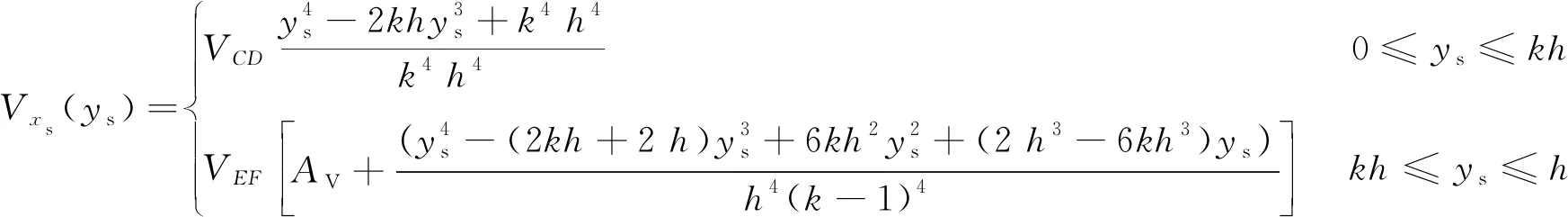
(52)

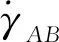
(53)

(54)

在非等分模型中,剪切應變的分布根據速度與剪切角的關系進行計算

(55)

在以上解析建模中,需要使用Oxley模型的輸出變量：剪切角φ、第一變形區剪切帶長寬比COxley和長度LAB、剪切面的平均溫度TAB。剪切角用于坐標系的角度計算和定位,COxley和LAB用于計算非等分剪切區厚度h,平均溫度用于迭代計算溫度和流動應力在剪切區厚度方向的特征分布。

導致主剪切區溫度升高的熱量可分為兩部分,一個是熱傳導,另一個是熱擴散。導熱反映了物體之間的傳熱,代表了導熱能力。然而,熱擴散在不同工況下表現不一致,我們假設熱擴散的比例是R。主剪切區中的熱量來源于加工過程中的塑性變形,因此,在主剪切區中任何垂直于ys軸方向的微平面上,單位時間內產生的熱量可以確定為

(56)

式中：τ為剪切應力。

在剪切區任何垂直于ys軸的微平面上,熱擴散對溫升的影響為

(57)

根據Zhou等[25]的研究,因傳質傳熱所引起的溫度分布可以根據邊界條件結合式(57)進行轉換,所以沿ys軸方向溫度分布的分段函數為

T=

(58)

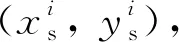
4 實驗與分析

4.1 實驗過程

在上述分析的基礎上,為了驗證本文模型的可行性,開展了直角切削實驗,觀測了6061-T6鋁合金的切削力及切屑微觀結構,6061-T6鋁合金的模型參數和物理性能參考文獻[7]。

直角切削方案示意圖如圖6(a)所示,棒材尺寸為?200 mm×80 mm,首先對棒材進行切槽加工,槽寬和槽深均為5 mm,得到12組寬約3 mm的環形凸起表面,然后對每一組外圓表面進行直角車削,切槽和切外圓均在數控車床型號為C6136HK的車床上進行。刀具寬度為5 mm的硬質合金切槽刀,使用Alicona刀具形貌觀測儀器測量了切槽刀具的刀尖鈍圓半徑,如圖6(b)和6(c)所示,為刀具A和B的刃口形貌和結構示意圖,其中刃口形貌的云圖表示刀具質點距離基準點的高度。

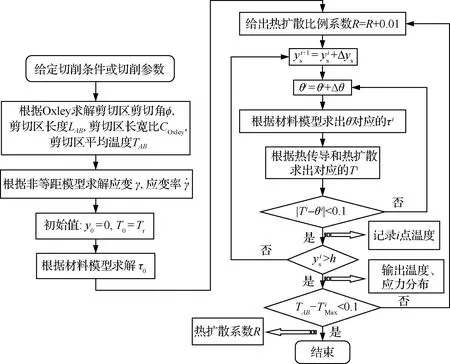
圖5 PSZ的R和溫度分布的求解流程圖Fig.5 Flow chart of solving process of R and temperature distribution in PSZ

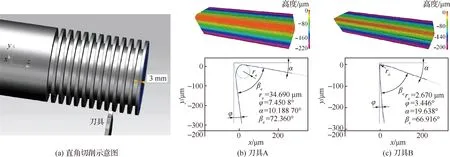
圖6 直角車削和刀尖結構示意圖Fig.6 Schematic diagram of orthogonal turning and edge structure

如圖7(a)所示,采用KISTLER壓電測力計9257B安裝在機床刀架上,用于測量車削過程中三個方向的切削力,每組實驗重復三次,計算其平均值。為了驗證模型并分析切削參數對切削力的影響規律,設計了12組實驗,實驗設置如表1所示。第8組實驗觀測的切削力如圖8所示,其中圖8(a)為切削力的原始數據,圖8(b)為濾波后對應的數據,可以看出測量的切削力數據較為平穩,相對于切向力Fx和徑向力Fy,軸向力Fz近似為0,所以忽視不計,可以將切削過程近似為直角切削,用來驗證切削力模型,我們分別觀測了兩種刀具在不同切削速度和切削厚度下的切削力數據。

材料在高溫塑性變形時,擴散機理占重要作用,而切削大多數金屬材料時,切削溫度相對于熔點較低,所以變形機制主要有位錯滑移和孿生變形。為了分析6061-T6鋁合金切屑變形中是否有孿生,如圖9所示,對第3組實驗的切屑進行離子減薄,使用透射電子顯微鏡(Transmission Elec-tron Microscopy, TEM)觀測塑性變形狀態,并對其進行選區電子衍射(Selected area electron diffraction, SAED)。根據Atmani等[26]和Wu等[6]的研究顯示,當金屬材料經過變形區形成切屑后,從自由表面往刀-屑接觸面方向上的較寬切屑厚度范圍內的微觀組織具有一定的均勻分布特性,切屑在較寬的面積內的位錯密度和晶粒尺寸的演化主要發生在剪切區內,所以采集的切屑TEM是切屑自由表面到刀-屑接觸面的中間區域。

圖7 加工實驗Fig.7 Machining experiment

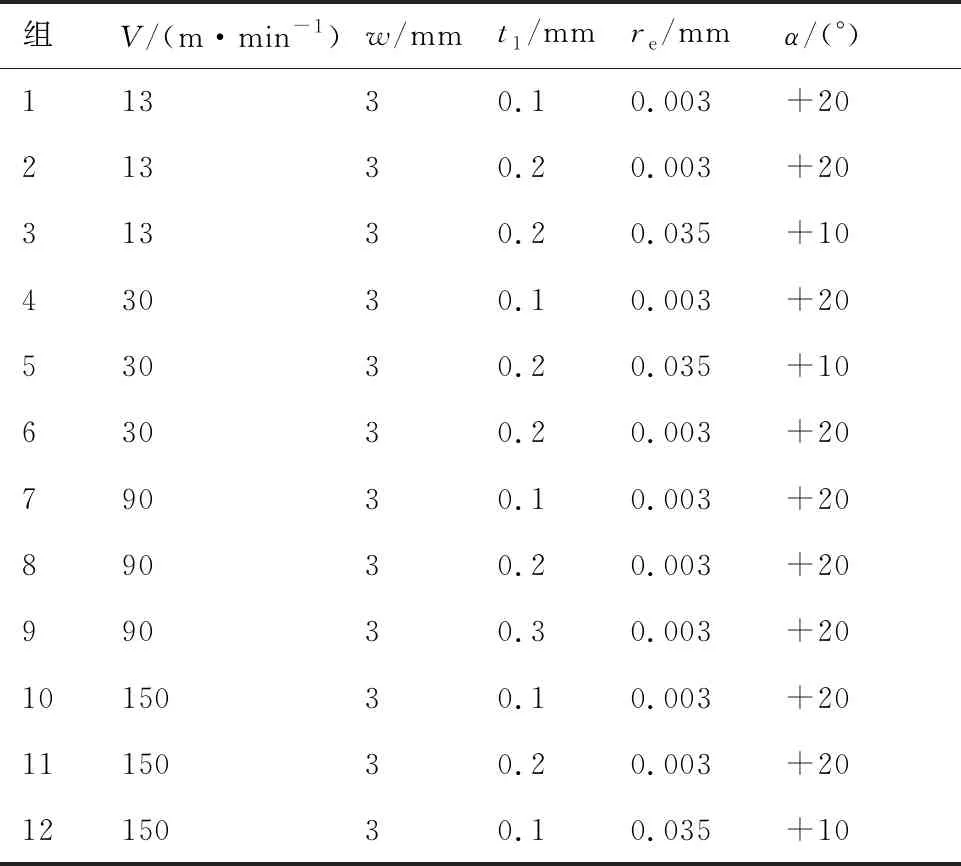
表1 直角車削參數Table 1 Parameters of orthogonal turning

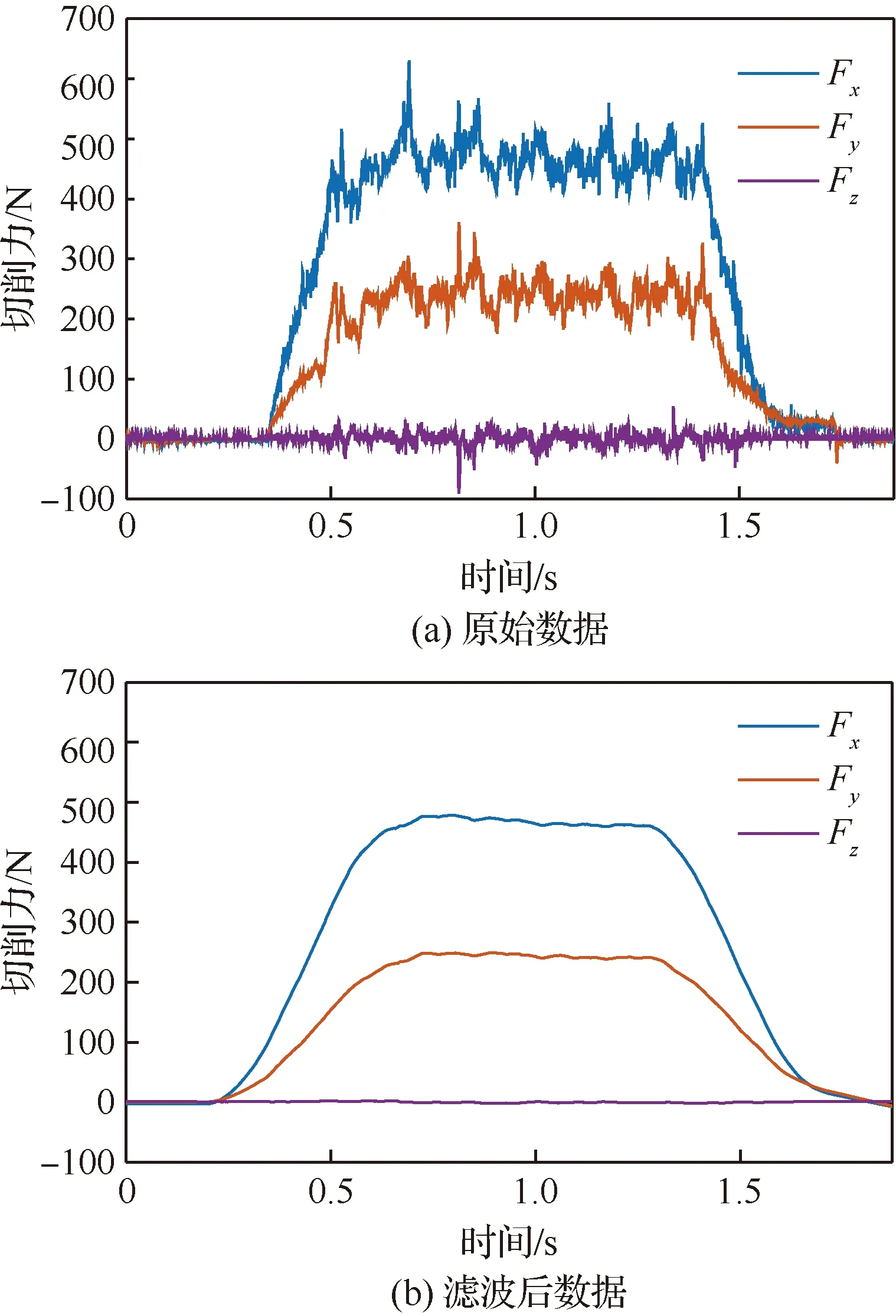
圖8 切削力數據(V=90 m/min, t1=0.2 mm)Fig.8 Data of cutting force (V=90 m/min, t1=0.2 mm)

如圖9(a)和圖9(b)所示,切屑內呈現典型的塑性變形狀態,位錯密度較高,部分區域為位錯胞構成的片層結構,并包含了大量位錯塞積形成的位錯墻。圖9(c)和圖9(d)為A1和A2區域的SAED,通過標定分析,并未發現孿晶的存在,因為面心立方結構的6061-T6鋁合金表現為高層錯能材料,擁有較高的堆垛層錯能,不會輕易出現孿生變形,位錯運動是其主要的塑性變形方式,這也證實了基于位錯密度的材料模型適用于反映材料冷加工變形的微觀結構變化與宏觀的力學行為之間的聯系。切削過程中,材料流經第一變形區時,剪切應變逐漸增大,由于純剪切變形的作用,材料中的粗大晶粒發生剪切和破碎,使原來粗大的晶粒沿剪切變形方向被拉長成條帶狀,同時晶體中的增殖源處位錯數量自發增多,Frank-Read位錯源是位錯增殖的主要機制[27]。

4.2 預測結果分析

4.2.1 等分模型預測結果分析

觀測和預測的切削力如圖10所示。從整體上可以明顯看出,結合JC模型預測的切削力和結合DDM預測的切削力均較好地反映了切削力隨參數組合的變化。圖10 (a)為預測的切向力,12組切向力預測值的平均百分比誤差分別為6.2%和4.9%。圖10(b)為預測的徑向力,JC模型和DDM模型預測值的平均百分比誤差分別為11.5%和7.8%。

在改進的Oxley模型的迭代求解過程中,中間輸出變量較為復雜,系統性的求解過程決定了最終的切削力值。考慮金屬材料冷加工中的微觀結構的變形行為時,主要以位錯運動為塑性變形機制引入到模型的求解過程。盡管之前唯象模型是模擬金屬成形過程中涉及高應變、應變速率和溫度效應的最常用模型,但是,本文結合位錯密度模型和Oxley預測加工理論得到的切削力相對于結合唯象的JC模型更加準確。Liu[4]指出在材料模型中包含大量相關的底層微尺度變形機制時,將在校準范圍之外產生更準確的預測。當應變和溫度分別在0.1～3和25～250 ℃之間,應變率分別取100 1/s和5 000 1/s時,JC模型和DDM模型的應力-應變曲線如圖11所示。可以從圖中看出兩種材料模型的應力-應變關系較接近。這說明更多涉及金屬位錯機制的物理模型可以更好地描述在類似于機械加工加載條件下的工作材料力學行為。

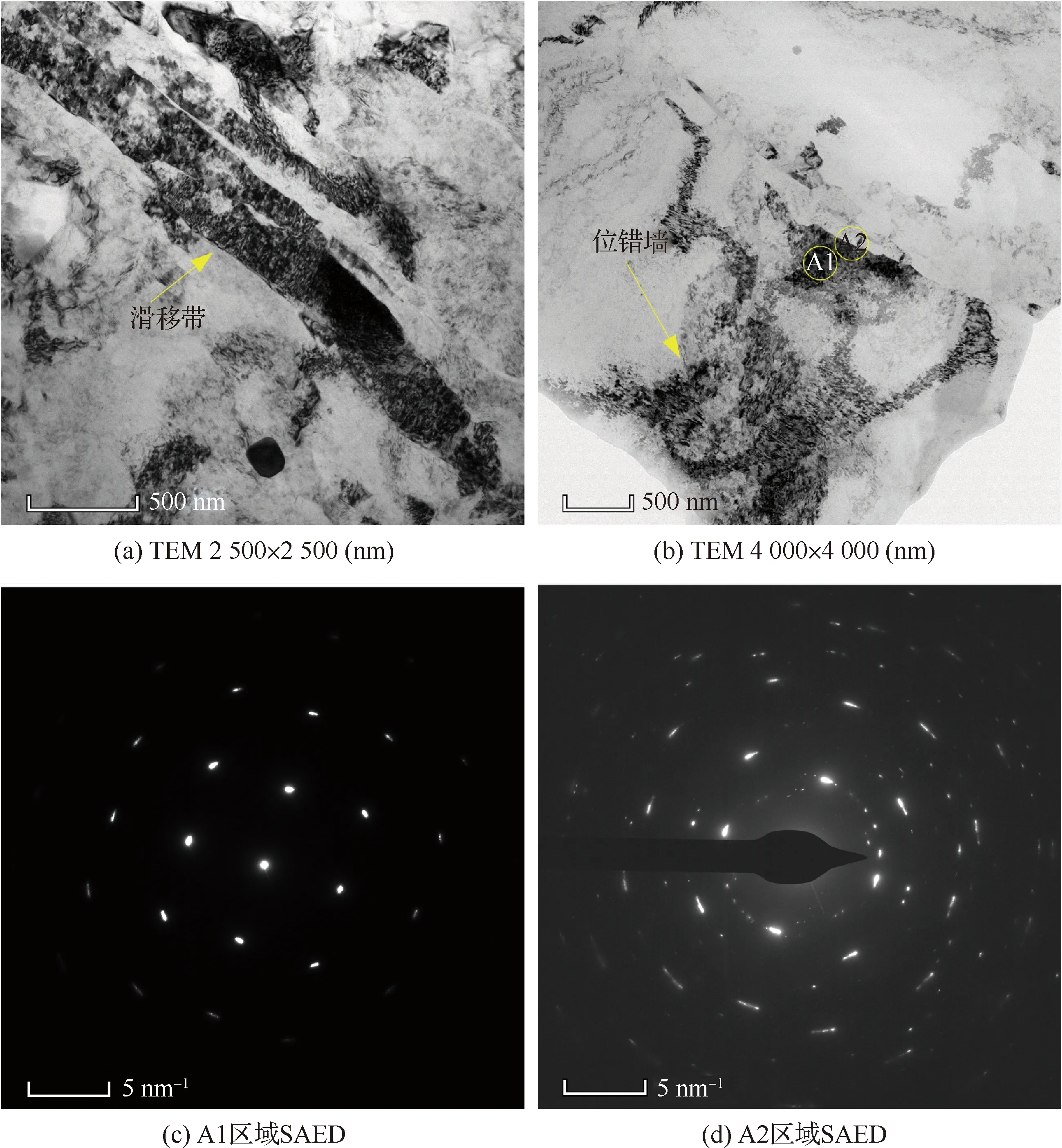
圖9 切屑的TEM明像場和A1、A2區域的SAEDFig.9 TEM bright field image of chip and SAED in regions A1 and A2

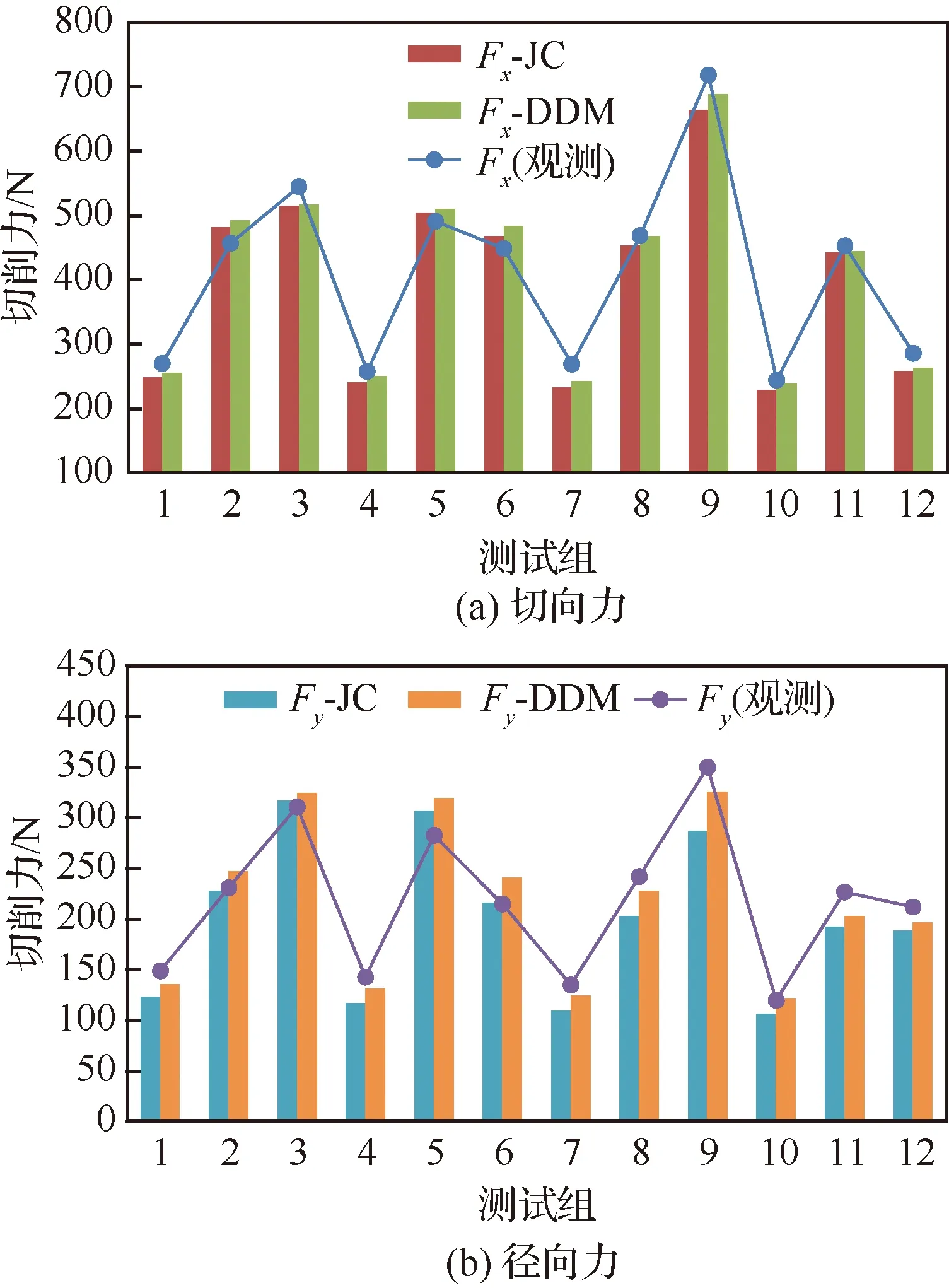
圖10 切削力的實驗值與預測值Fig.10 Experimental and predictive values of cutting forces

在改進的Oxley 模型中,工件材料特性和切削參數為輸入變量時,輸出的結果包括φ、COxley、LAB、δ、TAB、Tint、εAB和εint等,如表2所示,為模型求解得到的6組不同切削深度(第7、8和9組)和切削速度(第1、4、7和10組)下的過程變量。從表中可以看出,剪切角隨切削速度和切削深度的增大而增大,同時刀-屑接觸區的平均溫度高于剪切區平均溫度,刀-屑接觸區的應變大于剪切區應變,這是因為刀-屑接觸區受到強烈的摩擦擠壓作用導致[28-29]。

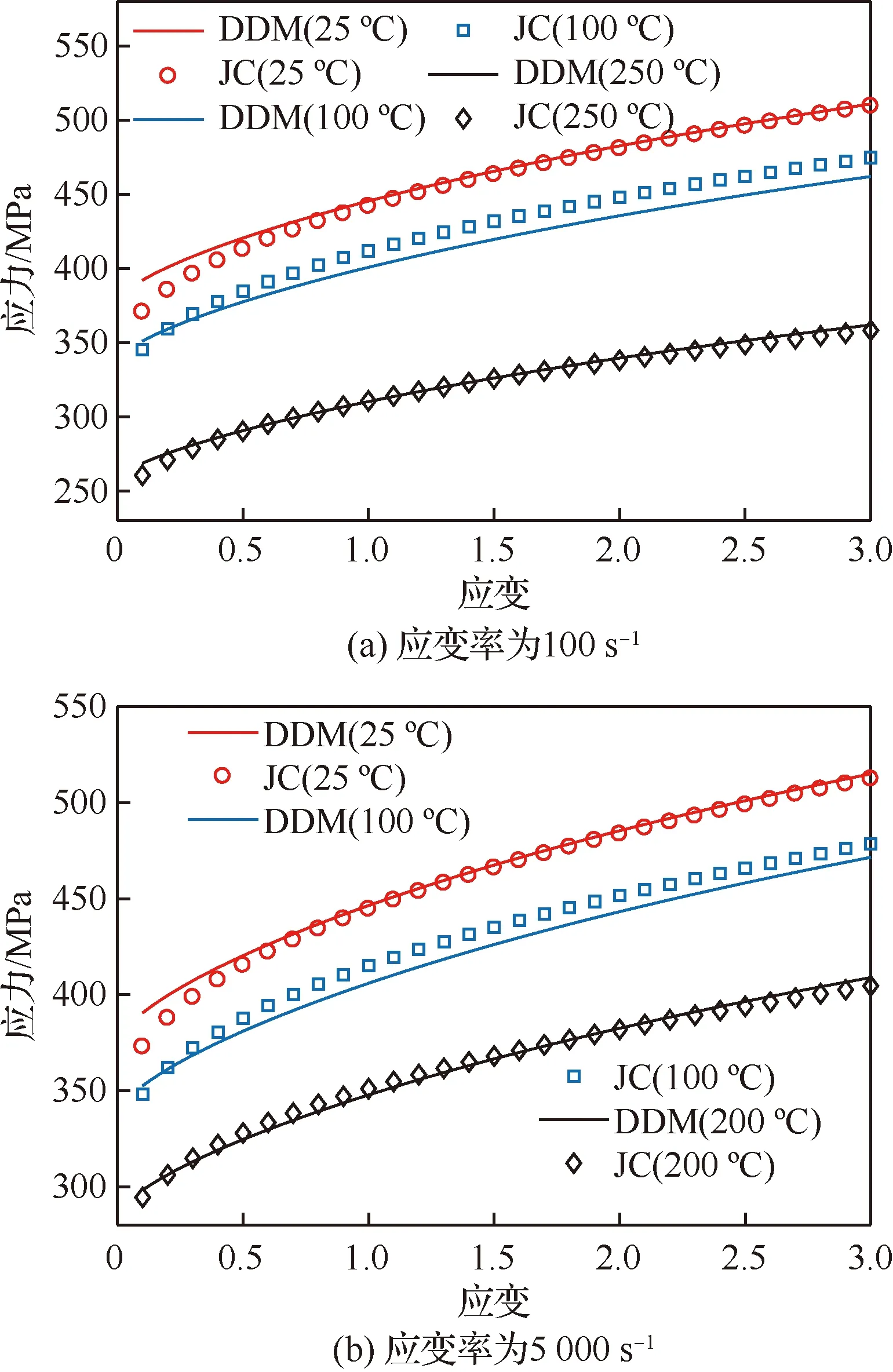
圖11 6061-T6鋁合金應力-應變曲線Fig.11 Stress-strain curves for 6061-T6 aluminum alloy

從表2中Oxley的計算結果可知,當切削深度增大,剪切區長度變長,然而剪切區和刀具-切屑摩擦區的溫度升高并不顯著。雖然剪切角增大和溫度升高可能會導致切削力降低,但是由于增大切削深度導致材料去除率增大,直接影響到切削變形和刀具和切屑摩擦的增大[30],較長的剪切帶導致參與位錯滑移的材料增多,消耗的變形能將會更多,所以增加了能量的消耗導致切削力的增大。當切削速度增大,剪切角增大、變形區溫度升高、剪切區和摩擦區應變降低,剪切區和摩擦區溫度升高的趨勢比切削深度引起的趨勢更為明顯,同時材料去除體積并未發生改變,由于應變降低引起剪切區位錯增殖數量減少,位錯密度降低[7],剪切區溫度升高導致位錯的湮滅作用增加,合金中位錯的運動能力增加,動態軟化加劇,從而降低了剪切區流動應力[31],所以切削速度增大導致切削力降低是多種過程變量共同作用的結果。

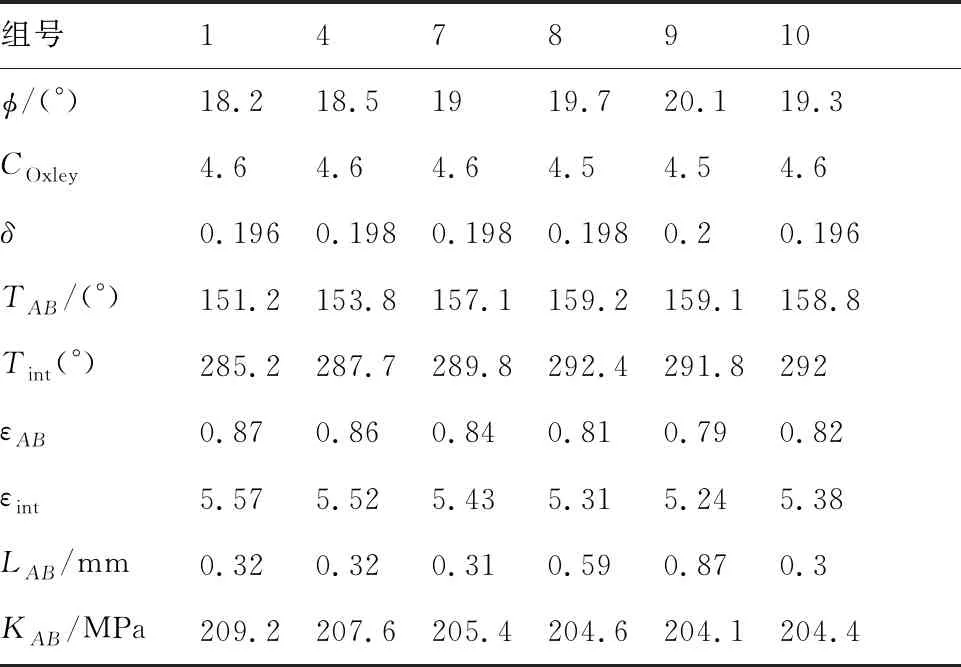
表2 改進Oxley模型的計算結果Table 2 Results of improved Oxley model

4.2.2 非等分模型預測結果分析

求解得到的3組切削速度(第4、第7和第10組實驗)下的溫度和剪切應力分布如圖12所示,從剪切帶入口到剪切帶出口位置,溫度逐漸增大然后趨于穩定,增大切削速度,剪切區溫度升高。應力先逐漸增大后緩慢降低,過剪切區后急劇降低。

當材料質點經過剪切區低溫階段時,切削速度越大,剪切應力越大,這是因為剪切應變速率隨著切削速度的增大而增大,動態力學行為關系表明,應變速率越大,位錯增殖的數目增多,位錯運動的速度加快,位錯間的相互交割幾率增大,以致變形時的臨界切應力大幅提高。然而,當質點到達高溫區域,由于受到熱軟化的影響,位錯的湮滅作用增加,合金中位錯運動能力增加,軟化效應加劇,導致切削速度大的流動應力反而低一些。除此之外,從圖12還可以看出較低的切削速度下,剪切區厚度h相對較厚,工件材料受到更多的時間和空間范圍內外力的作用,所以切削速度降低會導致切屑內應力總體上增大。

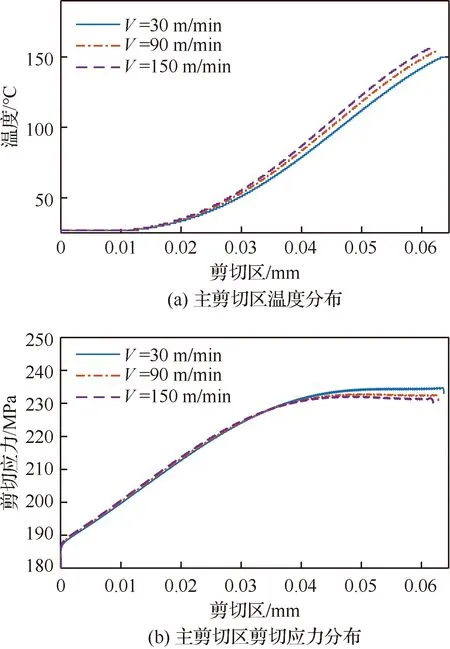
圖12 主剪切帶溫度和剪切應力分布Fig.12 Distribution of temperature and shear stress in shear zone

根據非等分剪切區模型計算的剪切應力值,得到切削力預測值如圖13所示,模型預測的切削力較好地反映了切削力隨切削參數的變化,12組預測值的平均百分比誤差分別為5.9%和7.3%,預測精度與平均值模型不一致,這可能是因為多個模型之間的誤差累計導致,但是非等分模型預測的切削力的整體趨勢與觀測值吻合較好,這對于預測剪切區微觀結構演化的參數輸入(應變場和溫度場分布)至關重要。通過迭代得到的剪切區熱擴散的比例R如圖13的次縱坐標所示,R值在0.2～0.3之間,其隨著切削速度和進給的增大而增大,隨著前角的增大而減小,這是因為熱擴散的比例R隨著溫度的升高而增大導致。

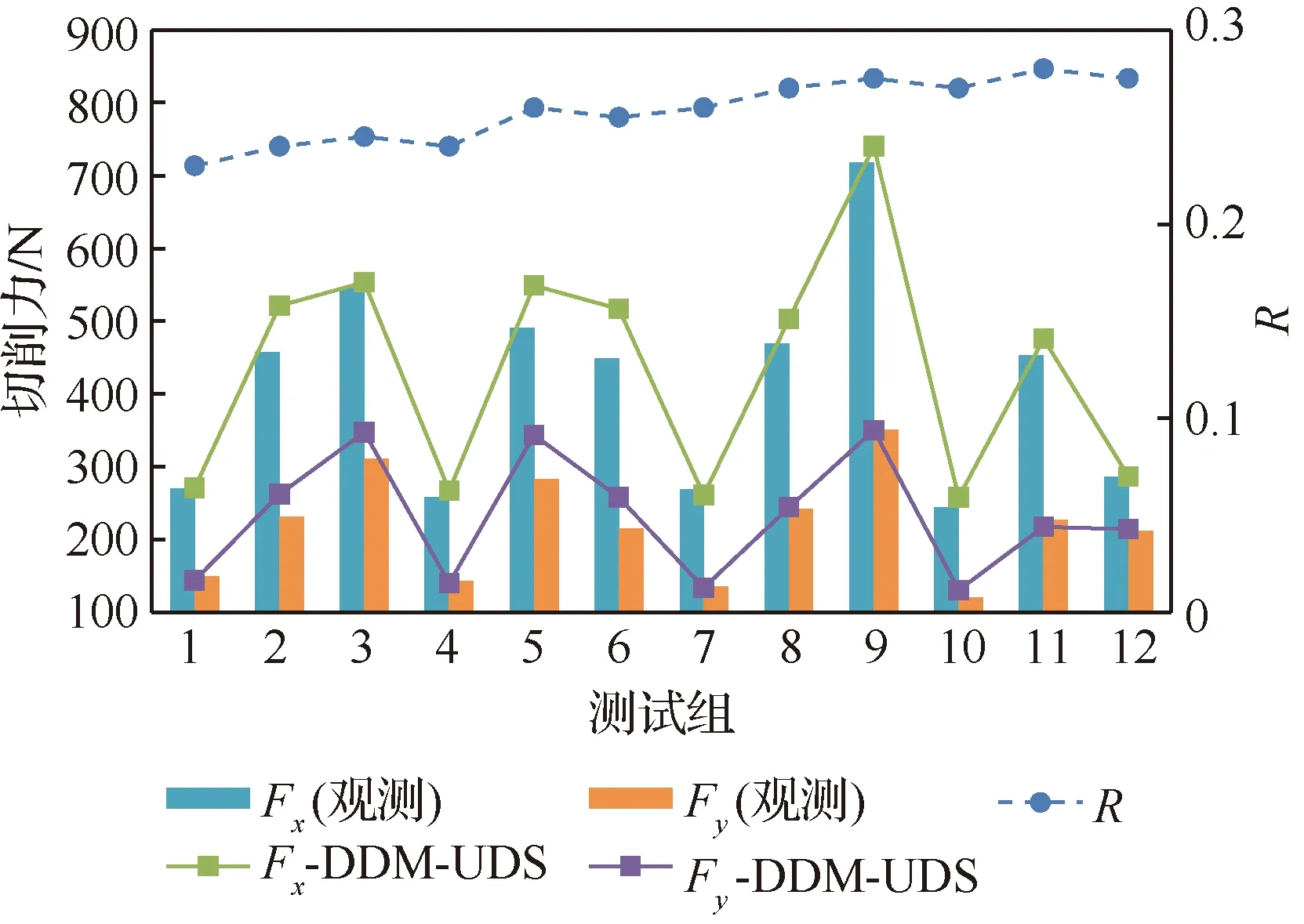
圖13 非等分剪切區模型的切削力和R的預測Fig.13 Prediction of cutting force and R for unequal division shear zone model

4.2.3 解析模型與有限元模型的比較

在第7組實驗切削參數下(V=90 m/min),使用Deform有限元軟件建立了切削仿真模型,首先將刀具固定,然后工件往切削速度相反方向運動,為了避免刀尖周圍的大變形導致的網格畸變,將網格結構視為四面體,使用拉格朗日網格技術對工件進行網格劃分,熱傳導系數和摩擦系數使用Deform專業切削模塊推薦的0.02 m2·s·K和0.6,材料模型為JC模型,參數來源文獻[7]。

在有限元模型的未切削厚度層上定義了6個跟蹤點,如圖14(a)所示,觀察到剪切區溫度和剪切應力的變化過程如圖14(b)和圖14(c)所示,6個跟蹤點的最大溫度范圍在140～165 ℃之間,最大剪切應力范圍為224～237 MPa。解析模型預測的溫度和剪切應力分布如圖12所示,最大溫度約為150 ℃左右,最大的剪切應力值約為230 MPa,本文預測的剪切區溫度和剪切應力的最大值與有限元模型預測的結果較接近。

為了比較解析模型與有限元模型的精度,使用有限元模擬了不同的切削深度(第7、第8和第9組實驗)下的切削力值,得到如圖15所示的仿真結果對比,其中Error_Fx-SIM和Error_Fy-SIM是3種解析模型的平均百分比誤差的平均值,Error_Fx-FEM和Error_Fy-FEM是有限元預測的百分比誤差,3種解析模型得到切削力值在整體上預測精度優于有限元。有限元預測的徑向力隨著切削深度的增大而降低,趨勢與實驗值相反,Javidikia等[32]在有限元預測時也得到了相似的結果,而解析模型預測的切削力與實驗值的趨勢一致。獲取穩態切削時的切削力值時,有限元預測時間為4～6小時,而3種解析模型預測切削力需要1～5分鐘。其中耗時最少的為第1種,Oxley模型與JC模型的結合。其次為第2種,Oxley模型與DDM模型的結合。最后是第3種,等分剪切區和非等分剪切區的結合。因為JC模型計算材料行為時,計算量較少,如式(30)所示。而DDM考慮的因素較多,如式(1)～式(12),非等分模型計算切削力在等分模型的基礎上還需要式(36)～式(45)迭代計算。但是,正是因為考慮了更多微觀結構影響和剪切區非等分的分布特性,使得第2種模型和第3種模型的切削力預測精度分別得到了提高。

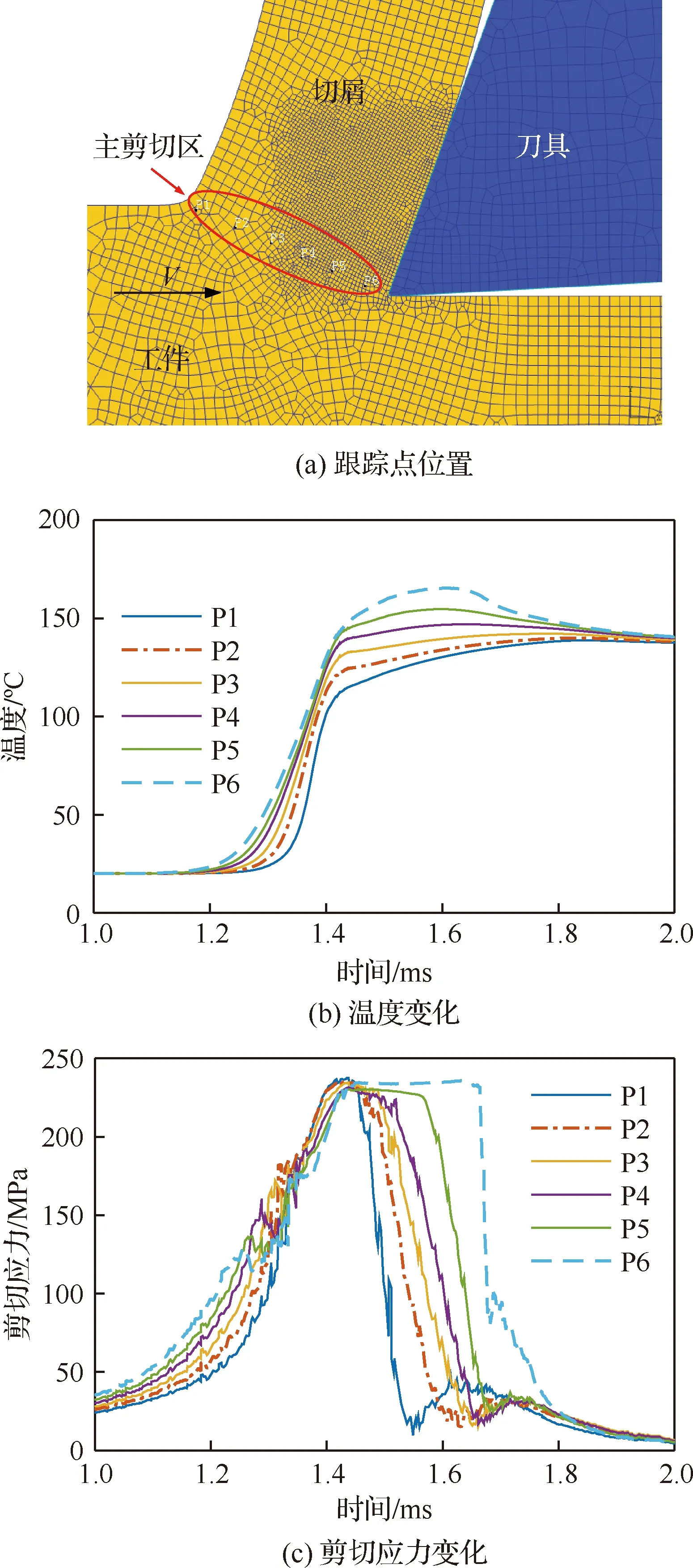
圖14 有限元仿真模擬的溫度和剪切應力Fig.14 Temperature and shear stress simulated by finite element simulation

4.2.4 剪切區微觀結構演化預測

在切削大塑性變形過程中,由于第一剪切區剪切變形作用,應變的大量累積以及由此引入的一系列位錯運動是切屑晶粒細化的主要原因。微觀結構的變化與位錯密度密切相關,可以通過DDM方法[7]進行解析分析,結合Oxley剪切區等分模型和非等分模型計算的應變場、溫度場,可以建立剪切區微觀結構演化解析模型。

圖16為第3組實驗切削6061-T6鋁合金的主剪切區微觀結構演化過程,當材料質點從入口邊界處進入剪切區并經過剪切變形后到達出口邊界,切屑位錯密度達到了2.8×109mm-2,平均晶粒尺寸細化到569 nm,通過實驗觀測得到的晶粒尺寸為591 nm,實驗初步驗證了模型的可行性。材料在最初未受到剪切時,材料變形并不均勻,組織中的晶粒也大小不一,由于純剪切變形的作用,材料中的粗大晶粒發生剪切和破碎,使原來粗大的晶粒沿剪切變形方向被拉長成條帶狀晶粒,如圖9(a)所示,同時,應變逐漸增大導致材料中大量位錯出現在晶粒內,由于位錯運動形成亞晶界,此時剪切變形作用對晶粒細化起主要作用,隨著應變的增加,晶粒逐漸細化,局部組織中出現了少量細小的等軸晶,但晶粒的大小和形狀不均勻。通過剪切區后,回復作用逐漸明顯,位錯的增殖和湮滅將達到動態平衡,晶粒的大小基本上不再變化。

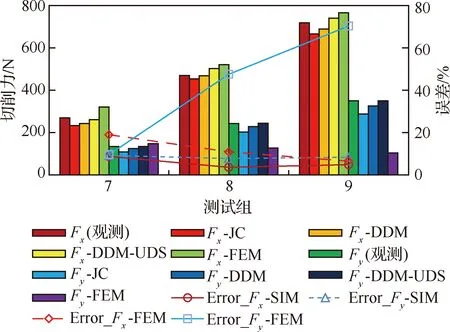
圖15 不同模型的切削力對比Fig.15 Comparison of cutting forces of different models

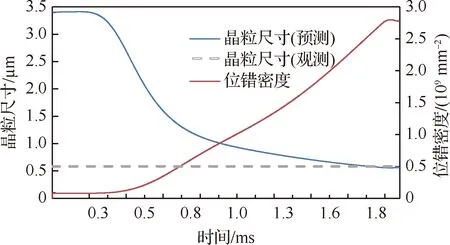
圖16 剪切區位錯密度和晶粒尺寸的演化Fig.16 Evolution of dislocation density and grain size in shear zone

5 結 論

1) 以位錯運動為塑性變形機制引入到預測加工理論的切削力求解過程,得到了與經典切削理論相一致的力學行為且產生了更為準確的結果。

2) 當切削深度增大,切削力增大的主要原因是由于剪切區長度變長導致參與位錯滑移的材料增多。增大切削速度導致切削力的降低不是單一變量引起的,而是剪切角增大、剪切區溫度升高和變形區應變降低的共同作用結果。

3) 非等分剪切區模型正確反映了第一變形區溫度和應力的分布特征,且與二維有限元模型分布相一致,通過實驗觀測初步驗證了微觀結構演化模型在解析切屑內位錯密度和晶粒尺寸演化過程的可行性。