基于動力學RRT*的自由漂浮空間機器人軌跡規劃

葛佳昊，劉莉，董欣心，田維勇，陸天和

北京理工大學 宇航學院，北京 100081

隨著人類對宇宙空間探索的不斷深入，高效的后勤保障成為空間在軌服務的熱點方向之一[1]，空間機器人成為低成本在軌運行的關鍵[2]。根據機器人基座的控制策略不同，可將空間機器人分為基座位姿固定、基座位姿機動、基座姿態受控和自由漂浮等模式[3]。自由漂浮空間機器人因節省燃料、姿態調整靈活等優點，有更高的實際應用價值，其軌跡規劃問題是關鍵技術之一。

自由漂浮空間機器人(Free Floating Space Robot，FFSR)軌跡規劃即對機械臂末端機械手的運動軌跡規劃，需要在滿足多體動力學系統動力學特性和非完整約束條件的同時避開障礙并到達目標位置，FFSR工作環境比地面機器人更為惡劣，軌跡規劃更為復雜。關于FFSR模型，Vafa和Dubowsky[4]提出了基于虛擬機械臂(Virtual Manipulator，VM)的分析建模方法，實現了對FFSR運動/動力學方程的更簡易描述。Dubowsky和Papadopoulos[5]建立了完整的自由飛行和自由漂浮機器人運動/動力學和控制模型。梁斌等[6]提出動態等效機械手(Dynamically Equivalent Manipulator，DEM)的概念，將FFSR轉化為基座鉸接的機械臂，以克服VM不能直觀模擬空間機械臂的缺點。

根據規劃模型的不同，FFSR的軌跡規劃可大致分為基于運動/動力學模型規劃和基于幾何模型規劃兩類。

基于運動學模型的規劃通常借助智能算法對FFSR軌跡規劃進行求解，如粒子群優化算法[7-9]、遺傳算法[10-11]和差分進化算法[12]等智能算法被用來規劃得到單臂和雙臂機器人運動軌跡；黃興宏等[13]將非完整約束軌跡規劃問題轉化為最優控制問題，并采用牛頓迭代法得到全程恒定基座姿態零擾動的空間機械臂軌跡。基于運動學和動力學模型，FFSR軌跡規劃問題通常轉化為最優控制問題，戈新生和陳凱捷[14]采用Legendre偽譜法實現機器人軌跡規劃；曾祥鑫[15]通過高斯偽譜法得到機器人移動軌跡，并以此為輸入實現考慮機械臂撓性的FFSR姿態控制。基于DEM模型，Benevides和Grassi[16]引入雙向策略的快速擴展隨機樹(Rapidly-exploring Random Tree, RRT)算法得到等效機械手的無碰撞軌跡，但是難以還原成FFSR的關節運動情況。Xu等[17]針對旋轉目標的抓取問題，提出面向區域捕獲的雙臂空間機器人協調路徑規劃方法。至此，考慮高維非完整約束的FFSR軌跡規劃問題已得到基本解決，但現有方法還存在著規劃效率較低的問題。

另一類為僅考慮機器人幾何模型的快速路徑規劃。賈慶軒等[18]采用A*算法實現了對機械臂軌跡的毫秒級避障規劃，滿足控制周期的實時性要求。陽涵疆[19]和鄒宇星[20]等基于機械臂關節構形空間，分別采用RRT和改進的概率路線圖法實現了對六自由度機械臂的無碰路徑規劃。謝碧云等[21]改進了雙樹隨機樹搜索算法的目標點樹根生成機制，在不考慮機械臂末端姿態的情況下，實現了對典型空間冗余機器人的路徑規劃。僅考慮幾何模型可以較快得到可行路徑，但規劃結果不滿足系統動力學特性。

為提高考慮運動/動力學模型的FFSR軌跡規劃效率，提出一種基于動力學RRT*算法的FFSR軌跡規劃方法。首先，將FFSR的運動/動力學方程偽線性化為機械手狀態方程，并設計同時考慮關節能量消耗和軌跡完成時間的代價函數。其次，為提高碰撞檢測效率，針對機械手初末位置間障礙，提出機械臂避障和機械手避障的兩層次避障策略，并設計FFSR動力學RRT*軌跡規劃器。最后，以2自由度(Degree of Freedom，DoF)自由漂浮空間機器人的軌跡規劃為例進行數值仿真。結果表明，采用動力學RRT*方法可在較少的迭代步數內得到可行解，隨迭代步數增加，可獲得漸進最優軌跡，具有較高的求解效率。

1 FFSR軌跡規劃問題假設及模型

選用單臂自由漂浮機器人通用模型，如圖1所示。圖中：CM為機器人的質心位置，并將其選為慣性系坐標原點；CMi為FFSR各部件的質心位置；Pi為第i個機械臂關節；ρi為各部件質心在慣性系的位矢；qi為各部件的相對轉角，正方向規定如圖1所示；ri為第i個部件質心到下一個關節的位矢；li為第i個部件質心到前一個關節的位矢。

圖1 單臂FFSR通用模型Fig.1 General model of single arm FFSR

1.1 FFSR模型

自由漂浮模式下，系統線動量、角動量守恒：

(1)

(2)

由式(1)和式(2)可得

(3)

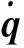
末端機械手的坐標可表示為

ρE=ρn+rn

(4)

對式(4)求導可得系統運動學方程為

(5)

式中：J(q)為FFSR的廣義Jacobian矩陣。

忽略重力，考慮系統拉格朗日方程和總動能：

(6)

可得系統動力學方程：

(7)

1) 忽略重力，忽略太陽風等阻力，FFSR始終動量守恒且初始動量為0。

2) 忽略FFSR部件撓度，各部件間由一個單自由度關節連接，每個關節僅受一臺電機控制。

3) 系統質量參數已知，運動狀態可觀測。

4) 基座質量遠大于機械臂桿質量，且FFSR運動緩慢，故當前節點的機器人位姿可作為到下一個節點間狀態的估計值。

1.2 系統線性化

由式(5)和式(7)可得

(8)

式中：H(q)為對稱正定矩陣，其逆矩陣必存在。

本研究結果也顯示，觀察組患者Baumann角、臨床效果、手術時間等均優于對照組，差異有統計學意義（P＜0.05），這是因為小切口輔助復位經皮克氏針固定治療中，切口能夠有效避免太靠上，減少對橈神經的損傷，同時術中能夠有效保護干骺端骨膜，從肱骨小頭進針會事先捫清確定尺神經溝，進而避免了因手術操作對尺神經的損傷，術后會依據情況予以患者抗生素或者引流。

(9)

假設4)保證每個節點之間都可近似為線性系統。

1.3 代價函數

選取以權系數μ∈[0，1]加權的Bolza形式性能指標作為代價函數，在應用過程中，可通過調整權系數使FFSR具有更大工作靈活性。代價函數為

minJ=μJ1+(1-μ)J2

(10)

式中：J為總代價函數；J1和J2分別為使位姿調整過程中能量消耗最小的Lagrange型性能指標和增強位姿調整的時效性的Mayer型性能指標：

(11)

(12)

式中：tf為機器人位姿調整最終時間；R為指定的正定常數矩陣，代表控制輸入成本的權衡；t0為系統初始時刻。

2 FFSR系統的避障軌跡規劃

FFSR是典型的非完整多體動力學系統，系統表現出的高維度和非完整特性增加了路徑規劃的難度與控制的復雜性。規劃時不應只考慮幾何避障，也應考慮系統動力學特性。

對于實際應用，強調軌跡規劃的效率和軌跡的可行性而非最優性。相比于圖搜索方法(如A*和D*等)、局部規劃算法(如人工勢場法等)和求解最優控制問題的偽譜法等，RRT*算法作為一種基于采樣的規劃方法，可通過重選父節點和重布線等操作降低路徑代價，有效提高算法效率，在考慮對象非完整約束限制的條件下，快速搜索解空間并得到可行軌跡，對FFSR軌跡規劃具有較高的適應性。因此，加入機器人動態約束的RRT*算法在收斂的時效性和高維問題求解的適應性方面獨具優勢。

2.1 最優軌跡的計算

對于能控線性質點系統，動力學RRT*算法[23]通過求得最短抵達時間的閉式解，構造末狀態固定、抵達時間自由的軌跡規劃問題，自由給定抵達時間以降低代價函數值。對于非線性系統，每次迭代時圍繞假定平衡點一階泰勒展開為能控線性系統。作為運動非線性強的多體動力學系統，采用上述方法不能準確描述FFSR運動狀態。

針對此問題，采用偽線性化方法得到解析的FFSR狀態空間模型，相比于文獻[23]，模型描述更精確，適用范圍更廣，迭代時只需代入新廣義關節角值即可更新模型，提升運算速度，使規劃過程更簡潔快速，規劃結果更加符合實際。

對于能控的離散動力學系統：

(13)

式中：u(t)為系統輸入；x0為系統初始狀態。

2.1.1 最優抵達時間求解[23]

對于末狀態x(tf)=x1固定、機器人位姿調整最終時間tf固定的最優控制問題，構造Lyapunov函數：

(14)

其閉式解為加權能控的Gramian矩陣：

exp(AT(t-t′))dt′

(15)

式中：t′為時間變量t之前的某時刻(t′

那么，最優控制輸入為

u(t)=R-1BTexp(AT(tf-t))d(tf)

(16)

將式(16)代入式(13)，得到代價函數的閉式解：

(17)

(18)

經式(18)計算得到最優的抵達時間，那么，原問題擴展為了末狀態固定且抵達時間自由的軌跡規劃問題。

2.1.2 最優軌跡的計算[23]

令y(t)=exp(AT(tf-t))d(tf)，則有：

u(t)=R-1BTy(t)

(19)

將式(19)代入式(13)，得到復合微分方程：

(20)

從而得到最優軌跡的狀態量與控制輸入為

(21)

(22)

至此，得到的狀態量和輸入量實現了對最優軌跡的唯一確定。

2.2 FFSR避障策略

僅考慮機械手初末位置間存在障礙的情況。Rybus[24]總結了空間機器人避障的發展現狀，為進一步簡化計算，將障礙物抽象成長方體(在2維空間內為矩形)；為保證運動安全性，對障礙物進行膨化作為真實障礙。

提出FFSR機械臂避障與機械手避障兩層次避障策略。若機械臂與障礙物干涉或機械手位于障礙物內部，則認為機器人與障礙碰撞。

2.2.1 機械臂避障策略

若每次通過求解機械臂幾何位置判斷是否與障礙干涉，會大大增加計算量，降低算法效率。因此，對于單臂自由漂浮機器人通用模型，結合工程應用實際，采用障礙幾何延拓的策略避免機械臂碰撞。

如圖2所示，對原障礙進行膨化，面a為膨化后障礙距離機器人最近的面，基于面a將障礙延拓至機械手可達最遠端。那么，原可行的軌跡a、b中僅有軌跡a可行。

圖2 機械臂的避障策略Fig.2 Obstacle avoidance strategy of robotic arms

2.2.2 機械手避障策略

如圖3所示，對原障礙進行膨化。機械手當前的位置為點1，E為點1與障礙四角連線的包絡區域，其他點為機械手下一狀態點xnew。點2位于E外，點3位于E內點1與障礙之間，點4位于障礙內，點5位于E內障礙后方。易得，位于點4、5時軌跡不成立。

圖3 機械手的避障策略Fig.3 Obstacle avoidance strategy of manipulator

2.3 動力學RRT*規劃器

將FFSR偽線性模型與兩層次避障策略融入動力學RRT*算法，使其具備對多體系統的規劃能力。設計基于FFSR多體運動學與動力學的RRT*算法求解器，以找到式(21)和式(22)定義的最優軌跡。通過較少的迭代次數獲得軌跡的可行解，隨著迭代次數增加，軌跡逐步趨向最優。

圖4為求解器節點生成及隨機樹更新示意圖圖中r為搜索子節點時設置的鄰域半徑。結合圖4，給出算法步驟流程如下。

步驟1設迭代次數k=1，xstart和xgoal分別作為軌跡的初末狀態點。

步驟2在第k次迭代時，在隨機樹上各狀態節點x處更新FFSR系統偽線性模型并獲得對應的代價函數值cost[x]，以x為父節點生成新的隨機狀態點xrand。

步驟3碰撞檢測。若發生碰撞，則重新生成隨機狀態點并進行步驟3；反之，設xrand為合法隨機狀態點xnew。

步驟5隨機樹重新布線。對已有狀態點及xgoal，在滿足避碰條件下，若cost[xnew,xnear]

步驟6判斷隨機樹是否已延伸至xgoal，若是，則可行軌跡生成，算法可停止；若否，則轉至步驟7。若希望完成全部迭代次數，則忽略步驟6，轉至步驟7。

步驟7根據節點間父子關系求解軌跡，更新隨機樹；k+1→k，轉至步驟2，如圖4(c)所示。

考慮到FFSR狀態方程的系統矩陣A為冪零矩陣，exp(At)可表達為一個n-1自由度的矩陣多項式；因此，由式(15)、式(17)、式(21)和式(22)可得到確定的閉式多項式解，最優軌跡可解析表達。那么，規劃得到的軌跡也可用多項式平滑連接。與經典RRT*算法不同的是，規劃過程中軌跡直接延伸至新的可用隨機點，而不是向新的可用隨機點前進固定距離，這樣可以快速連接初末位姿，得到可行軌跡，進而根據代價函數值更新或更新隨機樹以獲得更優軌跡。

圖4 節點生成及隨機樹更新示意圖Fig.4 Schematic diagram of node generation and random tree updating

迭代期間通過式(3)和式(23)求解機器人狀態信息：

(23)

為提高運算速度，算法采用Doolittle分解法對式(9)的H-1(q)進行求解。

3 仿真驗證與結果分析

為在驗證所提方法有效性的同時不失一般性，選取簡化的平面2連桿自由漂浮機器人作為研究對象，此模型能夠充分證明設計理論的概念和性能，已廣泛應用于空間機器人理論驗證[15]。

3.1 仿真參數和結果

系統的模型參數如表1所示。

表1 2連桿FFSR模型參數Table 1 Parameters of 2DoF FFSR model

仿真是基于PC機(3.41 GHz/Core8)上的MATLAB R2019b進行。仿真迭代次數選取1 000次。對μ=0, 0.5, 1.0這3種目標情況進行數值仿真。仿真結果如表2和圖5所示。

表2 迭代1 000次的規劃結果Table 2 Planning results of 1 000 iterations

結合表2，從系統沿軌跡規劃結果運動過程圖(圖5(a)～圖5(c)，采用FFSR部件顏色的由淺至深表明系統從起點運動到目標點的時序變化)上看，生成的軌跡光滑且滿足約束條件，能有效避開障礙，并以預設的狀態到達目標點。觀察可發現，能量消耗最低的軌跡最貼近障礙物，過程調整幅度最小；調整時間最短的軌跡偏離障礙物的距離最遠，過程調整幅度最大。其原因在于:為了使能量消耗最低，電機扭矩的數值和變化幅度小(圖5(g))，姿態變化幅度小，使得軌跡完成的時間長，軌跡貼近障礙；調整時間最短的軌跡則相反，電機的扭矩輸出和變化幅度較大，甚至到達扭矩的約束邊界(圖5(h))，FFSR姿態調整速度快，姿態調整幅度大(圖5(e))，使得軌跡完成的時間短，軌跡偏離障礙較遠；能量消耗和調整時間折中的軌跡規劃結果則在姿態調整幅度(圖5(f))、所需時間和電機扭矩輸出(圖5(i))等方面指標居中，符合代價函數設置預期。此外，對于不同權系數，初末位置關節角角速度和加速度近似為0，規劃結果符合工程應用需要。

圖5 能量消耗最低、調整時間最短和兩者折中時的軌跡、關節角和電機扭矩Fig.5 Path, joint angle, and motor torque with minimum energy consumption, minimum adjusting time, and tradeoff between energy consumption and adjusting time

3.2 仿真結果分析

3.2.1 漸進最優性

為了驗證規劃方法的漸進最優性，選取上述代價函數權系數μ=0.5的算例(迭代次數1 000 次)，最終代價函數值為2.901 6。代價函數值隨迭代次數增加的變化情況如圖6所示。結果表明，代價函數值隨迭代次數的增加逐步降低，可得到從初始位姿到期望位姿的漸進最優調整軌跡。

圖6 代價函數值與迭代次數的關系Fig.6 Cost function value versus number of iterations

3.2.2 算法有效性

在實際應用時，通常不需要最優軌跡而是快速得到可行軌跡。如圖6所示，在第13次迭代時，生成了有效的代價函數值，即此時生成了可行的軌跡。根據式(23)，最初得到的軌跡誤差較大，隨著迭代次數的增多，路徑上隨機點數增多，誤差逐步降低。值得注意的是，快速隨機擴展類方法的隨機性影響了生成可行軌跡的迭代次數，但是經多次計算，在此場景下，算法迭代35次以內可得到可行軌跡，且單次迭代時長約0.61 s。

3.3 算法對比

選取經典RRT*算法、高斯偽譜法與本文算法對比。本文算法與高斯偽譜法均包含系統動力學模型，代價函數選為姿態調整時間最短；而經典RRT*算法僅能考慮FFSR的關節幾何約束，不包含動力學信息，難以獲取姿態調整時間及能量消耗，代價函數為路徑最短。將三者結果進行對比，自由漂浮機器人的初末位姿與障礙物特征相同。其中，經典RRT*算法節點數為分別為3 500與5 000，步進長度為0.005 m；高斯偽譜法的配點數分別為20與30。

圖7為各方法規劃得到的末端機械手路徑對比，由對比可得，高斯偽譜法可得到規劃的最優解；經典RRT*規劃得到的路徑更短，但是由于無法考慮系統動力學特性，因而規劃得到的路徑不平滑，難以滿足系統動力學約束，不能保證運動的連續性。

圖7 不同方法機械手軌跡規劃結果對比Fig.7 Comparison of trajectory planning results of manipulator with different methods

以同樣仿真情景和硬件環境下規劃所需的CPU計算時間為規劃效率的評價標準，各方法的規劃效率及代價函數值展示于表3。

由表3可得，動力學RRT*算法可以快速生成可行軌跡；經典RRT*算法只生成路徑而沒有代價函數值(姿態調整時間)，且隨著節點數增加，CPU計算時間增加；高斯偽譜法產生規劃結果所需CPU計算時間隨著配點數的增加而增加，配點數為20時約為動力學RRT*算法初次得到可行軌跡所需時間的4倍。

表3 不同算法的CPU計算時間與代價函數值對比Table 3 Comparison of CPU calculation time and cost function values of different methods

4 結 論

1) 提出了兼顧自由漂浮空間機器人能量消耗和姿態調整時間的加權Bolza形式性能指標作為軌跡規劃的代價函數，增強了規劃的目的性和靈活性。

2) 對算法原有的模型線性化方法進行改進，針對性地采用偽線性化方法獲得FFSR的狀態空間模型，模型描述更加清晰、精確，運算更加簡便。提出了FFSR機械臂避障與機械手避障兩層次避障策略，提高碰撞檢測效率。

3) 使動力學RRT*算法具備了對多體系統的軌跡規劃能力，通過多次迭代的優化策略構建了無碰最優軌跡的逼近求解框架。仿真結果表明，該方法能夠以較快的速度生成可行的FFSR移動軌跡。