輪腿式火星探測機器人的多目標協同控制
孫筵龍,何俊,* , 邢琰
1.上海交通大學 機械與動力工程學院, 上海 200240 2.北京控制工程研究所, 北京 100190
火星環境對人們來說復雜而又未知,火星表面存在大量土壤松軟區域、陡坡及各種未知障礙物[1]。這些惡劣的環境對火星車的機械結構和控制系統都提出了新的挑戰和要求,眾多學者提出了多種火星車方案。美國先后開展了4次火星探測任務,發射的火星車均采用搖臂轉向架式懸架結構[2],該類型的火星車對地形具有良好的通過性;哈爾濱工業大學有關學者提出了一種輪步復合式移動系統構型,提高了火星車對復雜地形的通過性[3]。隨著火星探測任務的深入,為了進一步提升火星車對火星各種地形的適應性,眾多學者深入研究了火星車的主動調節能力,提出了多種輪腿主動懸架式機器人。加拿大研究人員研發了一種四輪腿機器人MHT[4],能夠實現對機器人車體姿態的主動調節;德國研究者設計了一種新一代的火星車SherpaTT,具有輪腿主動懸架結構,能夠主動適應復雜地形[5];中國的有關研究人員基于Stewart平臺開發了一款四輪腿機器人BITNAZA[6]。輪腿式機器人綜合了腿式機器人和輪式機器人的優點,該類機器人具有高機動性、適應環境強等特點,能夠實現對地外行星的大范圍巡視,具有跨越大障礙物的能力。輪腿式機器人除了具有輪式行進和腿式行進的步態外,還具有其獨特的多種步態形式,以此來適應復雜多變的環境,如:文獻[7]中基于腿部主動懸架的輪式行進步態,這種步態形式發揮了輪式行進的高機動性和腿部對環境的主動適應性;文獻[8]中的“狗刨”式步態,該步態在車輪陷入軟土時,能夠擺脫困境,避免下陷。具有輪腿式主動懸架結構的火星車,成為未來火星探測研究發展的趨勢。
探測機器人引入輪腿式主動懸架,提高了機器人對不規則地形的自適應能力和運動的穩定性,但同時也給控制帶來了新的挑戰。面對未知的地外天體環境,輪腿式機器人在行進中的穩定性難以保障,車體姿態、足端接觸力、車輪的驅動力都將影響其行進的穩定性,車體姿態、足端接觸力控制是保障輪腿機器人穩定行進的前提,可以避免車體不確定的振動,足端懸空、滑移及驅動力不足等問題。輪足車輪驅動力控制即過驅動問題也是輪足機器人穩定行進的研究重點。要實現輪腿機器人在不規則地形的穩定行進,多個控制的協同控制必不可少,這也帶來了新的控制問題和挑戰。本文主要研究輪腿機器人車體姿態、足端接觸力和車體重心高度的協調控制問題。德國研究者提出了利用車體姿態和足端力實現對車體姿態和足端力調整的控制方案,并在SherpaTT機器人上實施了控制方案,提高了SherpaTT機器人對地形的通過性及驅動力的穩定性[9];日本有關學者基于ZMP(Zero Morment Point)點對六輪腿機器人提出了一種車體姿態調整的控制方案,提高了六輪腿機器人運動的穩定性[10];日本研究者在Hydrover-II機器人上實施了車體重心加速度和車體姿態協同控制的控制方案[11]。
輪腿式機器人的多目標協同控制包括身體姿態、足端接觸力及穩定性控制3個方面。姿態對無固定基座機器人的運動能力有較大影響,姿態的不確定變化嚴重限制其運動能力。文獻[12]針對衛星的姿態控制問題,提出了基于機器學習的姿態控制算法;文獻[13]提出了基于PID和邏輯模糊的姿態控制策略;在文獻[14]中提出了基于卡爾曼濾波的自適應姿態控制算法;文獻[15]針對小型無人直升機姿態控制提出了基于增強學習的飛行控制算法。由于在深空探測任務中可以使用的CPU資源非常有限,一些在地面上實驗效果很好的智能控制算法并不能應用于火星車控制。因此,研究基于少量數據處理和簡單計算的姿態控制算法,是實現有限資源下火星車姿態跟隨控制的關鍵。
在執行火星探測任務時,火星車經常會在不規則的復雜路面上行走,火星車的足端接觸力會隨著地形隨機變化,這會使火星車足端受力不均,甚至會有車輪懸空的情況。火星車將會產生動力不足、側滑、輪子受損等問題。阻抗控制被廣泛應用于解決恒力跟蹤問題,能夠有效提高機器人在復雜環境運動中的魯棒性。文獻[16]提出了2種基于阻抗控制的自適應力跟蹤控制框架,并在一個七自由度機械臂上實現了力的跟蹤控制;文獻[17]采用基于模糊自適應阻抗控制,實現了高空幕墻安裝機器人末端接觸恒力控制;文獻[18]提出了一種非結構環境下基于自適應變阻抗的力跟蹤控制策略,實現了埃斯頓ER16機器人在非結構環境中的力跟蹤控制;文獻[19]提出了單神經元自適應 PID 的機器人恒力控制自適應算法,實現了KUKA 工業機器人的力跟蹤控制;文獻[20]針對機器臂捕獲空間未知物體,提出了魯棒自適應力跟蹤阻抗控制算法。針對火星車在執行探測任務時遇到由于足端接觸力受力不均而引起的車體驅動力不足、輪子易損和側滑等問題,提出了基于阻抗控制算法的機器人足端恒力接觸控制算法。
穩定性是輪腿式機器人順利執行任務的前提和基本要求。近年來眾多穩定性的評價指標被提出,如:文獻[21]提出的ZMP穩定性判據,ZMP點是機器人所受合力矩為零的點,若ZMP點位于機器人支撐多邊形內則機器人處于穩定狀態,反之亦然;文獻[22]詳細闡述了能量法判別機器人穩定性的原理;文獻[23]提出了力角法,即施加在底座上的合力和在低速假設下的傾覆軸法向之間的最小角度,來分析機器人的穩定性;文獻[24]提出了機器人三維空間內的穩定性判別,該判別法可應用于不規則的地形環境。對輪腿式機器人在不規則路面行走的穩定性進行研究,分析其ZMP點與其支撐凸面投影幾何中心的距離,驗證了多目標協同控制對提高機器人穩定性的有效性。
輪腿式火星探測機器人需要在復雜、未知的環境中自主行走,目前對火星表面環境信息的認知并不充分,缺乏土壤承載能力、密實度和地形、障礙物等數據,因而要求火星探測機器人對環境和地面有較強的自適應能力。此外火星探測機器人可以利用的CPU資源非常有限,因此需要研究簡單有效的控制算法,來保證輪腿式火星探測機器人對火星地形的自適應能力。本文建立了輪腿式火星探測機器人運動學模型,提出了輪腿式火星探測機器人的多目標協同控制器,包括:車體姿態控制器、腿部阻抗控制器和重心高度控制器,可實時調節腿長,并通過運動學反解模型獲得期望的關節角,實現了輪腿式火星探測機器人通過不規則地形時的車體姿態跟蹤控制、足端恒力接觸控制和重心最優高度控制,提高了輪腿式火星探測機器人對不規則地形的自適應性和運動的穩定性;在MATLAB/Simulink和UG中搭建了非結構環境下輪腿式機器人系統仿真模型,仿真結果驗證了多目標協同控制策略的有效性。
1 機器人運動學建模
輪腿式火星探測機器人由車體、4個完全相同的輪腿組成,輪子安裝在腿的末端,車體上裝有姿態傳感器IMU(Inertial Measurement Unit),4個 足端各有一個力傳感器,如圖1(a)所示。每條腿有轉向關節、側擺關節、髖關節、膝關節及車輪旋轉關節5個自由度,因此腿末端在三維空間中具有3個移動和一個轉動自由度,每個關節均為電機驅動的旋轉關節。腿部采用平行四邊形結構實現髖關節和膝關節的二自由度運動,將膝關節的驅動單元放在髖關節位置,這樣輪腿式火星探測機器人的重量集中于車體上,使腿部輕量化[25]。該結構提高了機器人的承載性能,減小了腿部運動的慣性。
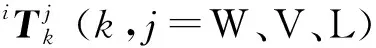
(1)
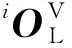
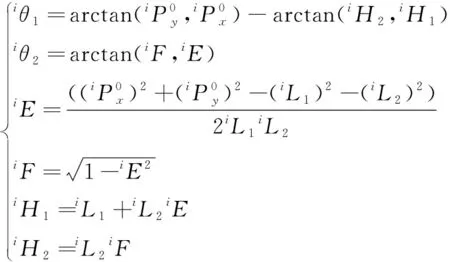
(2)

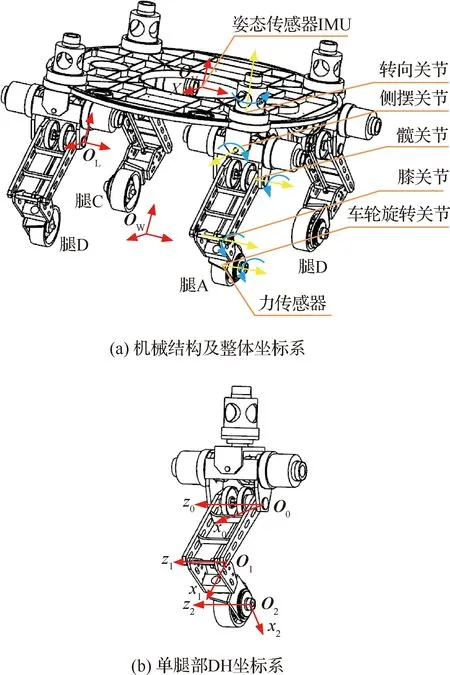
對輪腿式火星探測機器人的運動規劃需要統一在車體坐標系下進行,這樣有利于對輪腿式火星探測機器人系統進行整體控制,因此需進行如下運動學求解:
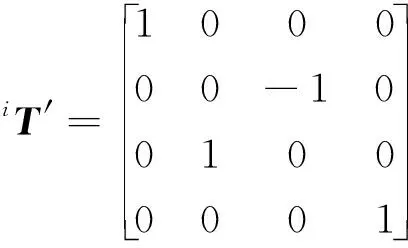
(3)
(4)
(5)
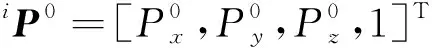
2 多目標協同控制建模
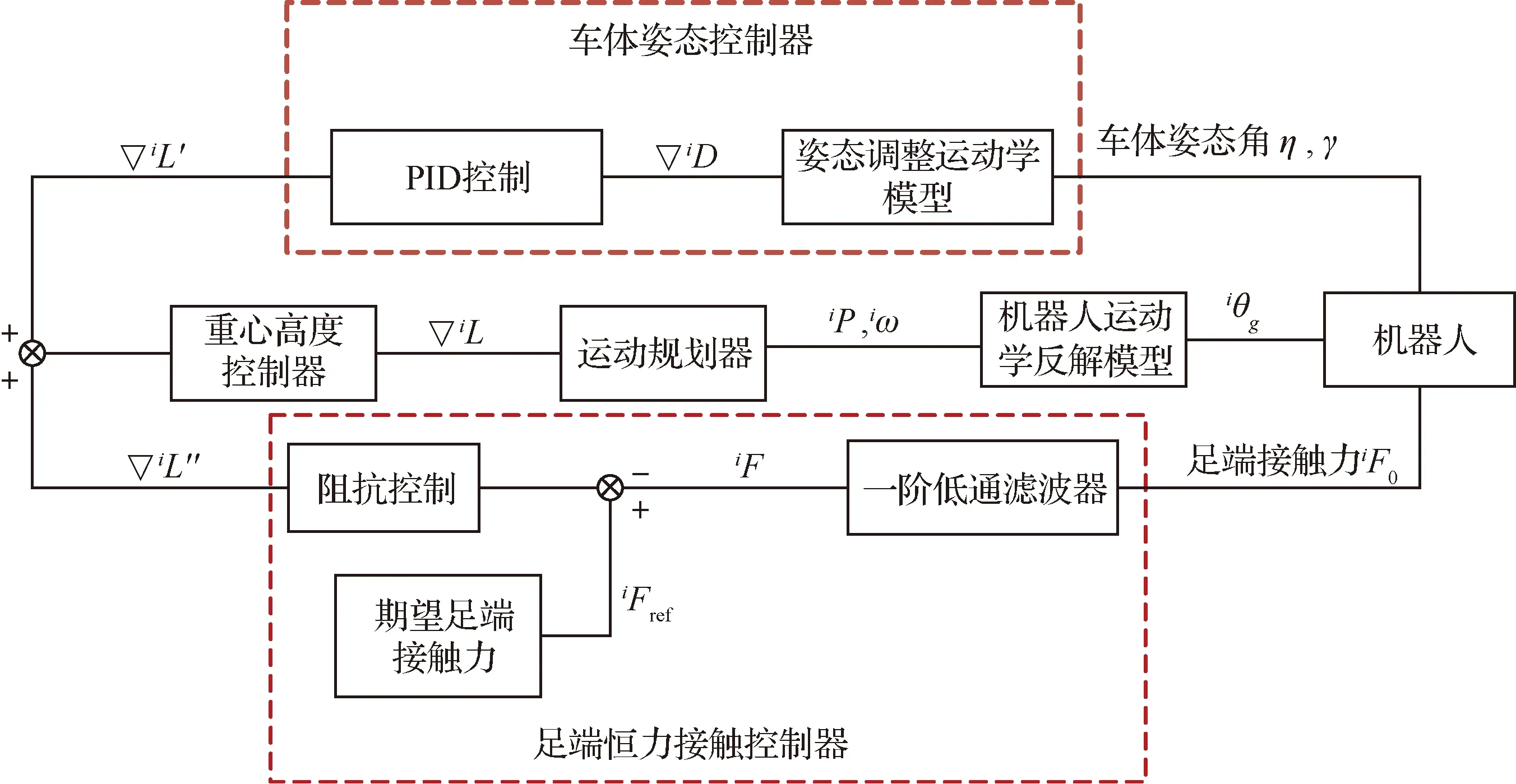
本部分詳細介紹了,輪腿式火星探測機器人在不規則地形中輪式行進時,多目標協同控制系統,包括: ① 身體姿態控制器,實現車體姿態的跟隨控制;② 足端恒力控制器,保證輪腿式火星探測機器人足端與火星表面的恒力接觸;③ 重心高度控制器,保障腿部運動空間的安全性。利用UG和MATLAB聯合仿真搭建了輪腿式火星探測機器人多目標協同控制仿真系統,如圖2所示。仿真實驗部分詳細介紹了仿真系統的搭建。
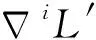
輪腿式火星探測機器人的車體姿態控制、足端接觸力控制和重心高度控制三者之間相互影響,存在耦合關系。姿態的變化及外界對足端的沖擊力都將引起足端接觸力的變化,此時車體姿態控制器和足端恒力控制器都將調整輪腿機器人的腿長來適應外界的變化。分析發現兩者對腿長的調整趨勢是一樣的,如圖3所示,車體姿態變化引起了足端接觸力變化,此時車體姿態控制器和足端恒力控制器都將調整腿B、C伸長、腿A、D壓縮,兩者呈現正相關性,此外當機器人處于無阻擾控制機器人狀態時此時車體姿態控制器無法發揮作用,足端恒力控制器將調整腿長實現足端恒力接觸,這也避免了單純的姿態控制引起的車體沿對角腿軸線翻滾的情況,起到了預測車體翻滾趨勢的作用。為增加控制系統的穩定性和抗干擾能力在車體姿態控制加入PID控制算法,足端恒力控制器中采用阻抗控制算法。同時車體姿態控制、足端接觸力控制引起了車體重心高度的變化,通過研究腿部的運動空間,形成了基于腿部危險系數的重心高度控制算法,其綜合考慮了車體姿態控制、足端接觸力控制引起的輪腿機器人腿部運動空間的變化,如圖3所示,重心高度的控制不會對車體姿態和足端接觸力產生影響。各控制算法在下文進行了詳細闡述。
2.1 姿態控制
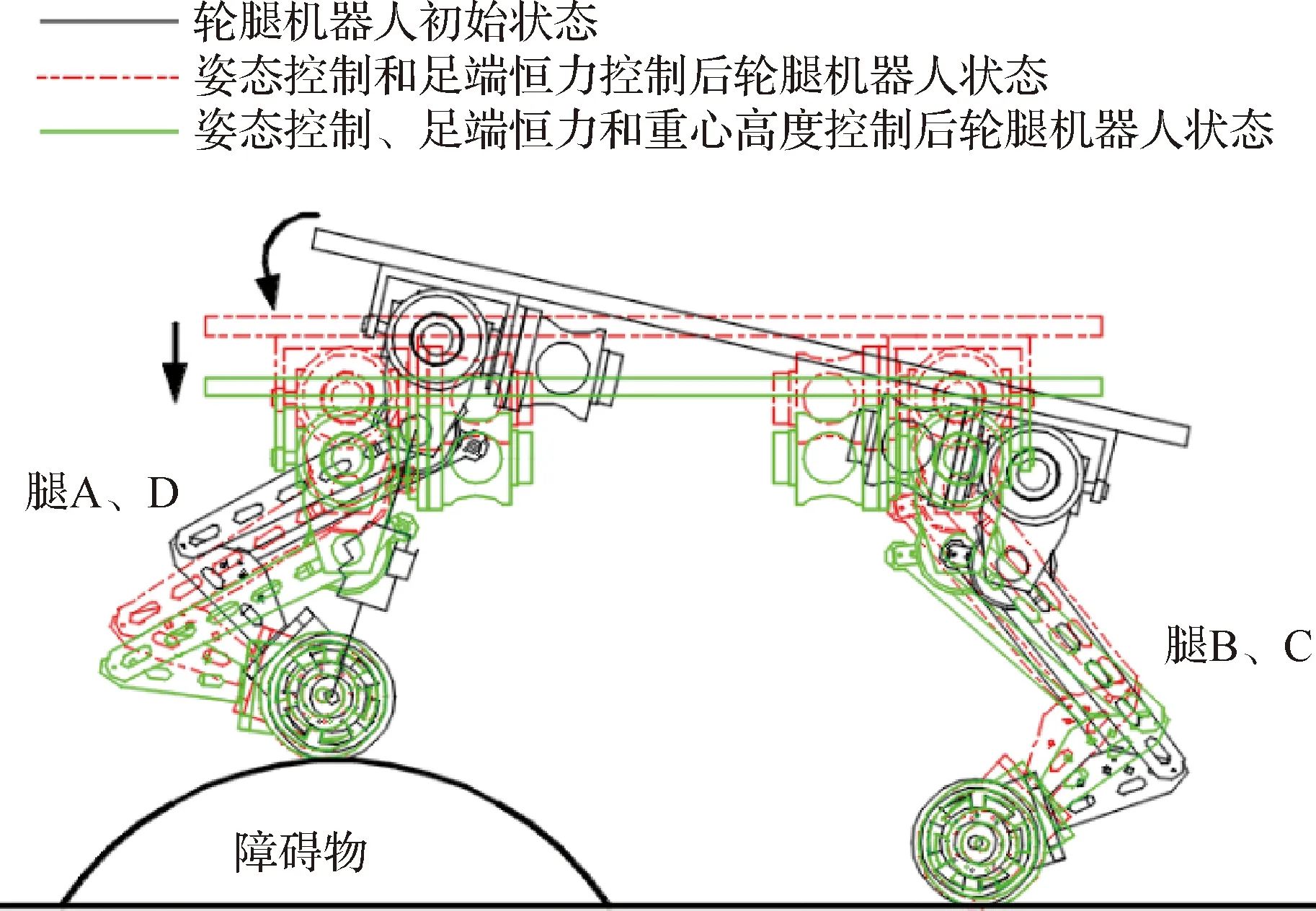
輪腿式火星探測機器人在不規則的復雜地形行進時,身體姿態總是隨著地形隨機變化。地形對車體姿態的影響嚴重限制了機器人的運動能力,甚至會出現機器人翻倒的危險,使機器人喪失執行任務的能力和損壞元器件。為了實現機器人姿態跟隨控制,提高機器人對地形的通過性,基于機器人在地形中所處的狀態,建立了姿態調整的運動學模型。車體俯仰角隨著地形發生變化時,車體的調整過程,如圖4所示。
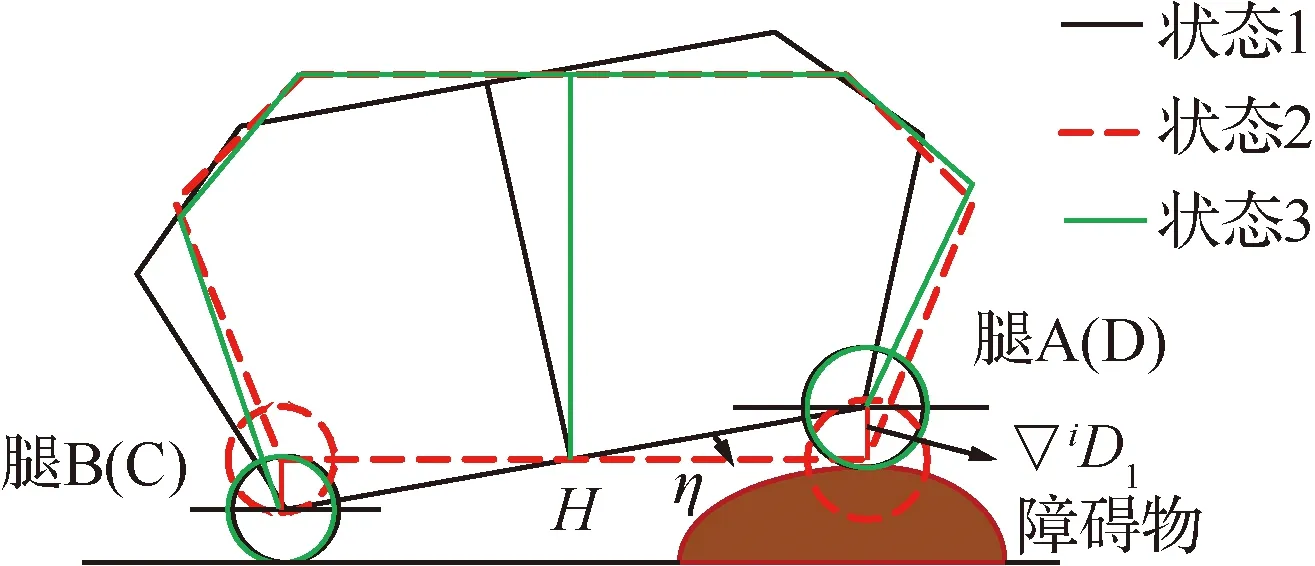
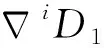
(6)
與上述分析過程相似,可以得到車體翻滾角γ發生變化時,進行姿態調整所需的理想腿長調整量為
(7)
綜上可得車體姿態角η、γ發生變化時腿長補償量為
(8)
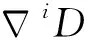
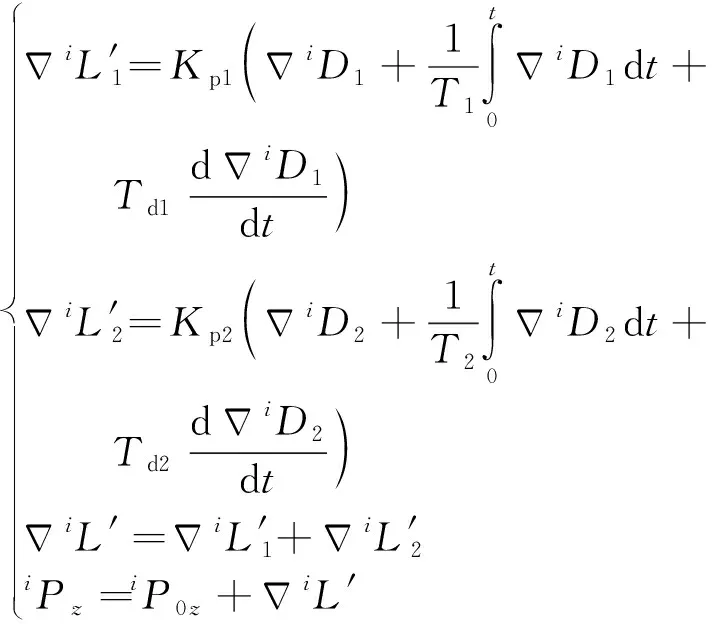
(9)
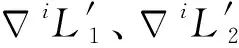
2.2 接觸恒力控制
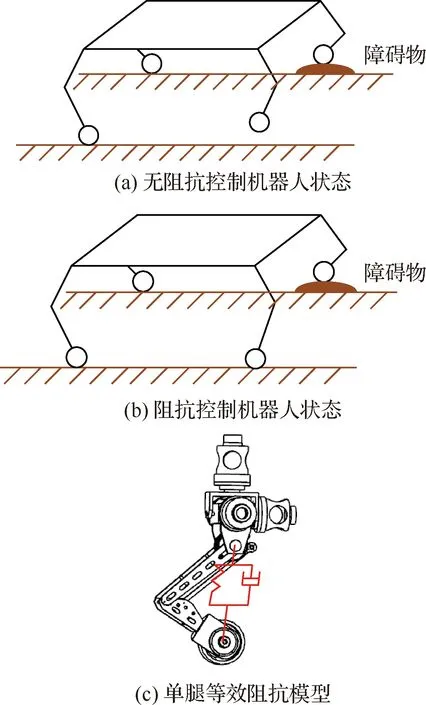
輪腿式火星探測機器人在平坦的火星地形上行進時,4個足端將與火星表面可靠接觸且足端重力方向接觸力為恒力。但輪腿式火星探測機器人在執行探測任務時必然會遇到不規則的復雜地形,這時足端接觸力將受力不均且會出現足端懸空的情況。圖5(a)中輪腿式火星探測機器人在不規則地形行進時,腿B、C在火星表面上,腿A在障礙物上,腿D處于懸空狀態,機器人因腿A、B、C形成的三角形支撐區域保持穩定。但這種足端受力不均甚至足端懸空情況的出現,會使機器人出現側滑,加速車輪損傷,驅動力不足等問題,嚴重影響了輪腿式火星探測機器人對地形的自適應能力和運動穩定性。利用阻抗控制算法實現輪腿式火星探測機器人由圖5(a)狀態調整為圖5(b) 狀態,此時腿D與火星表面接觸,實現了輪腿機器人足端與火星表面可靠接觸且足端重力方向接觸力iF0均勻分布。
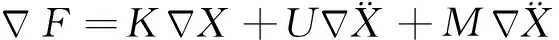
(10)
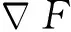
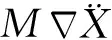
(11)
式(11)經拉普拉斯變換可得
(12)
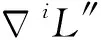
式(11)中需要獲得足端期望接觸力iFref和實際接觸力iF。足端實際接觸力iF由輪腿式火星探測機器人4個足端力傳感器測量獲得,但由力傳感其采集得到的力信號中夾雜著大量的高頻振蕩信號。對信號處理算法進行了研究,利用一階低通濾波算法,從原始力信號iF0中提取了可用力信號iF。
(13)
式中:fc為截止頻率。
足端期望力iFref應盡可能相近,假設輪腿式火星探測機器人低速行進,只受火星重力及足端接觸力的作用[9],對機器人進行整體靜力分析可得
(14)
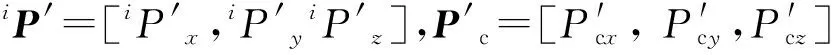
設
(15)
式(14)可寫為
(16)
式中:H+為偽逆矩陣,H+=HT(HHT)-1。
為計算方便,這里取平面μ過輪腿機器人重心COG,平面μ中坐標系O′由坐標系OV繞其X軸、Y軸分別旋轉γ、η角得到。因此P′c=[P′cx,P′cy,P′cz]=[0,0,0]并可由車體的當前姿態求解iP′=[iP′x,iP′y,iP′z]。
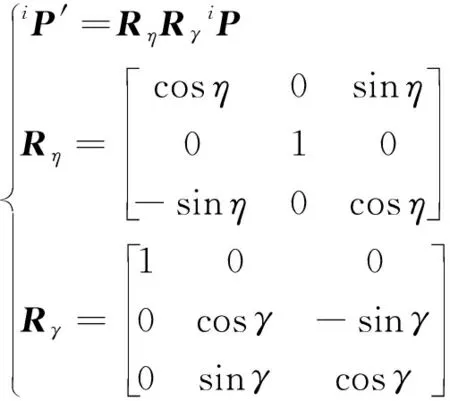
(17)
式中:Rη和Rγ分別為車體坐標系OV繞其X軸、Y軸分別旋轉γ、η角的旋轉矩陣。由此式(16) 得以求解。
2.3 重心高度控制
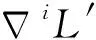
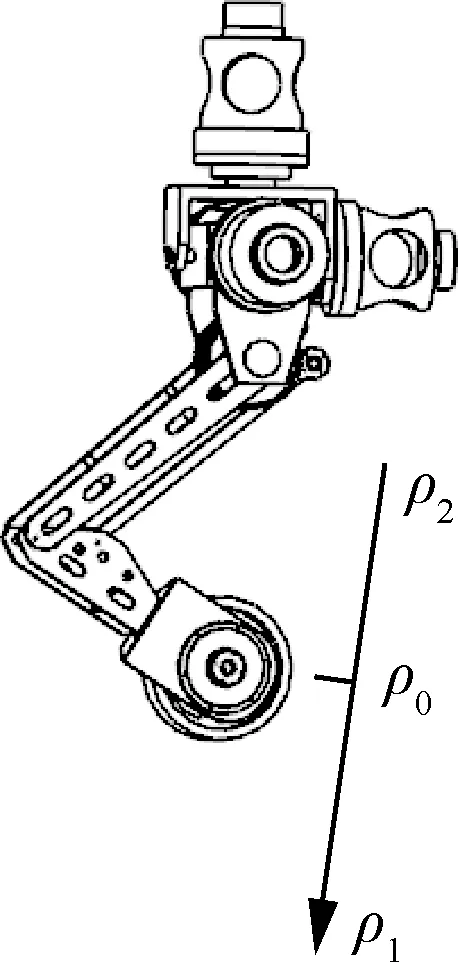
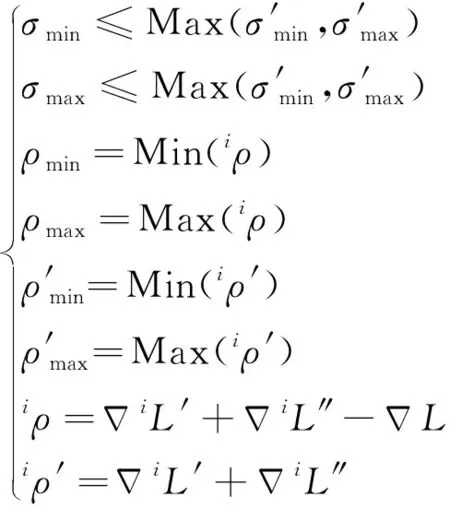
(18)
3 仿真驗證
3.1 仿真工況描述
為驗證多目標協同控制系統的有效性,在MATLAB/Simulink和UG中建立輪腿式火星探測機器人聯合仿真模型,實現了MATLAB/Simulink與UG間的信息交互。火星地形地貌的典型特征[1],如表1所示,在UG中建立輪腿式火星探測機器人機械系統和地形環境,如圖7所示,可以從中測量獲得機器人在輪式行進時足端在重力方向觸力iF0和車體姿態角η、γ。文獻[26]建立了MGM2011模型,能夠較為準確的估算出火星重力的分布,火星重力加速度約為3.6~3.8 m/s2,該模型在月球和地球上得到了驗證,本文選取火星重力加速度為gmars=3.7 m/s2。在MATLAB/Simulink中搭建多目標協同控制系統,實現車體姿態控制算法、足端恒力控制算法和重心高度控制算法。本部分進行了3次仿真實驗,分別為:① 無多目標協同控制;② 多目標協同控制;③ 多目標協同控制-無重心高度控制。并采集和分析了3次仿真實驗中的車體姿態角γ、η,足端接觸力iF,腿部危險系數σ和ZMP點等數據。
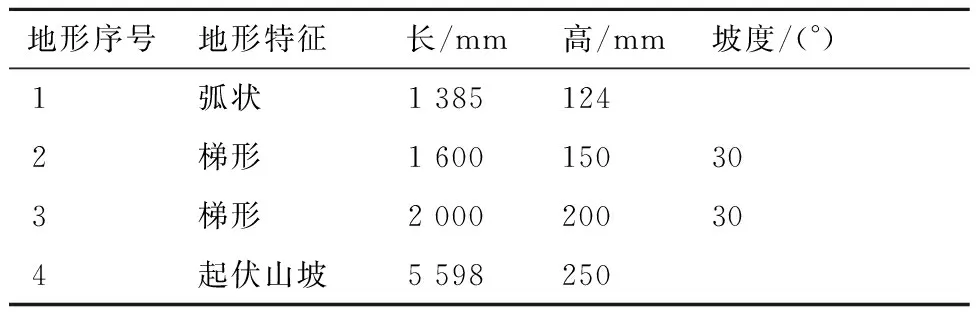
表1 仿真環境典型地形參數

仿真過程中,輪腿式火星探測機器人4個腿的布置方式為關于車體坐標系OV的X-Z平面和Y-Z平面對稱,因此4個足端期望接觸力為iFref=mgmars/4;車體理想的俯仰角η=0°,翻滾角γ=0°;運動規劃模塊給定輪速iω=4 rad/s(i=A, B, C, D),初始足端位置iP0;輪腿式火星探
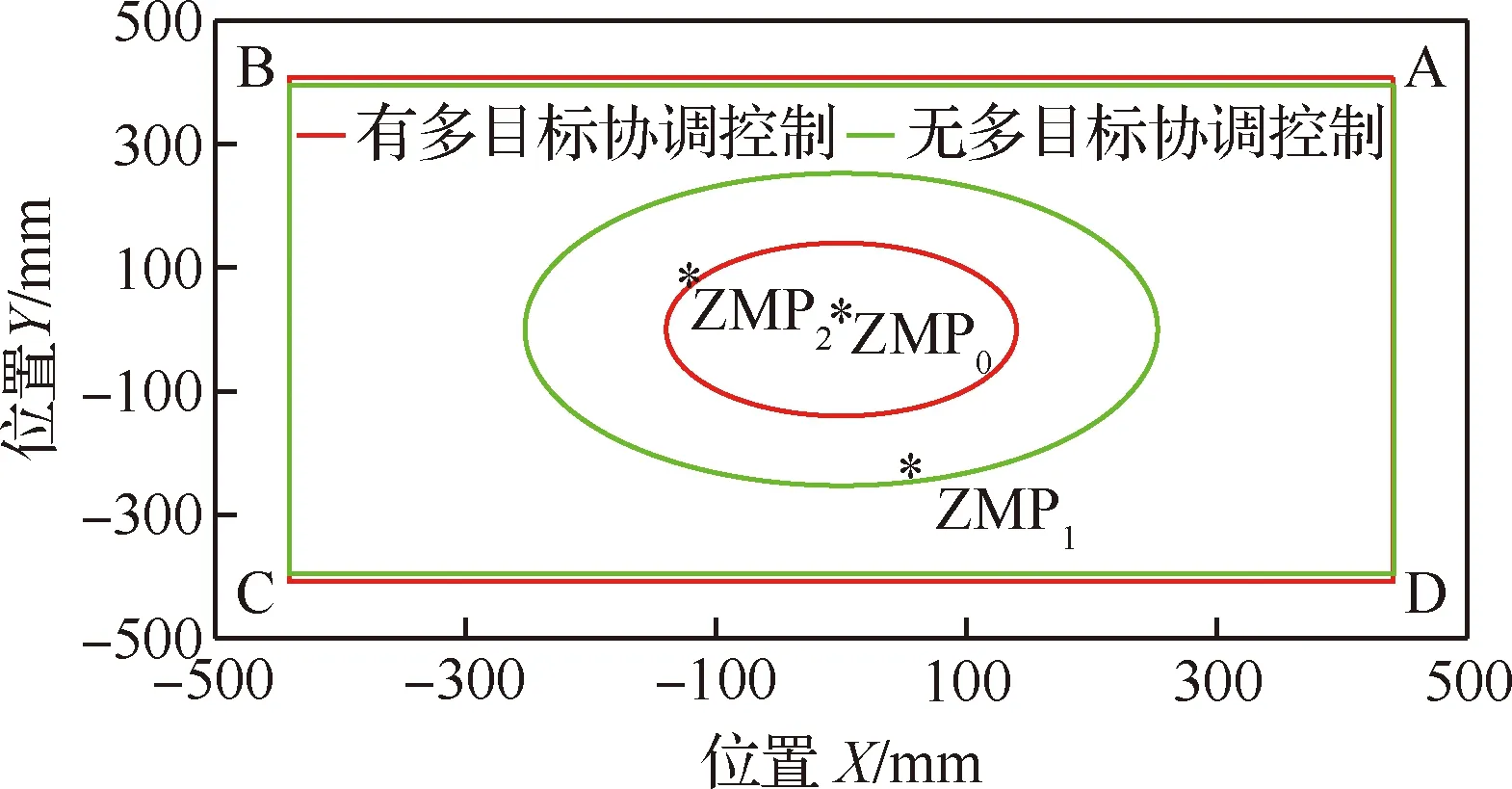
測機器人依次通過障礙物1、障礙物2、障礙物3、障礙物4,仿真持續時間為55 s。為分析輪腿式火星探測機器人在運動過程中的穩定性,將4個足端點投影到平面μ中,4個足端投影點形成的多邊形區域,足端點記為A、B、C、D,面積記為S。輪腿式火星探測機器人在平坦的火星地形上行進時,其ZMP點記為ZMP0=(0,0),4個足端投影點形成的多邊形區域面積記為S0。在坐標系O′中計算輪腿式火星探測機器人ZMP點:
(19)
(20)
(21)
式中:(Xzmp_t,Yzmp_t)為t時刻輪腿式火星探測機器人ZMP點坐標;dt為t時刻輪腿式火星探測機器人ZMP點到ZMP0的距離。
3.2 仿真結果分析
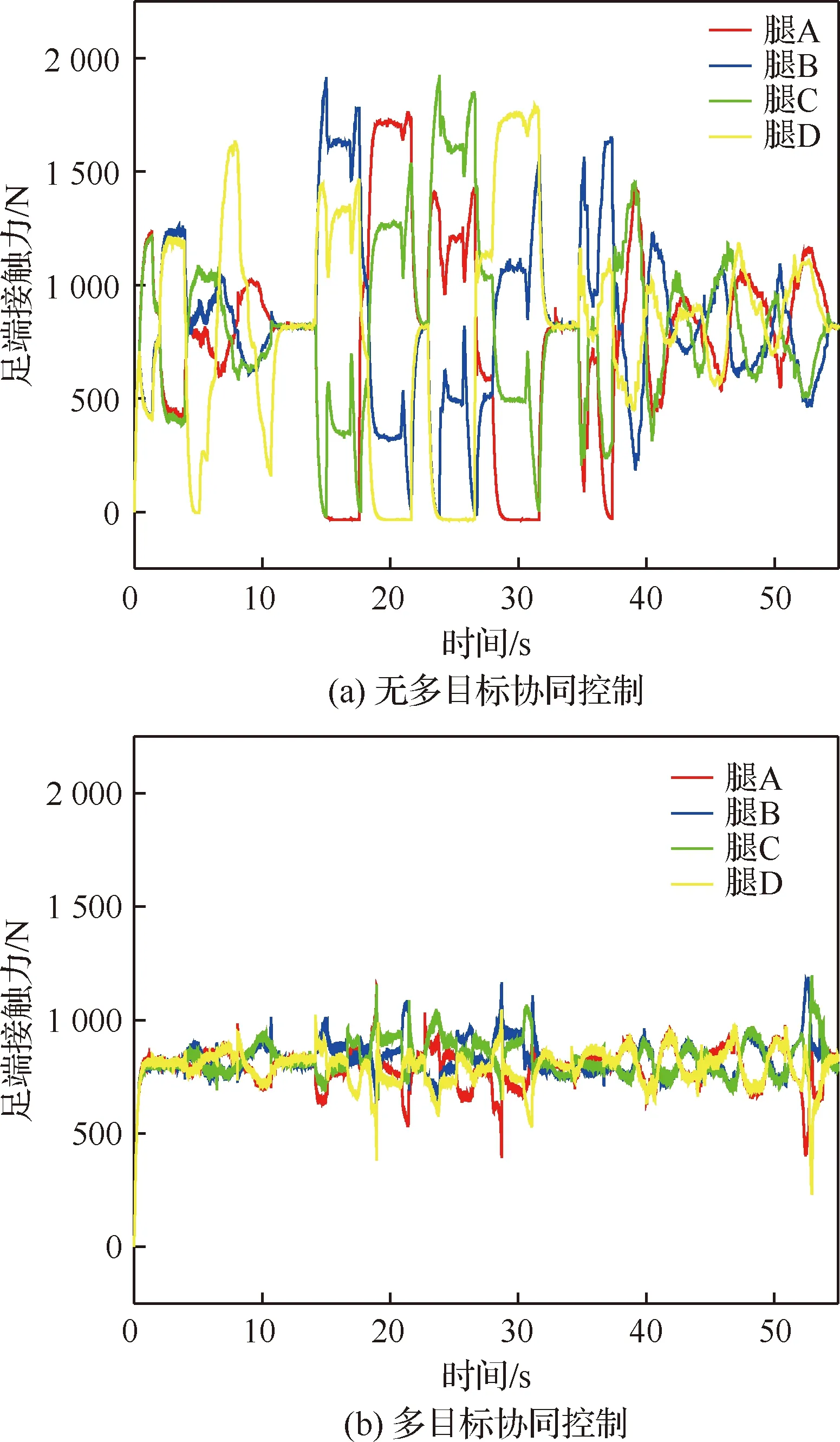
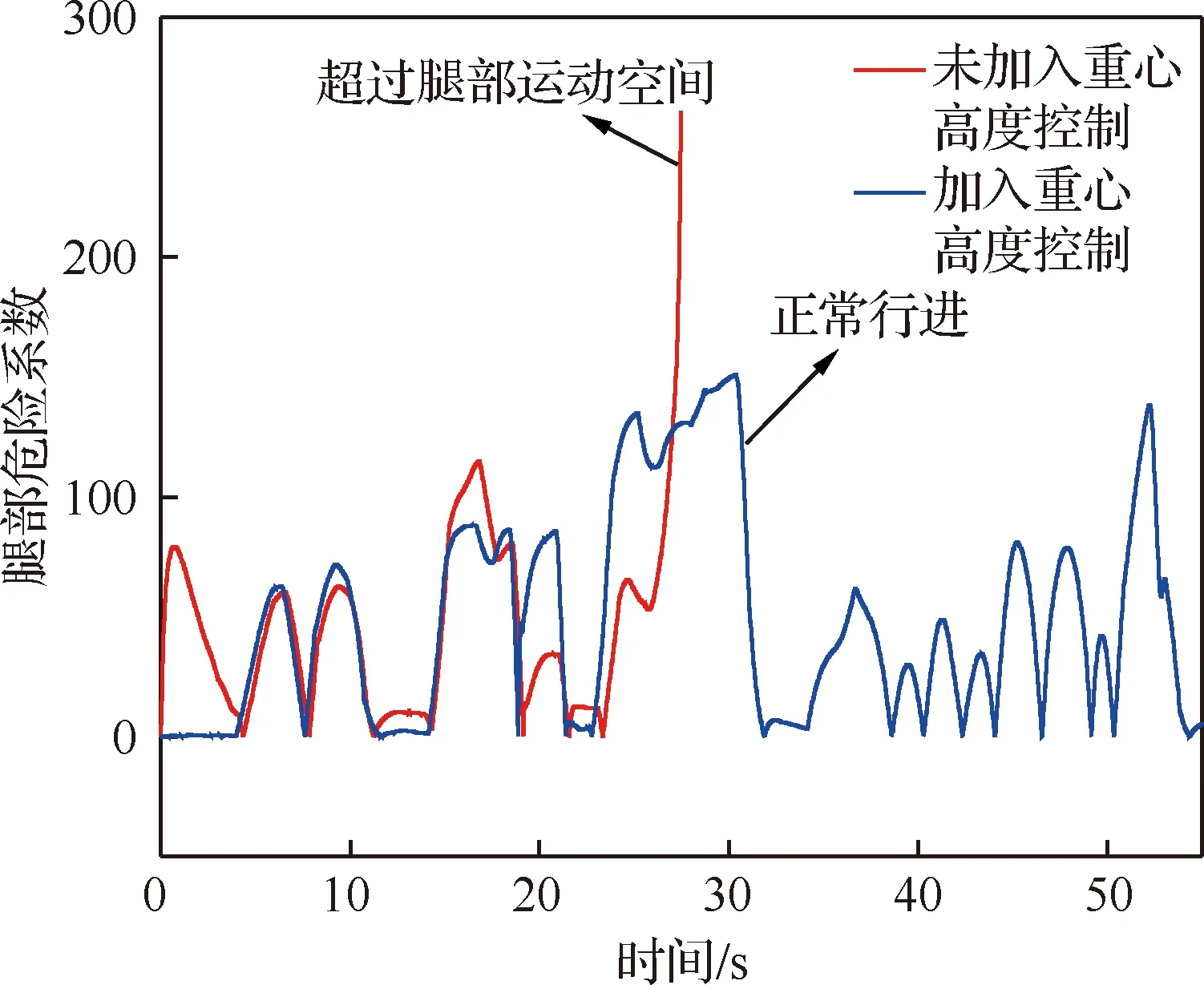
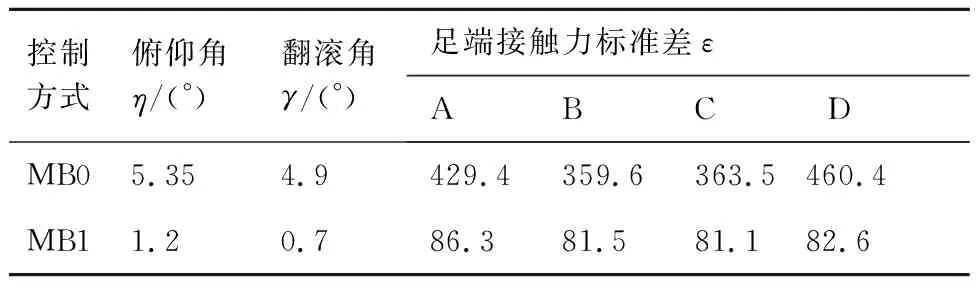
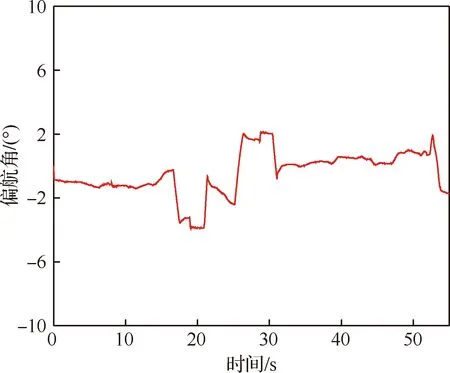
輪腿式火星探測機器人車體姿態角η和γ的變化曲線如圖8所示,足端接觸力iF的變化曲線如圖9所示。從實驗結果可以看出多目標協同控制有效改善了車體姿態角的大幅度變化和足端接觸力iF較大的分布不均等問題,使得車體姿態角η和γ分別在-3.78°~+3.48°、-3.66°~+2.47°范圍內小幅度波動,各足端接觸力iF在500~1 000 N中小幅度變化,由此可得多目標協同控制實現了車體姿態的跟隨控制,足端接觸力的恒力控制,提高了輪腿式火星探測機器人在不規則地形中的自適應能力。重心高度控制減小了腿部運動危險系數,27 s無重心高度控制時輪腿機器人由于D腿腿部危險系數σ過大,使得機器人停止運動,而多目標協同控制有效避免了該問題,使輪腿機器人正常行進,如圖10所示,此外在0~4 s重心高度控制,消除了足端恒力控制器中一階低通濾波器的延遲特性引起的腿部危險系數σ的變化,由此可得重心高度控制保障了輪腿機器人腿部運動的安全性,提高了其對復雜地形的自適應能力。在無多目標協同控制和多目標協同控制中,面積S最小值時,分別記足端點為A′、B′、C′、D′和A″、B″、C″、D″,面積S為S′和S″;dt最大時,分別記dt為dt1和dt2,ZMP點為ZMP1和ZMP2,此時以坐標原點O′為圓心dt1和dt2分別為半徑作圓1與圓2;因此輪腿式火星探測機器人在運動過程中其ZMP點分別在圓1和圓2中變化,如圖11所示。經計算S′=0.96S0,dt1=252.82 mm,S″=0.99S0>S′,dt2=139.97 mm 試驗結果的誤差分析主要分為兩類:① 針對仿真結果的誤差分析;② 針對仿真與實際工況的誤差分析。從3.2節中的仿真結果可知實施多目標協同控制后車體姿態角和足端接觸力的峰值誤差減小了約4倍,車體姿態角和足端接觸力的標準差為 (22) 表2中MB0表示無多目標協同控制,MB1表示實施多目標協同控制。如表2所示,車體姿態角、足端接觸力變化的波動大小都降低了約4倍。同時在控制過程中理論上車體的偏航角將保持為零,從圖12可以看到偏航角發生了變化,但變化很小在-4°~2°范圍內小幅波動,分析發現這主要是由于在控制過程中沒有根據車輪與地形的接觸狀態對車輪運動加以控制,常用的控制方法有速度控制和力矩控制,關于車輪的運動控制問題不在本文的研究范圍內,這里不在進行詳述,偏航角較小的誤差不會對多目標協同控制算法有效性的驗證產生影響。綜上可得多目標協同控制算法實施后輪腿機器人的車體姿態和足端接觸力仍會產生誤差,但誤差較小,車體姿態角和足端接觸力的峰值誤差及波動大小,均有明顯改善,所以仿真結果驗證了多目標協同控制算法的有效性。 表2 車體姿態角和足端接觸力標準差 仿真環境與實際工況存在一定的差距,主要的誤差來源于運動學模型的準確性、外界不確定噪聲對傳感器信號的干擾、實際工況與典型地形的差別。在實物模型中,由于加工精度、機械裝配等會給運動學模型帶來一定的誤差,這種誤差可以通過重復進行試驗,求取平均值的方法提高運動學模型的準確性[7];針對外界不確定噪聲帶來的傳感器測量誤差,可以使用抗干擾強的傳感器和濾波算法,對于傳感器和濾波算法的研究這里不在進行闡述;本文通過仿真實驗驗證了多目標協同控制策略對輪腿機器人在典型工況中運動的有效性,在實際的火星地形中地面承載力變化的隨機性較大,但多目標協同控制算法具有一定的魯棒性,并能充分發揮輪腿式機器人主動懸架彈性系數與剛度系數可調的優點,通過實時調節阻抗參數與PID參數來適應各種隨機干擾,關于參數的實時調節不在本文的研究范圍內,未來將對其進行深入研究。 從以上實驗數據分析中可以看到盡管仿真結果存在微小誤差且仿真環境與實際工況有所差距,但多目標協同控制算法的有效性仍得到了驗證,該控制算法實現了車體姿態跟隨控制和足端恒力接觸控制,保障了輪腿式機器人腿部運動空間的安全性,提高了輪腿探測機器人對不規則地形的自適應能力和運動的穩定性。 1) 提出了一種基于車體姿態、足端接觸力及重心高度的多目標協同控制策略,為輪足機器人在非結構環境下移動控制提供了基本依據。 2) 利用UG和MATLAB進行聯合仿真,并對結果進行了誤差分析驗證了多目標協同控制策略的有效性,車體姿態角和足端接觸力峰值誤差均減小了約4倍且車體姿態角和足端接觸力波動大小也減小了約4倍。 3) 未來將對輪腿機器人在未知環境中的全地形運動控制進行研究,多目標協同控制器中PID參數及阻抗參數的在線辨識及輪腿機器人過驅動問題將是未來研究的重點。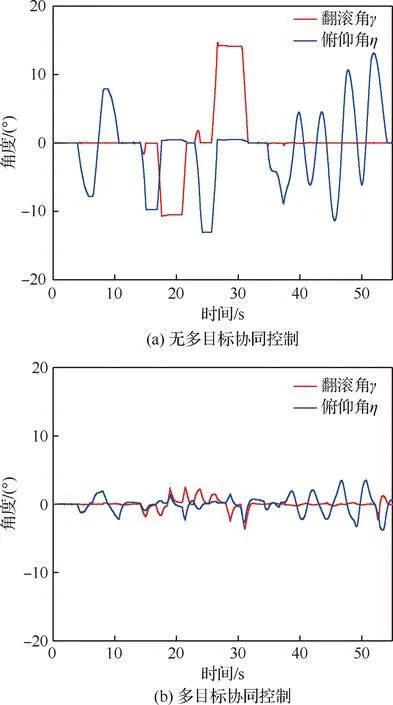
3.3 誤差分析
4 結 論

