CT 系統參數標定及成像研究
陳 浩 江子涵
(武漢大學,湖北 武漢430000)
1 文獻綜述
由于CT 系統對樣品破壞很小,故廣泛應用于醫療領域,自2013 年開始,對CT 系統的相關研究比較多,相關文獻發表量年度趨勢如圖1。
如圖可以看出,在2018 年達到頂峰,雖然之后在回落,但2020 年后也有上升態勢。縱觀國內相關研究文獻,計算角度的方法有的是采用尋找特殊點的方式,如找臨界狀態,或采用數據擬合得到角度等等。擬合往往計算量較大,當數據量比較大時得到結果較為困難或者對設備要求較高。因此,本文提出可以通過解析幾何的角度來解決角度的計算,可以在一定程度上減少計算量,提高精確度。
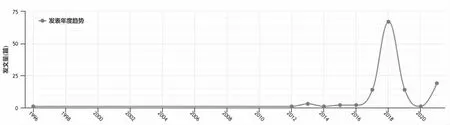
圖1 發表年度趨勢圖
2 系統參數標定
一般標定方式為將模板固定后,整個發射- 接收系統逆時針旋轉180 次,得到180 組接收信息數據,將第i 組數據記為xi,由于溫度、氣壓、空氣質量等因素或模板本身有缺損,得到的數據有可能產生誤差點,會對結果造成損害。因此,在處理前應該找出誤差點并作相應處理。誤差點可以通過拉依達準則來判斷,操作方式如下:

其中,xij表示第i 組數據中第j 個探測器單元的數值。當某個值不滿足以下拉依達準則:

表明這個點(xij)是偏差較大的點,應去掉或重新取值。
由于模板較為規整,可以找到最長截面和最短截面,而這兩種情況往往對應著接收信息最多和最少的兩組數據,進而由模板的數據來推算探測器單元間的距離。本文以圖2 所示的模板具體推導參數標定過程。
首先,建立平面直角坐標系,如圖3。
由圖3 可知,當X 射線方向平行于橢圓短軸時,獲取信息最多,可以得到如下表達式:
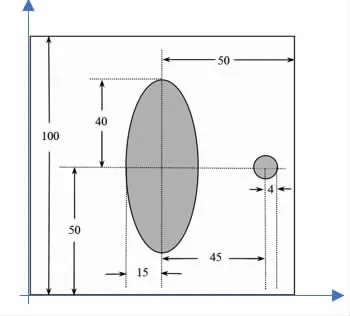
圖2 模板參數形狀示意圖
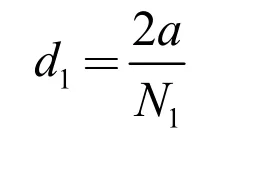
其中,N1是接收到信息的探測器單元數量,a 是橢圓長軸長度,d1是計算出來的探測器單元間的距離。類似地,對于X 射線平行于橢圓長軸的情況,同樣可以得到下面的表達式:
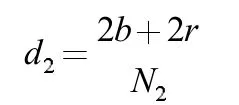
其中,b 為短軸長度,r 為圓的半徑,N2為接收到信息的探測器單元數量,d2是計算出來的探測器單元間的距離。由于測算誤差,d1和d2往往不相等,故可以采用取多次測量平均值的方式減少誤差,并計算出最后結果記為d。根據圖中數據可以計算得到d 為0.27709mm。由于從垂直于短軸到垂直于長軸旋轉了90°,那么旋轉中心點可以由這兩次X 射線照射中的探測器中心點的位置來確定(如圖4)。
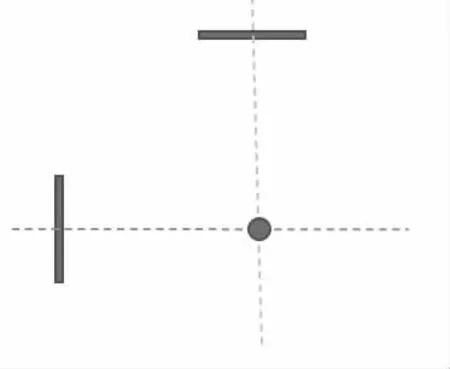
圖4

情形1:
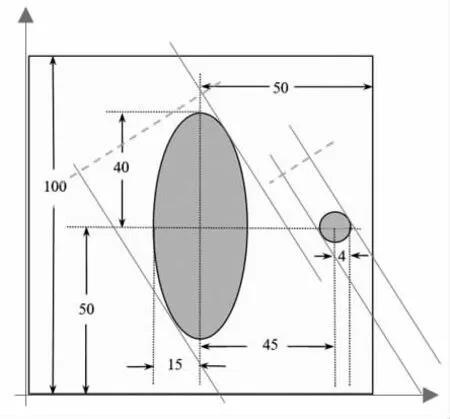
圖5
情形2:

圖6
對于情形1,設X 射線與水平軸的正半軸的夾角為θ,由于

3 基于Radon 變換的成像研究
函數f(x,y)的Radon 變換為:

4 結論
本文從解析幾何的角度考慮CT 系統的參數標定,基于Radon 變化完成對圖像重構的梳理,通過適當例子給出解決實際問題的方案。本文采用的解析幾何視角可以降低計算量,有助于提高生產效率。但是,在計算旋轉中心時,沒有利用到所有數據,誤差較大,這也是下一步工作的重點。

