冪律流體在多孔介質中球向滲流的分形模型

王世芳,吳 濤,蘇 怡

(1.湖北第二師范學院 理論物理研究所， 武漢 430205;2.武漢工程大學 光學信息與模式識別湖北省重點實驗室,武漢 430205)

1 引言

自20世紀60年代以來，在油田開發過程中越來越多的使用聚合物溶液、泡沫液和乳狀液等非牛頓流體作為驅油劑，因此研究非牛頓流體的滲流規律具用重要的現實意義。非牛頓流體的顯著特征是流量和壓力梯度不滿足線性關系。目前，諸多文獻研究了各種流體在多孔介質中的傳熱傳質特性，取得了較大的研究進展[1]-[6]。文獻[4]研究了冪律型流體在多孔介質作平面平行流的滲透率分形模型，得到了冪律流體有效滲透率隨冪律指數n的增加而增加的結論。文獻[6]研究了冪律流體在樹狀分叉網絡中的有效滲透率和相對滲透率的解析表達式。盡管這些研究結果有助于人們理解冪律流體在多孔介質中的流動機理，但是冪律流體在多孔介質中作球向流動的研究鮮有報道。

2 冪律流體在多孔介質中球向滲流的滲透率分形模型

球向滲流模型假設毛細管沿球徑向分布，該模型是石油開采中的一個重要模型。一般在沒有完全射開的油層開采時，球向滲流模型更符合實

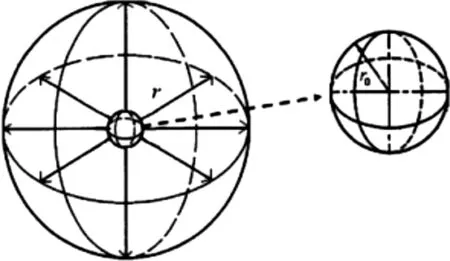
圖1 多孔介質中冪律流體球向滲流的示意圖

際情況[7]。三維的球向滲流廣泛應用于油、水、氣等儲集層，流體從井筒外部向滲流中心(即井筒中心)流動，其中r為滲流區域的半徑，r0為井筒半徑，圖1為多孔介質中冪律流體球向滲流的示意圖。

假定多孔介質的孔隙大小分布滿足分形分布，在一個多孔介質代表性單元體內，孔隙直徑大于或等于λ的累計孔隙數目可以表示為[8]：

(1)

對上式微分，于是得到：

dN=Dfλmaxλ-(Di+1)dλ

(2)

其中Df與λmax分別代表孔隙面積分形維數及最大孔隙直徑。

多孔介質的孔隙總面積可以寫成；

(3)

由孔隙率的定義得一個代表性單元的總橫截面積為：

(4)

其中代表性單元體面孔隙率φ與分形維數Df的關系滿足下列關系式[2]：

(5)

其中dE為歐幾里得空間維度數，在二維歐氏空間dE=2，在三維歐氏空間dE=3，下面我們推導多孔介質中冪律流體球向滲流的滲透率。

多孔介質的毛細管一般是彎曲的，毛細管的實際長度可表示為：

Lt=rDTλ1-DT

(6)

迂曲度分形維數Dr代表了毛細管的彎曲程度，其值越大代表毛細管越彎曲。

冪律流體流過單根彎曲毛細管的流量為：

(7)

通過積分得到冪律流體流過球形多孔介質某個截面的總流量為:

(8)

(9)

則冪律流體流過半徑為r的球形橫截面的平均流速為：

(10)

令式(10)中，上式就可以表示為牛頓流體在半徑為r處的平均流速：

(11)

方程(11)與苗同軍[21]模型結果一致，從而說明了本模型的正確性。

接下來我們要推導冪律流體的視粘度μa。冪律流體在毛細管管壁處所受的剪切應力τw與壓強梯度滿足下面關系式：

(12)

聯立公式(2)和(12)，推導出總剪切應力為：

(13)

根據冪律流體的視粘度定義為：

(14)

冪律流體的本構方程為：

(15)

根據式(13)(14)和(15)，推導出冪律流體的視粘度為：

(16)

冪律流體滲流滿足的廣義達西定律為[4]：

(17)

根據(11)(16)(17)從而推導出冪律流體在半徑r處球形橫截面的有效滲透率公式為：

(18)

如果n=1，上式(18)可以簡化為：

(19)

上式(19)表示多孔介質中牛頓流體在離球中心r處有效球向滲透率，此結論與苗同軍[21]研究的結論一致；式(18)表示在多孔介質中冪律流體球向滲流時的有效滲透率分形表達式。式(18)中包含分形維數DP、Dr，最大孔隙直徑λmax，最小孔隙直徑λmin及半徑r，沒有任何經驗常數，每一個物理量都有意義。所以式(18)反映了多孔介質中冪律流體球向滲流的有效滲透率的物理機理。當r=r0時，式(18)可以寫為

(20)

式(20)表示冪律流體在球形井筒壁處的有效滲透率，為了得到歸一化滲透率，用式(18)除以式(20)，得到冪律流體球向流動時無量綱滲透率：

(21)

方程(21)反映了冪律流體無量綱球向滲透率只取決于迂曲度分形維數DT、井筒的半徑r0和滲流半徑r，與冪指數n無關。此結果與文獻[20]研究的結果形式相同，該表達式也說明了無量綱滲透率與坐標系的選擇無關，僅取決于多孔介質的微結構參數和滲流半徑及井筒半徑。

3 結果分析

為了檢驗模型的正確性，我們將得到的無量綱滲透率模型(式21)與Chang和Yorttsos[9]提出的滲透率模型作比較：

(22)

其中θ是分形網絡的譜指數，是無量綱參數，一般是由分形多孔介質的微結構參數來確定，一般由蒙特卡洛模擬方法確定。

方程(22)也可表示為無量綱滲透率：

(23)

圖2 本模型(式21)與Chang and Yortsos’s模型Eq.(23)的比較，賦值參數如下：DT=1.7，φ=0.4，θ=1，DP=1.5。對于大多數多孔介質來說，孔隙率一般在0.1～0.5之間，本文孔隙率φ=0.4。從圖2可以看出：滲流半徑r越大，無量綱球向滲透率越小，當r>r0時，無量綱球向滲透率趨近于零。這是因為半徑r越大，球形橫截面上毛細管的數目越少，從而導致無量綱滲透率越小，這和現實情況相吻合。從圖2中也可以看出我們的模型與已有的Chang and Yortsos模型吻合的非常好，這說明我們的模型是正確的。

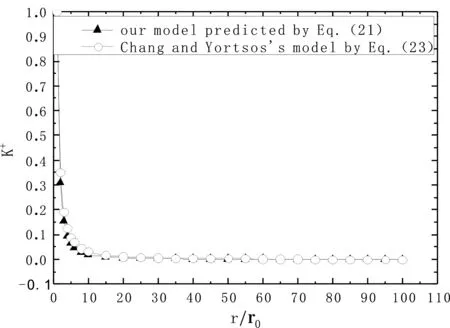
圖2 顯示了冪律流體無量綱球向滲透率隨徑向半徑比r/r0的變化關系

圖3顯示了球向有效滲透率(式18)和迂曲度分形維數DT的關系，所用參數賦值如下：r0=0.1m，r=100m，n=1.1。我們發現冪律流體球向有效滲透率隨迂曲度分形維數的增大而變小。這是因為迂曲度分形維數越大，說明冪律流體流動路徑越彎曲，冪律流體所受的流動阻力越大，導致滲透率越小，這與實際情況相符。另外，還可以看出孔隙率越大，冪律流體球向有效滲透率越大。這是因為孔隙率越大，流體流動越容易，滲透率越高，這也與實際情況相符。

圖4顯示了有效球向滲透率隨冪指數的變化關系圖，所用參數賦值如下：r0=0.1m，r=10m，DT=1.2。從圖4中我們發現冪律流體的冪指數n越大，球向有效滲透率越大。這是因為冪律流體的冪指數越大，表明非牛頓流體特征越弱，從而導致滲透率越大。

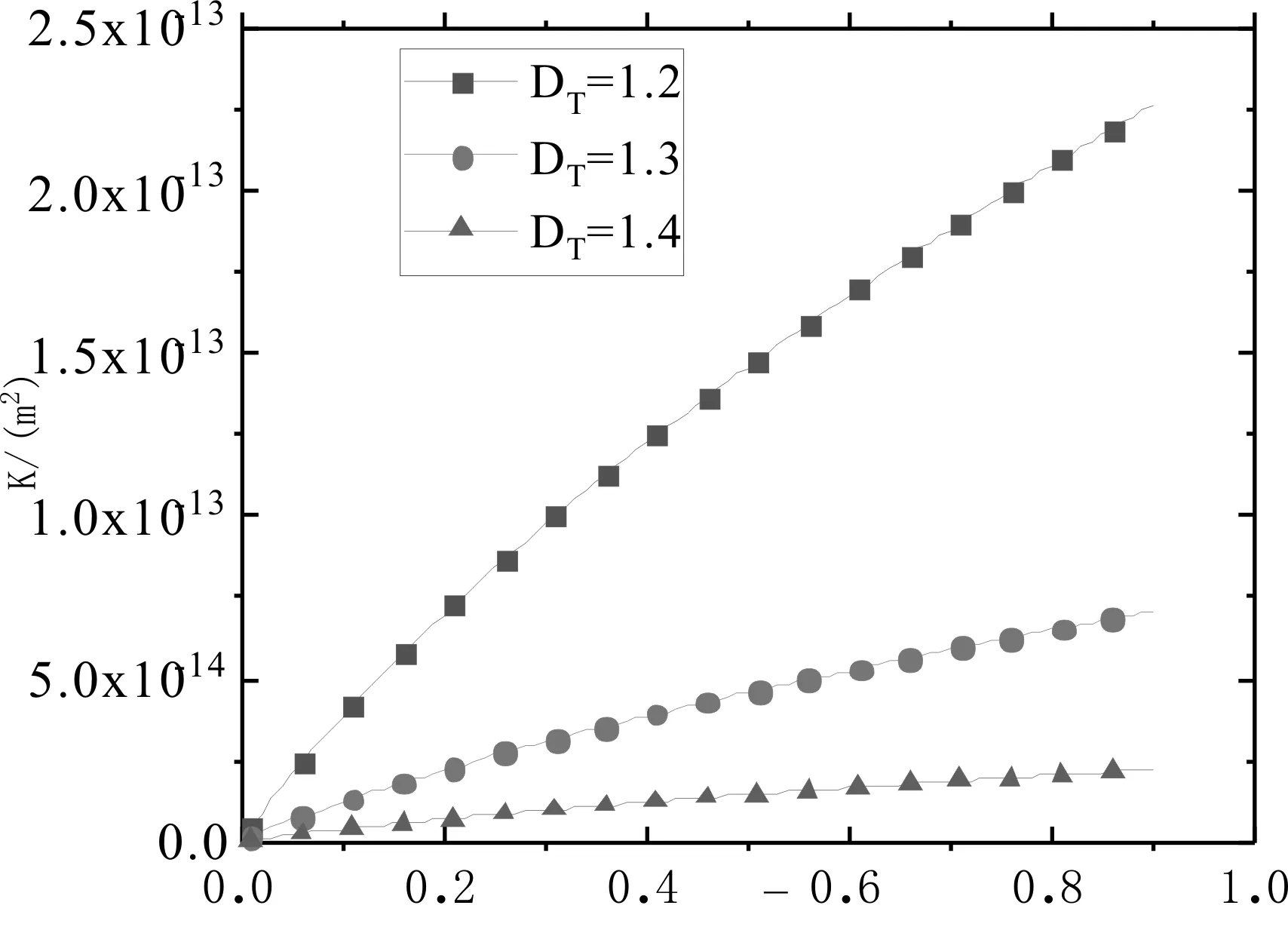
圖3 冪律流體球向滲透率隨孔隙率及迂曲度分形維數的變化關系

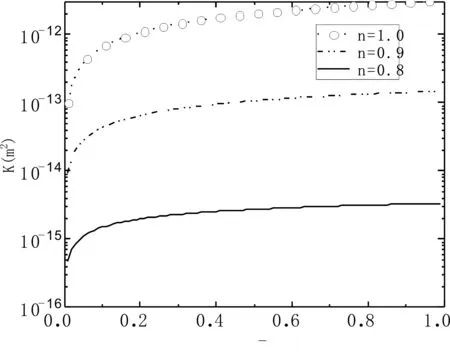
圖4 冪律流體球向有效滲透率隨冪指數的變化關系圖

4 結論

本文根據冪律流體滿足的達西定律和多孔介質的分形幾何理論，推導出了多孔介質中冪律流體球向滲流時的有效滲透率，該有效滲透率方程與多孔介質微結構參數和冪律流體的特性有關，每個物理量物理含義明確。