工藝參數對防護梁繞彎成形的壁厚影響研究

丁立波，梁田，李明杰，梁繼才

工藝參數對防護梁繞彎成形的壁厚影響研究

丁立波1，梁田2，李明杰1，梁繼才2

（1. 白城職業技術學院，吉林 白城 137000；2. 吉林大學 材料科學與工程學院，長春 130000）

探究“日”字形截面型材繞彎成商用車防護梁時工藝參數對型材壁厚的影響，以提高防護梁制件的產品質量。基于有限元仿真分析，利用正交試驗設計模擬出不同工藝參數配比下型材的成形過程，并對型材彎曲段外側壁厚減薄量和內側壁厚增厚量進行極差分析。工藝參數中彎曲半徑和芯模的芯頭個數對外側減薄率和內側增厚率影響極大，其余參數相對影響較小。依據正交試驗結果并綜合分析，最終確立了較好的防護梁繞彎成形方案，并通過試驗驗證了模擬結果的有效性。證明了選擇合適的工藝參數配比可以顯著減輕型材的壁厚變化，從而極大提高防護梁制件的產品質量。

繞彎成形；“日”字形截面型材；正交試驗；有限元仿真；工藝參數

防護梁是汽車前保險杠的重要組成部分，是在發生碰撞事故時，與車或行人最先接觸的部位[1—2]。為最大程度地減輕人員傷亡和財產損失，必須保證防護梁的防撞性能，而這也是一項重要的研究內容。文中以“日”字形截面高強鋼型材[3]為初始型材，利用繞彎工藝將型材兩端彎曲30°，最后成形制得防護梁。繞彎方法成本低，效果好。高強鋼的應用也滿足了汽車輕量化的要求[4—5]，但在彎曲過程中由于切向拉應力的作用使外側壁厚變薄，甚至出現拉裂，切向壓應力的作用使內側壁厚增厚，這都極大損傷了成形后防護梁的性能。在影響壁厚變化的因素中，工藝參數是直接關系到防護梁成形過程好壞的關鍵性因素，因此探究工藝參數對型材繞彎成形壁厚變化的影響規律，不僅可以為保持防護梁的關鍵性能提供技術保證，而且對完善型材成形理論有重要的意義。

現如今國內外的學者對型材的壁厚變化研究了很多，劉海龍等[6]通過建立QSTE700高強鋼矩形焊管的連續本構關系，更準確地分析厚度變化規律。趙冬梅等[7]運用正交試驗探究間隙、芯棒伸出量、摩擦等工藝參數對薄壁管繞彎時壁厚變化的影響。方軍等[8—10]利用正交試驗分別以材料的力學性能、工藝參數和間隙方面分析了高強鋼管的壁厚變化規律，得到了間隙較優解，并且試驗與模擬結果具有一致性；馬媛媛等[11]研究了繞彎時芯棒的直徑、芯頭間距及芯頭寬度等工藝參數對薄壁管壁厚變化的影響。梁闖等[12]深入研究了間隙對高強鈦管繞彎成形后的截面畸變和壁厚變化影響規律。劉寬心等[13]通過實驗探究了模具對鋁合金薄壁管的壁厚變化影響。以上研究僅限于截面簡單、尺寸較小的圓管或矩形管，因此得出的規律雖有參考價值但并不能用于指導本項目防護梁產品繞彎成形的工作。

文中以B700L高強鋼型材為研究對象，通過ABAQUS有限元模擬，結合正交試驗方法，探究彎曲半徑、間隙、芯模的芯頭個數對型材壁厚變化的影響及影響的主次關系。這對防護梁的優質生產具有一定的指導意義。

1 繞彎工藝有限元模型的建立

1.1 材料模型

建立有限元模型時，選用材料為B700L高強鋼，總型材長度為1600 mm，截面尺寸為120 mm×80 mm，厚度為2.5 mm，型材橫截面如圖1所示。利用常溫下單向拉伸試驗得到了材料的基本力學性能參數：彈性模量為216.21 GPa，伸長率為19.24%，屈服強度s為727.79 MPa，泊松比為0.22。

1.2 有限元模型的建立

利用ABAQUS/Explicit軟件的動態顯式模塊建立的適用于“日”字形截面型材兩端繞彎的三維有限元模型如圖2所示。固定彎曲模緊壓型材的非彎曲端不動，然后將芯模（由芯棒和芯頭組成）插入型腔內部，而為避免應力集中，滾輪需帶動活動壓模使型材慢慢彎曲到規定角度30°。對型材應用四節點四邊形殼單元S4R建模，對彎曲模、活動壓模、滾輪、芯模應用離散剛體單元R3D4建模。型材與模具間的接觸采用面與面接觸對，并應用庫侖摩擦模型描述接觸對的摩擦，摩擦因數在0.1~0.15間選擇。最后采用速度和角速度、位移和轉角、對稱/反對稱固定3種邊界條件真實地反映型材的繞彎過程。

由于型材存在焊縫，對焊縫區域利用Tie約束綁定，忽略焊縫影響做無縫處理。實際繞彎時型材需兩端同時彎曲，因此基于繞彎裝置結構和所受載荷的對稱性，故可利用1/2模型進行分析模擬。

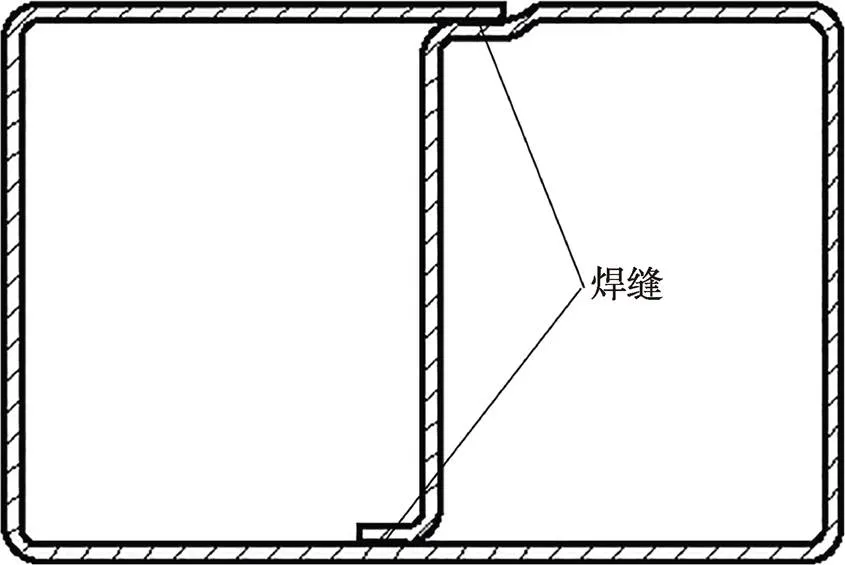
圖1 型材的橫截面示意

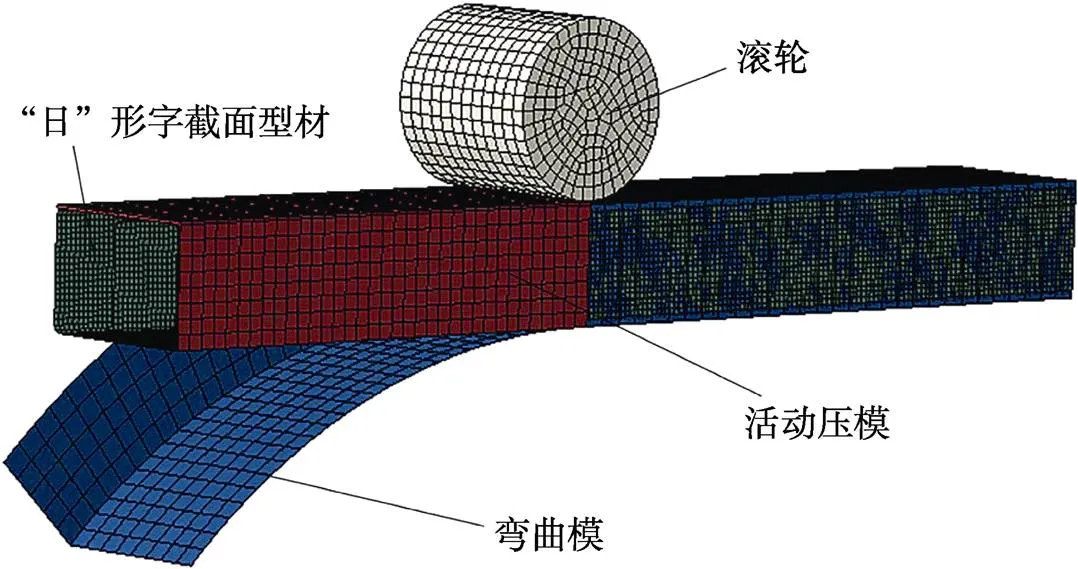
圖2 繞彎裝置的有限元模型

2 繞彎過程中型材厚度變化的研究方法

2.1 型材厚度變化研究的計算公式

由于文中應用殼單元[14]對“日”字形截面型材進行建模，殼單元不僅可以保證計算效率還能將網格劃分更細，使計算結果更加精確，并且只需在ABAQUS中設置STH（厚度）輸出變量，計算成功后可直觀地顯示型材各部分的厚度值。

利用式（1）[15]計算即可得到此部分的厚度變化率：

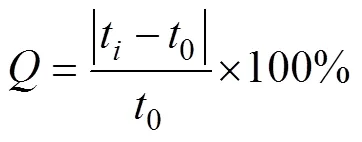
式中：t為繞彎后型材外側或內側的厚度值；0為型材的初始厚度值；為厚度變化率。

2.2 正交試驗設計

型材在繞彎成防護梁過程中，工藝參數對型材的繞彎成形效果影響極大。為探究工藝參數對繞彎成形壁厚變化的綜合影響，并確定各工藝參數對型材壁厚變化影響的主次關系，因此必須設計正交試驗。文中結合防護梁的成形過程及閱讀文獻綜合分析，確定5種對成形影響較大的工藝參數：芯模與型材的間隙，芯模的芯頭個數，彎曲半徑，型材與彎曲模間隙和活動壓模與型材間隙，具體繞彎工藝參數如表1，設計出正交試驗表L16(45)，以此來研究型材彎曲段外側的減薄率和內側的增厚率。

表1 型材繞彎工藝參數

Tab.1 Process parameters of profiles in rotary drawing bending

3 正交試驗模擬結果

3.1 型材彎曲區域外側的壁厚減薄率

根據正交試驗表設計16組不同組合的工藝參數，在ABAQUS中進行設置，完成模擬試驗，最后通過后處理分析型材繞彎成形后的壁厚變化情況，計算型材彎曲區域外側的壁厚減薄率，如表2所示。

表2 彎曲區域外側減薄率

Tab.2 Thinning rate outside the bending area

根據正交試驗表和各試驗條件下得到的外側減薄率數據，計算得出各工藝參數水平下繞彎后型材外側的平均壁厚減薄率，而為更直觀地探究壁厚變化規律，因此做出平均壁厚減薄率隨各工藝參數的變化趨勢，如圖3所示。

對各影響因素做極差分析的公式為：

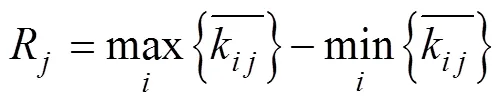
式中：Rj是某因素的極差；是某因素的綜合平均值的最大值；是同一因素綜合平均值的最小值。

依據式（2）進行極差計算得，彎曲半徑極差R是12.246 25，芯模間隙極差R是2.485 75，芯頭個數極差R是5.27，活動壓模間隙極差R是0.931 75，彎曲模間隙極差R是2.103，總體呈現R>R>R>R>R的趨勢。由此可以看出，彎曲半徑和芯頭個數對減薄率影響最大，其余參數影響較小。這正與圖3中減薄率隨著彎曲半徑因素水平和芯頭個數因素水平變化而急劇變化的趨勢一致。

究其原因是在繞彎過程中，型材外側減薄的本質是外側切向拉應力超過屈服應力，使金屬發生塑性流動，導致型材外側拉伸而厚度減小。當彎曲半徑越小時彎曲變形程度越劇烈，使型材外側切向拉應力越大，導致減薄率增大。值得注意的是，彎曲半徑= 340 mm下的平均減薄率為17.736 25%，已無比接近材料的最大伸長率=19.24%，因此制件有嚴重的損壞危險。

隨著芯頭個數增多，平均減薄率增大，呈正比趨勢。這是因為芯頭個數越多填充效果越好，就越容易增大與型材內腔的作用面積，使型材在繞彎時需要克服更大的摩擦力才能成形成功，所以導致了外側切向拉應力的增大，致使壁厚減薄率增大。

3.2 型材彎曲區域內側的壁厚增厚率

與型材外側減薄率研究方法類似，型材繞彎后彎曲區域內側的增厚率見表3。

表3 彎曲區域內側增厚率

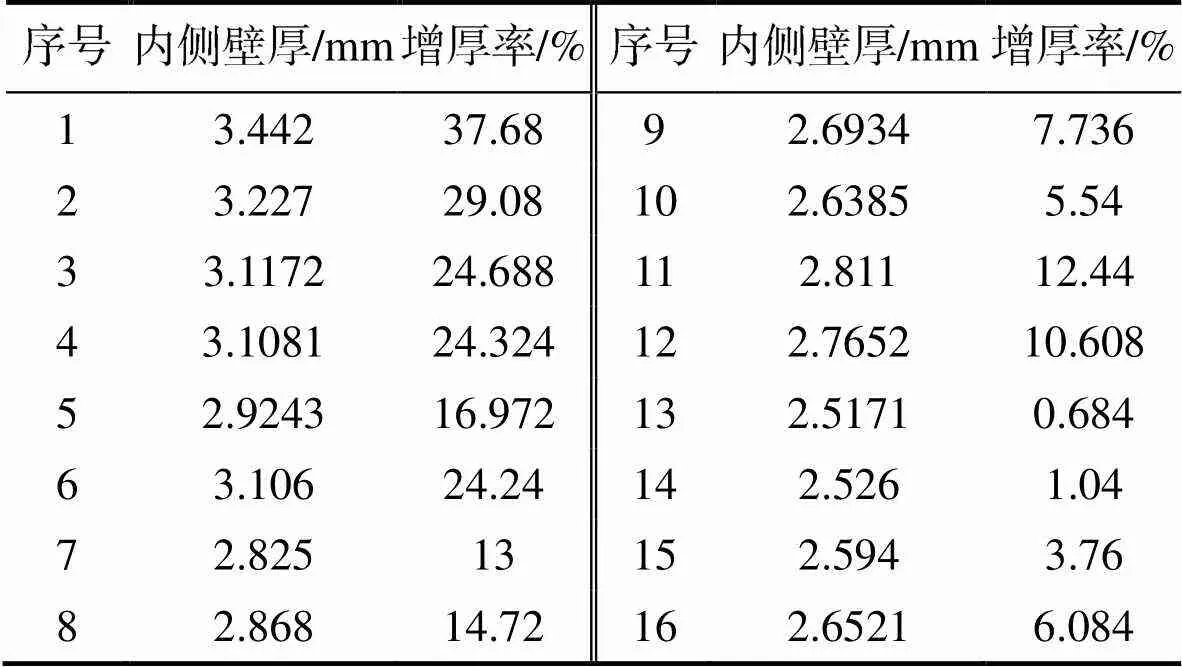
Tab.3 Thickening rate inside the bending area

計算得出各工藝參數水平下繞彎后型材內側的平均壁厚增厚率，并做出平均壁厚減薄率隨各工藝參數的變化趨勢，見圖4。

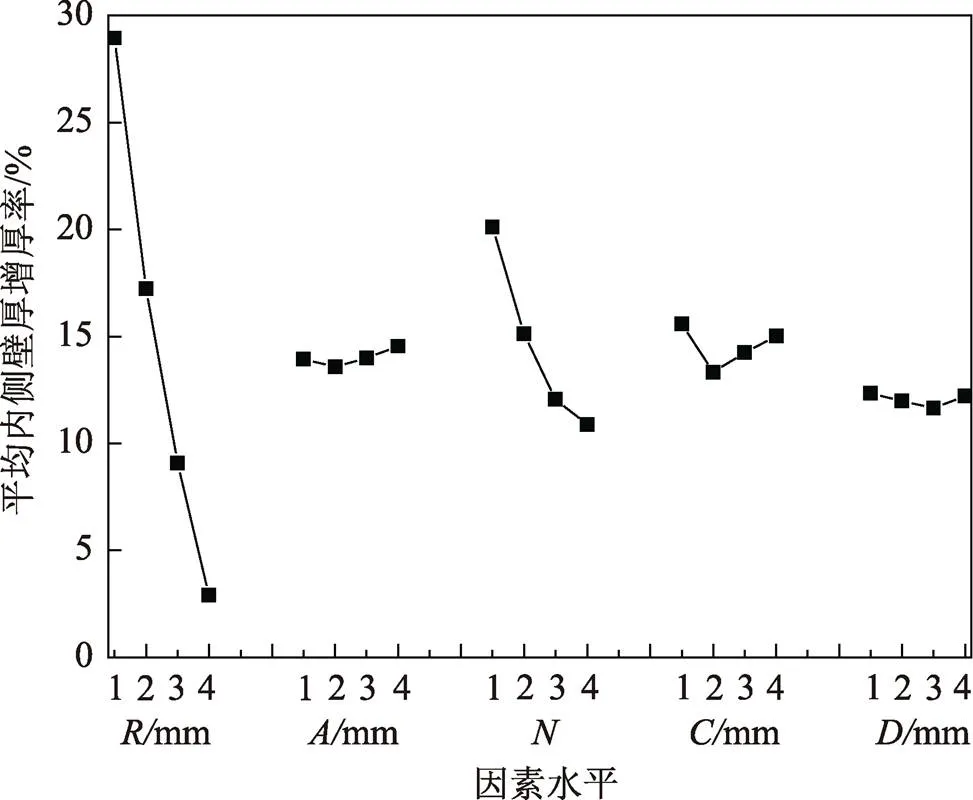
圖4 平均內側壁厚增厚率變化趨勢

與研究外側減薄率的極差分析方法類似，依據極差公式計算得，彎曲半徑極差R為26.051，芯模間隙極差R為1.259，芯頭個數極差R為9.224，活動壓模間隙極差R為2.261，彎曲模間隙極差R為0.449，總體呈現R>R>R>R>R的趨勢。可以看出依然是彎曲半徑和芯頭個數對增厚率影響極大，活動壓模與型材的間隙幾乎不產生影響；其余工藝參數因素對增厚率影響較小。值得注意的是，如圖4所示，隨著彎曲半徑的增大，內側增厚率急劇減小，與外側減薄率規律一致，但對于芯頭個數，卻是隨著芯頭增多，減薄率也急劇減小，與上文減薄率規律對立。這是因為繞彎過程中，內側切向壓應力的壓縮作用使金屬流動聚積，導致型材內側增厚缺陷的產生。彎曲半徑越大，曲率越小，變形程度越小，繞彎相對“容易”，所以切向壓應力更小，導致型材內側厚度變化小。芯頭數越多增厚率越小的原因是芯頭個數越多，支撐效果越好，與型材內腔的接觸面積更大，從而抑制金屬流動聚積，因而內側壁厚變化程度小。

4 確定繞彎成形方案及試驗驗證

4.1 最終繞彎成形工藝方案的確立

通過前文已分別得到對型材外側壁厚減薄率和內側壁厚增厚率影響效果較大的工藝參數及其影響機理。繪制圖5以確定文中工藝參數的最優解從而減輕防護梁成形時的壁厚變化缺陷，原理是觀察圖5a—b的各工藝參數影響曲線在4種因素水平條件下是否存在最小值，此最小值對應的因素水平即為這一工藝參數的最優解。

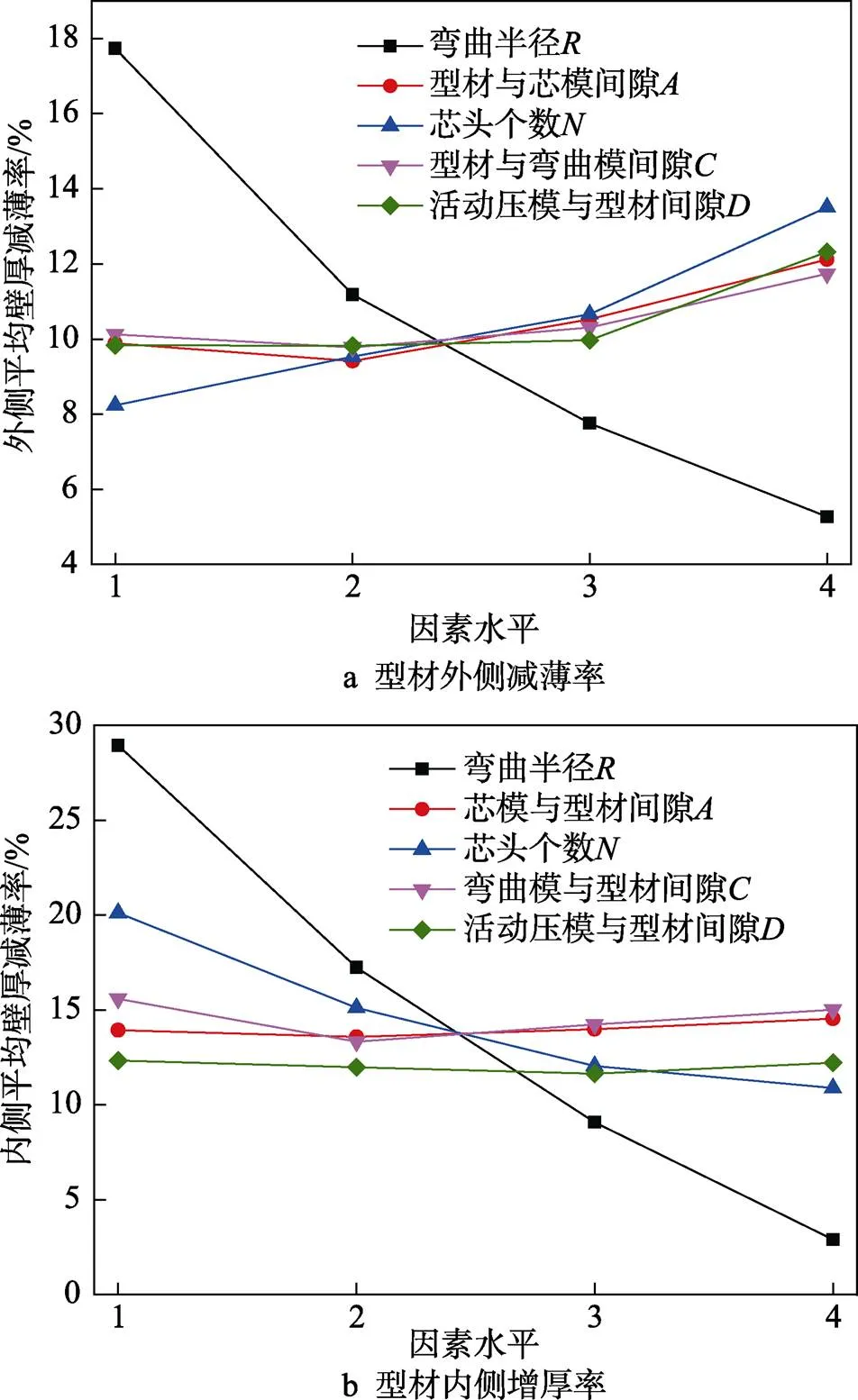
圖5 不同工藝參數影響下型材的壁厚變化

通過圖5a—b的對比和綜合分析，已經統一的最優工藝參數如下：為640 mm，為0.75 mm，為0.2 mm，為0.3 mm。對于芯模芯頭個數，由于它在減薄率和增厚率規律中對立，因此需控制其余工藝參數變量（為640 mm，為0.75 mm，為0.2 mm，為0.3 mm），只改變芯頭個數并設計試驗，見表4，利用ABAQUS有限元模擬得出各試驗的減薄率和增厚率，分析獲得最優芯頭個數解。

表4 以芯頭個數為變量的實驗制件的壁厚變化

Tab.4 Wall thickness changes in the experiment with the number of core heads as the variable

芯模芯頭個數對型材壁厚變化的影響見圖6，可以看出外側減薄率是隨芯頭增多而增大，且每增加一芯頭，減薄率增加幅度大致相同。內側增厚率雖然隨著芯頭增多而減小，但從芯頭數目為2之后曲線接近平緩，而芯頭數為3時，降低增厚率的程度雖然最大，但卻也顯著增大了減薄率，所以在針對減輕型材壁厚變化方面，芯頭個數應在0，1，2中選擇。

不同芯頭個數下的有限元模擬見圖7，可以看出芯模的芯頭數為0和1時，截面畸變極其嚴重，極大損壞了防護梁的性能，因此確定最終方案為：為640 mm，為0.75 mm，為2，為0.2 mm，為0.3 mm，而下一步還需要進行試驗來驗證模擬的有效性。

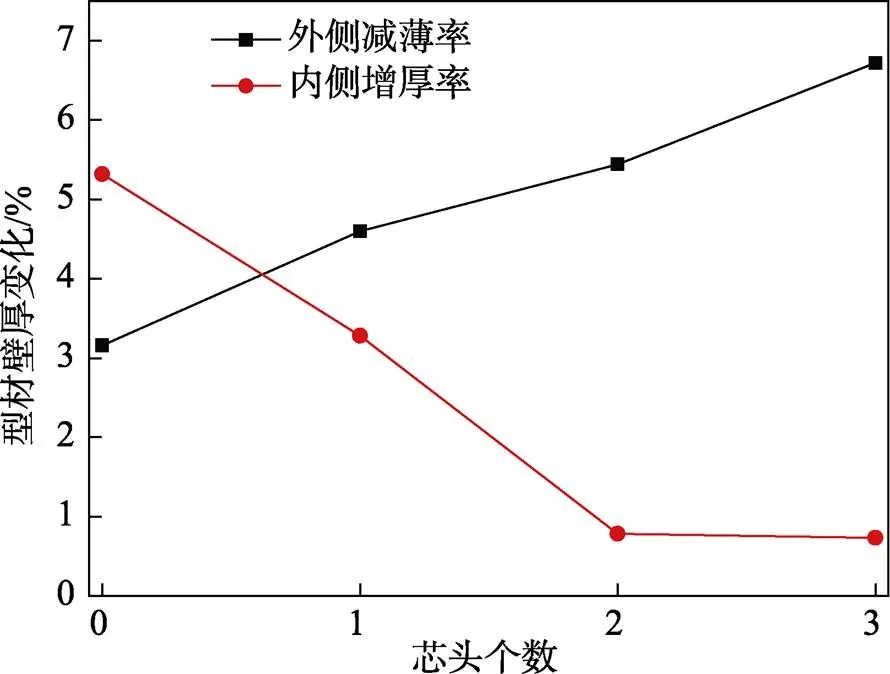
圖6 芯頭個數對型材壁厚變化影響

圖7 不同芯頭個數下的有限元模擬

4.2 試驗驗證

應用繞彎裝置在為640 mm，為0.75 mm，為2，為0.2 mm，為0.3 mm的工藝參數條件下，型材繞彎成防護梁制件的過程見圖8。為驗證上述仿真模型的有效性，以制得的防護梁制件為研究對象，測量繞彎后制件彎曲區域內外兩側的壁厚變化并與模擬結果比較。

圖8 應用繞彎裝置制備防護梁制件

將繞彎后獲得的防護梁制件放置在三坐標測量儀的測量空間，利用PROCMM對制件整體進行紅外線掃描，將掃描結果輸入電腦中構建3D圖像，然后利用Geomagic Qualify軟件對制件的3D圖像進行3D分析，最終得到防護梁制件外側減薄率和內側增厚率的最大值。實測數據如下：外側減薄率為5.60%，內側起皺率為0.828%；而模擬數據如下：外側減薄率為5.44%，內側起皺率為0.784%。通過對比可以得出模擬和試驗中減薄率的誤差約為0.16%，增厚率誤差約為0.044%，這是由加工誤差引起是不可避免的，但誤差極小，可以忽略不計，因此可以證明模擬和實驗結果吻合較好，試驗驗證了仿真模擬的有效性。

5 結語

1）“日”字形截面型材在繞彎成形為汽車防護梁的過程中，彎曲區域外側受切向拉應力，內側受切向壓應力的影響，這是導致外側壁厚減薄與內側壁厚增厚的主要原因。

2）采用有限元與正交試驗相結合方法，并采用極差分析得到工藝參數對壁厚的影響：外側壁厚減薄率隨彎曲半徑增大而減小，隨芯頭個數增多而增大，其余參數影響較小；內側壁厚增厚率隨彎曲半徑和芯頭個數的增大而減小，其余參數影響較小。

3）通過綜合分析確定最優工藝參數，最終得到較好的型材繞彎成形工藝方案如下：為640 mm，為0.75 mm，為2，為0.2 mm，為0.3 mm。然后以此實驗條件制得防護梁制件后，測得減薄率和增厚率模擬數值與試驗數據比較吻合，從而驗證了模擬結果的正確性

[1] 梁策, 王愛成, 李義. 復雜截面商用車防護梁型材繞彎成形裝置開發[J]. 科技資訊, 2019, 17(20): 60—62. LIANG Ce, WANG Ai-cheng, LI Yi. Development of the Rotary Draw Bending Forming Device for the Protective Beam Profile of the Commercial Vehicle with Complex Cross Section[J]. Science & Technology Information, 2019, 17(20): 60—62.

[2] 王愛成. 商用車防護梁輥彎與繞彎成形技術研究[D]. 長春: 吉林大學, 2019: 1—12. WANG Ai-cheng. Research on Roll Forming and Pure Rolling Rotary Draw Bending Technologies of Commercial Vehicle Bumper Beam[D]. Changchun: Jilin University, 2019: 1—12.

[3] LIANG Ji-cai, CHEN Chuan-dong, LIANG Ce, et al. One-Time Roll-Forming Technology for High-Strength Steel Profiles with “日” Section[J]. Advances in Materials Science and Engineering, 2019, 2019: 1—10.

[4] HEGGEMANN T, HOMBERG W. Deep Drawing of Fiber Metal Laminates for Automotive Lightweight Structures[J]. Composite Structures, 2019, 216: 53—57.

[5] CHANG Fei, DONG Ming-yu, LIU Min, et al. A Lightweight Appearance Quality Assessment System Based on Parallel Deep Learning for Painted Car Body[J]. Ieee Transactions on Instrumentation and Measurement, 2020, 69(8): 5298—5307.

[6] LIU Hai-long, LIU Yu-li, YANG Zhong, et al. Determination of Continuous Constitutive Relationship of Weld Zone of High-Strength Steel Rectangular Welded Tube[J]. Journal of Iron and Steel Research International, 2020, 27(10): 1212—1225.

[7] 趙冬梅, 巫帥珍, 賈傳偉, 等. 薄壁管繞彎工藝參數對壁厚影響分析[J]. 機械設計與制造, 2016(6): 179—183. ZHAO Dong-mei, WU Shuai-zhen, JIA Chuan-wei, et al. Analysis of Bending Technological Parameters on Wall Thickness of Thin-Walled Tube[J]. Machinery Design & Manufacture, 2016(6): 179—183.

[8] 方軍, 魯世強, 王克魯, 等. 材料力學性能對管材數控繞彎成形時壁厚變化的影響[J]. 機械工程材料, 2016, 40(4): 75—79. FANG Jun, LU Shi-qiang, WANG Ke-lu, et al. Effect of Material Mechanical Properties on Wall Thickness Variation in Numerical Control Rotary Draw Bending Process of Tubes[J]. Materials for Mechanical Engineering, 2016, 40(4): 75—79.

[9] 方軍, 魯世強, 王克魯, 等. 工藝參數對21-6-9高強不銹鋼管數控彎曲壁厚減薄影響的顯著性分析[J]. 中國機械工程, 2015, 26(9): 1233—1238. FANG Jun, LU Shi-qiang, WANG Ke-lu, et al. Significance Analysis of Effect of Process Parameters on Wall Thinning for 21-6-9 High Strength Stainless Steel Tube NC Bending[J]. China Mechanical Engineering, 2015, 26(9): 1233—1238.

[10] FANG Jun, LU Shi-qiang, WANG Ke-lu, et al. Three-Dimensional Finite Element Model of High Strength 21-6-9 Stainless Steel Tube in Rotary Draw Bending and Its Application[J]. Indian Journal of Engineering and Materials Sciences, 2015, 22(2): 141—152.

[11] 馬媛媛, 錢未騻, 張小巖, 等. 芯軸參數對薄壁管數控繞彎成形壁厚的影響研究[J]. 熱加工工藝, 2016, 45(21): 121—124. MA Yuan-yuan, QIAN Wei-shuang, ZHANG Xiao-yan, et al. Effect of Mandrel Parameters on Wall Thickness of Thin-Walled Tube in NC Potary Draw Bending Forming[J]. Hot Working Technology, 2016, 45(21): 121—124.

[12] 梁闖, 魯世強, 方軍, 等. 間隙對TA18高強鈦管數控彎曲成形截面畸變及壁厚變化的影響[J]. 塑性工程學報, 2017, 24(6): 87—93. LIANG Chuang, LU Shi-qiang, FANG Jun, et al. Effect of Clearance on Cross Section Deformation and Wall Thickness Variation of TA18 High Strength Titanium Tube in NC Bending[J]. Journal of Plasticity Engineering, 2017, 24(6): 87—93.

[13] LIU Kuan-xin, LIU Yu-li, YANG He. Experimental Study on the Effect of Dies on Wall Thickness Distribution in NC Bending of Thin-Walled Rectangular 3A21 Aluminum Alloy Tube[J]. International Journal of Advanced Manufacturing Technology, 2013, 68(5/6/7/8): 1867—1874.

[14] 丁源. 2018有限元分析從入門到精通[M]. 北京: 清華大學出版社, 2018: 354—369. DING Yuan. 2018 Finite Element Analysis from Entry to Master[M]. Beijing: Tsinghua University Press, 2018: 354—369.

[15] 徐小兵, 官強. 圓管繞彎壁厚變化的數值模擬研究[J]. 鍛壓技術, 2010, 35(6): 133—136. XU Xiao-bing, GUAN Qiang. Numerical Simulation of Wall Thickness Change in Tube Bending[J]. Forging & Stamping Technology, 2010, 35(6): 133—136.

Research on the Influence of Process Parameters on the Wall Thickness of the Protective Beam after Rotary Draw Bending

DING Li-bo1, LIANG Tian2, LI Ming-jie1, LIANG Ji-cai2

(1. Baicheng Vecational and Technical College, Baicheng 137000, China; 2. College of Materials Science and Engineering, Jilin University, Changchun 130000, China)

The purpose of this article is to explore the influence of process parameters on the wall thickness of the profile with “日”-shaped section when the profile is rotary draw bending into the protective beam for commercial vehicles, so as to improve the product quality of the protective beam. Based on the finite element simulation analysis, the orthogonal experimental design was used to simulate the forming process of the profile under different process parameters ratio, and the range analysis on the thickness reduction of the outer wall and the increase of the inner wall thickness in the bending area of the profile are conducted. Finally, the research shows that the bending radius and the number of core heads of mandrel have a great influence on the outer thinning rate and inner thickening rate, and other parameters have relatively little influence. Based on the results of the orthogonal experiment and comprehensive analysis, a better rotary draw bending plan of the protective beam is finally established and the validity of the simulation results is verified through experiments. Studies have proved that selecting the appropriate combination of process parameters ratio can significantly reduce the wall thickness changes of the profile, thereby greatly improving the product quality of the protective beam.

rotary draw bending; profile with “日”-shaped section; orthogonal experiment; the finite element simulation analysis; process parameters

10.3969/j.issn.1674-6457.2021.02.017

TG306

A

1674-6457(2021)02-0105-06

2020-12-29

丁立波（1962—），女，副教授，主要研究方向為材料成形。

李明杰（1971—），男，碩士，教授，主要研究方向為材料加工工程。