山谷地形對入射SV波地震反應分析

卓發成

(上海隧道工程股份有限公司, 上海 200023)

0 引言

強震動記錄和震害調查以及理論研究表明[1-4],局部地形條件會對地震波的傳播產生重要影響,使得地震動空間分布特征呈現顯著的差異。目前研究地形效應的方法主要有強震動地形效應觀測、解析法和數值模擬法[3]。地形效應觀測依賴臺陣的分布,解析法主要針對可使用簡單參數能描述的模型[5-7],數值計算方法適用于對復雜場地的地震反應模擬,可以彌補解析法在求解復雜場地時存在的不足。目前常用的數值計算方法有:有限差分法[8]、邊界元法[9]、譜元法[10-11]、有限元法[12-14]等。

其中,有限元法在處理計算模型的幾何和物理條件上具有優勢,因此運用最為廣泛。劉晶波[12]運用有限元法結合修正的透射人工邊界,研究了相鄰凸起地形中地震波傳播對地面運動的影響;榮棉水等[13]研究了兩個相鄰平臺狀凸起地形在不同入射角度的P波作用下頻譜特性的影響分析;金丹丹等[15]利用ABAQUS軟件研究典型復合地形場地對SH波的影響,結果表明,相鄰地形對特定頻段地震動放大效應與聚集效應比較明顯,局部地形變化將引起地震動持時差異,且持時和輸入地震動特性相關。

隨著我國經濟建設快速發展,大量的高速公路、大型水壩、長輸電塔(線)等大型工程項目的涌現,多地貌單元復合場地的地震反應分析越來越受到重視。在我國《建筑抗震設計規范》[16]中也明確規定:對復雜地形或地形變化明顯的建筑場地,應估計不利地段對設計地震動參數的放大作用。本文在顯式有限元方法的基礎上結合黏彈性人工邊界研究了具有單一突出平臺的山體地形和相鄰山體地形對地表地震動特性的影響,并分析了相鄰凸起之間距離變化對計算結果的影響。

1 計算模型及輸入地震動

單一凸起山體地形和具有兩個凸起山體地形的計算模型如圖1所示。假設所有凸起平臺寬度與高度均為R,大小為50 m,坡角均為45°,相鄰凸起之間的距離為d,計算區域的寬和高均為250 m,所有模型均為均質、各向同性、線彈性介質,具體參數列于表1。由于實際地震動的頻段往往較寬,為了研究頻段內不同觀測點地面運動的特性,入射地震波為垂直入射的SV波,其時程曲線及傅里葉幅值譜如圖2所示。

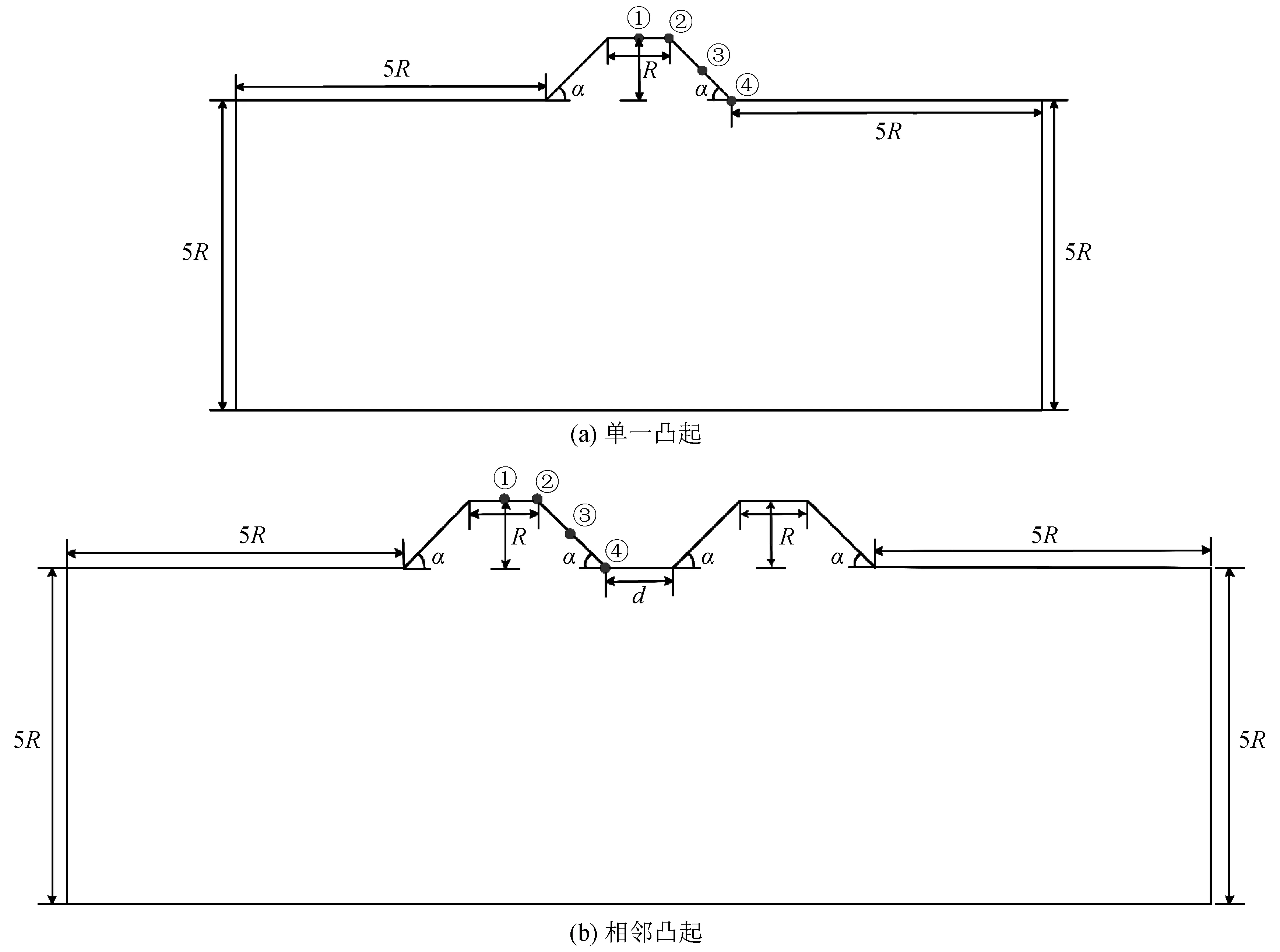
圖1 單一凸起與相鄰凸起山體地形模型示意圖Fig.1 Terrain models with single and adjacent hills

表1 模型介質參數

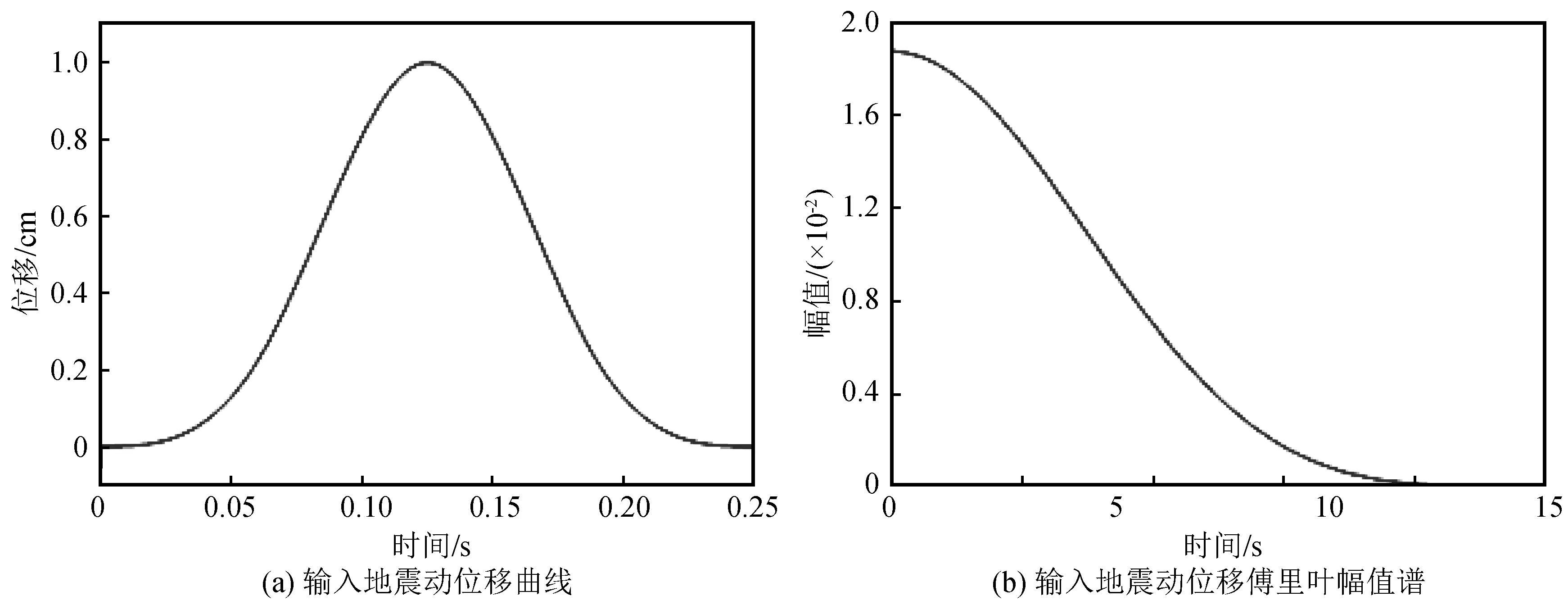
圖2 輸入地震動位移時程及傅里葉幅值譜Fig.2 Displacement time-history and its Fourier spectrum of incident earthquake wave

2 計算方法

2.1 集中質量顯式有限元的內點計算方法

集中質量顯式有限元的實質是根據當前時刻的節點運動方程求解下一時刻節點的運動,它不需要進行剛度、質量、阻尼陣的集成,這樣整個計算只需要很小的高速存貯區,計算效率較高。尤其當一系列單元的剛度陣、質量陣、阻尼陣相同時,就不需要重復計算,效率更高。

對于內點,由動力平衡條件可建立運動方程:

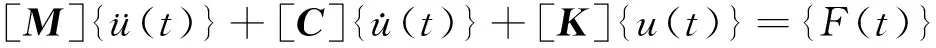
(1)

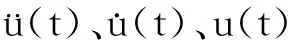
對于運動方程式(1),采用中心差分法得到逐步積分格式:

[M]{u(t+Δt)}=[M](2u(t)-{u(t-Δt)}-Δt2[K]{u(t)}-Δt[C]({u(t)}-

{u(t-Δt)}))+Δt2{F(t)}

(2)

2.2 黏彈性人工邊界

劉晶波等[17]根據波動方程給出了二維黏彈性動力人工邊界參數:

切向:

(3)

法向:

(4)

式中:Kbn、Kbt分別為法向與切向的彈簧系數;,r為散射源至人工邊界點的距離,在場地反應中,一般將地表中心點假定為散射源;G為剪切模型;αT與αN為人工邊界參數,本文中分為取值為0.5和1.0;Cbt、Cbn分別為法向與切向的阻尼系數,cS與cP分為S波和P波波速。

一致黏彈性人工邊界單元的剛度矩陣為:

(5)

(6)

直接將式(5)、(6)的單元剛度以及阻尼矩陣組裝到原結構整體剛度矩陣中,便可以完成黏彈性人工邊界的施加。

2.3 方法驗證

二維有限元模型計算尺寸為200 m×400 m,頂端為自由表面,單元網格尺寸為5 m×5 m。模型介質材料參數列于表1。在底部垂直向上入射x方向單位脈沖剪切位移波,入射波位移時程及其傅里葉幅值譜見圖2。圖3給出了基于黏彈性人工邊界的顯式有限元方法計算得到的模型底部、中部、頂部3個觀測點的水平向位移時程曲線與理論解的比較。由圖3可知,入射波由底部向上傳播在自由地表發生反射,自由地表處的位移幅值為輸入波幅值的兩倍,下行波從底邊界,沒有發生反射現象。本文的計算結果與理論解吻合得很好,證明了本文計算方法的正確性和有效性。

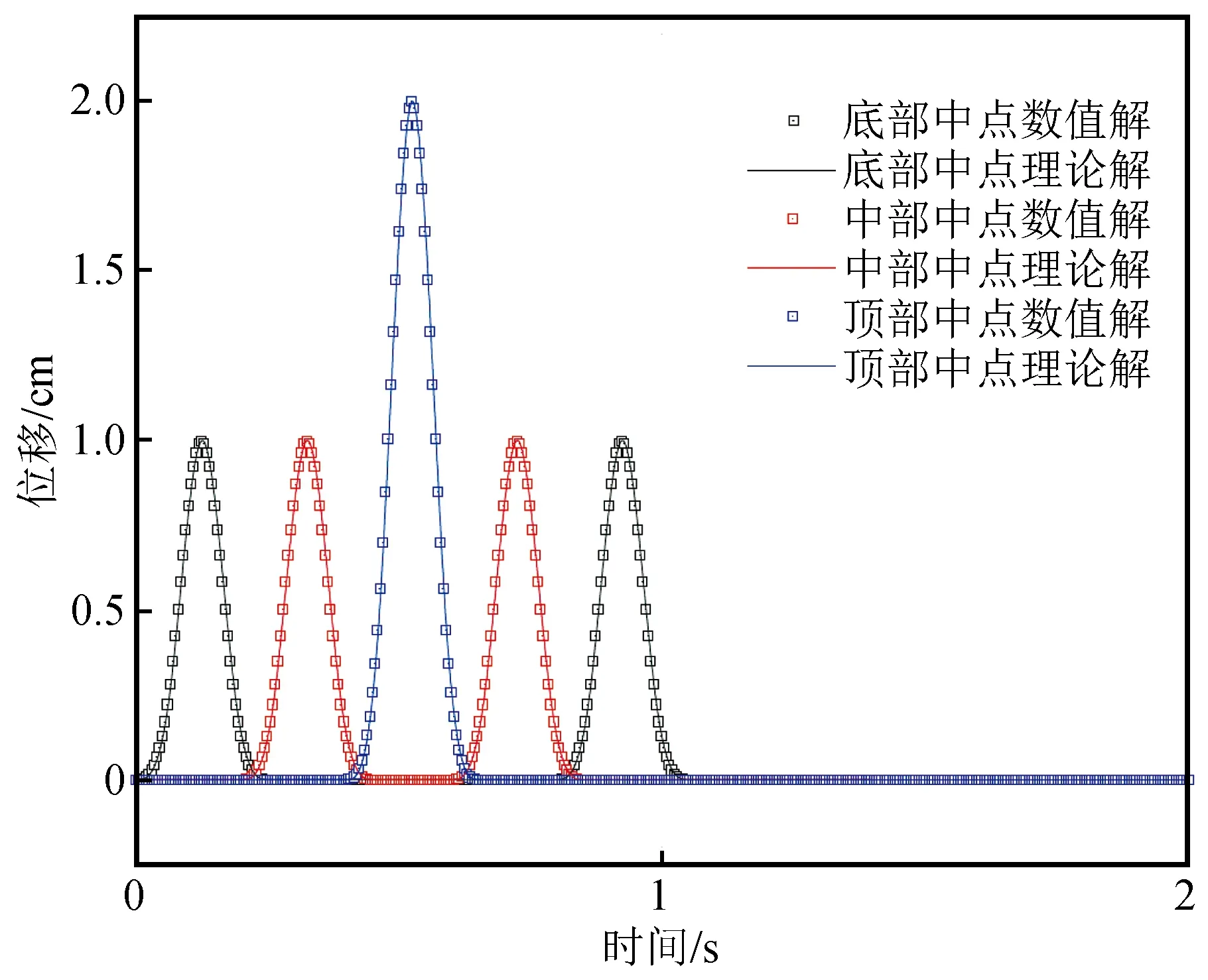
圖3 數值計算結果與理論解比較Fig.3 Comparison of numerical results and the theoretical solution

3 凸起山體地形對地震動反應譜特性的影響

首先,以單一凸起山體地形模型為例分析山體地形對地表地震動特性的影響效應。圖4為單一凸起山體地形模型在SV波垂直入射的情況下地表峰值位移(PGD)分布情況,從圖4可以發現:(1) 由于單一凸起山體地形是以觀測點1為中心的軸對稱模型,且入射波為垂直入射的SV波,因此整個模型的PGD分布情況也呈現出對稱形式;(2) 從山腳至山頂處的PGD逐漸增大,但是在山頂平臺處的PGD出現了降低的趨勢;(3) 地表同一監測點沿著x軸方向的反應較y軸方向更為強烈。可以初步判斷局部凸起的山體地形的存在使得地表各點處的地震動發生了變化,主要表現在放大了山頂的地面運動,山腰和山腳處的地面運動有所減小。

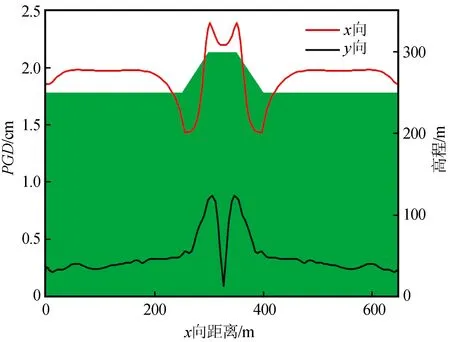
圖4 單一突起山體模型地表PGD分布圖Fig.4 Distribution of surface PGD of the model with single hill

為了進一步研究地形對地表運動的影響,圖5給出了4個觀測點沿水平方向的位移時程、位移傅氏譜及譜比。譜比為凸起山體地形條件下觀測點的地震動位移傅氏譜與均勻半空間場地自由地表的地震動位移傅氏譜的比值。從圖5中可以發現觀測點1在2.5～8 Hz這一頻段內的譜比略小于1,在0～2.5 Hz和8～10 Hz這兩個頻段的譜比大于1。觀測點2在0～10 Hz整個頻段內的譜比均大于1。觀測點1和觀測點2均在山頂處,但觀測點1位于山頂平臺處,表明相鄰地形會對地震動的頻譜產生放大作用。觀測點3位于山腰處,在0～1.5 Hz和5.5～7.5 Hz這兩個頻段內的頻譜幅值有所放大。觀測點4位于腳處,其放大的頻段范圍最小。

以下為地震動輸入一致的條件下,分析相鄰凸起山體地形對地表地震動的影響定義ξ=d/R。圖6給出了相鄰凸起山體之間距離變化時地表PGD分布圖,可以發現由于兩個相鄰的山體具有對稱性,其地表PGD的分布也具有對稱性,同時可以發現沿著x軸方向的PGD數值整體上大于沿著y軸方向的PGD數值,表明沿著地震動輸入方向的地表反應較其他方向的反應更為強烈,這與單一凸起山體地形條件下模擬結果類似。

圖7給出了相鄰凸起山體之間距離改變時對地表4個觀測點的PGD影響,4個觀測點的位置如圖1(b)所示。由圖7可知當ξ逐漸增加時,觀測點1、2和點3沿著x軸方向上變化趨勢很小,但是位于山腳處的觀測點4呈現出先增大后不變的趨勢;當ξ為2時,這4個觀測點PGD的變化趨勢逐漸穩定,此時這4個觀測點的PGD依次減小;在y軸方向上觀測點1和觀測點2呈現出逐漸減小的趨勢,位于山峰處的觀測點3和位于山腳處的觀測點4都呈現出先增大后減小的變化趨勢。當這4個觀測點在y軸方向的PGD逐漸趨于穩定時位于上頂平臺處觀測點1的PGD值最小。同時可以發現,位移在山腳處的觀測點4隨著ξ改變時PGD在x軸和y軸方向上的改變是最大的,分別為16%和587.5%。

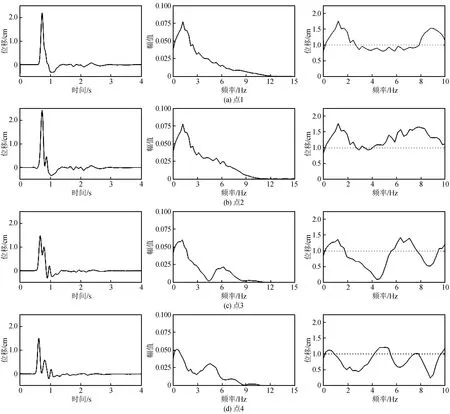
圖5 單一突起山體模型地表不同觀測點的位移時程、頻譜及譜比Fig.5 The displacement time histories, frequency spectra, and spectrum ratio at differentobservation points derived from the model with single hill

為了進一步研究相鄰凸起山體之間距離的變化對地表地震動的影響,圖8給出了相鄰凸起山體之間距離改時模型地表4個觀測點的位移時程、頻譜特性以及譜比的變化。可以發現這4個觀測點的位移時程曲線變化不大,但是從位移頻譜中可以發現隨著ξ的改變,在1～4 Hz這一頻段內的變化較為明顯,但是每個觀測點的卓越頻譜并未發生改變。從譜比中可以發現,位移在山頂平臺處的觀測點1放大頻段與單個凸起山體地形模型的計算結果相同,然而在7～10 Hz這一頻段內的譜比值明顯大于單個凸起山體地形模型的計算結果。觀測點2、3和4各個頻譜所對應的譜比值隨著ξ的改變而改變,但ξ對放大頻段的影響甚微。

4 討論與結論

基于顯式動力有限元計算方法和黏彈性人工邊界處理方法,探討了局部單一凸起及相鄰凸起的山地地形在垂直輸入SV波的情況下對地震動參數放大效應的影響。有如下結論:

(1) 地表地震動沿著輸入地震動方向的影響比其他方向的影響更大;

(2) 局部凸起地形對地表地震動有放大效應,從山頂至山腳處放大趨勢逐漸減小;

(3) 與單一凸起地形相比,相鄰地形的存在對地表地震動的譜比曲線形狀影響不大,但是隨著相鄰凸起之間距離的增加,其對PGD具有顯著的影響(就本文所涉及的算例而言,位于山腳處觀測點沿著地震動輸入方向的PGD最大可達到單一凸起放大倍數的1.16倍)。

圖6 相鄰凸起山體之間距離變化時地表PGD分布圖Fig.6 Distribution of surface PGD with different distance between adjacent hills

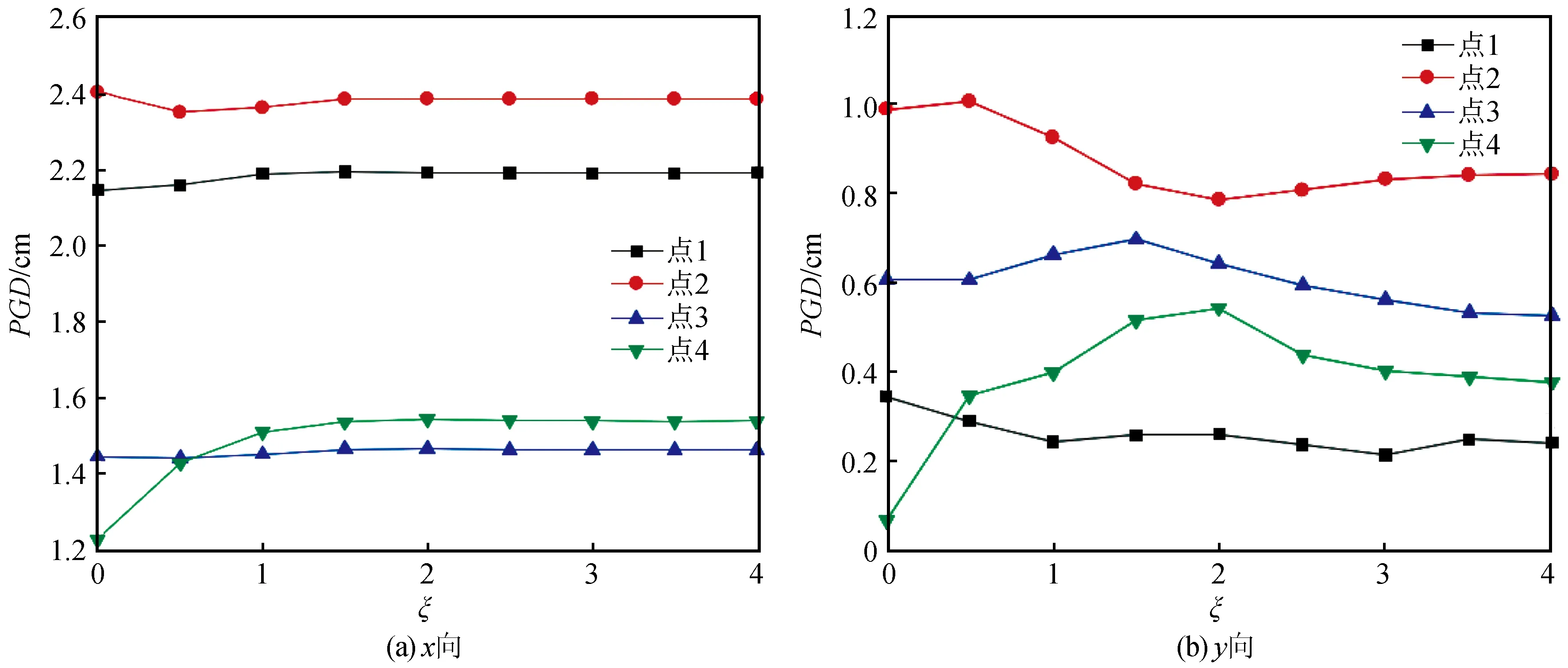
圖7 相鄰凸起山體之間距離對地表觀測點的PGD影響Fig.7 Effect of different distance between adjacent hills on the surface PGD

因此,在對局部地形對場地地表地震動的影響進行分析時,應對這種相鄰地形的動力相互作用效應對分析結果的影響加以重視。

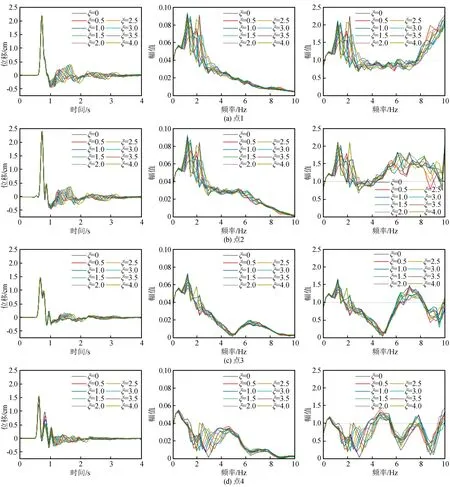
圖8 相鄰凸起山體之間距離變化時模型地表不同觀測點的位移時程、頻譜及傳遞函數Fig.8 The displacement time histories, frequency spectra, and transfer functions at differentobservation points of the model with different distance between adjacent hills