一種利用花粉算法優化的遙感圖像分割方法
段明義,盧印舉,蘇玉
(鄭州工程技術學院 信息工程學院,鄭州 450044)
0 引言
隨著遙感技術的不斷發展,人類獲得的遙感圖像越來越豐富。遙感圖像與自然圖像有著明顯區別,是一種十分重要的信息資源[1]。為了能夠從遙感圖像中提取出感興趣的信息,人們提出了很多方法,圖像分割是常用的一種。該方法主要是通過將一幅需要處理的圖像根據一定的算法劃分為不同的區域,以達到提取出感興趣信息的目的。圖像分割是圖像分析中關鍵的一步,目前主要有基于閾值的、基于區域的、基于邊緣理論的以及基于特定理論的方法[2-4]。
聚類作為一種無監督分類技術,在遙感圖像分割中被廣泛應用。學者們通過使用該技術將遙感圖像中特征相似的像素點劃分到同一類中,使得類間相似度盡可能低。K-means是目前在圖像分割領域已經廣泛應用的一種聚類劃分方法[5]。該方法通過對定義的目標函數進行迭代、逼近,最終得到結果,其缺點主要在于需要事先人工設置、確定一系列的參數值,比如初始聚類數目;同時,圖像中的噪聲也能極大地影響結果[6]。花粉算法(flower pollination algorithm,FPA)模擬自然界顯花植物花朵的授粉過程,是一種仿生算法[7],該算法原理簡單、參數少、易于實現,同時具有良好的全局尋優能力。本文采用花粉算法來對K-means算法的初始參數進行優化,以期達到改進聚類效果的目的。高斯模型是常見的數據模型,可以用來對遙感圖像特征數據進行模擬,對于多個數據的模擬需將多個高斯模型根據權值系數結合在一起,即高斯混合模型(Gaussian mixture model,GMM)[8]。在實際應用中,高斯分布易受到噪聲值的干擾,同時,對于樣本尾部的擬合不如具有更長尾部的學生t分布(student’stdistribution)。本文算法引入學生t分布來替換高斯分布。
本文針對遙感圖像的特點,采用學生t分布混合模型(student’stdistribution mixture model,TMM)[9]對數據進行擬合。為提高擬合效果,采用改進的K-means聚類算法來優化混合模型的初始參數,同時使用EM算法對模型中的參數進行求解。本文方法為花粉K-meanst分布混合模型法(K-means student’stdistribution mixture model with FPA,KF_TMM)。
1 方法
1.1 學生t分布
隨著科學技術的發展,數據信息的獲取越來越方便,但對數據的處理卻顯得越來越復雜,一般都采用統計學方法。t分布又名學生分布,含有自由度參數v,其概率密度函數如式(1)所示。
(1)
式中:Γ(·)為Gamma函數。如圖1所示,當v=1時,t分布即為柯西(Cauchy)分布密度函數(t(v=1)=C(0,1)),當t(v→)=N(0,1),柯西分布與高斯分布是t分布2個邊界特例[10]。這為后文中的自適應變異提供了基礎。t分布變異恰好融合了柯西分布變異和高斯分布變異的特點,通過不斷改變自由度參數v的值可以獲得不同的變異幅度。

圖1 t分布、柯西分布、高斯分布函數分布圖
1.2 聚類算法
1)K-means。設遙感圖像中N個數據點為X={x1,x2,…,xN},xi表示第i個像素的灰度值,N表示圖像像素總數量。算法運行結果是將遙感圖像中的N個圖像數據點根據預先設置好的聚類個數K,劃分成K個遙感圖像子集(聚類)M1,M2,…,MK,子集中心分別為c1,c2,…,cK。目標函數如式(2)所示。
(2)
式中:x是來自遙感圖像子集Mj的樣本。
如果目標函數取得最小值,根據式(3)來更新K個圖像子集的中心點c1,c2,…,cK。
(3)
式中:cj、Nj分別代表第j個子集的中心和樣本數。聚類算法通過迭代,求出每個子集中心的最終位置,算法終止。
傳統K-means 聚類方法簡單、易實現且得到了廣泛應用,但其需要隨機選擇初始聚類中心,且需要事先確定初始中心點數目。本文針對此缺點采用花粉算法加以改進。
2)花粉算法。花粉算法主要來自于對自然界顯花植物授粉過程的模擬,是一種新型的元啟發式算法[11]。顯花植物主要通過授粉繁殖,這一般與花粉的轉移有關,而這種轉移通常與授粉媒介(如昆蟲、鳥類、蝙蝠和其他動物等)有關。授粉過程可采取2種主要形式:非生物的和生物的。大多數的開花植物是生物授粉,花粉是由昆蟲和動物等授粉媒介轉移。少部分的授粉采取非生物形式,不需要任何傳粉媒介。同一植物物種的授粉,可以在同株或異株之間進行,即自花授粉或異花授粉。FPA算法認為自花授粉、生物授粉為在局部區域尋找最優值,即局部尋優;異花授粉、生物授粉為在全局區域尋找最優值,即全局尋優。異花授粉中,授粉媒介(如蜜蜂、蝙蝠、鳥類和蒼蠅等)可以飛行很遠的距離,飛行行為認為是Levy飛行[12],其跳躍或飛行距離步長遵循Levy分布。花的恒定性即繁殖概率正比于參與授粉花朵的相似性。整個授粉過程在局部和全局授粉之間來回切換,切換時機由概率p控制,p∈[0,1]且稍微傾向于局部授粉。理想化的情況假設每株植物只開一朵花,每朵花只有一個花粉配子,不需要區分花粉配子、花朵、植物或問題的解,問題的解xi即花朵或花粉配子。
FPA算法有2個關鍵步驟,即全局授粉和局部授粉。

(4)
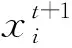
(5)
式中:Γ(λ)是標準Gamma函數,對大步長s>0有效,下文中,取λ=1.5。
(6)

大多數的授粉活動發生在局部或全局范圍。實際授粉過程中,花朵傾向于被臨近的或者不太遠的花朵授粉。因此,全局授粉與局部授粉之間轉換概率p的取值為0.8,而不是等概率的0.5。
實際運行過程中,花粉算法前期容易局限于局部最優解,后期接近最優解時,收斂速度慢。為了對其改進,本文借鑒文獻[13]中的思想,對花粉狀態Xi=(xi1,xi2,…,xin)進行自適應t分布變異,定義如式(7)所示。
(7)

本文主要利用FPA算法全局尋優能力強的優點,將其與K-means算法相結合,迅速找到接近全局最優的解。以此解輸入K-means算法作為K-means算法的初始聚類中心,然后執行K-means算法,發揮K-means算法局部尋優能力強的特點,最終找到最優解,以此作為有限混合模型參數求解的初始值。
1.3 t分布混合模型
高斯分布(Gaussian distribution)是統計學中常用的一種分布,通常用來描述樣本數據的分布情況,但由于其尾部較短,容易受到噪聲值的影響,數據擬合能力較差,特別是對于樣本數據邊緣。學生t分布是另一種常用的分布,式(1)為其概率密度函數,v代表自由度參數。從圖1可以看出,與高斯分布相比,t分布曲線更扁平一些、尾部更長,更適合用來模擬數據樣本的尾部。
多維(p維)學生t分布可以用式(8)表示。
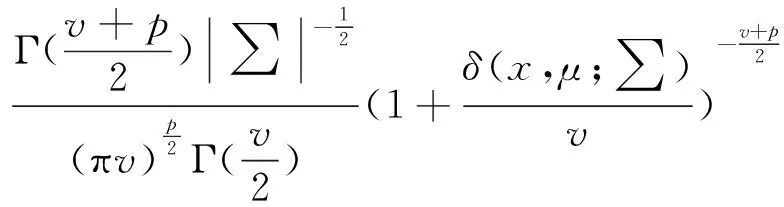
(8)
式中:δ(x,μ;∑)=(x-μ)T∑-1(x-μ)。與高斯模型相似,為了對多個數據進行模擬,需要將多個學生t分布模型根據權值系數結合在一起,即學生t分布混合模型,由式(9)表示。
(9)
式中:πk為混合系數。
上述TMM中未知參數的求解,可以使用EM算法來進行擬合[14]。
E步:
(10)
(11)
M步:
(12)
(13)
(14)
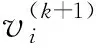
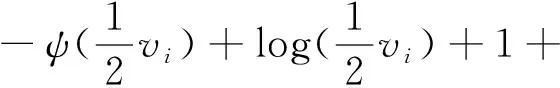
(15)

重復執行EM算法E步和M步,直到算法收斂或者滿足終止條件即可求出TMM中的參數。
感興趣樣本的混合分布模型確定后,借助于貝葉斯公式可以計算出每一個像素的后驗概率,進一步可確定每一個像素xi所屬的類別,從而完成圖像的分割。
2 實驗結果與分析
2.1 分割效果評價準則
實驗部分驗證本文所提算法的運行性能,主要從2方面來衡量,即誤分率(misclassification ratio,MCR)[15]和概率隨機(probabilistic rand,PR)索引[16]。
MCR取值范圍為[0,1],其值越小,表示分割結果越好。該指標主要表征圖像錯誤分割部分所占的比例。PR利用2個分割結果共同部分測量它們的一致性。PR∈[0,1],其值越大算法分割效果越好。
2.2 實驗結果與分析
為了驗證本文所提出的分割算法,在實驗部分,構建以Matlab 2012b為基礎的測試環境。硬件平臺主要指標為:8 GB內存以及英特爾酷睿3.2 GHzCPU。
實驗主要在合成圖像[17]和實際遙感圖像[18]上進行,以驗證算法的有效性和魯棒性。對比算法包括TMM、自適應均值濾波t混合模型(SMM-AM)[19]、基于馬爾科夫隨機場的t混合模型(SCSMM)[20]。本文方法為花粉K-meanst分布混合模型法(KF_TMM)。
實驗方案為:首先,分別對合成圖像添加高斯噪聲進行污染,運行各對比算法,進行結果分析;然后,針對真實遙感圖像,運行各算法并對結果進行對比分析。
1)合成圖像。圖2(a)為合成圖像原圖,圖2(b)為添加高斯噪聲(均值0,方差0.05)的圖像,圖2(c)至圖2 (f)為運行各算法的分割結果。

圖2 合成圖像分割結果對比
從圖2可以看出,各算法都可以進行分割但效果各異。TMM分割出來的圖像不論是淺色的區域還是深色的區域,雖然輪廓很清楚但圖中噪聲點明顯較多。SMM-AM和SCSMM 2種算法較傳統TMM結果有很大改進,各區域的邊界更加明顯,在對噪聲的抑制方面SCSMM優于SMM-AM,前者噪聲更少。圖2(f)為本文方法分割的結果。從圖中可以看出,相對于其他3種算法,噪聲明顯減少,分割出的區域界限分明,說明本文算法的抗噪性強。定量結果如表1所示。

表1 定量評估結果
從表1可以看出,本文算法在2個評價指標即誤分率(MCR)和概率隨機(PR)索引方面都優于其他對比算法。但是,本文算法在運行時間方面不是最優的,主要是因為該算法分別在聚類算法、花粉算法和混合模型方面都進行了改進,使得整體算法較復雜,增加了運行耗時。
為了驗證本文算法的抗噪性能,對合成圖像添加均值0,方差分別為0.01、0.03、0.05、0.07、0.09的高斯噪聲,運行本文算法。各噪聲下MCR和PR曲線對比結果如圖3所示。

圖3 抗噪性能對比圖
由圖3可以看出,隨著高斯噪聲方差的增大,MCR增加,說明在高噪聲下本文算法的分割效果有所降低,但從曲線圖可以看出曲線增幅不大,說明該方法受噪聲影響不大。同理可以看出,雖然噪聲會影響PR索引的值但影響不大,曲線降幅不大,說明本文方法抗噪性強。
2)實際遙感圖像。為進一步測試本文算法的有效性,在圖4(a)的實際遙感圖像上運行各算法進行分割,結果如圖4(b)至圖4(e)所示。
圖4結果顯示,各算法分割效果有明顯不同。TMM和SMM-AM分割出來的圖像輪廓清晰,但是對于船只和岸上建筑物的細節處理欠佳。SCSMM分割出來的圖像較前者有很大改進,建筑物清晰,基本能被識別出來,但對水域的劃分欠佳,整體的水域被劃分為不同的部分。本文方法分割的結果優于其他3種算法,圖中目標清晰,整個水域劃分為一體。定量結果如表2所示。

圖4 實際遙感圖像分割結果對比

表2 定量評估結果
從表2可以看出,本文算法在2個評價指標MCR和PR方面都優于其他對比算法。因為算法整體較復雜,運行耗時不如對比算法。
以上實驗結果表明本文算法分割圖像效果好,抗噪能力強。
3 結束語
本研究提出了一種新的遙感圖像分割方法,該方法主要基于聚類算法和t分布混合模型。為提高最終的圖像分割效果,使用花粉算法對聚類算法進行改進,使用EM算法求解t分布混合模型中的參數。將改進后的算法應用于仿真圖像和實際遙感圖像,運行結果表明,該算法抗噪能力強、精度高且分割效果好。

