調速側電力系統穩定器優化設計方法
林耀東
同濟大學 電子與信息工程學院 上海 201804
1 設計背景
低頻振蕩始終是電力系統穩定性中不可忽視的問題,無論是區域間低頻振蕩[1],還是局部低頻振蕩[2],都會給系統帶來極大的危害。
電力系統低頻振蕩通常指頻率在0.2~2.5 Hz范圍內的振蕩[3]。為研究電力系統的低頻振蕩問題,一般情況下需要對電力系統進行線性化分析。Heffron等[4]提出Philips-Heffron模型,被廣泛應用于電力系統的線性化分析。在Philips-Heffron模型的基礎上,Demello等[5]提出同步發電機阻尼轉矩和同步轉矩,從力學角度對電力系統的穩定性進行了分析。此外,Demello等[5]還研究了勵磁系統對電力系統阻尼轉矩和同步轉矩的影響,證明高增益勵磁系統可能會導致電力系統阻尼轉矩變負,使電力系統不穩定。當然,不只是勵磁系統,調速系統同樣會對電力系統的阻尼轉矩產生影響。王官宏、陶向宇等[6]在Philips-Heffron模型的基礎上加入調速系統模型,分析調速系統對電力系統阻尼轉矩的影響,證明當調速系統對轉速偏差輸入造成的角度偏差為-90°~90°時,調速系統提供正阻尼,角度偏差為90°~270°時,調速系統提供負阻尼。王官宏、黃興[7]證明調速系統放大倍數在正阻尼區間內增大會增大電力系統的正阻尼,在負阻尼區間內增大會增大電力系統的負阻尼。提升電力系統的穩定性,在本質上是增大電力系統的阻尼轉矩。Demello等[5]研究發現在電壓調節器輸入端疊加合適的反饋信號,能夠增大電力系統的阻尼轉矩。以這一概念為基礎設計的電力系統穩定器,對低頻振蕩有很好的抑制效果。與勵磁系統的電力系統穩定器原理類似,調速系統也有相應的調速側電力系統穩定器。郝玉山等[8]研究調速側電力系統穩定器在單機無窮大系統中的應用,針對調速側電力系統穩定器在調速系統中的疊加點、結構、基本原理進行可行性分析。Chen Yujiao等[9]基于廣域測量信號對調速側電力系統穩定器進行優化設計,其性能優于僅基于本地信號設計的調速側電力系統穩定器。Mayouf等[10]在調速側電力系統穩定器的設計中加入模糊邏輯控制,進一步增強對電力系統低頻振蕩的抑制作用。在單機無窮大系統調速側電力系統穩定器設計理論的基礎上,郝玉山等[11]將調速側電力系統穩定器推廣應用至多機系統。Mayouf等[12]應用遺傳算法對采用模糊邏輯控制的多機調速側電力系統穩定器進行優化設計。
在實際工程中,電力系統除了需要滿足穩定性要求外,電力系統的調節速度還需要滿足一次調頻相關的標準要求。但是,在前述調速側電力系統穩定器設計中,都以電力系統的穩定性為目標,未考慮電力系統的一次調頻性能。筆者在同時考慮電力系統穩定性和一次調頻性能的情況下,對調速側電力系統穩定器進行優化設計,并通過仿真驗證了設計方法的有效性。
2 調速系統對同步電機阻尼的影響
同步電機線性化模型的轉子運動方程為:
(1)
式中:TJ為同步電機慣性時間常數;Δω為轉速角速度增量;ΔTM為機械轉矩增量;ΔTE為電磁轉矩增量;D為阻尼因數;Δδ為功角增量;ω0為額定轉速角速度;s為拉普拉斯變量。
假設調速系統傳遞函數Gg(s)為:
Gg(s)=ΔTM/-Δω
(2)
若只考慮調速系統對同步電機的影響,則同步電機的轉子運動方程可改寫為:
TJsΔω=-Gg(s)Δω
(3)
將s=jωd代入式(3),ωd為電力系統振蕩頻率,可得:
TJsΔω=-HgejφgΔω
=-Hg(cosφg+jsinφg)Δω
(4)
式中:Hg為Gg(s)的幅值;φg為Gg(s)的相角。
同樣,將s=jωd代入式(1),可得:
jωdΔδ=ω0Δω
(5)
將式(5)代入式(4),可得:
TJsΔω=-HgΔωcosφg+HgΔδ(ωd/ω0)sinφg
=-DgΔω+KgΔδ
(6)
ω0=2πf0
(7)
Dg=Hgcosφg
(8)
Kg=Hg(ωd/ω0)sinφg
(9)
式中:f0為電網額定頻率;Dg為調速系統附加阻尼轉矩因數;Kg為調速系統附加同步轉矩因數。
由式(6)可知,當-90°<φg<90°時,Dg>0,此時調速系統提供正阻尼;當90°<φg<270°時,Dg<0,此時調速系統提供負阻尼。
3 電力系統穩定性和同步電機一次調頻性能
根據Q/GDW 1404—2015《國家電網安全穩定計算技術規范》[13]提出的穩定性要求,在正常方式下,電力系統中區域間振蕩模式及與大機組相關的局部振蕩模式在小擾動情況下的最低阻尼比ξ應不小于0.03。
除此之外,Q/GDW 669—2011《火力發電機組一次調頻試驗導則》[14]對火力發電機一次調頻性能提出以下要求:機組參與一次調頻的響應時間trd應短于3 s,機組參與一次調頻的穩定時間tst應短于1 min,對于機組一次調頻的負荷響應速度,燃煤機組達到75%目標負荷的時間t75應不長于15 s,達到90%目標負荷的時間t90應不長于30 s。
綜上所述,電力系統應滿足以下約束:
(10)
4 調速側電力系統穩定器基本原理
由式(6)可知,調速系統附加阻尼轉矩的大小與調速系統傳遞函數Gg(s)的相角φg有直接關系。因此,可以通過附加反控制信號改變φg,改善調速系統的阻尼特性,從而達到抑制振蕩的效果。
包含調速側電力系統穩定器的單機無窮大系統控制框圖如圖1所示。
加入調速側電力系統穩定器后,式(3)需要修正為:
TJsΔω=-[1+Ggpss(s)]Gg(s)Δω
(11)
式中:Ggpss(s)為調速側電力系統穩定器傳遞函數。
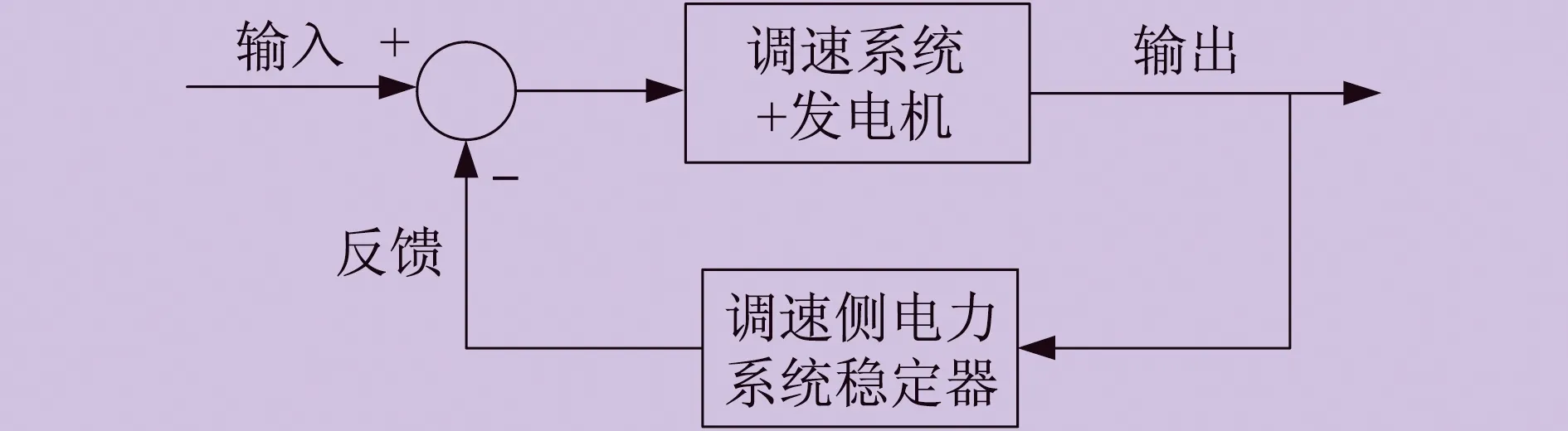
圖1 單機無窮大系統控制框圖
仿照式(3)~式(6)過程對式(11)進行變換,得到:
TJsΔω=-HgΔωcosφg+HgΔδ(ωd/ω0)sinφg
-HgpssHgΔωcos(φgpss+φg)
+HgpssHgΔδ(ωd/ω0)sin(φgpss+φg)
=-D′gΔω+K′gΔδ
(12)
D′g=Hgcosφg+HgpssHgcos(φgpss+φg)
(13)
K′g=Hg(ωd/ω0)sinφg+HgpssHg(ωd/ω0)
sin(φgpss+φg)
(14)
式中:Hgpss為Ggpss(s)的幅值;φgpss為Ggpss(s)的相角;D′g為修正后調速系統的附加阻尼轉矩因數;K′g為修正后調速系統的附加同步轉矩因數。
對比式(6)和式(12),可知調速側電力系統穩定器的加入為同步電機提供了額外轉矩增量ΔTMgpss,為:
ΔTMgpss=-HgpssHgΔωcos(φgpss+φg)
+HgpssHgΔδ(ωd/ω0)
sin(φgpss+φg)
(15)
額外的阻尼轉矩增量ΔTMDgpss為:
ΔTMDgpss=-HgpssHgΔωcos(φgpss+φg)
(16)
若要調速系統提供正阻尼,D′g應大于0,則調速側電力系統穩定器的Hgpss和φgpss應滿足:
cosφg+Hgpsscos(φgpss+φg)>0
(17)
5 調速側電力系統穩定器優化設計
調速側電力系統穩定器的優化設計分為三步:① 濾波器設計[15],根據所需的信號和系統存在的噪聲頻率設計濾波器;② 調速側電力系統穩定器相角調整,根據系統需要補償的相角設計超前滯后環節參數;③ 調速側電力系統穩定器增益調整,考慮系統穩定性和一次調頻性能要求,選取合適的調速側電力系統穩定器增益。
假設通過上述步驟設計得到調速側電力系統穩定器的傳遞函數為:
Ggpss(s)=KgpssGfil(s)G′gpss(s)
(18)
式中:Kgpss為調速側電力系統穩定器增益;Gfil(s)為帶通濾波器傳遞函數;G′gpss(s)為相角補償環節傳遞函數。
5.1 濾波器設計
通常情況下,調速側電力系統穩定器以同步電機轉速作為輸入量。除此之外,在同步電機穩定運行的情況下,同步電機的轉速等于轉速給定值,此時調速側電力系統穩定器的輸出應為零。
綜合以上分析,濾波器在保留低頻振蕩信號的同時,應具有消除直流分量和高頻噪聲的特性。
濾除直流分量可以通過高通濾波器實現。同時,還應保留頻率在0.2 Hz以上的信號。因此,選擇的高通濾波器傳遞函數Ghighpass(s)為:
(19)
高通濾波器傳遞函數伯德圖如圖2所示。
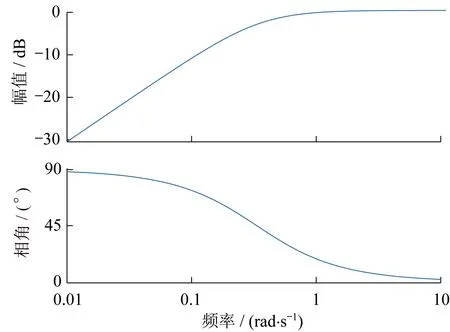
圖2 高通濾波器傳遞函數伯德圖
高通濾波器的截止頻率約為0.053 Hz。
通過低通濾波器濾除2.5 Hz以上的噪聲信號,選擇的低通濾波器傳遞函數Glowpass(s)為:
(20)
低通濾波器傳遞函數伯德圖如圖3所示。
低通濾波器的截止頻率約為3.2 Hz。
將高通濾波器與低通濾波器串聯,組成帶通濾波器,其傳遞函數Gfil(s)為:
(21)
帶通濾波器傳遞函數伯德圖如圖4所示。
帶通濾波器的通帶為0.053~3.2 Hz。
5.2 調速側電力系統穩定器相角調整
由式(15)可知,調速側電力系統穩定器的加入為系統提供了額外轉矩。假設調速側電力系統穩定器只增加系統的阻尼轉矩,由式(15)可知,調速側電力系統穩定器傳遞函數的相角φgpss應滿足:
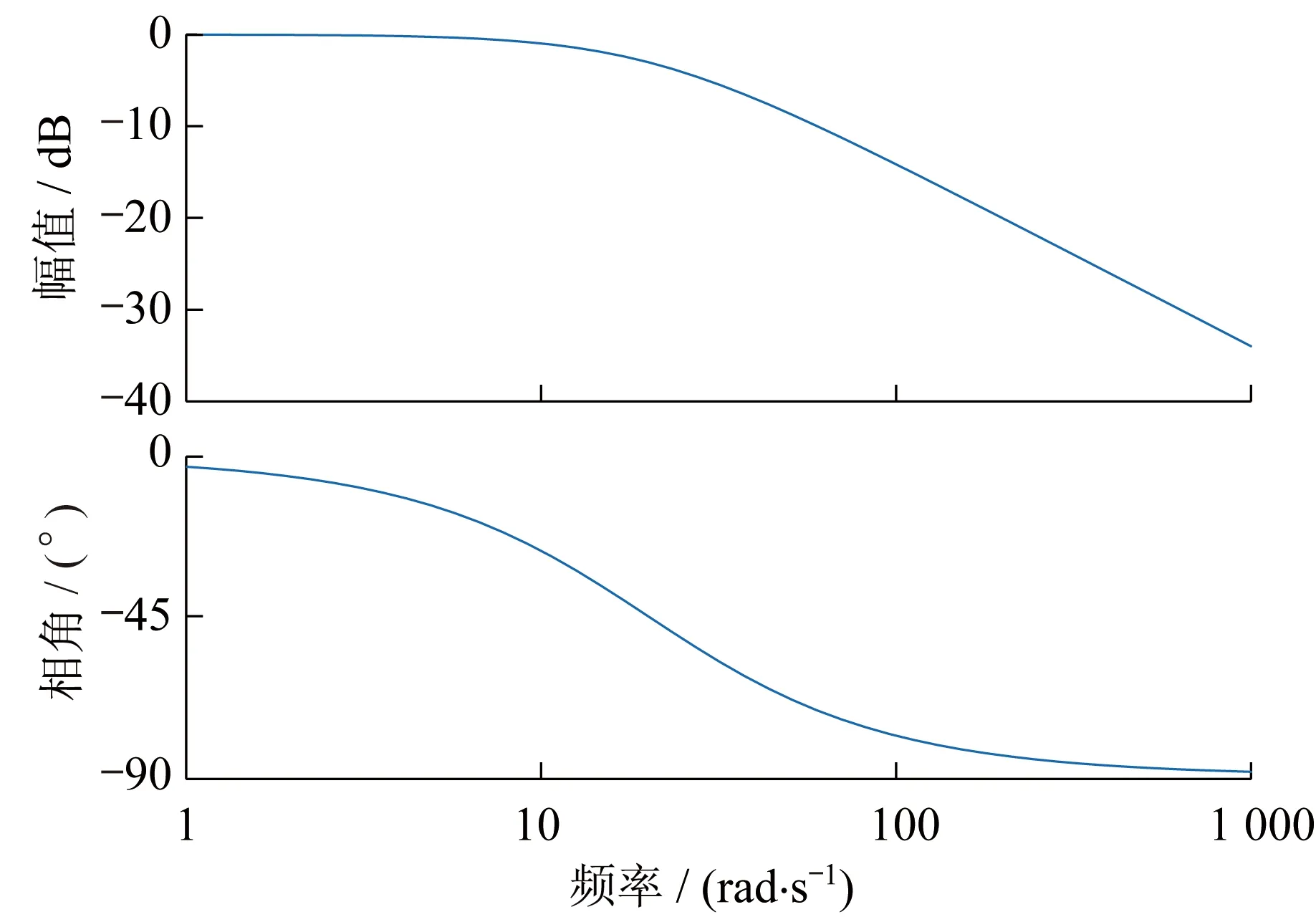
圖3 低通濾波器傳遞函數伯德圖
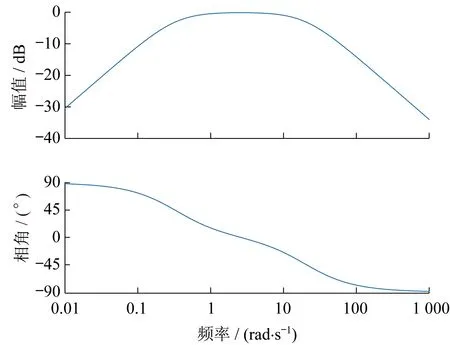
圖4 帶通濾波器傳遞函數伯德圖
φgpss+φg=0
(22)
即:
φgpss=-φg
(23)
φgpss中包含濾波器造成的相角變化φfil和超前滯后環節造成的相角變化φ′gpss。超前滯后環節造成的相角變化φ′gpss為:
φ′gpss=-φg-φfil
(24)
對于n階超前滯后環節,傳遞函數G′gpss(s)為:
(25)
式中:T為調速側電力系統穩定器時間常數;α為調速側電力系統穩定器時間比例常數。
每個環節需要補償的相角θ為:
θ=φ′gpss/n
(26)
求解式(25)中的參數α和T,得:
(27)
(28)
將求解參數代入式(25),得到完整的調速側電力系統穩定器超前滯后環節傳遞函數。
5.3 調速側電力系統穩定器增益調整
由式(16)、式(18)可知,調速側電力系統穩定器的增益Kgpss直接決定調速側電力系統穩定器提供阻尼的大小。若Kgpss取值偏大,有可能導致系統一次調頻性能下降或其它模式增幅振蕩產生。若Kgpss取值偏小,則無法有效抑制低頻振蕩。在同時考慮系統穩定性和一次調頻性能要求的情況下,Kgpss需要滿足相應的約束條件:
(29)
式中:Kmin1、Kmin2、Kmin3、Kmin4、Kmin5為各約束條件對應的Kgpss取值范圍下限;Kmax1、Kmax2、Kmax3、Kmax4、Kmax5為各約束條件對應的Kgpss取值范圍上限。
取交集,將式(29)合并,得到Kgpss的取值范圍為:
(30)
6 算例
筆者以某電廠發電機為例,搭建單機無窮大系統仿真模型,驗證調速側電力系統穩定器優化設計方法的有效性。
濾波器設計已詳細介紹,濾波器的傳遞函數為式(21)。
計算補償相角及補償環節參數。系統特征值見表1。
系統存在頻率為1.351 Hz的負阻尼振蕩模式。需要配置調速側電力系統穩定器的調速系統模型如圖5所示。圖5中,Pcv為調門指令,Pgv為調門開度。
s=jωd=j2π×1.351=j8.49
將s代入式(3)、式(4)、式(21),計算得到:
φg=210.3°
φfil=-20.8°
90°<φg<270°,調速系統提供負阻尼。
將φg、φfil代入式(24),得到需要補償的相角φ′gpss為:
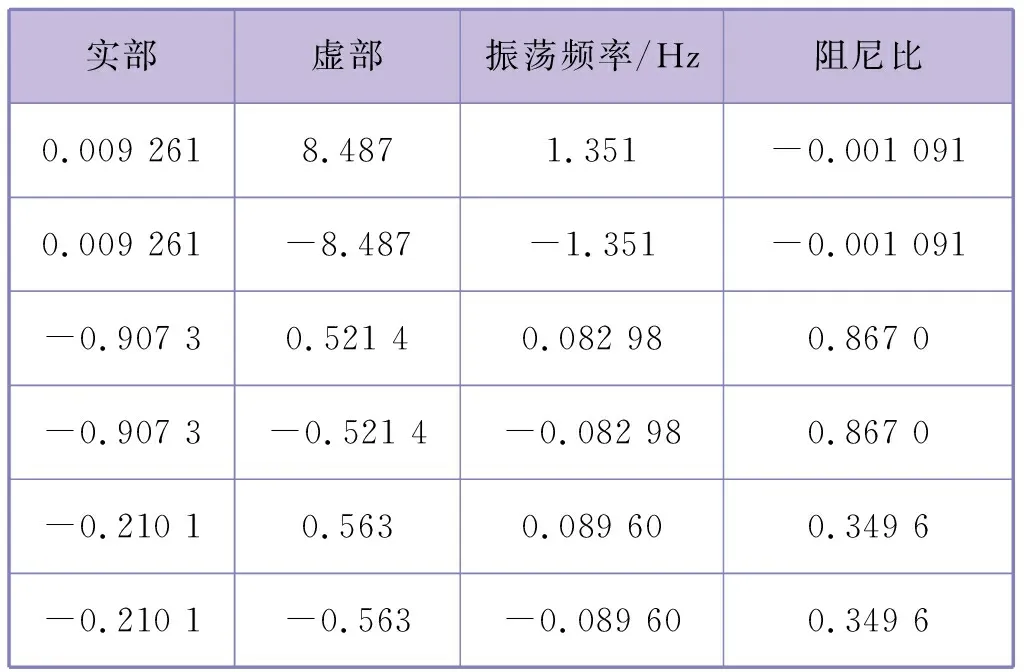
表1 系統特征值
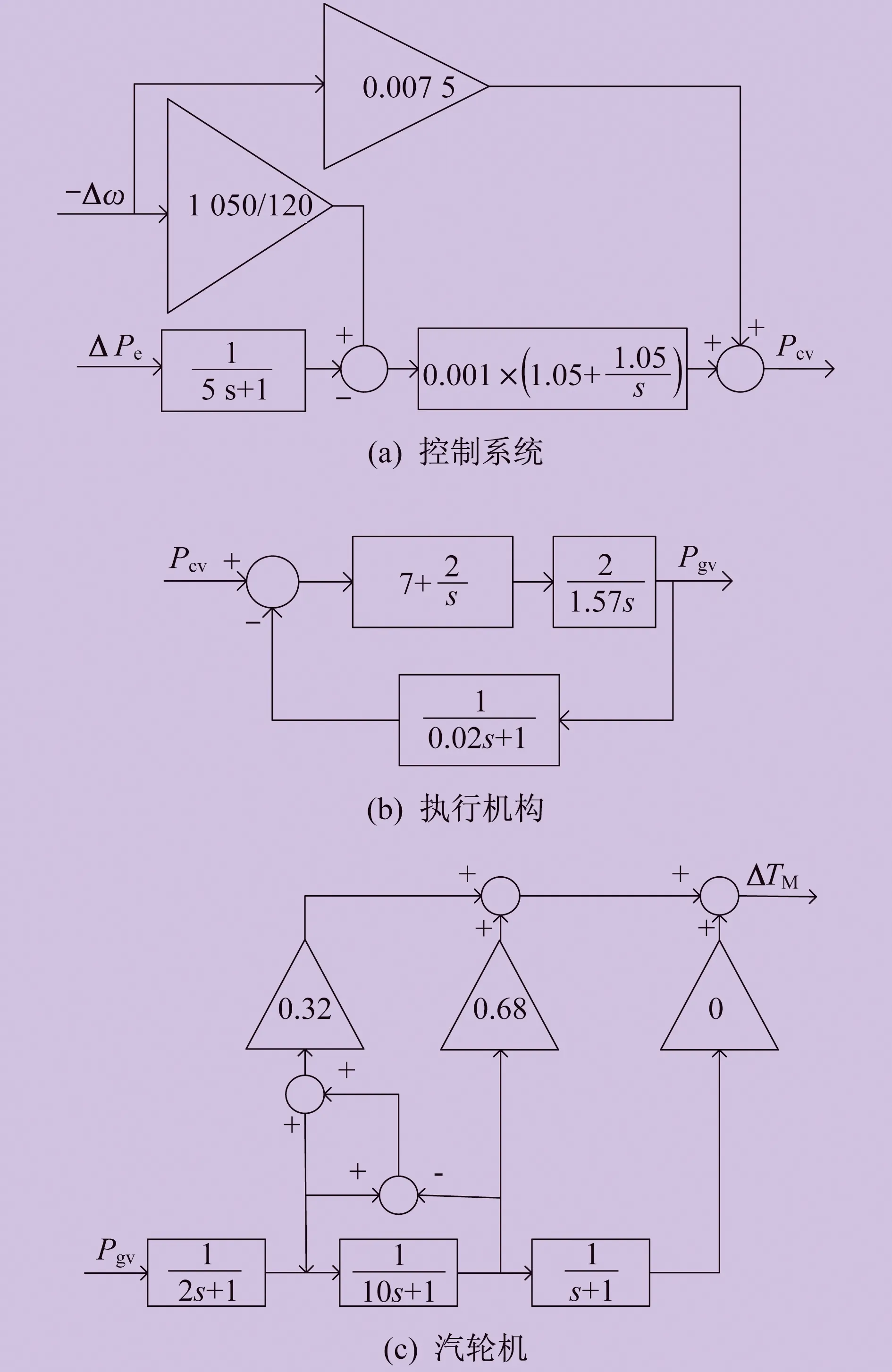
圖5 調速系統模型
φ′gpss=-(210.3°-360°)+20.8°=170.5°
選用三階超前滯后環節進行補償,每個環節需補償的相角θ為:
θ=170.5°/3=56.8°
計算式(25)的參數,得:
由系統根軌跡圖得,在滿足電力系統穩定性要求的情況下,Kgpss應滿足:
0.023 (31) 最后,考慮電力系統一次調頻性能要求對Kgpss的約束。通過仿真試驗的方法,在式(31)的基礎上確定滿足一次調頻性能的Kgpss取值范圍。 發電機一次調頻性能試驗電磁功率偏差標幺值仿真曲線如圖6所示。由圖6可知,在滿足式(31)的情況下,電力系統滿足一次調頻性能要求。 圖6 發電機一次調頻性能試驗電磁功率偏差標幺值仿真曲線 因此,同時滿足電力系統穩定性和一次調頻性能要求的Kgpss取值范圍為式(31)。 筆者對調速系統削弱電力系統阻尼的原理進行了分析。在此基礎上,提出調速側電力系統穩定器的優化設計方法,在滿足電力系統穩定性要求的同時還滿足電力系統一次調頻性能要求。具體優化設計過程為:設計帶通濾波器,使調速側電力系統穩定器只保留低頻振蕩信號;設計相角補償環節,使調速側電力系統穩定器為電力系統提供正阻尼轉矩;選取合適的調速側電力系統穩定器增益,使調速側電力系統穩定器同時滿足電力系統穩定性和一次調頻性能要求。最后通過仿真驗證了優化設計方法的有效性。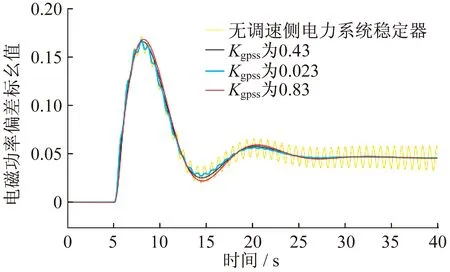
7 結束語

