數(shù)學思維視域下“思維力”的認識與思考
——以逐次漸進思想和極限思想為例

肖 鵬 黃星林

（黔南民族幼兒師范高等專科學校基礎教育系，貴州 都勻 551300）

一、數(shù)學思維

數(shù)學思維是人腦和數(shù)學對象交互作用并按照一般的思維規(guī)律認識數(shù)學規(guī)律和本質的理性活動[1]。廣義上的數(shù)學思維就是指數(shù)學活動中的思維；狹義的數(shù)學思維主要是由數(shù)學問題推動而發(fā)展起來的思維，具有抽象化、形式化和多樣性等特征。數(shù)學思維方法的教育有助于培養(yǎng)學生辯證的思考能力，使學生養(yǎng)成全方位觀察思考問題的習慣[2]，從而創(chuàng)造性地提出解決數(shù)學問題的思維力。

二、逐次漸進思想與極限思想

（一）逐次漸進思想

逐次漸進方法主要是指在解決具體數(shù)學問題中，逐次縮小或擴大研究范圍，把實驗與推導相結合從而用逼近、驗證、淘汰和選擇等簡化問題，化繁為簡、化難為易；從而逐步逼近問題本質，所以逐次漸進方法也叫逐步逼近方法[3]。逐次漸進方法在解決新數(shù)學問題時有得天獨厚的地位，通常新問題的出現(xiàn)，人們面臨的問題主要是缺少方法和缺少理論從而通過摸索式地解決問題，所以她具有利于解決數(shù)學問題，有在數(shù)學理論發(fā)展中起重要作用；從這個角度而言，逐次漸進方法提倡的更多是一種觀念、一種思維方式和進取精神。

（二）極限思想

“極限思想”方法，是數(shù)學分析乃至全部高等數(shù)學必不可少的一種重要方法，也是“數(shù)學分析”與在“初等數(shù)學”的基礎上有承前啟后連貫性的、進一步的思維的發(fā)展[4]。

極限思想也稱為極限思維方法或無限思維方法，是一種無法進行具體體驗的數(shù)學思維，但卻在人類認識客觀世界的歷史進程中發(fā)揮著巨大的作用。研究主要從數(shù)學方法論的角度對極限思想進行解讀，可以說極限思想是數(shù)學發(fā)展不可或缺的工具，也是人們從數(shù)學角度更為深刻地理解客觀事物之間宏觀或微觀的有力武器。極限思維方法的出現(xiàn)對數(shù)學自身的成長起到了巨大推動作用，是數(shù)學發(fā)展史上重要的里程碑，這是數(shù)學思維力量的高光時刻，是數(shù)學思維中暴力美學的極致。學生在領會“極限”時不僅需要了解數(shù)學發(fā)展歷史，而且也要理解數(shù)學思維的變化歷程，并反復認知，才能融會貫通[5]。

（三）逐次漸進思想與極限思想的異同點

數(shù)學史上從來沒有一種思維方法可以絕對獨立存在；也沒有兩種數(shù)學思維像逐次漸進方法與極限思想這樣極其相似又各自大放異彩。逐次漸進思想與極限思想既相互聯(lián)系又相互區(qū)別；逐次漸進思想是極限思想得以產生的實踐基礎和方法論，極限思想是逐次漸進思想結晶，二者的異同點梳理如下：

序號 維度 逐次漸進方法 極限思想 相同屬性1時間 時間跨度大 時間跨度小2空間 一維性 多維性3方向 循環(huán)往復 單向前進4方法 從整體到局部再到整體 無限逼近 恒等轉化5變化速率 量的積累 質的飛躍 逐步逼近6抽象程度 抽象程度低 抽象程度高 無限細分7感知程度 可以進行具體感知 無法進行具體體驗10 對應案例 頻率、割圓術 概率、微積分

序號 維度 逐次漸進方法 極限思想 相同屬性8思維傾向 一種觀念 一種方法9 內涵和外延 內涵小外延大 內涵大外延小10 對應案例 頻率、割圓術 概率、微積分

三、逐次漸進思想與極限思想碰撞的火花

（一）從頻率到伯努利大數(shù)定律

逐次漸進方法為我們探究新的數(shù)學問題提供了全新的理念。例如在研究隨機現(xiàn)象的可能性大小時，實際中我們不可能對每一個事件都做大量的試驗，所以數(shù)學家們才利用逐次漸進的思想從經驗上升到理論，根據規(guī)律總結出事物的本質屬性；于是從頻率的穩(wěn)定性出發(fā)給出了表征事件大小的概率的定義[6]，見表1。

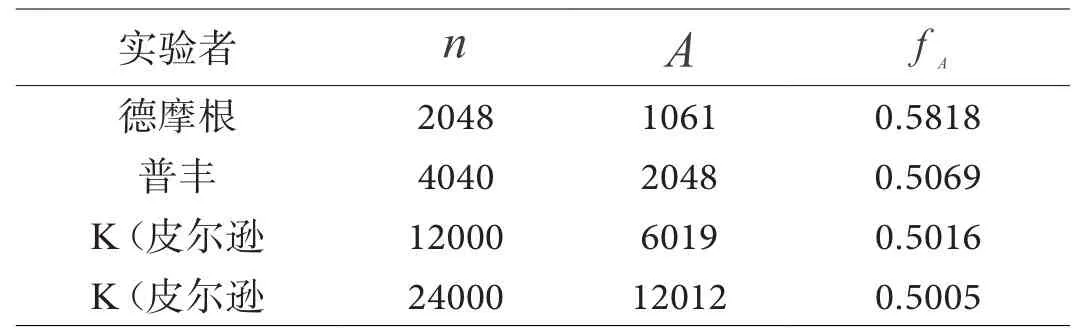
表1 頻率的穩(wěn)定性

這就是著名的投擲硬幣的實驗，由此得出一個概率論中非常重要的設想：“當試驗次數(shù)N逐漸增大時，頻率總是在概率附近波動”。瑞士數(shù)學家雅各布（伯努利（Jakob Bernoulli，1654-1705），概率論的先驅之一，在他的著作《猜度術》一書中論證了這一設想，后人稱之為伯努利大數(shù)定律，如下所示；值得一提的是這本書在他死后8年，即1713年才得以出版。

（二）從“割圓術”到微積分的創(chuàng)立

“割圓術”到微積分是研究中西數(shù)學文化大碰撞的重要文化瑰寶；蘊含了深邃的極限思想。三國時代數(shù)學家劉徽（約公元225年-公元295年）在著作《九章算術注》稱：“割之彌細，所失彌少，割之有割，以至于不可割，則與圓合體，而無所失矣”。正是由于其采用了極限的這種無限逼近的思想方法，才能夠得到無比精確的計算答案，從而為計算圓周率建立了嚴密的理論和完備的算法。動態(tài)的二分演化過程使得劉徽精密而又龐大的計算迅猛加速。

微積分的創(chuàng)立把逐步逼近的思想符號化并加速到抽象的“無窮”；直接引發(fā)了數(shù)學的第二次危機。因為17世紀無窮小量并沒有準確統(tǒng)一的表達形式，數(shù)學家靠著非嚴格論證的數(shù)學想象力，使得微積分在運用上取得了廣泛成效。隨之而來的是微積分如何完備的理論探討，從牛頓直接思維的模糊性到清晰的理論邏輯化，經歷了近兩百年。于是極限作為微積分的理論基礎孕育而生，而極限又以唯物辯證法的哲學觀作為理論基礎。微積分是‘數(shù)學分析法’的開端，是集合論的基礎，使‘實數(shù)論’的研究得以更加的深入。總而言之，微積分的創(chuàng)立開辟了數(shù)學發(fā)展的新紀元，它極大地促進了數(shù)學及其他學科的發(fā)展，滲透到近現(xiàn)代自然科學的各個領域，深刻地改變了人類的物質生活，大大提升了人類探索世界的能力。

四、小結

從隨機試驗的頻率到概率，從中國的割圓術到微積分；逐次漸進思想和極限思想在其中發(fā)揮了巨大的作用，更為重要的是這些理論成果背后的思維力量。對于學生的教育而言，教師在教學過程中要注重思維的培養(yǎng)與正確引導，利用科學、合理的方法全面激活學生的思維意識，也要巧妙“挖坑”讓學生“跳”，時學生在探索過程中自主地發(fā)揮智力與潛能，激發(fā)他們的求知欲，增長他們的創(chuàng)新能力，讓學生的思維在知識的海洋中遨游。在不斷提煉問題本質過程中，引發(fā)學生思維意識和求知欲打開學生思路，體會數(shù)學的邏輯之美，培養(yǎng)學生的分析能力和推理能力，從而提升學生的數(shù)學思維力。為數(shù)學專業(yè)學生更好地立足競爭激烈的社會中，銳意進取，突破極限，創(chuàng)造更多社會價值打牢基礎。