基于Morris篩選法的SWMM參數敏感性分析

張 偉， 張 江， 張 曼

(1.睢寧縣水務局， 江蘇 徐州 221000； 2.徐州市黃河北閘管理處， 江蘇 徐州 221000)

隨著城市化進程的快速推進，城市地區發生內澇的概率越來越大，發生的范圍越來越廣，內澇持續時間及積水深度也越來越長。據調查，2008—2010年在全國349個調查樣本城市中，有289個城市發生了內澇，占比80%。北京2012年7月21號特大洪水，造成受災人口高達160.2萬人，116.4億元直接經濟損失；上海市2013年10月7—8日，受強臺風影響，全市平均降水量高達152.9 mm，造成全市大范圍內澇[1-2]。可見，洪水內澇問題給城市造成了巨大的財產損失和人員傷亡。暴雨管理模型(storm water management model，以下簡稱SWMM)能夠動態模擬城市地區遭遇不同重現期暴雨時內澇發生的時間、地點、范圍，在城市地區內澇管理和控制中起了很大作用[3-4]。

SWMM模擬機理主要是根據地形地貌將研究區分為各個子流域，其徑流模塊將該研究區所發生的降水等進行處理，匯流模塊通過管道、河道、水泵、水閘等進行水量、污染負荷輸送。用戶只需將基礎資料輸入模型，就可以得到各相關斷面的污染工程線及流量過程線。在這一過程中，進行模型的參數率定是非常關鍵的，參數的變化對模擬結果影響非常大，因此有必要對模型參數進行分析，識別出敏感參數和非敏感參數[5-6]。根據參數敏感性分析結果，需要對敏感性參數取精確值，非敏感參數取經驗值即可，這樣既可以提高模型參數取值的效率，又能提高模型的精確度。近年來，隨著SWMM模型用戶的增多，很多學者都對模型的敏感度進行了研究，不同研究方法也得到了不同的結果。本文在前期學者研究成果的基礎上，采用應用最為廣泛的Morris篩選法，以江蘇省徐州市某小區為例，研究SWMM模型的敏感性，為模型率定提供參考。

1 案例研究

1.1 模型建立及參數設置

本次以江蘇省徐州市某成熟小區為研究區域，研究區面積約5 hm2，其中透水面積占40%，不透水面積占60%。根據該研究區地下管線資料，結合該區域地形條件，將該研究區概化為雨水管線70條，檢查井65個，出水口3個。根據管線和檢查井的匯水范圍，基于泰森多邊形法，該研究區概化為69個集水區。該研究區經SWMM模型概化后具體情況見圖1所示。

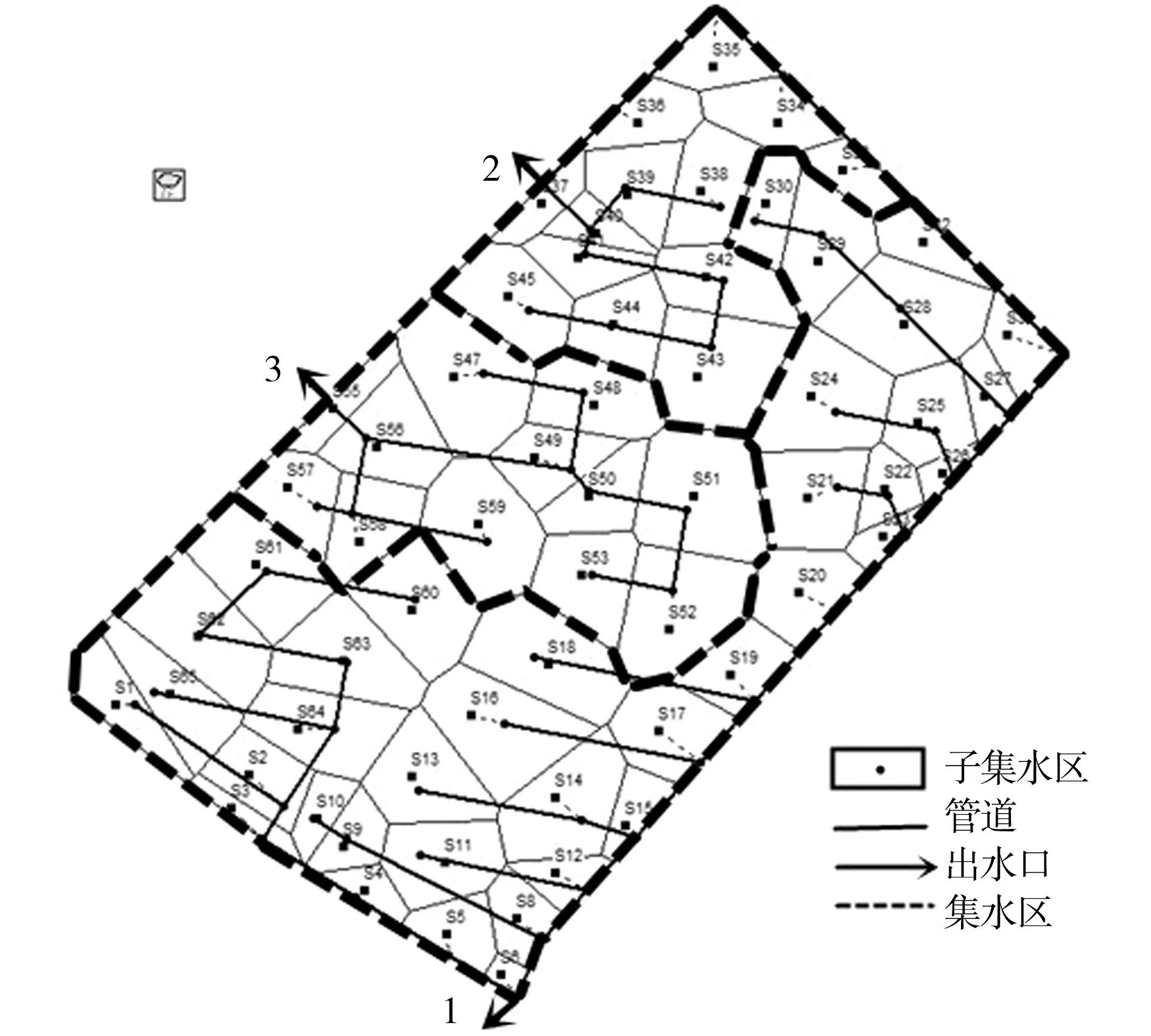
圖1 研究區域概化圖

SWMM模型設置參數的原則如下：

不透水面積：根據研究區土地利用情況確定，可通過實地測量確定準確值；穩定下滲率：查《江蘇省暴雨洪水查算圖表》，并按照徐州市土壤下墊面條件取值；最大下滲率：根據SWMM模型手冊及徐州市土壤類型取值，具體與土壤種類、含水量和植被覆蓋率有關；入滲衰減系數：主要指霍頓曲線入滲衰減系數，具體指土壤浸水達到飽和狀態，到土壤處于干燥狀態所需要的時間，一般取值為2～14 d；滲透性洼地蓄水/不滲透性洼地蓄水：主要指降水的初始損失，即植被截留、洼地蓄水等損失；滲透性/不滲透性粗糙系數：根據SWMM模型手冊取經驗值；坡度：根據徐州市地形資料取值。

SWMM模型中主要參數取值，見表1。

表1 SWMM模型主要參數取值范圍

1.2 設計暴雨過程

研究區的澇水主要來源于降水。綜合考慮徐州市近幾年降雨特性，取暴雨控制時段最大24 h，統計時段選擇1 h、3 h、6 h、12 h、24 h 5個時段。以當地代表雨量站降水資料為基礎，以《江蘇省暴雨洪水圖集》可查的點面折減系數，采用同頻率法可得暴雨時程分配過程，不同重現期的設計雨型見圖2～4。

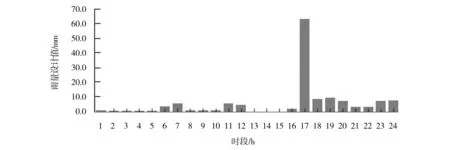
圖2 10年一遇典型暴雨過程

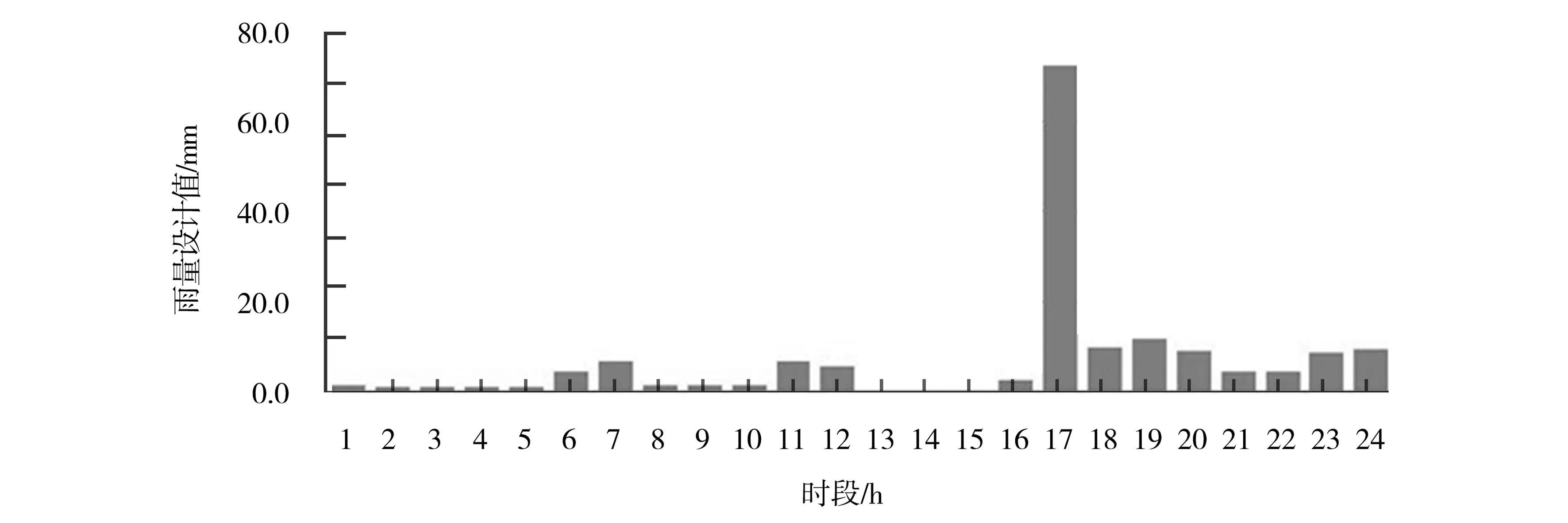
圖3 20年一遇典型暴雨過程

圖4 50年一遇典型暴雨過程

1.3 基于Morris的敏感性分析法

Morris篩選法具體步驟為：(1)從若干個變量中先選定一個變量xi；(2)在變量xi取值上下隨機浮動若干百分比；(3)運用Morris模型得到不同取值xi對應的函數y(x)=y(x1，x2，…，xn)；(4)運用影響值系數ei判斷變量xi取值變化對模型運行結果的影響[7]。

ei=(y*-y)/Δi

(1)

式中：y為變量xi變化之前的運行結果；y*為變量xi變化之后的運行結果；Δi為變量xi的變化幅度。

考慮到Morris篩選法在變量xi取值浮動上的隨機性影響運行結果，本次研究選用修正的Morris篩選法，即變量xi以固定步長百分率改變，敏感性值可取多個Morris系數的平均值，即，

(2)

式中：SN為變量敏感性判別系數；Yi為Morris模型第i次輸出值；Yi+1為Morris模型第i+1次輸出值；Y0為變量按照固定步長百分率調整后模型運行結果；Pi為模型經第i次運行后，變量對于初始變量的變化率；Pi+1為模型經第i+1次運行后，變量對于初始變量的變化率；n為Morris模型的運行次數。

根據變量的SN值，修正的Morris篩選法將參數的敏感性劃分為4種[8]： (1) 若|SN|≥1，則為高敏感參數；(2)若0.2≤|SN|<1，則為敏感參數；(3)若0.05≤|SN|<0.2，則為中等敏感參數；(4)若0≤|SN|<0.05，則為不敏感參數。

本次根據研究區實際情況，選取穩定下滲率、曼寧寬度等11個變量進行敏感性分析，每個參數的固定步長百分率變化值為-30%、-20%、-10%、10%、20%、30%，主要分析研究區遭遇設計暴雨過程10年一遇、20年一遇和50年一遇時，參數對研究區徑流系數和洪峰流量的敏感性。

2 結果分析

根據Morris篩選法，對11個參數按照固定步長改變后，模型運行結果進行分析，分析參數對徑流系數的敏感性，具體分析結果見表2。

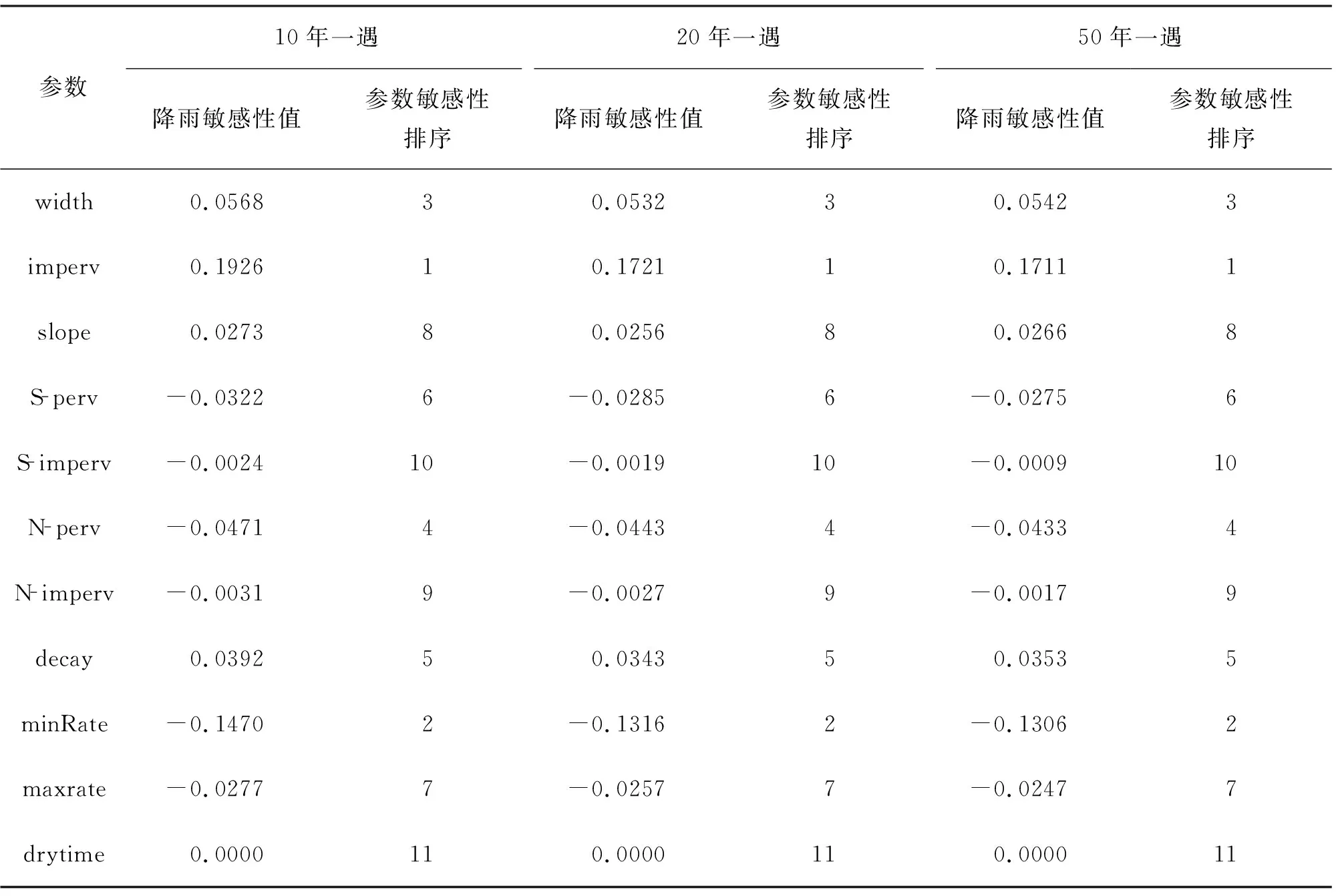
表2 參數的變化對研究區徑流系數的敏感性排序

模型運行結果顯示，對10年一遇、20年一遇、50年一遇3種降雨過程，選取的11個參數敏感性差別較小，但是暴雨設計年限越小，參數的敏感性越高，即10年一遇設計降雨過程參數的敏感性高于20年一遇，20年一遇設計降雨過程參數的敏感性高于50年一遇，3種降雨強度下參數敏感性排序一致。不滲透性敏感性最高，最小滲入速率居第二位，漫流寬度居第三位，三者均是中等敏感度參數，其余8個參數的敏感性較差。

根據Morris篩選法，對11個參數按照固定步長改變后，模型運行結果進行分析，分析參數對洪峰流量的敏感性，具體分析結果見表3。

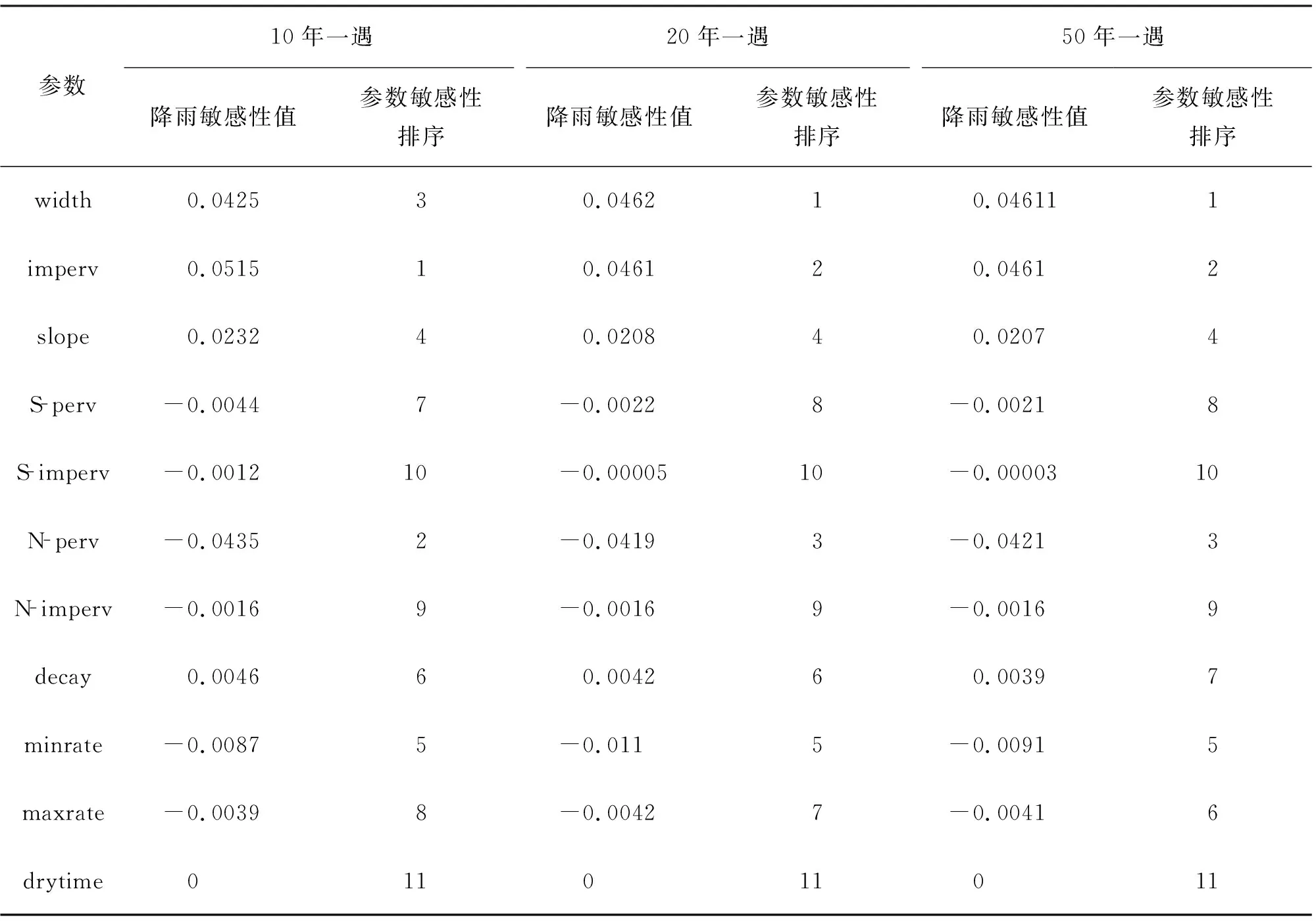
表3 參數的變化對研究區洪峰流量的敏感性排序

模型運行結果顯示，對10年一遇、20年一遇、50年一遇3種降雨過程，選取的11個參數敏感性差別較小，但對不同的設計暴雨過程，參數的敏感性排序有細微差別。10年一遇設計暴雨過程，參數敏感性相對較大的是不滲透性、滲透性粗糙系數、漫流寬度；20年一遇設計暴雨過程，參數敏感性相對較大的是漫流寬度、不滲透性、滲透性粗糙系數；50年一遇設計暴雨過程，參數敏感性相對較大的漫流寬度、不滲透性、滲透性粗糙系數。干燥時間為最不敏感參數，它的變化對洪峰流量完全沒有影響。

3 結 論

本次研究選用修正的Morris篩選法，利用SWMM模型中11個參數的變化對徐州市某小區遭遇10年、20年、50年一遇設計暴雨時，徑流系數及洪峰流量的影響。

(1)不同設計暴雨重現期，11個參數的敏感性排序大體相同；(2)11個參數的變化對徑流系數和洪峰流量的影響不同。其中不滲透性、最小滲入速率、漫流寬度的變化對徑流系數影響較大；漫流寬度、不滲透性、滲透性粗糙系數對洪峰流量影響較大；(3)干燥時間drytime的敏感性最低，取值的變化不會影響模擬結果。