水下航行器基礎運動控制仿真研究?

（海裝上海局駐上海地區(qū)第七軍代室 上海 201108）

1 引言

當前水下無人航行器（Unmanned Underwater Vehicle）在軍用和民用領域飛速發(fā)展，并在工程實踐中發(fā)揮著越來越重要的作用［1，2］。水下無人航行器的驅(qū)動模式主要有舵槳推進操縱、推進器推進操縱、仿生推進操縱等多種形式，其中舵槳操縱具有總體簡潔、阻力性能好、可靠性高等優(yōu)勢，應用最為廣泛［3］。舵槳操縱形式的UUV六自由度空間運動具有典型的耦合性和非線性特征，使其運動控制非常復雜［4～5］。研究UUV的運動仿真技術(shù)、建立UUV的基礎運動控制方法，對UUV的設計和應用具有重要的意義［6］。

文中基于剛體的動量定理和動量矩定理得出的UUV動力學方程，結(jié)合空間運動方程，建立起UUV的六自由度空間運動的數(shù)學模型［7～8］。并針對某小型UUV概念設計階段模型的水動力參數(shù)，基于龍格-庫塔法求解微分方程，編寫相應的六自由度運動仿真程序，實現(xiàn)對UUV空間運動的計算機仿真。采用比例-微分（PD）［9］控制方法對該UUV的速度、艏向、深度這三個基礎運動進行控制［10］。通過對UUV基礎運動控制的研究，可對UUV的操縱性能評估提供參考，還能夠為UUV的路徑規(guī)劃、路徑跟蹤等應用研究提供底層技術(shù)支撐。

2 UUV空間運動方程

2.1 運動方程建立

研究中采用ITTC建議的用以描述水下航行器運動的坐標系［11～12］。固定坐標系O-XYZ，或稱全局坐標系，原點O定在水面或水中一固定點，OX軸一般水平指向北方；OZ軸豎直指向地心，OY與OX軸和OZ軸構(gòu)成右手系。運動坐標系o-xyz，或稱局部坐標系，為非慣性系，坐標原點o固定航行器上某一點，ox軸指向艏正前方；oz軸垂直ox軸指向底部；oy軸與ox軸、oz軸構(gòu)成右手系。本研究中，運動坐標系原點設在UUV浮心位置，固定坐標系原點在UUV運動的初始位置。

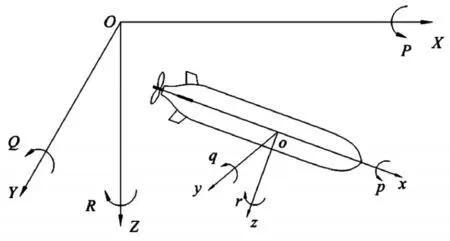
圖1 水下航行器坐標系

在運動坐標系原點位于固定坐標系原點時，將固定坐標系進行旋轉(zhuǎn)變換可與運動坐標系重合，變換矩陣和變換方法如下。

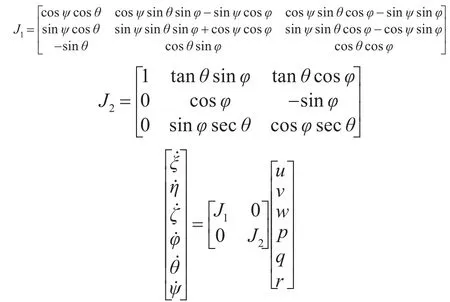
根據(jù)動量定理和動量矩定理導出水下航行器的動力學方程：

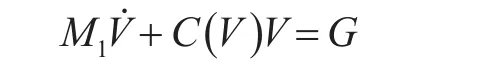
式中，M1為航行器的廣義質(zhì)量矩陣，C(V)為航行器自身的科氏力和向心力矩陣。

2.2 水下航行器受力

2.2.1 靜力

水下航行器受靜力作用包括自身的重力與浮力作用。本文中在坐標原點，因此靜力（矩）GP可表示為

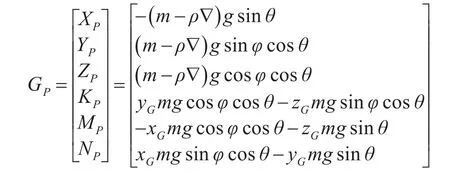
式中，?為水下航行器的排水體積，ρ為流體密度。

2.2.2 水動力

水下航行器所受水動力包括慣性類水動力和粘性類水動力。

對于魚雷形UUV，左右對稱，上下對稱，附加質(zhì)量矩陣如下。

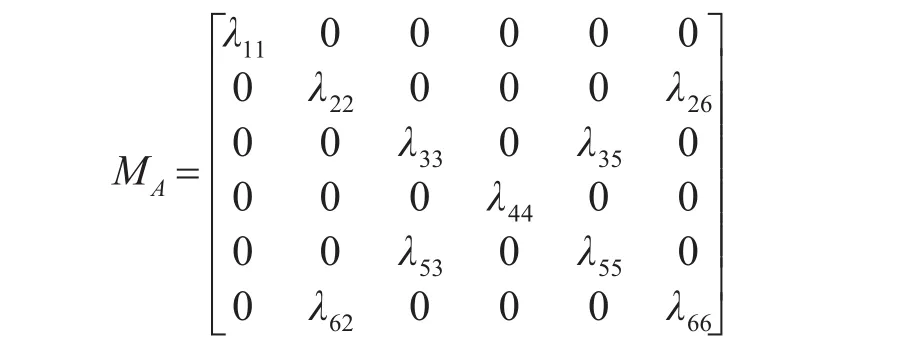
與附加質(zhì)量相關(guān)的慣性類水動力（矩）GA，表達式如下。

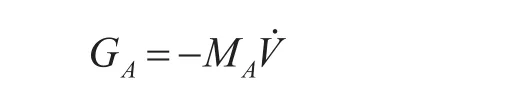
結(jié)合水下航行器的外形特征，可將粘性水動力（矩）GV寫成下列形式。

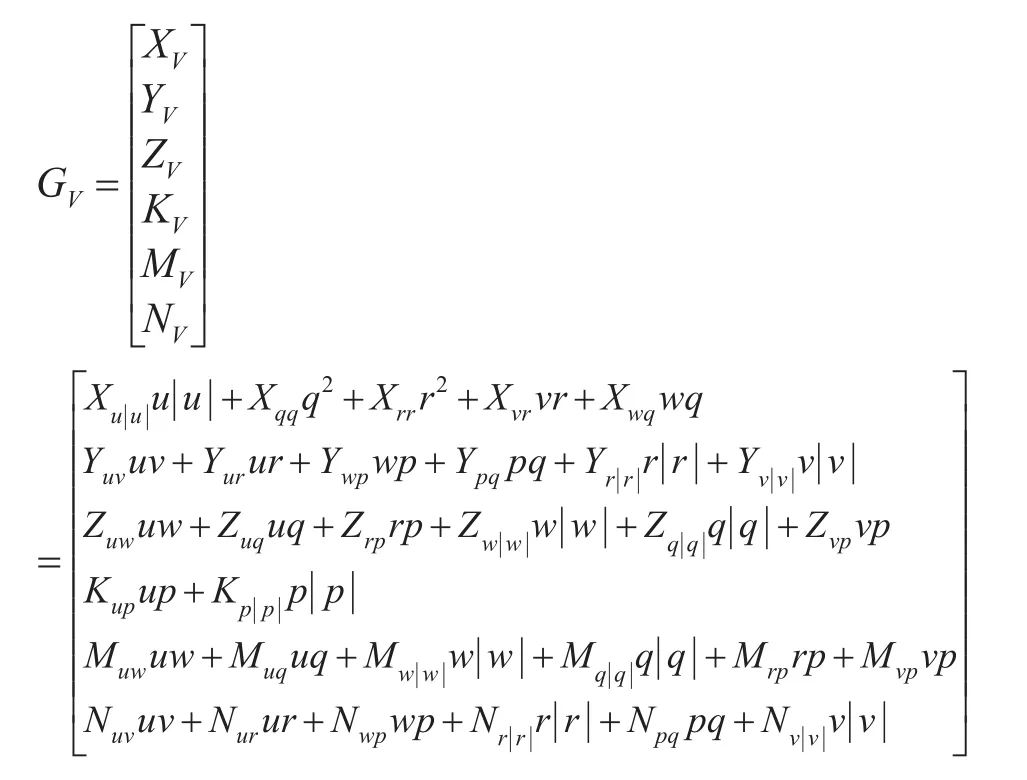
2.2.3 控制力

針對舵槳操縱的水下航行器，其控制機構(gòu)主要是舵和槳，控制力是舵的力和槳的力。

水下航行器的操縱舵可視為小展弦比的機翼，且通常為對稱翼型。舵在流體中受升力和阻力的作用，升力和阻力的大小與流速和舵升（阻）力系數(shù)相關(guān)。

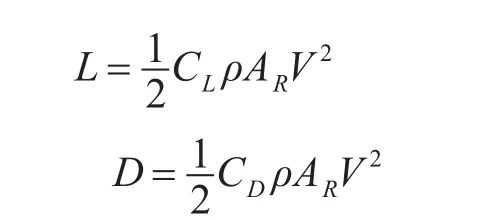
式中，CL和CD分別是舵的升力系數(shù)和阻力系數(shù)，與舵角相關(guān)，AR是舵面積。

舵的作用可表示為

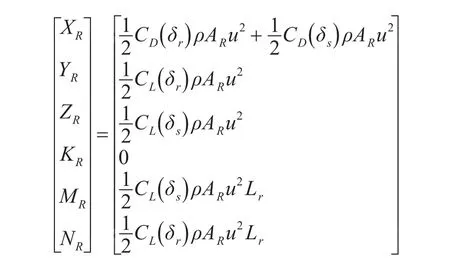
式中，Lr是舵軸距動系坐標原點的距離。

考慮螺旋槳的推力系數(shù)、轉(zhuǎn)矩系數(shù)與無因次量進速系數(shù)相關(guān)，進速系數(shù)又由螺旋槳進速、轉(zhuǎn)速和直徑確定，因此將螺旋槳推力和扭矩的作用以轉(zhuǎn)速、進速的函數(shù)來表示。結(jié)合螺旋槳敞水曲線的特點，采用二次多項式簡化的擬合推力系數(shù)曲線和轉(zhuǎn)矩系數(shù)曲線。若有伴流分數(shù)w和推力減額分數(shù)t的值，也可以帶入槳的計算式中。螺旋槳作用力的最終表達式可寫成：

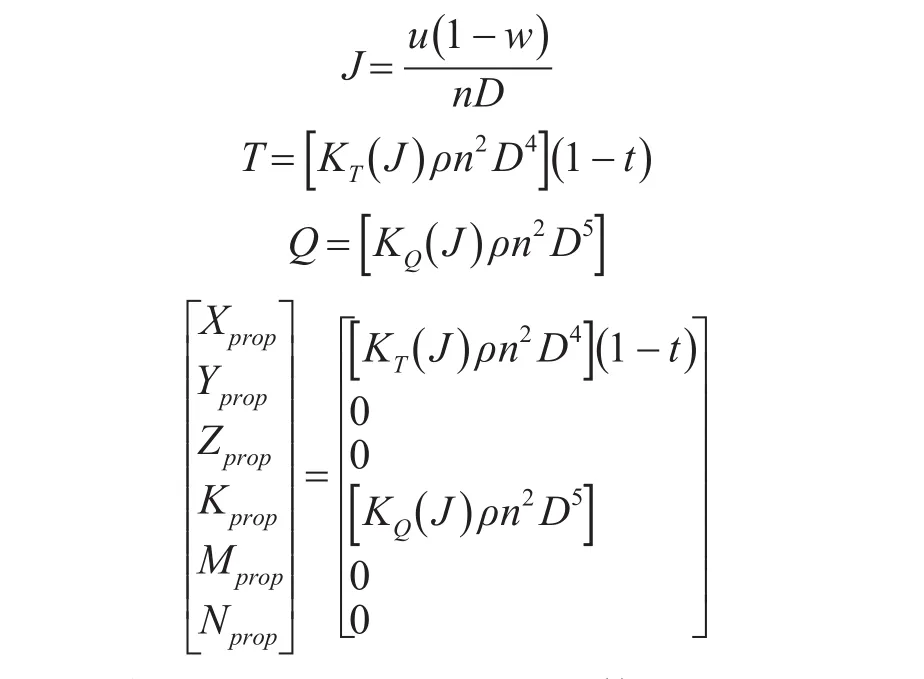
最終，UUV動力學方程可具體的寫成以下的形式。

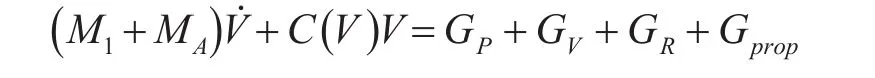
3 運動仿真

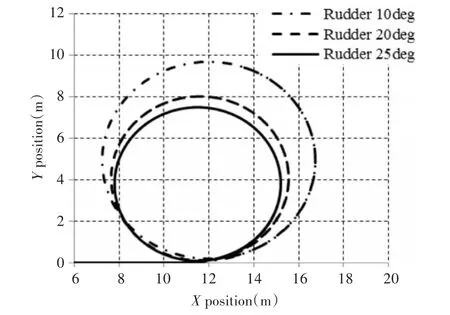
圖2 UUV回轉(zhuǎn)軌跡曲線

基于以上建立的UUV運動方程，采用四階龍格—庫塔法求解偏微分方程，編制UUV六自由度空間運動仿真程序。本文研究的UUV模型，長1350mm，直徑188mm，重30kg。UUV尾部配備一只直徑150mm的常規(guī)螺旋槳，尾部收縮段安裝兩片水平舵和兩片垂直舵。

采用仿真程序?qū)σ?m/s速度直航的UUV進行回轉(zhuǎn)操舵運動進行預報舵角分別為10deg、20deg、25deg。

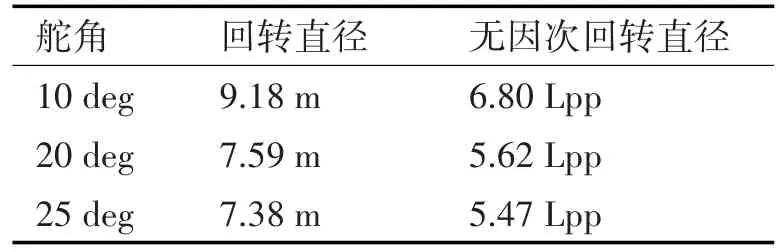
表1 航行器回轉(zhuǎn)直徑

水平面軌跡仿真曲線直觀的仿真出了航行器回轉(zhuǎn)航行的軌跡，并通過軌跡點坐標計算出回轉(zhuǎn)直徑。

4 UUV基礎運動控制

4.1 定速控制

采用PD控制算法對UUV螺旋槳轉(zhuǎn)速進行控制，分別設定UUV前向目標航速0.5m/s，1m/s，1.5m/s，仿真得到的UUV前向航速和螺旋槳轉(zhuǎn)速變化曲線如下所示。

圖3 UUV航速變化曲線

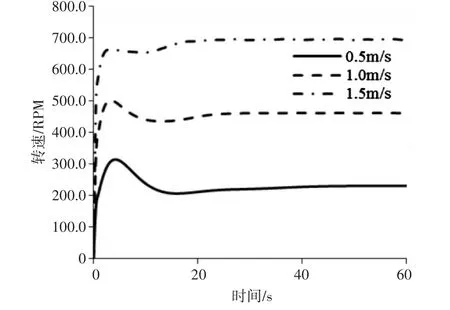
圖4 螺旋槳轉(zhuǎn)速變化曲線

從UUV航速變化曲線可以看出，采用本文中的PD算法，UUV航速在20s左右達到穩(wěn)定，誤差在2%以內(nèi)。

4.2 艏向控制

設定初始狀態(tài)UUV以1m/s速度保持直航，采用PD算法對垂直舵進行控制，使UUV艏向改變30°、60°、90°，仿真得到的UUV艏向角和垂直舵角變化曲線如下所示。

圖5 UUV艏向變化曲線

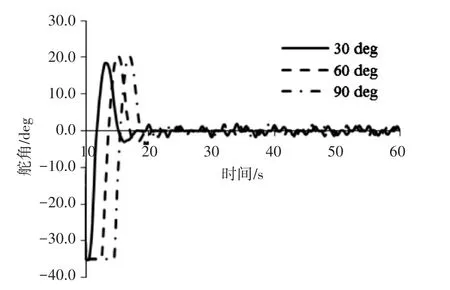
圖6 UUV垂直舵舵角變化曲線

從UUV艏向和垂直舵舵角變化曲線可以看出，采用本文PD控制算法，在最大舵角35deg限制條件下，UUV在達到目標艏向后，經(jīng)過7s左右即能穩(wěn)定在目標艏向角。

4.3 深度控制

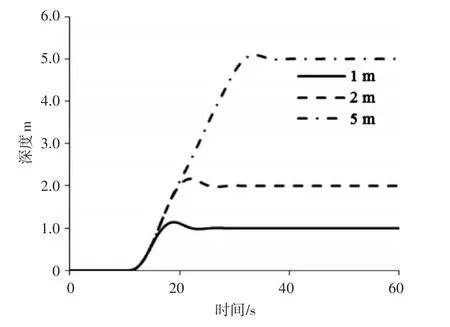
圖7 UUV深度變化曲線

設定初始狀態(tài)UUV以1m/s速度保持直航，采用PD算法對水平舵進行控制，使UUV深度改變1m、2m、5m，仿真得到的UUV深度和水平舵角變化曲線如下所示。

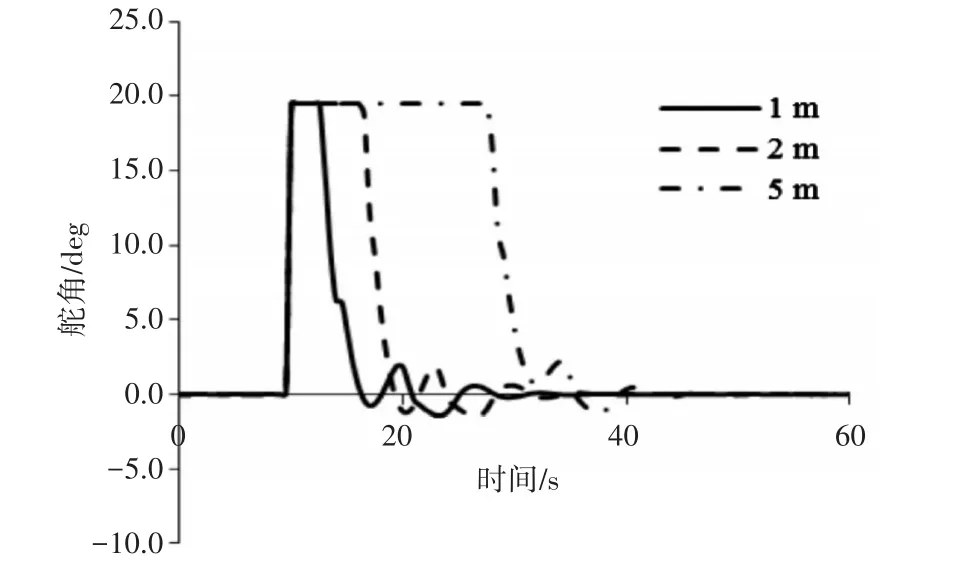
圖8 UUV水平舵舵角變化曲線

從UUV艏向和水平舵舵角變化曲線可以看出，采用本文控制算法，在最大舵角20deg限制條件下，UUV在達到目標深度后，經(jīng)過5s左右即能穩(wěn)定在目標深度。

5 結(jié)語

通過對水下航行器運動和受力的分析，建立了水下航行器的動力學方程，編寫了完善的水下航行器運仿真程序。基于建立的水下航行器運動仿真程序，結(jié)合某小型UUV的水動力系數(shù)建立數(shù)學模型，對UUV的運動進行仿真。通過UUV回轉(zhuǎn)試驗驗證了程序的可行性。基于PD算法，分別對UUV航速、艏向、深度控制進行了數(shù)值模擬，得到相應運動仿真結(jié)果，實現(xiàn)了UUV基礎運動控制目的。

水下航行器運動仿真程序的建立，為研究水下航行器運動控制提供了有效的研究工具。結(jié)合仿真程序，能夠在計算機中實現(xiàn)對控制算法的效果仿真、評估，并能通過仿真效果對控制算法進行針對性的修改。