代價敏感的KPCA-Stacking不均衡數據分類算法*

曹婷婷，張忠林

(蘭州交通大學電子與信息工程學院，甘肅 蘭州 730070)

1 引言

不均衡數據大規模存在現實生活中且在許多領域有著重要應用，如醫療健康診斷、信用欺詐和 入侵檢測[1 - 3]等。通常人們更加關注的是診斷異常或者錯誤的數據，對于不均衡數據分類問題，少數類的錯分代價相對較大，傳統的分類方法旨在最大化整體分類準確率，給研究帶來了一定的挑戰。

國內外學者對不均衡數據分類問題的研究主要從數據層面和算法層面2個大的方面展開。數據層面主要以欠采樣、過采樣、人工合成采樣、混合采樣以及相應的改進算法作為研究點，其主要思想是對數據分布進行重構，使數據達到基本均衡狀態，如SMOTE(Synthetic Minority Oversampling TEchnique)[4]、Borderline-SMOTE[5]等。算法層面一般集中在集成學習、代價敏感學習CSL(Cost Sensitive Learning)[6]和元學習方面。集成學習主要包括Bagging、Boosting和Stacking算法。代價敏感學習CSL的基本思想是在非均衡數據分類中正確識別出少數類樣本的價值比正確識別出多數類樣本的價值要高，因此在分類中應賦予樣本不同的損失代價。文獻[7]基于貝葉斯風險最小化原理提出了一種可以將任意分類器算法轉化為代價敏感算法的 MetaCost算法，根據樣本屬于每個類的概率及誤分類代價之積選取分類代價最小的類別作為樣本分類結果，從而達到誤分代價最小。目前，學者們對一些傳統的分類算法，如支持向量機SVM(Support Vector Machine)、決策樹、神經網絡和 AdaBoost 等提出了對應的代價敏感算法[8 - 11]。王莉等人[12]在代價敏感的理論基礎上提出了NIBoost(New Imbalanced Boost) 算法，該算法結合NKSMOTE(New Kernel Synthetic Minority Over-sampling TEchnique)技術，根據分類錯誤率和預測的類標計算權重系數及各樣本新權重，使分類器在訓練過程中更加關注被錯分的樣本。楊浩等人[13]提出了CSD-KNN(Cost Sensitive based on average Distance of K-Nearest Neighbor)算法，在降低決策邊界樣本密度的重采樣方法的基礎上，以每類樣本的平均距離作為分類結果的標準，使其符合貝葉斯決策理論從而具有代價敏感性，最后按不同的K值以整體誤分代價最小為原則進行Boosting集成，相較于傳統的KNN(K-Nearest Neighbor)算法，CSD-KNN算法平均誤分代價下降且代價敏感性能更好。Kotsiantis[14]提出了一種代價敏感的Stacking集成模型，用C4.5、KNN、樸素貝葉斯NB(Naive Bayes)作為分類器并將其用于不均衡數據分類。Cao 等人[15]將代價敏感的Logistic回歸作為元分類器，提出了IMCStacking(Inverse Mapping based Cost-sensitive Stacking learning)算法，并將快速有效的特征逆映射技術應用于算法中，最大限度利用Stacking集成期間的交叉驗證過程。

綜上，不均衡數據分類中存在以下問題:(1)傳統的分類算法在實際應用中賦予正類和負類相同的錯分代價；(2)集成算法的研究主要集中在Bagging與Boosting模型上，對Stacking集成算法的研究相對較少；(3)數據往往呈現非線性。針對以上問題，本文從代價敏感與Stacking集成的角度出發，提出了一種代價敏感的KPCA-Stacking(Kernel Principal Component Analysis-Stacking)算法，結合自適應綜合采樣ADASYN(ADAptive SYNthetic sampling)方法，按照貝葉斯風險最小化原理使Stacking集成中的初級分類器具有代價敏感性，同時KPCA能在高維度特征空間對核函數映射數據進行主成分分析，對數據進行降維，在特定條件下彌補了PCA算法線性不可分的不足。在KEEL公共數據集上進行了相關的實驗驗證，結果表明代價敏感的KPCA-Stacking算法取得了較好的分類效果，尤其是對少數類的識別。

2 ADASYN采樣

在SMOTE算法之后，He等人[16]提出了ADASYN自適應綜合采樣方法。SMOTE算法作為一種插值法，對每個少數類樣本合成同數量的樣本，對插值區域未進行限定，可能會導致類別重疊和邊界混淆的問題。ADASYN方法可根據數據分布情況為不同的少數類樣本自適應地生成不同數量的新樣本。按照一定的規則和機制，在比較難分類的區域合成更多的樣本，ADASYN具體步驟如算法1所示。

算法1ADASYN采樣

輸入:訓練樣本集D={(x1,y1),(x2,y2),…,(xm,ym)}，其中xi表示樣本,X={xi|xi∈Rn},yi∈Y={1,0}是標簽類，yi=1表示少數類，yi=0表示多數類，用ms和ml分別表示少數類和多數類樣本的數目，滿足ms≤ml且ms+ml=m。

輸出：采樣后新的訓練集Dnew={(x′1,y1),(x′2,y2),…,(x′n,yn)}。

(1) 定義并計算類不平衡度d=ms/ml,d∈(0,1]。

(2) 生成的少數類樣本總量G為:

G=(ml-ms)×α

其中,α∈[0,1]表示加入新樣本后的不平衡度。當α=1時,G表示少數類與多數類的差值，即合成樣本后數據完全均衡。

(3) 對每個少數類樣本xi，利用歐氏距離找出其K近鄰并計算其比率Ri=Δ/K,i=1,2,…,m,Ri∈(0，1]，其中Δ是xi的K近鄰中屬于多數類的樣本數目。

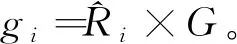
(6) 根據以下步驟為每個少類樣本xi合成gi個樣本：

forj= 1:gi

從xi的K近鄰中隨機選擇一個少數類樣本xzi；

根據線性插值法合成樣本sj=xi+(xzi-xi)×λ，其中λ為隨機數，λ∈[0,1]；

end

3 代價敏感的KPCA-Stacking算法

3.1 Stacking算法思想

集成學習主要包括Bagging、Boosting和Stacking算法，Bagging和Boosting中基學習器一般為同種類型，而Stacking集成是異質的，許多機器學習競賽比如Kaggle中較優秀的解決方案建立在Stacking集成基礎上。Stacking集成算法框架如圖1所示，第1層個體基學習器稱為初級學習器，第2層用于結合的學習器稱為元學習器。Stacking先從初始訓練集中基于各種不同的算法學習出初級學習器，每個初級學習器對原始樣本的預測標記組成新的數據集，將其作為元學習器的輸入特征來訓練一個次級模型。為防止過擬合，使用K折交叉驗證，在構建元學習器訓練集的過程中，可得到測試集數據。

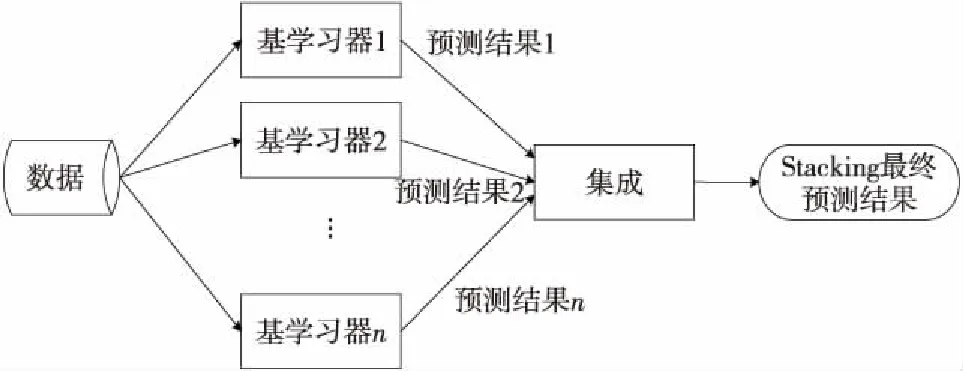
Figure 1 Framework of Stacking integrated algorithm

3.2 代價敏感Stacking算法

基于Staking算法的思想，本文針對現實生活中數據分布存在不均衡性提出了代價敏感的Stacking集成學習算法。選取K近鄰KNN、線性判別分析LDA(Linear Discriminant Analysis)、支持向量機SVM和隨機森林RF(Random Forest)分類器分別按照貝葉斯最小風險化原理改進為代價敏感算法，使用一般最小化分類損失最小化分類錯誤率，代價敏感則以最小化分類代價為目標。最小風險貝葉斯決策理論的主要策略是各種錯誤分類所造成的平均風險最小,通過最小化后驗概率來進行分類決策，一般使用代價矩陣表示分類器的誤分類代價，以二分類為例，首先計算風險，然后再進行決策。

計算風險：

R(yi|x)=∑P(yi|x)Cost(yi,yj)

(1)

決策：

y= argminR(yi|x)

(2)

其中,R(yi|x)為樣本x分類到yi中的風險構造函數，P(yi|x) 為樣本x屬于類別yi的后驗概率，Cost(yi,yj)為類別yi誤分到類別yj的代價。

集成學習效果的好壞主要取決于基分類器的預測精度和基分類器之間的差異性，只有基分類器自身的分類準確率越高并且呈現多樣的趨勢，每個基學習器之間不出現強相關性，集成學習的效果才會越好。如果所有基學習器都產生了相同的預測結果，反而會增加建模的復雜性，所以我們希望不同的基學習器能夠“好而不同”[17]。

考慮到基分類器自身的預測能力，本文Stacking集成的初級學習器選擇自身精度較高且具有差異性的分類器。其中KNN通過測量不同特征值之間的距離進行分類，思想簡單，理論成熟。隨機森林作為Bagging集成框架的代表算法，精度高、抗過擬合能力強，在實際問題中應用廣泛。SVM在高維非線性問題中表現突出。LDA雖常用作降維，但也可作為分類算法。對KNN、LDA、SVM、RF基分類器的性能與相關度分析將在4.3節展開。為了減輕過擬合，第2層分類器最好選擇較為簡單的模型，Stacking框架中邏輯回歸LR(Logistic Regression)或多響應線性回歸MLR(Multi-response Linear Regression)被證明是比較好的方法[18]。本文以傳統統計學方法廣義線性模型GLM(Generalized Linear Model)中應用最廣泛的LR作為Stacking集成的元學習器，LR模型基于概率學理論，模型清晰，簡單易操作且穩定。因此，本文分別將KNN、NB、SVM、RF轉化成代價敏感的算法作為Stacking集成框架的初級學習器，選擇LR作為元學習器，以適用于解決不均衡數據分類問題。

3.3 代價敏感KPCA-Stacking算法

核主成分分析KPCA是非線性降維常用的方法之一，其基本思想是通過核技巧(非線性函數Φ)將m維線性不可分的原始輸入向量空間映射到線性可分的高維空間F，然后在F上進行PCA分析，將維度降到m′，且滿足m>m′，并利用核技巧簡化計算，因此具有很強的非線性處理能力。

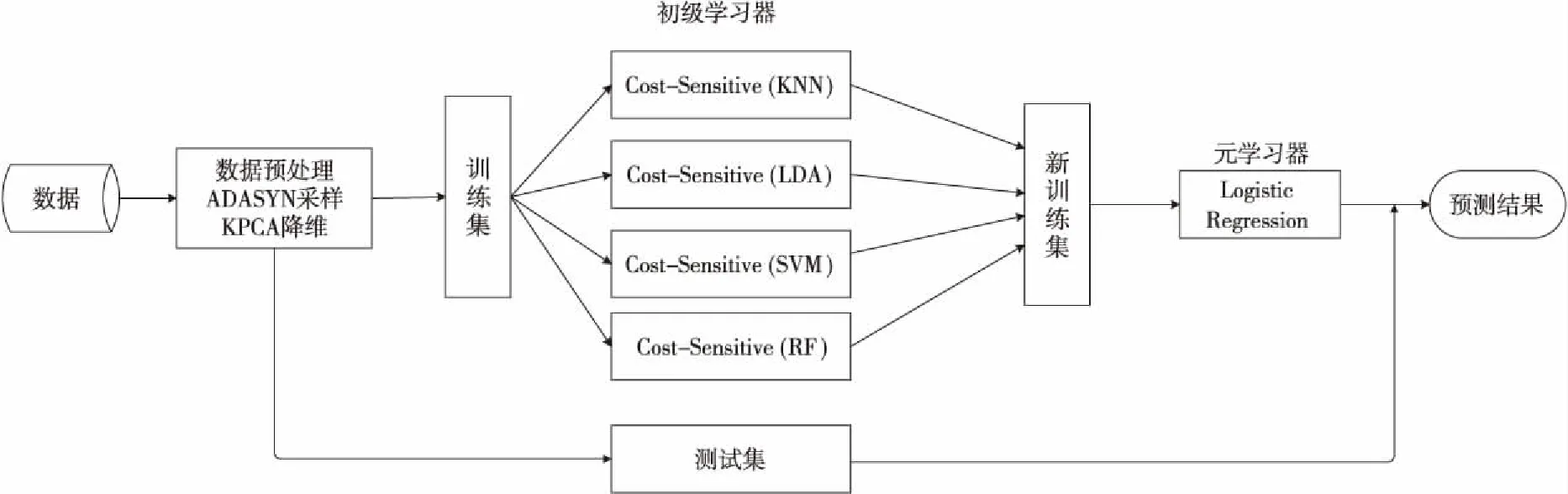
Figure 2 Overall flow chart of cost-sensitive KPCA-Stacking algorithm

將KPCA加入到代價敏感的Stacking學習CSL-Stacking(Cost Sensitive Learning-Stacking)算法框架中，在數據輸入初級學習器之前，對數據特征進行KPCA分析并提取出有效非線性特征，進而提升學習器效果。本文KPCA中的核函數選取徑向基函數RBF(Radial Basis Function)，如式(3)所示：

k(x,xc)=exp(-γ‖x-xc‖2)

(3)

其中,γ=1/(2σ2),σ為徑向基函數的擴展常數。在使用KPCA提取特征之前對數據進行ADASYN采樣。代價敏感的KPCA-Stacking算法的具體步驟如算法2所示，算法整體框架如圖2所示。

算法2代價敏感的KPCA-Stacking算法

輸入：訓練集D={(x1,y1),(x2,y2),…,(xm,ym)}，其中xi∈X,yi∈Y={1,0}，迭代次數T。

輸出：代價敏感的Stacking集成分類器H(x)。

1.采用算法1進行ADASYN采樣;

2.用KPCA進行非線性特征映射，提取有效特征，更新訓練集D′;

3.學習初級分類器;

4.fort=1 toTdo//迭代次數

5. 根據貝葉斯風險最小化原理，將基分類器轉化為代價敏感分類器;

argminR(yi|x) = ∑P(yi|x)Cost(yi,yj)

6.在訓練集D′上學習代價敏感的初級基分類器ht(xi);

7.endfor

8.構建新的數據集;

9.fori=1 tomdo

10.D={(x′1,y1),(x′2,y2),…,(x′m,ym)}/*其中，x′i={h1(xi),h2(xi),…,hT(xi)}*/

11.endfor

12.學習元分類器;

13.在新的數據集Dnew上，學習元分類器Logistic Regression，訓練的模型整體記為H(x)。

14.returnH(x);//組合分類器

4 實驗結果與分析

4.1 數據集

本文選擇類別不均衡的二分類KEEL公共數據集對提出的算法進行分析驗證，若數據集為多類別，則選取其中一種類別作為少數類，合并其他類別作為多數類，數據集的不平衡度IR(Maj/Min)為1.86～8.60，其中，Min和Maj分別為少數類樣本數目和多數類樣本數目。具體信息描述如表1所示。

4.2 評價指標

對于不均衡數據分類而言，準確率并不能提供有用的信息，意義并不大，因此選擇有效的評價指標是非常有必要的。不均衡數據分類模型的評價指標基于混淆矩陣，表2給出了二分類的混淆矩陣。

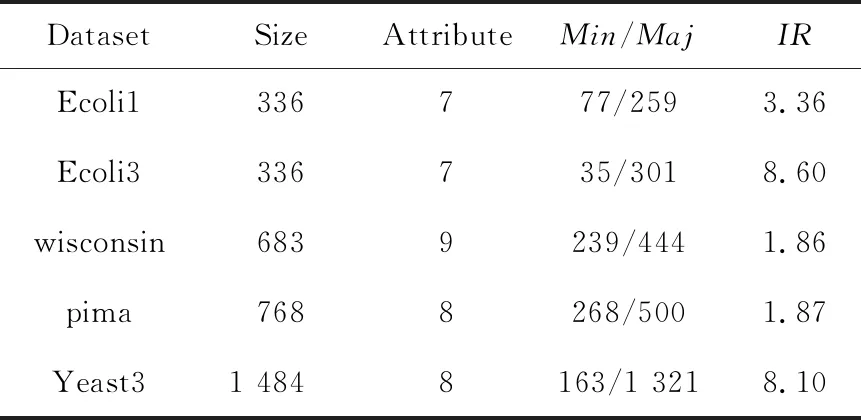
Table 1 Two-class unbalanced data sets

Table 2 Two-class confusion matrix

由于準確率已經不再適用于不均衡數據集，本文選取F-measure、G-mean和AUC作為評價指標，其定義分別如式(4)～式(6)所示。

(4)

其中，查準率Precision=TP/(TP+FP)，召回率Recall=TP/(TP+FN),β一般取值為1，表示Precision和Recall所占比重相同。

(5)

其中，TPR=Recall=TP/(TP+FN),TNR=TN/(TN+FP)。

(6)

其中，FPR=FP/(FP+TN)。

G-mean指標可同時關注2個類上的性能，ROC曲線[19]將FPR作為x軸，TPR作為y軸，因此可以通過ROC曲線評價一個分類器好壞，ROC曲線越靠近左上角，面積越大，AUC值越大，則分類器的性能越好。

4.3 實驗結果及分析

在模型訓練之前，對原始數據進行ADASYN過采樣，采樣前后數據分布如表3所示。

在數據集make_circles上進行PCA與KPCA分析對比，從圖3可以看出，在一個非線性可分的數據集上，經過主成分分析之后，無論如何找到的最大方差的方向數據仍舊是線性不可分的。用基于徑向基函數(RBF)的主成分分析法，將數據集投影到經變換后的特征PC1上可以實現線性劃分，此時只需要PC1一個特征，從而保證了樣本的最佳可分離性。

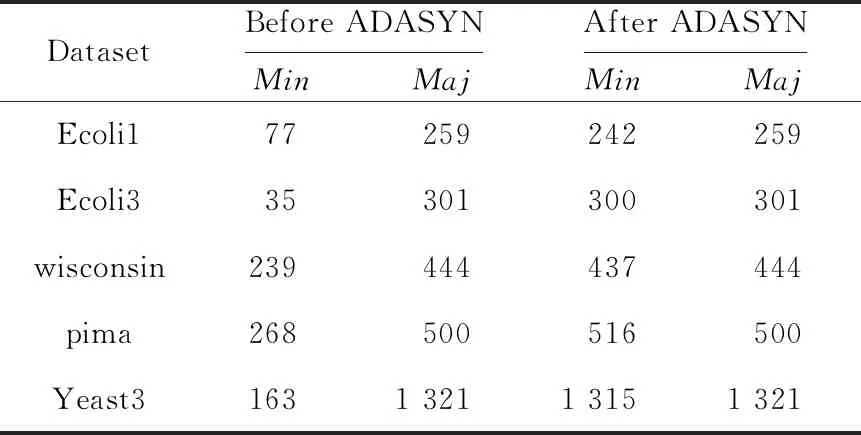
Table 3 Data distribution before and after ADASYN sampling

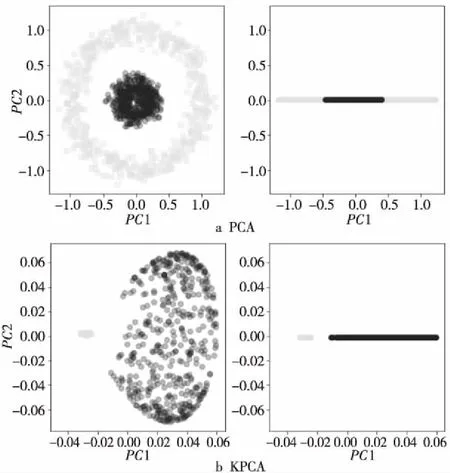
Figure 3 Comparison of the effects of PCA and KPCA on make_circles dataset

為了驗證KPCA能有效提取數據非線性特征，對KPCA-Stacking與Stacking集成框架的初級學習器進行實驗對比。圖4為KPCA-Stacking與Stacking集成框架在數據集Ecoli3上的ROC曲線。ROC曲線下的面積為AUC值，KPCA-Stacking與Stacking的AUC值分別為0.970和0.931。

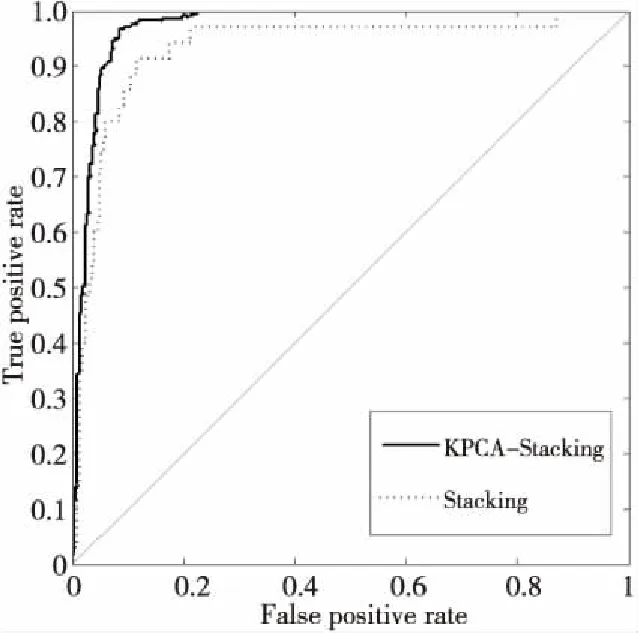
Figure 4 Comparison of ROC curves between KPCA-Stacking and Stacking integrated algorithms

集成學習預測結果優劣的2個決定性因素為基分類器的預測準確率與基分類器的多樣性，在3.2節已經闡述。對于二分類問題，常見的分類器多樣性度量有不和度量(Disagreement Measure)、相關系數(Correlation Coefficient)、Q-統計量(Kappa-Statistic)和K-統計量(Kappa-Statistic)。本文選取相關系數作為度量標準。a和d為分類器Hi和Hj都正確和錯誤分類的樣本數目，c/d分別為分類器Hj/Hi正確分類而分類器Hi/Hj錯誤分類的樣本數目，可得到分類器Hi與Hj的預測結果聯立表，則相關系數ρij定義如式(7)所示。

(7)

相關系數越大，則個體學習器多樣性程度越小。現在KEEL公共數據集上對用于組合學習的初級分類器的性能和相關性進行分析，以確保Stacking集成算法整體性能較優，本文選取數據集wisconsin。

圖5使用點圖可視化了平均估計準確率和95%的置信區間，觀察可知均值以平均準確率降序排序，5個分類器均性能良好，可通過圖5觀察算法的重疊延展性。

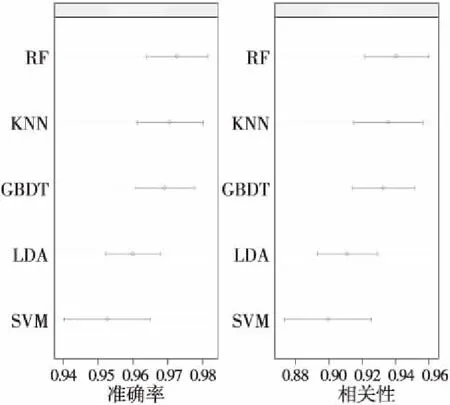
Figure 5 Performance analysis of base classifier

表4給出了各算法之間相關性分析，可看到GBDT(Gradient Boosting Decision Tree)與RF呈現79.9%的較強相關性，且與LDA與KNN相關性也較強，分別為75.2%和76.9%。觀察圖5可知，GBDT與RF與SVM有一定重疊且GBDT比RF分類準確率稍低，因此將KNN、LDA、SVM和RF作為Stacking 集成的較佳組合，保證各算法之間未出現強相關性的同時降低整體算法時間復雜度，為模型集成提供可靠依據。

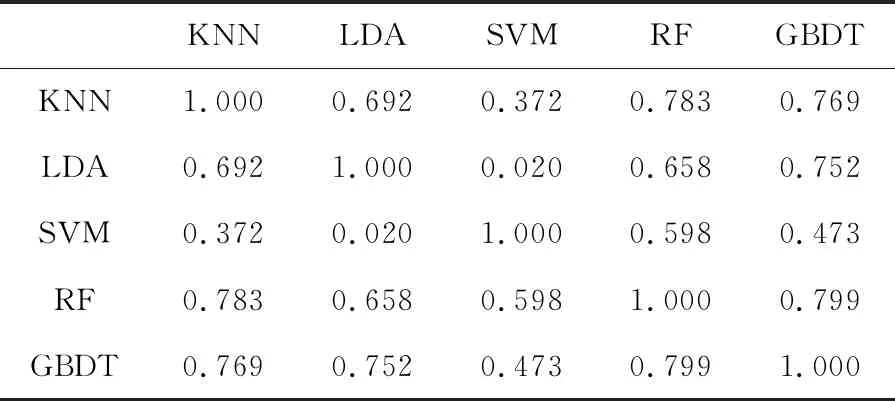
Table 4 Analysis of correlation between different algorithms

首先將代價敏感的Stacking學習算法CSL-Stacking與Stacking集成算法在未經ADASYN過采樣的原始數據集上進行實驗，少數類樣本和多數類樣本在5個數據集上的召回率(Recall)與F-measure分別如表5和圖6所示，相較于Stacking集成學習算法，代價敏感的Stacking學習算法在少數類的識別準確率上有一定提升，證明其解決不均衡數據二分類問題時是有效的。

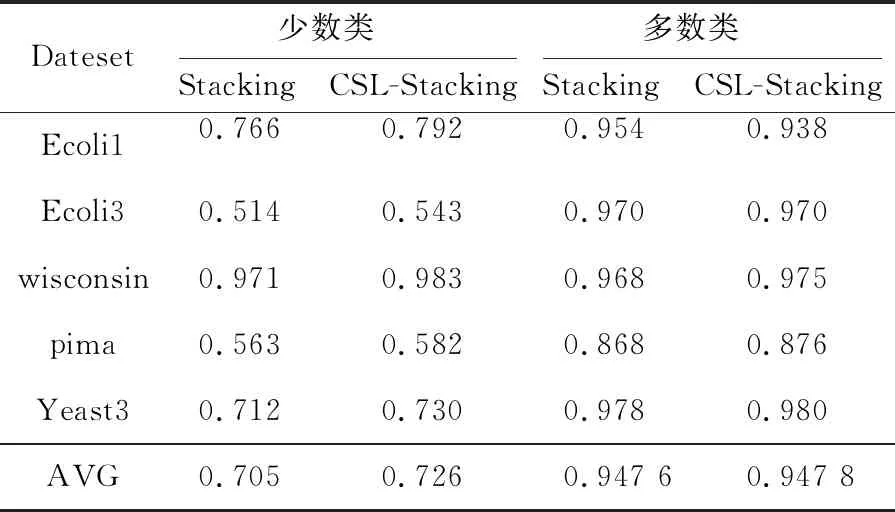
Table 5 Comparison of Recall values between CSL-Stacking and Stacking integration algorithms

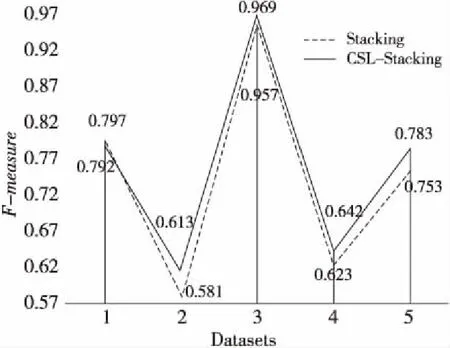
Figure 6 Comparison of F-measure values between CSL-Stacking and Stacking integration algorithms

為了驗證代價敏感的KPCA-Stacking算法在不均衡數據分類上的有效性，將本文算法與其他10種算法進行對比，10種算法包括KNN、LDA、SVM、集成算法RF、C4.5、Bagging、Adaboost、梯度提升樹GBDT和文獻[12]所提出的具有代價敏感性的NIboost算法。其中，NIboost算法采用基于C4.5實現的決策樹(J48)和樸素貝葉斯NB作為Boosting集成的基分類器，分別記為NIboost1和NIboost2。實驗基于Jupyter Notebook和Weka平臺，所有實驗均采用5折交叉驗證，其他參數與文獻[12]均保持一致。分別選取F-measure、G-mean、AUC3個指標進行評價，實驗結果如表6～表8所示，其中AVG列表示該算法的結果在5個數據集上的均值。

分析表6～表8可知，當以G-mean作為評價指標時，文獻[12]的2種算法中基分類器為NB的NIBoost2取得的結果較好，在數據集wisconsin和pima上分別為0.977和0.735，本文代價敏感的KPCA-Stacking算法在數據集Ecoli1、Ecoli3和Yeast3上取得了最好結果，分別為0.912,0.937和0.967。以F-measure作為評價指標時，除了在wisconsin數據集上沒有取得最佳結果，在其他4個數據集上代價敏感的KPCA-Stacking算法均比NIBoost2效果佳。當以AUC作為評價指標時，代價敏感的KPCA-Stacking算法在數據集Ecoli1、Ecoli3和Yeast3上效果最好，相較于整體取得較好結果的NIBoost2算法，分別提升了9.8%，8.0%和12.5%，均值提升了6.72%。在wisconsin和pima數據集上KPCA-Stacking算法效果略微差于LDA。在3個評價指標上代價敏感的KPCA-Stacking算法均取得了最高均值，整體表現良好。

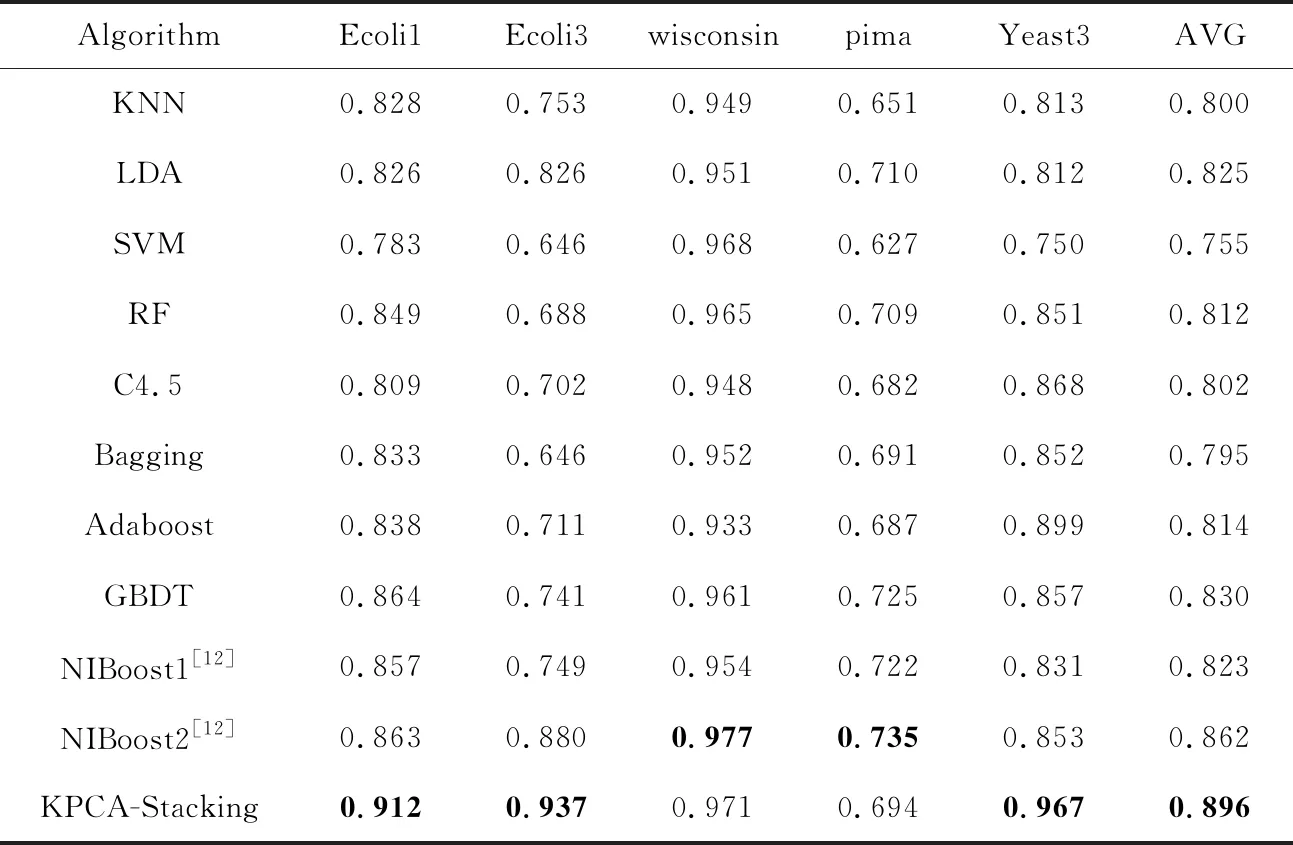
Table 6 Comparison of G-mean of different algorithms on five datasets

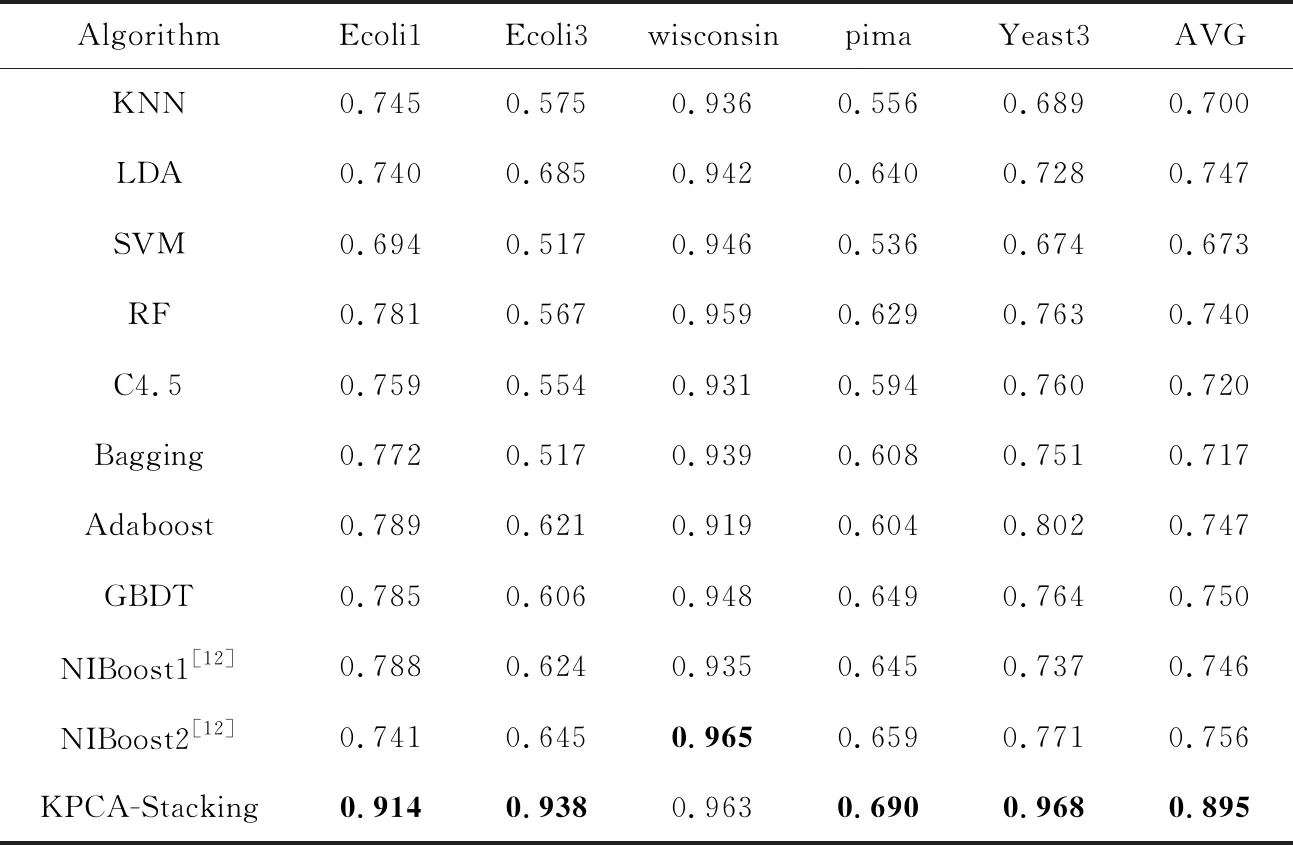
Table 7 Comparison of F-measure of different algorithms on five datasets

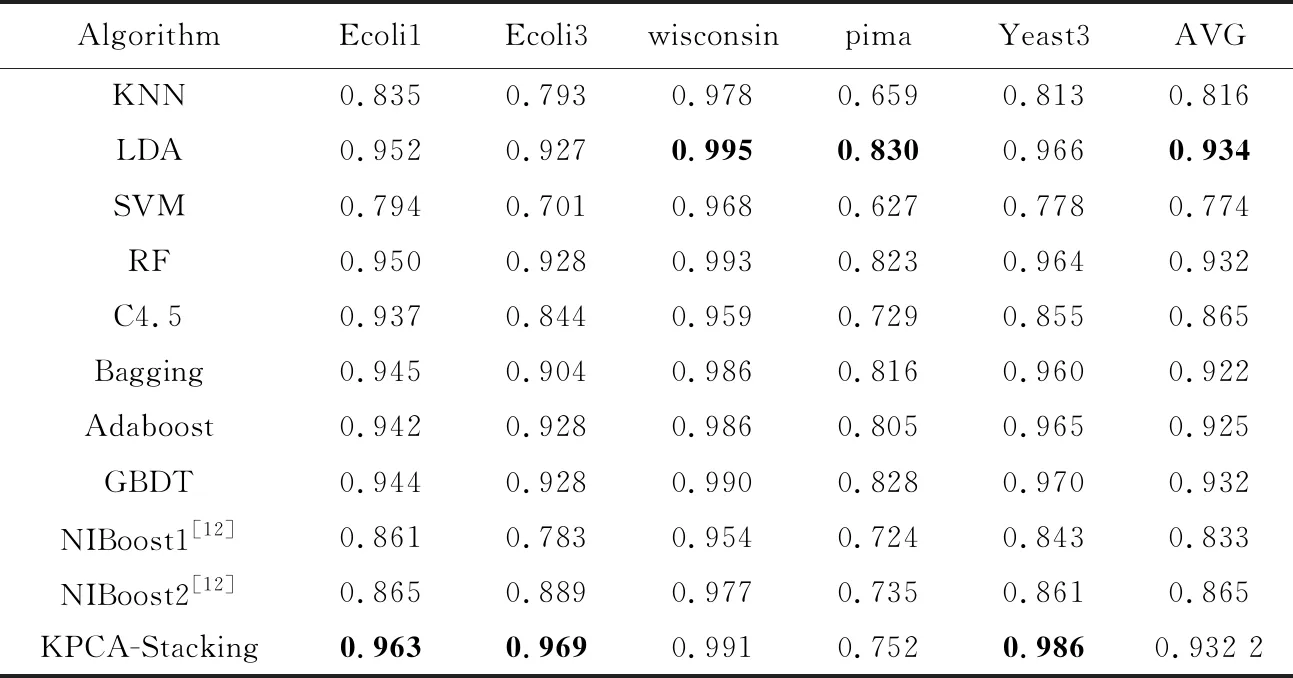
Table 8 Comparison of AUC of different algorithms on five datasets

綜合整體實驗分析可知，單分類器LDA、集成算法RF和GBDT取得了較好的結果，以NB為基分類器的NIBoost2算法效果優于以J48為基分類器的NIBoost1算法，而代價敏感的KPCA- Stacking算法效果優于大部分單個算法和部分集成算法的。因此在不均衡數據分類問題中，基于代價敏感的KPCA-Stacking算法是一種行之有效的方法，在后期研究中可作為一種參考。

5 結束語

本文基于代價敏感思想與KPCA提出了代價敏感的KPCA-Stacking集成算法，使其適用于不均衡數據分類問題。從算法層面入手，將代價敏感的KNN、LDA、SVM和RF作為初級學習器，進一步擴展了初級學習器的范圍，LR作為元學習器，2層架構，KPCA能有效提取數據非線性特征，對數據進行降維。在公共數據集上與J48決策樹等10種算法進行了對比實驗，結果表明，代價敏感的KPCA-Stacking算法在少數類識別準確率上有一定提升，比單個模型的整體分類性能更優，且Stacking模型使用多次交叉驗證算法較穩健，為數據特征非線性與不均衡數據二分類問題提供了新的研究方向。

需要注意的是，本文通過KPCA非線性的方法提取主成分，所提取到的新特征物理意義是不明確的，若要單獨分析某一個或者某幾個因素或特征對分類結果的影響程度，代價敏感的KPCA- Stacking算法則不適用。在適用范圍內進一步提升算法的性能并將其擴展到多分類；Stacking集成策略中尋找弱相關的初級學習器的組合方案；嘗試3層或者更深層的Stacking集成可作為下一步研究的方向。