基于模糊邏輯NSGA-Ⅲ的開關磁阻發電機多目標優化算法*

李藝輝，劉作軍，李 潔

(河北工業大學人工智能與數據科學學院，天津 300132)

1 引言

開關磁阻發電機SRG(Switched Reluctance Generator)因具有結構簡單、堅固，成本低，低速運行性能好，可控參數多，高容錯性等諸多優點，在風力發電[1]、航空航天[2]等領域具有十分廣闊的應用前景[3]。

由于轉矩脈動大、噪聲大等問題，SRG的實際應用受到限制。為解決SRG轉矩脈動較大的問題，國內外學者在SRG本體設計參數[4]、控制參數[5]優化等方面進行了大量研究。在解決SRG轉矩脈動問題的基礎上，為了保證發電機全面高效的運行性能，需對SRG多個性能指標進行優化，因此多目標優化方法的引入對SRG的優化研究具有重要意義[5]。目前，在智能優化算法的研究領域，電機多目標優化方法主要分為傳統多目標優化方法和多目標進化算法[6]。其中，傳統多目標優化方法主要通過評價函數法[7,8]、目標規劃[9]等方法將多目標問題轉化為單目標問題求解。多目標進化算法通過尋優得到一個Pareto解集。基于遺傳算法的多目標優化方法具備遺傳算法較強的全局搜索能力和魯棒性[10]。其中，快速非支配排序遺傳算法NSGA-Ⅱ[11]通過引入擁擠度和精英策略保持了種群的多樣性，提高了電機優化的精度和效率[12,13]，可以高效率處理多目標優化問題，而改善了種群分布的改進NSGA-Ⅱ[14]無法正確估量3目標及3目標以上優化問題的擁擠程度，在優化3個及以上目標的電機優化設計中存在不足。因此，文獻[15,16]提出一種基于參考點的非支配排序遺傳算法NSGA-Ⅲ,以參考點與種群的關聯操作代替NSGA-Ⅱ的擁擠度選擇機制，可從精英策略方面更好地解決包含3～15個優化目標的多目標優化問題。

NSGA-Ⅲ可快速估計多目標優化問題的最優點[15]，但算法本身無法幫助決策者確定滿足自身偏好需求的最優方案。目前，已有研究將后驗偏好信息[13]、交互偏好信息[17]和先驗偏好信息[18]引入多目標優化方法，幫助決策者依據偏好選擇Pareto解集中的最優方案。

本文提出一種基于模糊邏輯NSGA-Ⅲ的SRG多目標優化算法，將偏好信息引入SRG多目標優化。利用RSM對SRG的優化目標進行回歸建模，在保證擬合精度的基礎上，采用基于模糊邏輯NSGA-Ⅲ的SRG多目標優化算法對SRG結構參數和控制參數同時進行優化，即搭建基于模糊邏輯的模糊推理系統，在NSGA-Ⅲ中引入決策者的偏好信息指導NSGA-Ⅲ的尋優方向，通過尋優得到考慮偏好的Pareto最優解集，解集中的各個解附加了相對強度值，決策者選取相對強度值最大的解作為SRG多目標優化的最優方案。

2 SRG初始設計

本文依據SRG設計方法[19]計算得到如表1所示的1 kW四相8/6極SRG樣機的主要設計參數。

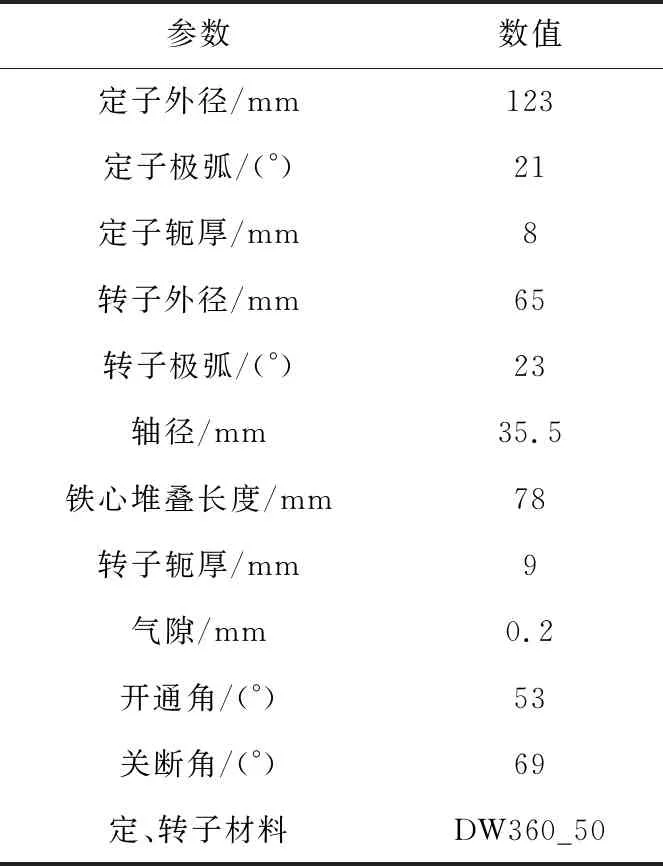
Table 1 Initial design size of four-phase 8/6 pole SRG

利用Ansoft Maxwell軟件對SRG模型進行有限元靜態及瞬態仿真分析，得到恒功率額定工況下SRG的性能，如表2所示。

Table 2 SRG performance under rated conditions

3 SRG優化目標及優化變量

3.1 優化目標及優化變量

通過對SRG的參數化分析，選取對SRG效率、功率密度和轉矩脈動影響較大的參數：定子極弧βs、轉子極弧βr、定子軛厚Ys、轉子軛厚Yr、定子內徑Dsi、開通角θon和導通角θc組成優化變量X，如式(1)所示。

X=[x1x2x3x4x5x6x7]T=

[βsβrYsYrDsiθonθc]T

(1)

將結構參數和控制參數的取值范圍作為優化變量的區間約束條件；此外，考慮到定子極磁密對SRG運行鐵耗的影響，鐵心軛部的結構強度以及發電機運行過程中的溫升和銅耗等因素，將發電機定子極磁密、定子軛部磁密和定子繞組電流密度作為性能約束條件。

為減小SRG轉矩脈動、提高運行效率和功率密度，滿足發電機高效穩定的運行需求，SRG多目標優化問題可表示為：

(2)

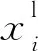
3.2 SRG優化目標的響應面建模

由于SRG的非線性，優化目標η(x)、ρm(x)和KTr(x)無顯式表達，本文采用響應面法RSM(Response Surface Methodology)對SRG優化目標函數進行回歸建模。利用中心復合實驗設計CCD(Central Composite experiment Design)[20]方法進行優化變量的5水平采樣，通過Expert Design軟件得到采樣結果，如表3所示。

待優化因素數目為n，則采用CCD方法進行的總實驗次數為：

m=no+2n+2n

(3)

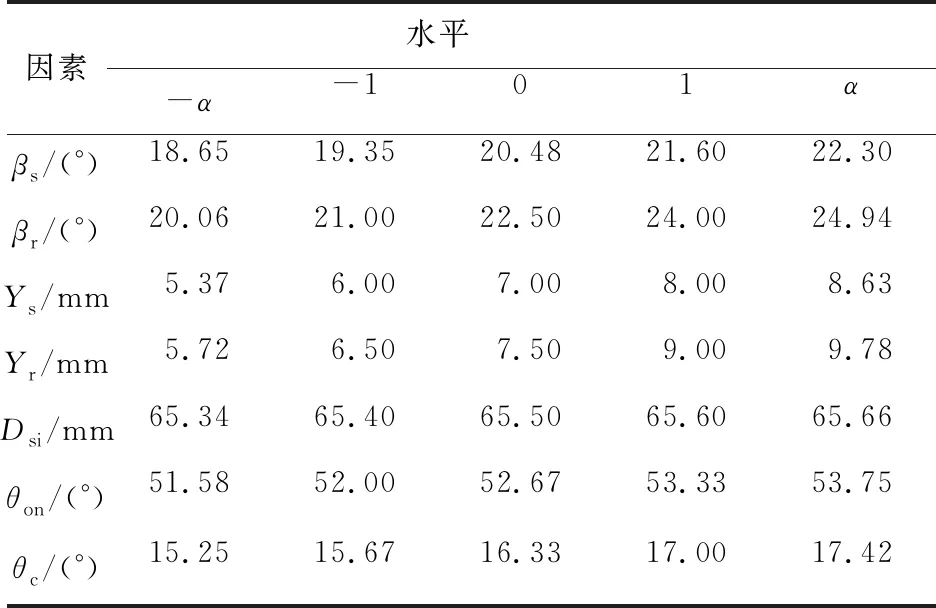
Table 3 Factor and level reference table

其中，no為中心點數目，2n為軸向點數目，2n為析因點數目。本文設置待優化因素數即優化變量數為7，取中心點數目為1，總實驗次數為143次。利用Maxwell軟件對不同水平下的參數組合進行有限元仿真分析得到143組對應響應值，如表4所示。

對表4中的實驗數據進行多元二次回歸擬合，得到SRG優化目標轉矩脈動KTr、發電機效率η和功率密度ρm響應面模型的函數表達分別如式(4)～式(6)所示：

KTr(x)=fKTr(x1,x2,x3,x4,x5,x6,x7)

(4)

η(x)=fη(x1,x2,x3,x4,x5,x6,x7)

(5)

ρm(x)=fρm(x1,x2,x3,x4,x5,x6,x7)

(6)

SRG響應面模型分別如式(7)～式(9)所示。

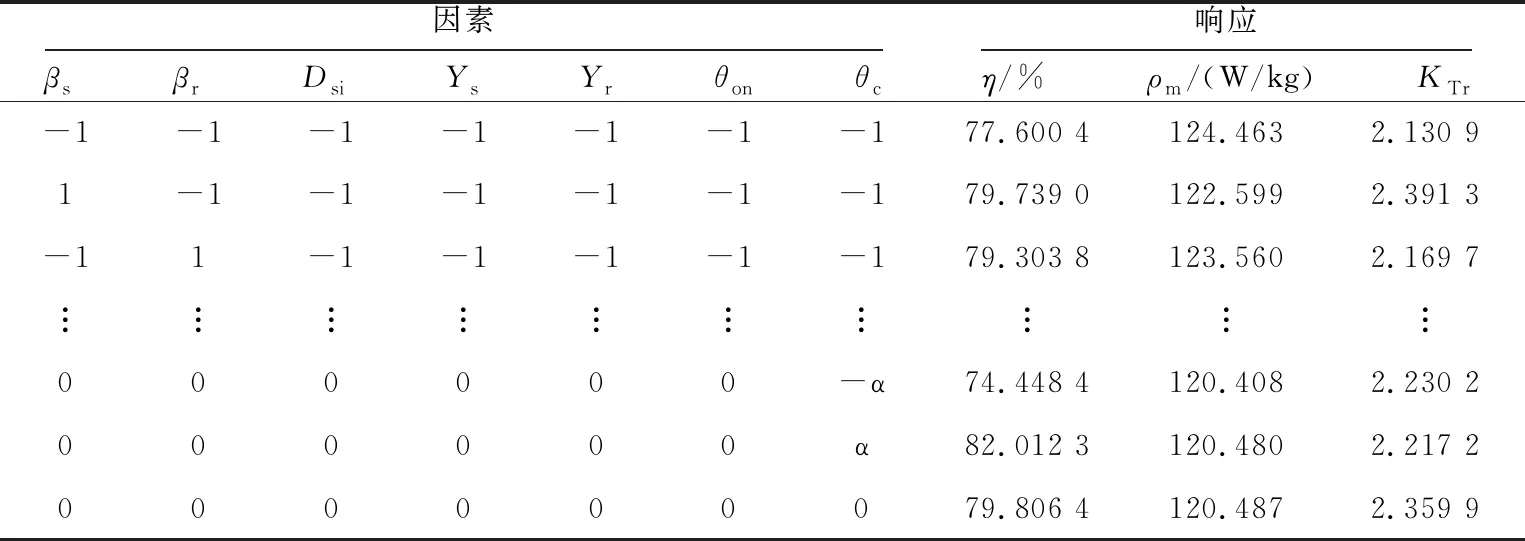
Table 4 Factor and response test data

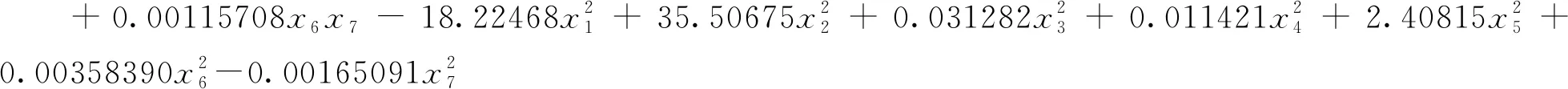
(7)

(8)

ρm(x)=185.17473-31.53661x1-11.11662x2-1.81560x3-0.73350x4-0.42486x5-0.015081x6+0.00626168x7

(9)

SRG優化目標響應面模型(式(3)～式(5))的回歸分析如表5所示。

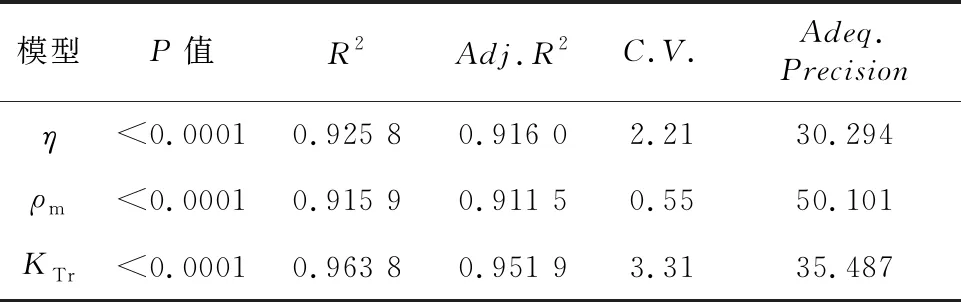
Table 5 SRG optimization target response surface model regression analysis table

有效信號與噪聲比值Adeq.Precision>4，變異系數C.V.<10，響應面模型有較高的可信度和精度；P值(Model Prob>F)均小于0.01，響應面模型顯著，擬合度好，具有高度統計學意義；多元相關系數R2及校正系數Adj.R2均大于0.9，各響應面模型預測精度較高。因此，通過響應面法構造的SRG優化目標模型擬合度好，可信度與精度較高。

4 基于模糊邏輯NSGA-Ⅲ的SRG多目標優化算法

4.1 模糊推理系統

由于決策者對不同優化目標重要程度的判定以及解改進程度的大小無法做出定量的描述，因此本文引入模糊推理系統，建立種群個體間的“強度優于”關系[17]以比較個體的優劣。首先，建立模糊推理系統，通過相對強度值的比較判斷Pareto前沿解之間的優劣，用于指導算法的尋優方向。基于模糊邏輯建立雙輸入、單輸出的Mamdani模糊推理系統，利用模糊語言描述決策者的偏好信息，定量輸出相對強度值Si，如圖1所示。

Figure 1 Fuzzy reasoning system of Mamdani

圖1中優化目標fi(i=1,2,3)的重要性因子Pi由式(10)和式(11)計算得到。

(10)

(11)

其中，cij為優化目標fi對優化目標fj的相對重要程度。本文采用5級標度賦值，并設定3個優化目標的相對重要程度：SRG效率和功率密度同等重要，轉矩脈動比效率、功率密度重要。

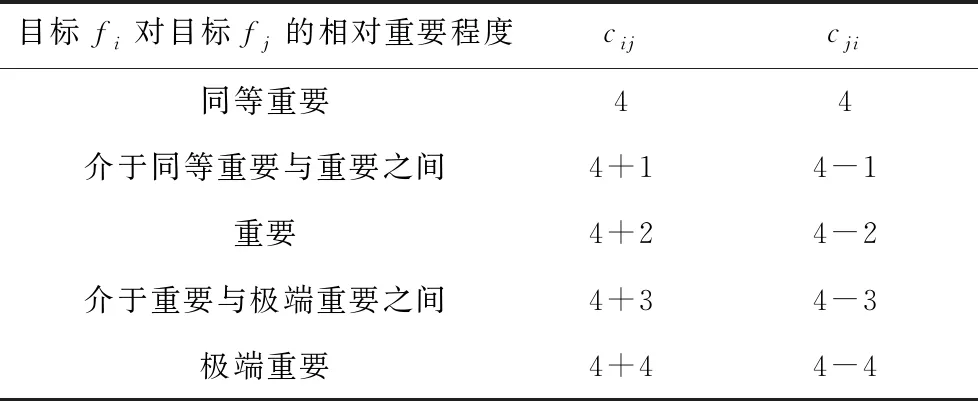
Table 6 5-level scale assignment of relative importance between optimization goals

由表6得到SRG多目標優化中3個優化目標相對重要程度的賦值矩陣C如式(12)所示：

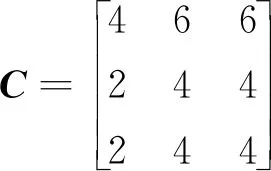
(12)

圖1中Di為2個解x、x′相對于優化目標的改進程度，由式(13)得到：

Di=fi(x′)-fi(x)

(13)

Mamdani模糊推理系統輸出變量Si作為解x對于x′在優化目標fi(i=1,2,3)上的相對強度值，對輸出變量Si采用常用反模糊化方法重心法得到Mamdani模糊推理系統輸出的精確強度值S′。因此，x對優化目標的綜合相對強度值如式(14)所示：

(14)

4.2 模糊邏輯NSGA-Ⅲ算法的主要操作

模糊邏輯NSGA-Ⅲ創建15條模糊規則的雙輸入、單輸出Mamdani模糊推理系統，并預定義一組與種群規模相近的參考點，將種群規模為N的第t代父代種群Pt與經過交叉、變異生成的子代種群Qt合并，對種群數量為2N的合并種群Rt=Pt∪Qt進行相對強度值的比較。同時，對種群個體與參考點進行關聯操作，建立關于種群個體到參考點距離的適應度函數，以保證改進NSGA-Ⅲ的種群多樣性，最終將相對強度值篩選出新的種群數量為N的集合作為新的父代種群。

模糊邏輯NSGA-Ⅲ算法的主要操作：

(1)創建Mamdani模糊推理系統。

依據輸入變量Pi、Di和輸出變量Si的隸屬度函數及規則搭建Mamdani模糊推理系統，設置SRG優化目標相對重要程度的賦值矩陣C以模糊化決策者對于優化目標重要程度的偏好信息。

(2)預定義一組參考點。

采用Deb and Jain方法生成內、外2層參考點，不僅減少了參考點數目，而且還保證了參考點的廣泛分布[16,21]。外層參考點uij由Das and Dennis方法生成。

(15)

其中，M為優化目標的個數；H為歸一化各優化目標坐標軸上平均分成的區域數,uij是集合U1中第i行第j列元素。

基于外層參考點，由式(16)得到內層參考點集U2：

u′ij∈U2

(16)

則(M-1)維超平面上預定義的參考點集U=U1∪U2。

(3)初始化理想點。

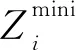
(17)

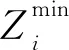
(4)建立適應度函數。

為保證種群個體能夠均勻擴展到整個Pareto搜索域中，基于參考點到種群個體間的距離建立適應度函數，如式(18)所示：

f(x)=(U(x)-Umin+1)×(dmax/d)2

(18)

其中，U(x)和Umin分別為參考點是變量的函數和參考點最小值，d為參考點到種群個體的距離。

模糊邏輯NSGA-Ⅲ算法流程圖如圖2所示。

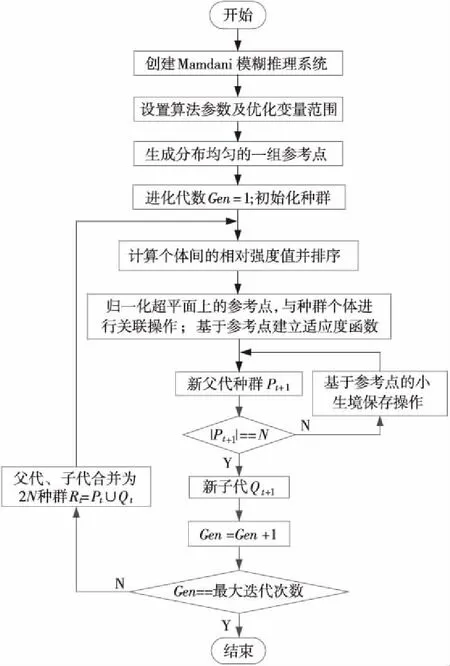
Figure 2 Flowchart of fuzzy logic NSGA-Ⅲ algorithm

5 優化結果及仿真分析

在Matlab軟件中，利用NSGA-Ⅲ和模糊邏輯NSGA-Ⅲ分別優化1 kW四相8/6極SRG的轉矩脈動、效率和功率密度響應面函數，設置種群規模N=200，交叉分布參數ηc=30，變異分布參數ηm=20，最大迭代次數GMax=500。得到Pareto前沿如圖3和圖4所示。

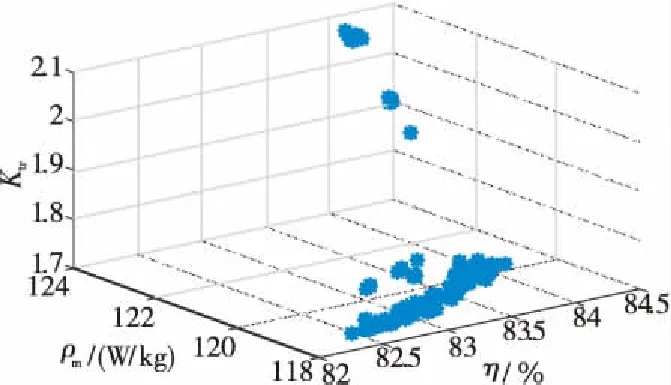
Figure 3 Pareto front after NSGA-Ⅲ optimization

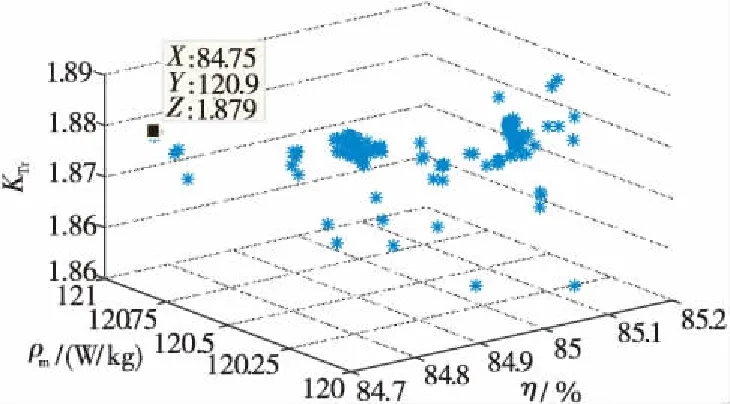
Figure 4 Pareto front after fuzzy logic NSGA-Ⅲ optimization

圖3和圖4中Pareto前沿上所有解的約束違反度為0，均為滿足SRG性能約束的可行解。SRG優化后的模型滿足：KTr<2.0619，η>80.54%，ρm>117.2574 W/kg。圖4中采用模糊邏輯NSGA-Ⅲ優化后的Pareto前沿上解的性能均優于優化前的，且標注點為相對強度值最大的解，即為滿足決策者偏好的最優解。而圖3中采用NSGA-Ⅲ優化后的部分解不完全滿足優化需求，將其剔除，決策者依據偏好從剔除后的Pareto解集中選取最優解，在SRG功率密度約束下，取7組不同效率下的SRG可行解，其分布如圖5所示。

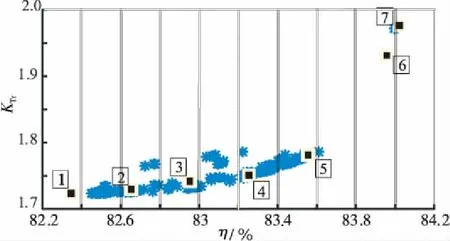
Figure 5 Pareto feasible solution distribution with constraints

圖5的7組優化方案中，方案1轉矩脈動最小，方案7功率密度、發電效率最大。表7和表8為對采用NSGA-Ⅲ和模糊邏輯NSGA-Ⅲ優化后的8組SRG優化方案的分析結果(表7中的θon和θc均為電角度)。

表7列出的8組優化方案的SRG參數組合均從不同程度對SRG的3個優化目標進行了優化，較好地解決了SRG的多目標優化問題，其中方案1～ 方案7為圖5中NSGA-Ⅲ優化后篩選的7組解，方案8為圖4中模糊邏輯NSGA-Ⅲ優化后相對強度值最大的解。

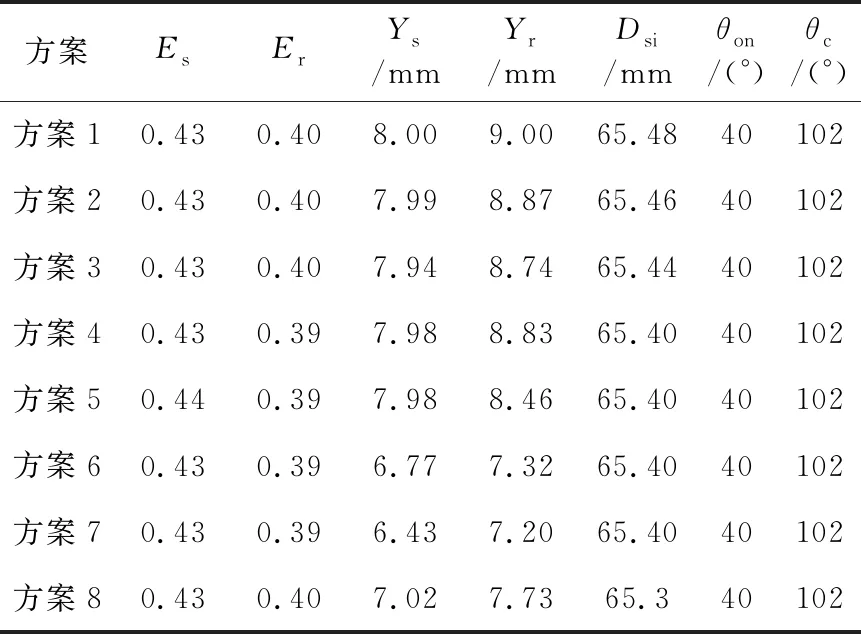
Table 7 SRG optimization schemes based on NSGA-Ⅲ and fuzzy logic NSGA-Ⅲ

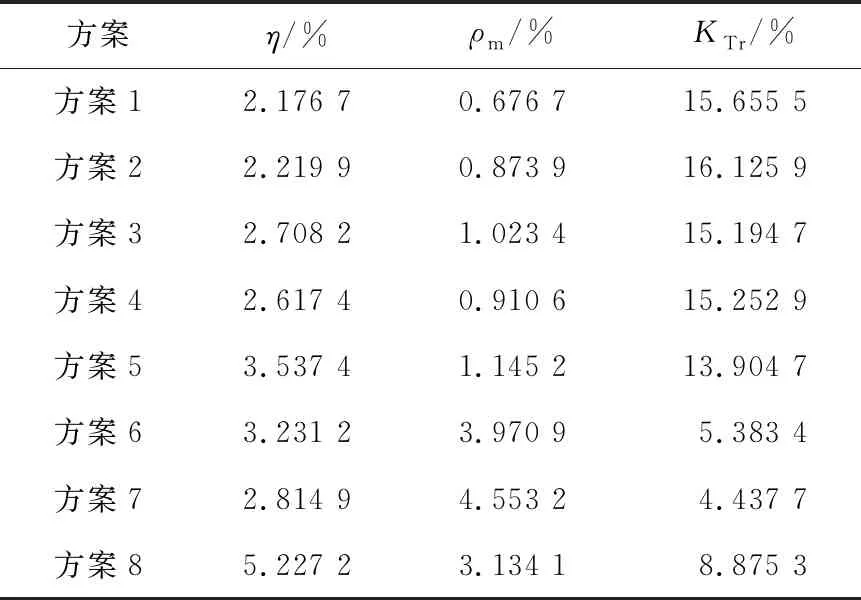
Table 8 Results analysis of SRG optimization schemes

從表9可以看出，方案1～方案5相對于方案8的強度值均為負，即考慮偏好信息時這5組解劣于通過模糊邏輯NSGA-Ⅲ優化得到的相對強度值最大的解。方案6和方案7的相對強度值略大于方案8的，但幅度較小，認為NSGA-Ⅲ優化后的方案6和方案7亦可滿足決策者偏好。NSGA-Ⅲ優化得到的190組Pareto前沿上的解相較于方案8的強度值如圖6所示。

Table 9 Comparison of the relative intensity values of schemes 1～7 and scheme 8

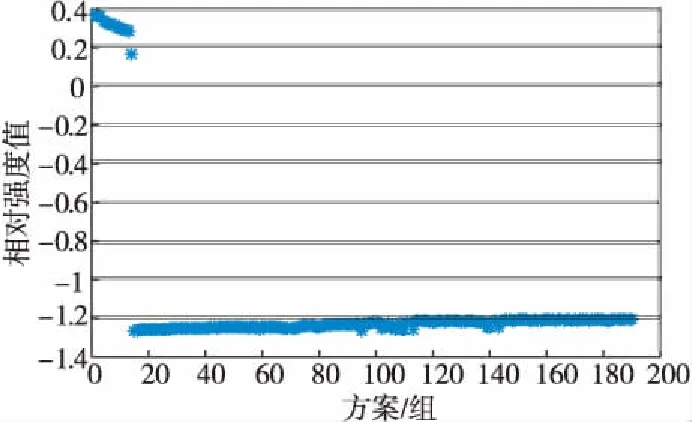
Figure 6 Comparison of the intensity values of the Pareto front of NSGA-Ⅲ and scheme 8

NSGA-Ⅲ優化后Pareto前沿上190組解中有176組解相對于方案8的強度值為負，即考慮偏好的解劣于方案8的。14組解略優于方案8的，均能滿足決策者的偏好需求。由圖6中相對強度值的分布情況可知，NSGA-Ⅲ優化后的Pareto前沿上有可以滿足決策者偏好的解，而模糊邏輯NSGA-Ⅲ相較于NSGA-Ⅲ的優勢在于在算法搜索前設定模糊邏輯，界定了算法的整體尋優方向，更有指向性地實現了全局尋優。

6 結束語

本文進行了基于模糊邏輯NSGA-Ⅲ的SRG多目標優化方法的研究。利用響應面法搭建了SRG非線性模型-回歸模型；采用模糊邏輯NSGA-Ⅲ建立基于模糊邏輯的Mamdani模糊推理系統，通過對優化目標重要性和解改進程度的模糊化，在NSGA-Ⅲ的基礎上引入決策者的偏好信息，以實現Pareto解集相對強度值的量化處理，由相對強度值的大小指導尋優方向；同時，建立適應度函數，以保證種群個體能夠均勻分布到整個搜索域，通過尋優確定SRG的最優參數組合方案。算法采用相對強度值的比較代替了NSGA-Ⅲ中基于關聯操作的非支配排序，使得算法的仿真時長略有增加，但是極大地減小了決策者的決策負擔，縮短了選取最優解的時間。通過有限元仿真對比優化前后SRG的運行性能，強度值最大的優化方案能在減小SRG轉矩脈動的同時，提高發電機的整體運行效率和功率密度，在滿足決策者偏好的基礎上有效地改善了SRG的運行性能，驗證了基于模糊邏輯NSGA-Ⅲ的SRG多目標優化方法的有效性。