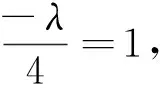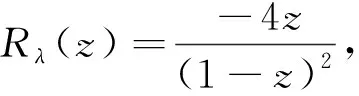Julia集“爆炸”的一族二次有理函數的參數空間
孫 霞
(云南開放大學 公共教學部,云南 昆明 650500)
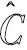
早在1918年,Lattès就找到了一個Julia集為整個Riemann球面的有理函數,即
利用Weierstrass橢圓函數的性質對此進行了證明,但deg(P)=4.在本文中,筆者找到了一族度為2的有理函數,其Julia集也是整個Riemann球面,由于該函數族中的函數與Lattès發現的函數不共軛,所以它們是新的Julia集為整個Riemann球面的有理函數,此外,熟知的有理函數
的Julia集也是整個Riemann球面,但它和我們函數族中的一個函數是共軛的,所以在函數族中.
若2個有理函數是共形共軛的,則它們就具有相同的動力學性質,從而在二次多項式的研究中,只需要研究如下的多項式即可:
Pc(z)=z2+c.
上述含有單參數的多項式族是一個動力學性質比較豐富的函數族,但由于∞是其超吸性不動點,所以它的Fatou集不會是空集,即Julia集不會是整個Riemann球面,也即不會出現Julia集“爆炸”的情況.而對同樣的含有單參數的二次有理函數族
找到了使得其Julia集“爆炸”的具體參數值,并發現這些參數值構成的集合是一個無窮集,結論如下:
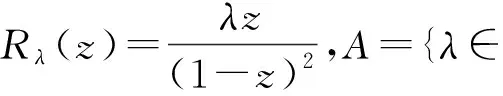
1 預備知識和引理
1.1 不動點及其分類
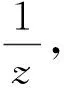
1)稱z為R的超吸引不動點,如果λ=0;
2)稱z為R的吸引不動點,如果|λ|<1;
3)稱z為R的排斥不動點,如果|λ|>1;
4)稱z為R的中性不動點,如果|λ|=1,進一步,若λ=e2πiθ且θ為有理數,則稱z為有理中性不動點;若θ為無理數,則稱z為無理中性不動點.無理中性不動點可以在Fatou集F(R)中,也可以在Julia集J(R)中.若無理中性不動點z∈F(R),則稱z為Siegel點;若z∈J(R),則稱z為Cremer點.
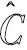
引理2[8-10]有理函數R的吸引和超吸引周期點屬于F(R),排斥周期點屬于J(R).
1.2臨界點
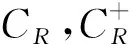
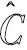
1.3 Sullivan定理
在介紹Sullivan定理之前,先介紹如下定義:
設R為次數不小于2的有理函數,D是Fatou集F(R)的一個分支,則稱D是
1)周期的,如果存在某個正整數n,使得Rn(D)=D;
2)預周期的,如果存在某個正整數m,使得Rm(D)是周期的;
3)游蕩的,如果集合{Rn(D),n≥0}是兩兩互不相交的.
早在上個世紀初,Fatou就猜想,對有理函數來說,不存在游蕩的Fatou分支,這個猜想直到Sullivan引進了有理函數的擬共形形變才獲得證明,結論如下:
引理4[8-10](Sullivan定理) Fatou集的每一個分支都是預周期的.
1.4 Sullivan分類定理
引理5[8-10]設R是有理函數,deg(R)≥2,如果D是R的不變Fatou分支(即R(D)=D),那么,D為下列5種情形之一.
1)吸引的:存在R的吸引不動點z0∈D,其乘子λ滿足0<|λ|<1,Rn在D內局部一致收斂于z0;
2)拋物的:存在R的有理中性不動點z0∈?D,乘子λ=e2πiθ且θ為有理數,Rn在D內局部一致收斂于z0;
3)超吸引的:存在R的超吸引不動點z0∈D,乘子λ=0,Rn在D內局部一致收斂于z0;
4)Siegel盤:D共形等價于單位圓盤Δ,而R共形共軛于Δ上的無理旋轉z|→e2πiθ,z∈Δ,θ為無理數;
5)Hermann環:D共形等價于環域A(r,1)={z|0 引理6[8-10]設R為度deg(R)≥2的有理函數,則R的每個吸引(超吸引)循環的直接吸性域中至少含有R的一個臨界點. 引理7[8-10]設R為deg(R)≥2的有理函數,則R的每個拋物循環的直接吸性域中至少含有R的一個臨界點. …… λ+4=0. (1) 4λ2+(λ+4)2=0. (2) 4λ3(λ+4)2+((λ+4)2+4λ2)2=0. (3) 從上述證明中不難發現,Α?{λ||λ|≥1}.因為0為Rλ的其中一個不動點,若0<|λ|<1,則0是Rλ的吸引不動點,由Sullivan分類定理,存在包含原點的Fatou分支D,此時Julia集不會是整個Riemann球面;若|λ|=1且λ為有理數,則0為有理中性不動點,此時也存在Fatou分支D,使得0∈?D,Julia集也不會是整個Riemann球面;若|λ|=1且λ為無理數,則0可以是Siegel點也可以是Cremer點,此時只有0是Cremer點時Julia集才會是整個Riemann球面.但對集合A的具體狀況不得而知,猜測A可能有內點或者有有限的聚點.1.5 穩定域與臨界點之間的關系
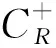
1.6 Julia集為整個Riemann球面的充分條件
1.7 代數學基本定理
2 定理的證明